26. Найдите эксцентриситет гиперболы .
27. Найдите уравнение оси симметрии параболы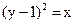 
.
Тест АГ-1. Вариант 5
1. Найдите все простые числа из промежутка [1500, 1510].
2. Вычислите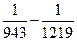 
и запишите результат в виде несократимой дроби.
3. Найдите наименьший по абсолютной величине вычет числа 2345 по модулю 17.
4. Найдите все делители нуля в кольце классов вычетов по модулю 4.
5. Найдите комплексное число, комплексно сопряженное комплексному числу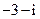 
.
6. Решите уравнение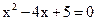 
.
7. По данному вектору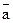 
постройте противоположный ему вектор.
8. Найдите декартовую координату вектора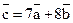 
, если векторы 
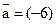и 
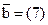коллинеарные оси Ох.
9. Отложите от точки А(–2; –3) вектор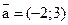 
и найдите координаты его конца.
10. Вектор 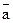имеет направляющие углы 
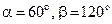,. Вычислите его направляющий угол 
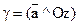, если известно, что он является тупым.
11. Найдите ГЦТ системы из трех материальных точек А(2; 12; 10), В(1; 4; 1), С(1; 2; 3),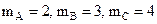 
.
12. На плоскости дан квадрат со стороной 1 и полярная система координат, в которой полюсом служит центр квадрата, а полярный луч проходит через середину его стороны. Найдите полярные координаты вершин квадрата.
13. Постройте на комплексной плоскости комплексное число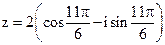 
, найдите его модуль, аргумент, и запишите его в тригонометрической форме.
14. Разложите степенной двучлен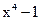 
на линейные множители.
15. Пусть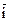 
и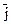 
– орты координатных осей ПДСК Оху. Не пользуясь координатной формой записи, вычислите 
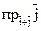. Постройте чертеж.
16. Векторы 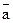и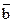 
ортогональны. Зная, что 
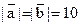, вычислить: а) 
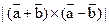; б)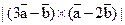 
.
17. Вычислите смешанное произведение векторов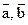 
и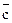 
, если 
.
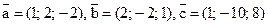18. Найти каноническое и параметрическое уравнения прямой, проходящей через точку А(–1; 2), и параллельной вектору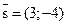 
.
19. Найдите невязку точки М(–2; 9) относительно прямой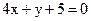 
.
20. Из пучка прямых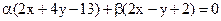 
выберите прямую, проходящую через точку А(1; 3).
21. Составьте уравнение плоскости, проходящей через точку М(2; 1; –1), и перпендикулярной вектору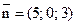 
.
22. Дана плоскость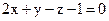 
. Найти отклонение от неё точки А(1; 2; –3).
23. Найти параметрическое уравнение прямой, если её каноническое уравнение имеет вид: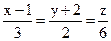 
.
24. Составить уравнения прямой, проходящей через точку
М(2; 0; –3), и перпендикулярной плоскости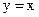 
.
25. Определите взаимное расположение точки М(4, –2) и эллипса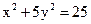 
.