2. С помощью алгоритма Евклида найдите НОД и НОК чисел 1533 и 903.
3. Найдите наименьший неотрицательный вычет числа 1234 по модулю 11.
4. Для каждого класса вычетов по модулю 4 найдите противоположный ему класс вычетов.
5. Найдите алгебраическую форму записи произведения комплексных чисел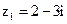 
и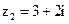 
.
6. Найдите комплексные корни уравнения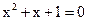 
.
7. Изобразите два произвольных вектора, отложенных от одной точки, и постройте их разность.
8. Найдите декартовую координату вектора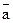 
, коллинеарного оси Ох, если он имеет на этой оси левую ориентацию и его модуль равен 11. Запишите этот вектор в координатной форме записи.
9. Найдите декартовые координаты радиус-вектора точки А(2; 5) и изобразите его на координатной плоскости.
10. Найдите модуль и направляющие косинусы вектора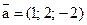 
.
11. Даны концы А(1; –4; 5) и В(–4; 0; 7) однородного стержня. Определить координаты его центра тяжести.
12. Зная декартовые координаты точки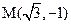 
, найдите её полярные координаты и укажите их на координатной плоскости.
13. Постройте на комплексной плоскости комплексное число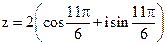 
, найдите его модуль, аргумент, и запишите его в алгебраической форме.
14. Разложите на линейные множители многочлен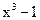 
.
15. Пусть BD – высота правильного треугольника АВС со стороной, равной 1. Найдите скалярное произведение вектора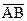 
на вектор 
.
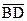16. Дан квадрат ABCD со стороной 1. Изобразите на чертеже данный квадрат и векторное произведение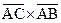 
, отложив его от точки А, вычислите его модуль.
17. Вычислите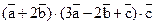 
, если известно, что 
.
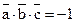18. Найти уравнение прямой с угловым коэффициентом, если её угловой коэффициент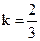 
и известно, что прямая проходит через точку С(0; –1).
19. Найдите расстояние от начала координат до прямой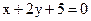 
.
20. Напишите уравнение пучка прямых на координатной плоскости Оху, проходящих через начало координат.
21. Найдите общее уравнение плоскости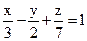 
с целыми коэффициентами, и её нормальный вектор.
22. Дана плоскость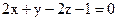 
. Найти для неё невязку точки А(1; 2; –3) .
23. Найти каноническое уравнение прямой, если её параметрическое уравнение имеет вид: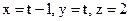 
.
24. Найдите точку пересечения координатной оси абсцисс с плоскостью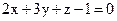 
.
25. Напишите каноническое уравнение эллипса, если его большая ось равна 4, а малая ось равна 2.