6. Построим график функции
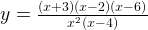
Это дробно-рациональная функция.
Область определения функции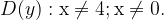 
Нули функции: точки — 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: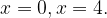 
Если x стремится к бесконечности, то у стремится к 1. Значит,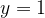 
— горизонтальная асимптота.
Вот эскиз графика:
Еще один интересный прием — сложение графиков.
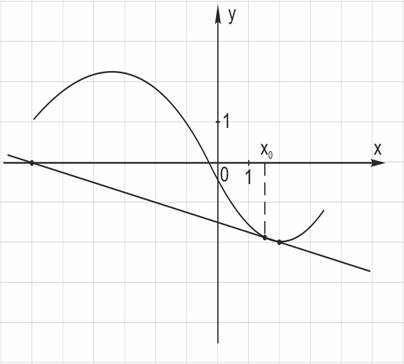
7. Построим график функции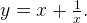 
Если x стремится к бесконечности, то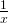 
и график функции будет бесконечно близко подходить к наклонной асимптоте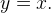 
Если x стремится к нулю, то функция ведет себя как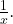 
Это мы и видим на графике:
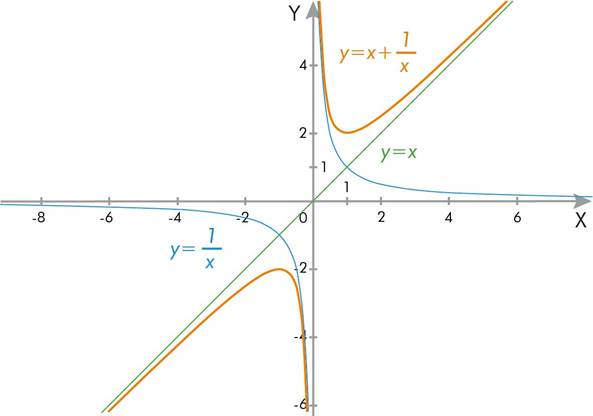
Вот мы и построили график суммы функций. Теперь график произведения!
8. Построим график функции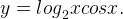 
Область определения этой функции — положительные числа, поскольку только для положительных x определен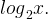 
Значения функции равны нулю при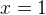 
(когда логарифм равен нулю), а также в точках, где 
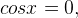то есть при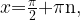 
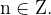
При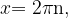 
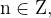значение cos x равно единице. Значение функции в этих точках будет равно 
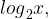при 
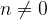
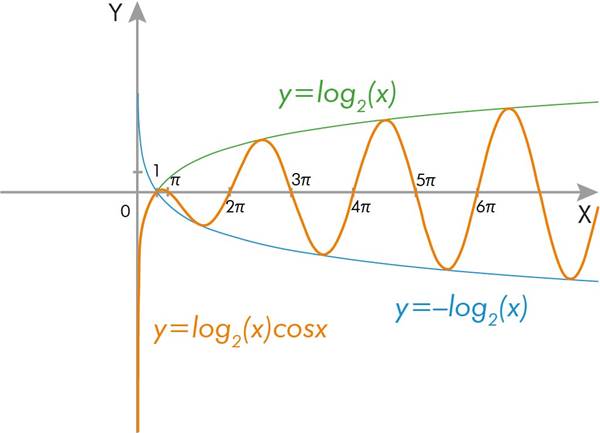
9. Построим график функции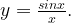 
Функция определена при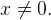 
Она четная, поскольку является произведением двух нечетных функци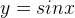й 
и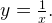 
График симметричен относительно оси ординат.
Нули функции — в точках, где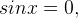 
то есть 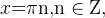при 
при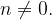 
Если x стремится к бесконечности,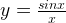 
стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное 
?
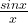Оказывается, что если x стремится к нулю, то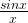 
стремится к единице. В математике это утверждение носит название «Первого замечательного предела».
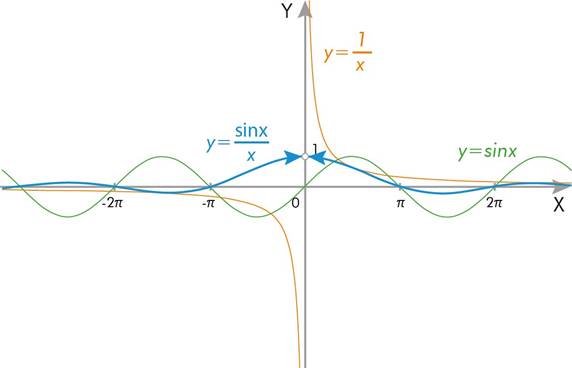
А как же производная? Да, наконец-то мы до нее добрались. Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.
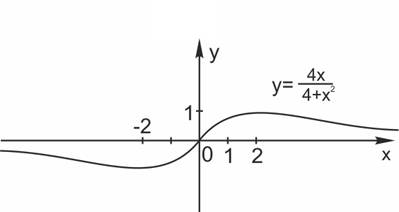
10. Построим график функции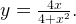 
Область определения функции — все действительные числа, поскольку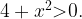 
Функция нечетна. Ее график симметричен относительно начала координат.
При x=0 значение функции равно нулю. При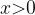 
значения функции положительны, при 
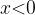отрицательны.
Если x стремится к бесконечности, то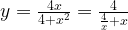 
стремится к нулю.
Найдем производную функции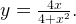
По формуле производной частного,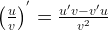 
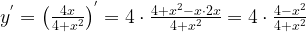
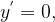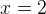если 
или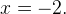 
В точке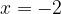 
производная меняет знак с «минуса» на «плюс», 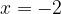— точка минимума функции.
В точке 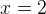производная меняет знак с «плюса» на «минус», 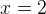— точка максимума функции.
Найдем значения функции при x=2 и при x=-2.
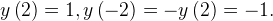
Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?
Общая схема построения графика функции:
1. Область определения функции