Как вывести формулу обратной функции?
Если вы учитесь в математическом классе или на первом курсе вуза, вам может встретиться такое задание.
Например, у вас есть линейная функция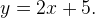 
Какая же функция будет к ней обратной?
Действуем следующим образом:
1) Выражаем из формулы функции x через у.
Получаем: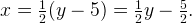 
2) В формуле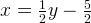 
меняем x и у местами. Получаем формулу обратной функции: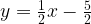 
Другой пример. Найдем обратную функцию для функции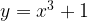 
.
1) Выражаем из формулы функции x через у. Получаем: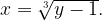 
2) В формуле 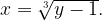меняем x и у местами. Получаем формулу обратной функции: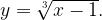 
Понятие функции — одно из ключевых в математике. О нём подробно рассказано в статье «Что такое функция».
И конечно, в задачах части 2 Профильного ЕГЭ по математике без них не обойтись. А если вы выбрали технический или экономический вуз — первая же лекция по матанализу будет посвящена именно элементарным функциями и их графикам.
Но это не всё. Математические функции, изучением которых мы занимаемся, — это не что-то такое выдуманное или существующее только в замкнутом пространстве учебника. Они являются отражением реальных взаимосвязей и процессов, происходящих в природе и обществе.
Существует всего пять типов элементарных функций:
1. Степенные
К этому типу относятся линейные, квадратичные, кубические,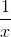 
, 
, 
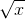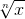Все они содержат выражения вида xα.
2. Показательные
Это функции вида y = ax
3. Логарифмические
y = logax.
4. Тригонометрические
В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы.
5. Обратные тригонометрические
Содержат arcsinx, arccosx, arctgx, arcctgx.
Элементарными они называются потому, что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x2 · ex — произведение квадратичной и показательной функций; y = sin(ax) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.
Графики и свойства основных элементарных функций следует знать наизусть.
Степенные функции
| 1. Линейная функция y = x |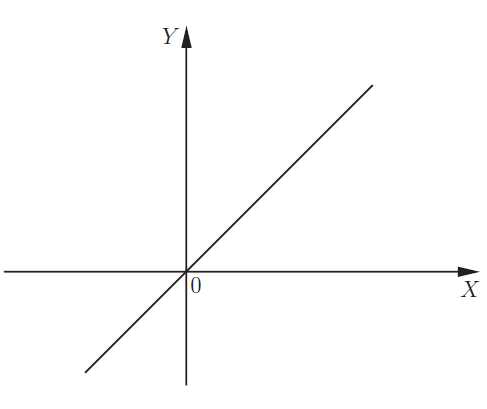 
|
| 2. Квадратичная парабола y = x2 |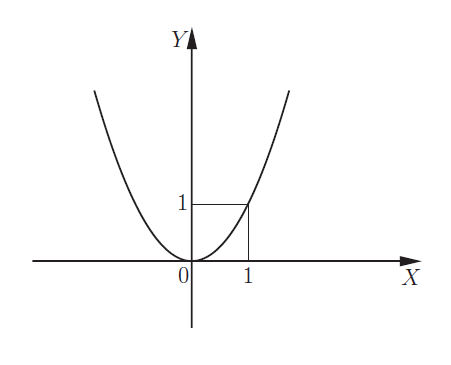 
|
| 3. Функция y = xn, n - натуральное, n > 1 n - чётное n = 2, 4, 6,... |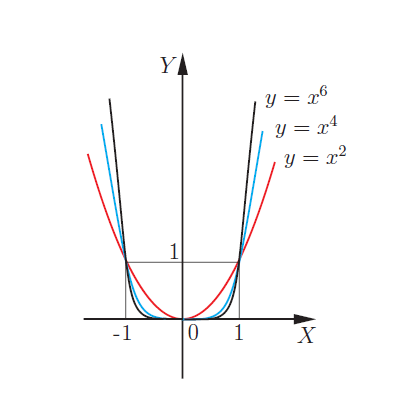 
|
| n - нечётное n = 3, 5, 7,... |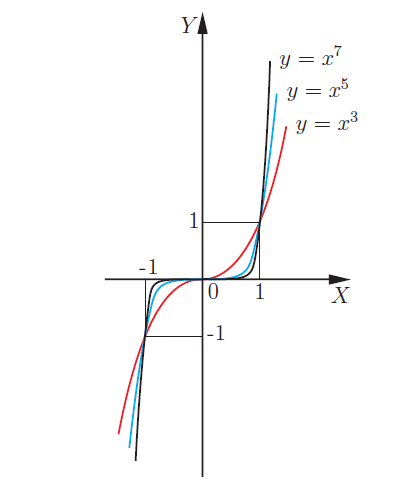 
|
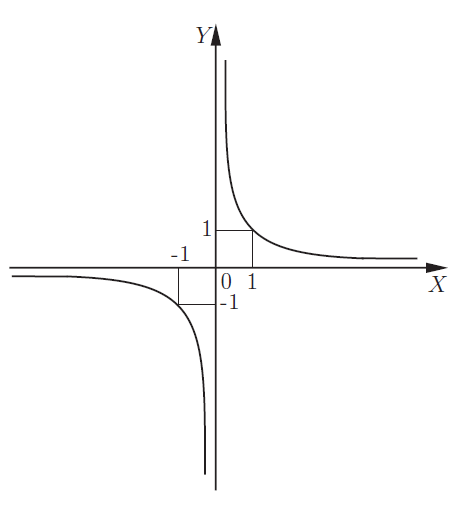
4.Гипербола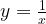 
| 
|
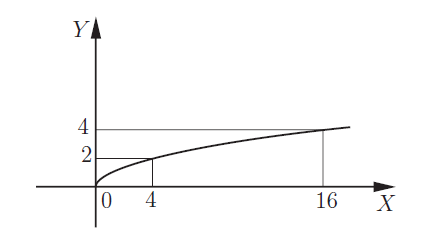
5. 
| 
|
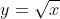
6. 
| 
|
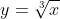
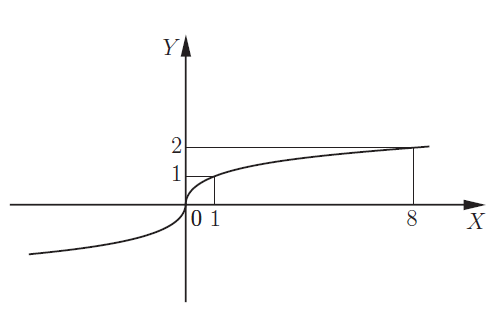
Показательная функция y = a x
| a > 1 |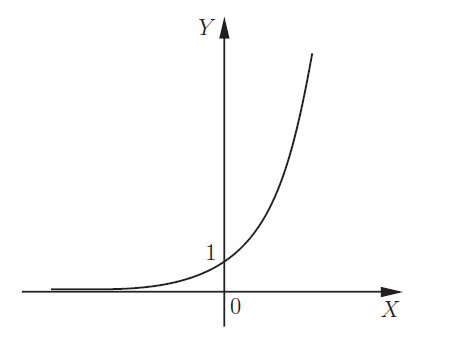 
|
| 0 < a < 1 |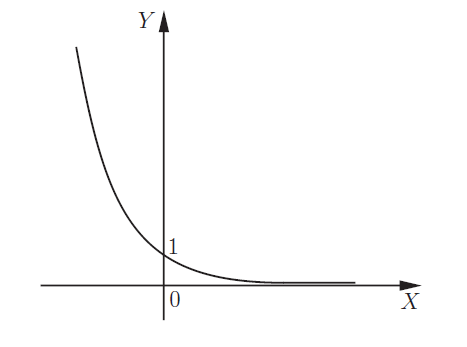 
|
Логарифмическая функция y = log a x
| a > 1 |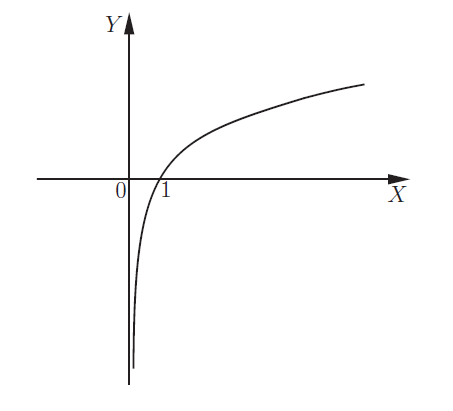 
|
| 0 < a < 1 |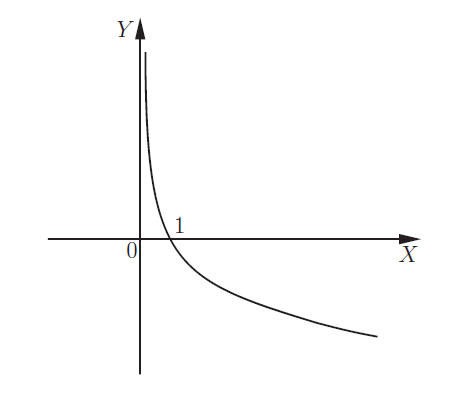 
|