Перечислим способы задания функции.

Дата: 2025-06-02; Просмотры: 22
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

1. С помощью формулы. Это удобный и привычный для нас способ. Например:

,

,

,

.

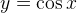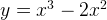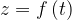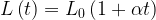Это примеры функций, заданных формулами.

2. Графический способ. Он является самым наглядным. На графике сразу видно все – возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума. В следующей статье будет рассказано об исследовании функции с помощью графика.

К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.

3. С помощью таблицы. С этого способа вы когда-то начинали изучение темы «Функция» - строили таблицу и только после этого – график. А при экспериментальном исследовании какой-либо новой закономерности, когда еще неизвестны ни формула, ни график, этот способ будет единственно возможным.

4. С помощью описания. Бывает, что на разных участках функция задается разными формулами. Известная вам функция 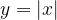задается описанием:

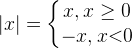
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:

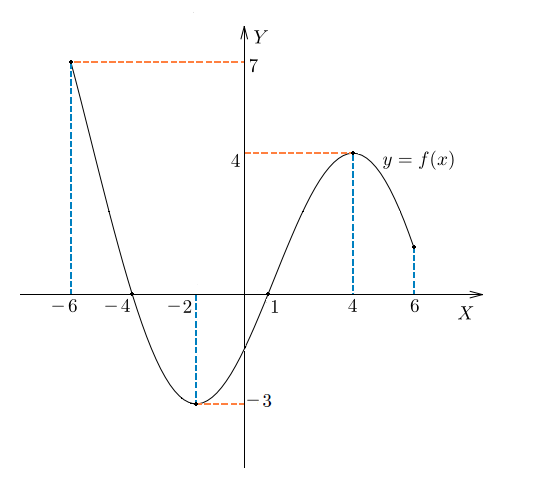
Уточним терминологию:

Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .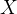
Ось ординат — вертикальная ось, или ось .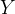

Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .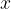
Другими словами, мы сами выбираем 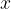, подставляем в формулу функции и получаем .

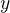Область определения функции — множество тех (и только тех) значений аргумента 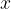, при которых функция существует.
Обозначается: 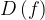или .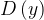

На нашем рисунке область определения функции 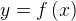— это отрезок 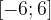. Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.

Область значений функции — это множество значений, которые принимает переменная 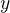. На нашем рисунке это отрезок 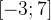— от самого нижнего до самого верхнего значения .

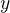Нули функции — точки, где значение функции равно нулю, то есть 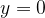. На нашем рисунке это точк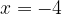и и 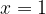.