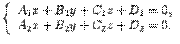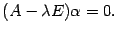C войства обратных матриц
кажем следующие свойства обратных матриц:
1) (A-1)-1 = A;
2) (AB)-1 = B-1A-1
3) (AT)-1 = (A-1)T.
10) Линейная зависимость
Линейная зависимость (матем.), соотношение вида
C11u1 + C2u2 + ... + Cnun = 0, (*)
где С1, C2, ..., Cn — числа, из которых хотя бы одно отлично от нуля, а u1, u2, ..., un — те или иные матем. объекты, для которых определены операции сложения и умножения на число. В соотношение (*) объекты u1, u2, ..., un входят в 1-й степени, т. е. линейно; поэтому описываемая этим соотношением зависимость между ними называется линейной. Знак равенства в формуле (*) может иметь различный смысл и в каждом конкретном случае должен быть разъяснён. Понятие Л. з. употребляется во многих разделах математики. Так, можно говорить о Л. з. между векторами, между функциями от одного или нескольких переменных, между элементами линейного пространства и т. д. Если между объектами u1, u2, ..., un имеется Л. з., то говорят, что эти объекты линейно зависимы; в противном случае их называется линейно независимыми. Если объекты u1, u2, ..., un линейно зависимы, то хотя бы один из них является линейной комбинацией остальных, т. е.
u1 = a 1u1 + ... + a i-1ui-1 + a i+1ui+1 + ... + a nun.
Непрерывные функции от одного переменного
u1 = j 1(х), u2 = j 2(х), ..., un = j n(x) называются линейно зависимыми, если между ними имеется соотношение вида (*), в котором знак равенства понимается как тождество относительно х. Для того чтобы функции j 1(x), j2(x), ..., j n(x), заданные на некотором отрезке а £ х £ b, были линейно зависимы, необходимо и достаточно, чтобы обращался в нуль их определитель Грама
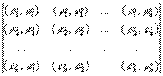
где
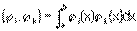
i, k = 1,2, ..., n.
Если же функции j1 (x), j2(x), ..., jn(x) являются решениями линейного дифференциального уравнения, то для существования Л. з. между ними необходимо и достаточно, чтобы вронскиан обращался в нуль хотя бы в одной точке.
Линейные формы от m переменных
u1 = ai1x1 + ai2x2 + ... + aimxm
(i = 1, 2, ..., n)
называются линейно зависимыми, если существует соотношение вида (*), в котором знак равенства понимается как тождество относительно всех переменных x1, x2, ..., xm. Для того чтобы n линейных форм от n переменных были линейно зависимы, необходимо и достаточно, чтобы обращался в нуль определитель
D= 
Свойство 1. Если среди векторов 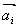 есть нулевой вектор, то эти векторы линейно зависимы.
есть нулевой вектор, то эти векторы линейно зависимы.
Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Свойство 6. Любые 4 вектора линейно зависимы.
Пусть V будет линейное пространство над полем K и 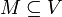 . M называется линейно независимым множеством, если любое его конечное подмножество является линейно независимым.
. M называется линейно независимым множеством, если любое его конечное подмножество является линейно независимым.
Конечное множество M' = {v1,v2,...,vn} называется линейно независимым, если единственная линейная комбинация, равная нулю, тривиальна, то есть состоит из факторов, равных нулю:

Если существует такая линейная комбинация с минимум одним 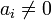 , M' называется линейно зависимым. Обратите внимание, что в первом равенстве подразумевается
, M' называется линейно зависимым. Обратите внимание, что в первом равенстве подразумевается 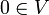 , а во втором
, а во втором 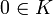 .
.
Свойства
1 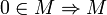 линейно зависимо
линейно зависимо
2 M линейно независимо 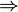 M' линейно независимо для всех
M' линейно независимо для всех 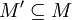
3 M линейно зависимо 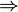 M' линейно зависимо для всех
M' линейно зависимо для всех 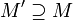
12) Сме́шанное произведе́ние
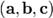 векторов
векторов 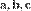 — скалярное произведение вектора
— скалярное произведение вектора 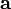 на векторное произведение векторов
на векторное произведение векторов  и
и 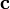 :
:
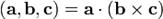 .
.
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами
Свойства
Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
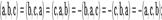
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что 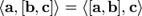
2 Смешанное произведение  в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов
в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов  и
и 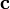 :
:
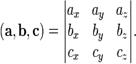
В частности,
3 Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю
4 Геометрический смысл — Смешанное произведение 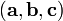 по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами
по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами 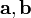 и
и 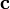 ; знак зависит от того, является ли эта тройка векторов правой или левой
; знак зависит от того, является ли эта тройка векторов правой или левой
§ 5 Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:
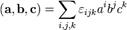
(в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов).

16) рямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.
Итак, если уравнения двух непараллельных плоскостей -- 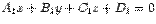 и
и 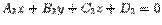 , то прямая, являющаяся их линией пересечения, задается системой уравнений
, то прямая, являющаяся их линией пересечения, задается системой уравнений
|
| (11.11) |
И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.
Уравнения (11.11) называют общими уравнениями прямой в пространстве.
Замечание 11.2 Любые попытки с помощью преобразований уравнений системы (11.11) получить одно (линейное) уравнение, задающее прямую, обречены на неудачу. Одно уравнение -- это уравнение плоскости. Общие уравнения прямой "неудобны" для получения информации о положении прямой.
Например, чтобы найти координаты какой-нибудь точки на прямой, нужно провести довольно сложные вычисления. А именно, задать произвольно какую-нибудь координату, подставить ее в систему (11.11) и из получившейся системы двух уравнений с двумя неизвестными найти две остальные координаты. Причем может оказаться, что полученная система не имеет решений. Тогда нужно произвольно задать другую координату и из системы найти две оставшиеся координаты.
18)НЕРАВЕНСТВО КОШИ-БУНЯКОВСКОГО
Для любых векторов x и y евклидова пространства E со скалярным призведением (x, y) справедливо неравенство:
|(x, y)|2 ≤ (x, x)·(y, y).
20Ортогональный (ортонормированный) базис — ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты.
Ортогональный базис — система попарно ортогональных элементов 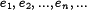 гильбертова пространства
гильбертова пространства 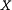 такая, что любой элемент
такая, что любой элемент 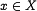 однозначно представим в виде сходящегося по норме ряда
однозначно представим в виде сходящегося по норме ряда
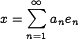
называемым рядом Фурье элемента  по системе
по системе 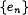 . Обычно базис
. Обычно базис 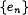 выбирается так, что
выбирается так, что 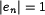 , и тогда он называется ортонормированным базисом. В этом случае числа
, и тогда он называется ортонормированным базисом. В этом случае числа 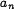 , называются коэффициентами Фурье элемента
, называются коэффициентами Фурье элемента  по ортонормированному базису
по ортонормированному базису 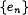 , имеют вид
, имеют вид
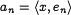 .
.
Необходимым и достаточным условием того, чтобы ортонормированная система 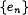 была базисом, является равенство Парсеваля
была базисом, является равенство Парсеваля
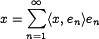
для любого 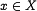 . Гильбертово пространство, имеющее ортонормированный базис, являетсясепарабельным, и обратно, во всяком сепарабельном гильбертовом пространстве существует ортонормированный базис.
. Гильбертово пространство, имеющее ортонормированный базис, являетсясепарабельным, и обратно, во всяком сепарабельном гильбертовом пространстве существует ортонормированный базис.
Если задана произвольная система чисел 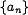 такая, что
такая, что 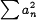 , то в случае гильбертова пространства с ортонормированным базисом
, то в случае гильбертова пространства с ортонормированным базисом 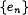 ряд
ряд 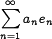 - сходится по норме к некоторому элементу
- сходится по норме к некоторому элементу 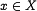 . Этим устанавливается изоморфизм любого сепарабельного гильбертова пространства пространству
. Этим устанавливается изоморфизм любого сепарабельного гильбертова пространства пространству 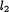 (теорема Рисса — Фишера).
(теорема Рисса — Фишера).
Коэффициенты Фурье функции f периода 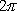
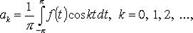
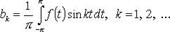
либо
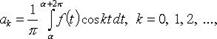
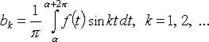
22)Определение собственного числа и собственного вектора квадратной матрицы 
Собственным вектором квадратной матрицы M называется вектор 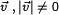 , который удовлетворяет соотношению
, который удовлетворяет соотношению 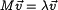 , где
, где 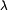 — собственное значение, соответствующее данному собственному вектору. Одному собственному значению может соответствовать несколько (линейно независимых) собственных векторов, в таком случае говорят о собственном подпространстве для данного собственного значения. Собственными векторами линейного преобразования называются собственные вектора матрицы, определяющей это преобразование.
— собственное значение, соответствующее данному собственному вектору. Одному собственному значению может соответствовать несколько (линейно независимых) собственных векторов, в таком случае говорят о собственном подпространстве для данного собственного значения. Собственными векторами линейного преобразования называются собственные вектора матрицы, определяющей это преобразование.
Свойства собственных векторов и значений  Линейная комбинация собственных векторов матрицы
Линейная комбинация собственных векторов матрицы 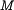 , соответствующих одному и тому же собственному значению
, соответствующих одному и тому же собственному значению 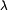 , также является собственным вектором
, также является собственным вектором 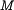 с собственным значением
с собственным значением 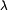 .
.
1Количество различных собственных значений не может превышать размер матрицы.
2Сумма размерностей собственных подпространств, соответствующих всем собственным значениям равна размерности матрицы (в случае рассмотрения комплексных чисел).
3Собственные векторы, самосопряженного оператора А соответствующие различным собственным значениям ортогональны.
Т. е. если 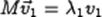 ,
, 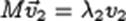 и
и 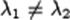 , то
, то 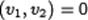
Для произвольной матрицы это не верно.
24) подобные матрицы их собственные числа
Квадратные матрицы A и B одинакового порядка называются подобными, если существует невырожденная матрица P того же порядка, такая что: 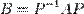
Подобные матрицы получаются при задании матрицей линейного преобразования в разных координатных системах; при этом матрица Р является матрицей перехода от одной системы к другой.
Свойства
Отношение подобности матриц является отношением эквивалентности в пространстве квадратных матриц.
У подобных матриц совпадают многие характеристики, а именно:
§ ранг
§ определитель
§ след
§ собственные значения (но собственные векторы могут не совпадать)
§ характеристический многочлен
§ Жорданова форма с точностью до перестановки клеток
Можно доказать, что любая матрица A подобна AT.
Собственными числами матрицы 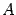 являются корни уравнения
являются корни уравнения
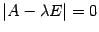
и только они.
Доказательство. Пусть столбец 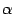 -- собственный вектор матрицы
-- собственный вектор матрицы  с собственным числом
с собственным числом 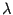 . Тогда, по определению,
. Тогда, по определению, 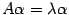 . Это равенство можно переписать в виде
. Это равенство можно переписать в виде 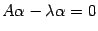 . Так как для единичной матрицы
. Так как для единичной матрицы 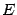 выполнено
выполнено 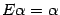 , то
, то 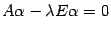 . По свойству матричного умножения
. По свойству матричного умножения 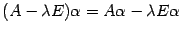 и предыдущее равенство принимает вид
и предыдущее равенство принимает вид
|
| (19.4) |
Допустим, что определитель матрицы 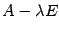 отличен от нуля,
отличен от нуля, 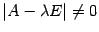 . Тогда у этой матрицы существует обратная
. Тогда у этой матрицы существует обратная 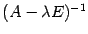 . Из равенства (19.4) получим, что
. Из равенства (19.4) получим, что 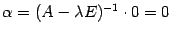 , что противоречит определению собственного вектора. Значит, предположение, что
, что противоречит определению собственного вектора. Значит, предположение, что 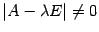 , неверно, то есть все собственные числа должны являться корнями уравнения
, неверно, то есть все собственные числа должны являться корнями уравнения 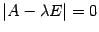 .
.
Пусть 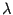 -- корень уравнения
-- корень уравнения 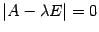 . Тогда базисный минор матрицы
. Тогда базисный минор матрицы 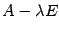 не может совпадать с определителем матрицы и поэтому
не может совпадать с определителем матрицы и поэтому 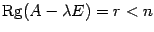 ,
, 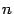 -- порядок матрицы
-- порядок матрицы 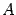 . Уравнение (19.4) является матричной записью однородной системы линейных уравнений с неизвестными
. Уравнение (19.4) является матричной записью однородной системы линейных уравнений с неизвестными 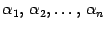 , являющимися элементами матрицы-столбца
, являющимися элементами матрицы-столбца 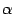 . По теореме 15.3 число решений в фундаментальной системе решений равно
. По теореме 15.3 число решений в фундаментальной системе решений равно 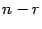 , что больше нуля. Таким образом, система (19.4) имеет хотя бы одно ненулевое решение, то есть числу
, что больше нуля. Таким образом, система (19.4) имеет хотя бы одно ненулевое решение, то есть числу 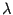 соответствует хотя бы один собственный вектор матрицы
соответствует хотя бы один собственный вектор матрицы 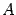 .
.
Определитель 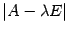 является многочленом степени
является многочленом степени 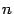 от переменного
от переменного 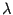 , так как при вычислении определителя никаких арифметических действий кроме сложения, вычитания и умножения выполнять не приходится.
, так как при вычислении определителя никаких арифметических действий кроме сложения, вычитания и умножения выполнять не приходится.
26) Квадратичной формой называется функция B(x) = A(x,x) из линейного пространства L над произвольным полем F характеристики не 2 в поле F, которая получается избилинейной формы A(x,y) при x = y.
При фиксированном базисе 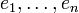 в L квадратичная форма имеет вид
в L квадратичная форма имеет вид
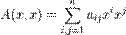
где 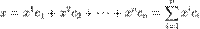 , а aij = aji.
, а aij = aji.
Матрицу (aij) называют матрицей квадратичной формы в данном базисе.
Свойства
§ Симметричную билинейную форму A(x,y), называют полярной квадратичной форме A(x,x). Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.
§ Если матрица квадратичной формы имеет полный ранг, то квадратичную форму называют невырожденной, иначе — вырожденной.
§ Квадратичная форма A(x,x) называется положительно (отрицательно) определённой, если для любого 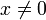
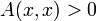
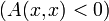 . Положительно определённые и отрицательно определённые формы называются знакоопределёнными.
. Положительно определённые и отрицательно определённые формы называются знакоопределёнными.
§ Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
§ Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
§ Квадратичная форма A(x,x) называется знакопеременной, если она принимает как положительные, так и отрицательные значения.
§ Квадратичная форма A(x,x) называется квазизнакоопределённой (полуопределенной), если 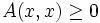
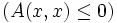 , но форма не является знакоопределённой.
, но форма не является знакоопределённой.
Для определения того, к какому из этих трёх типов относится квадратичная форма, можно воспользоваться критерием Сильвестра.
§ Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.
§ Для любой квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид: A(x,x) = λi(xi)2. Для приведения квадратичной формы к каноническому виду используется метод Лагранжа.
Приведение квадратичных форм к каноническому виду
§ Рассмотрим некоторое линейное преобразование А с матрицей 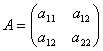 .
.
§ Это симметрическое преобразование можно записать в виде:
§ y1 = a11x1 + a12x2
§ y2 = a12x1 + a22x2
§ где у1 и у2 – координаты вектора 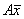 в базисе
в базисе 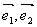 .
.
§ Очевидно, что квадратичная форма может быть записана в виде
§ Ф(х1, х2) = х1у1 + х2у2.
§
§ Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х1 и х2 – скалярное произведение 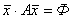 .
.
§ Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.
§ Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:
§ 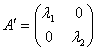
классификация квадратичных форм
§ Определение . Квадратичной формой 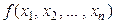 от n неизвестных называется многочлен от n переменных второй степени, не содержащий членов первой степени и свободного члена
от n неизвестных называется многочлен от n переменных второй степени, не содержащий членов первой степени и свободного члена
§ 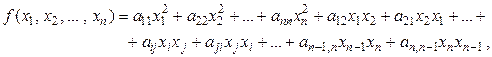
§ причем 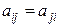 "
" 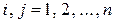 (
( 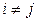 ).
).
§ Замечание . С учетом условия 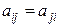 "
" 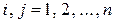 (
( 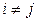 ) квадратичную форму обычно записывают в виде:
) квадратичную форму обычно записывают в виде:
§ 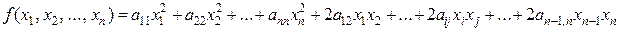 .
.
§ Из коэффициентов 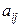 можно составить квадратную матрицу n-го порядка
можно составить квадратную матрицу n-го порядка
§ 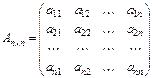 ,
,
§ которая называется матрицей квадратичной формы f, а ее ранг r называется рангом квадратичной формы f.
§ Если 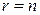 , т.е. матрица A невырождена (
, т.е. матрица A невырождена ( 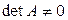 ), то и квадратичная форма f называется невырожденной.
), то и квадратичная форма f называется невырожденной.
§ Из условия 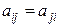 "
" 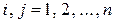 (
( 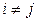 ) следует, что
) следует, что 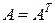 , т.е. матрица A – симметрическая.
, т.е. матрица A – симметрическая.
§ Обратно, для любой симметрической матрицы A n-го порядка можно указать вполне определенную квадратичную форму f от n неизвестных, имеющую элементы матрицы A своими коэффициентами.
§ Пример 1. Составить матрицу A квадратичной формы от трех неизвестных
.27)гипербола
Гипербола
Гиперболой называется геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называеых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению и обозначается через2а. Фокусы гиперболы обозначают буквами 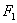 и
и 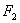 , расстояние между ними - через 2с. По определению гиперболы
, расстояние между ними - через 2с. По определению гиперболы 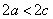 , или
, или 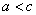 .
.
Пусть дана гипербола. Если оси декатовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид
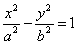 (1)
(1)
где 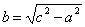 . Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат - ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии - центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. Вершины гиперболы суть точки А’ и А.
. Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат - ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии - центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. Вершины гиперболы суть точки А’ и А.
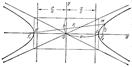
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.
Отрезки длиной 2a и 2b, соединяющие середины сторон основного прямоугольника гиперболы, также называют ее осями. Диагонали основного прямоугольника (неограниченно продолженного) являются асимптотами гиперболы, их уравнения суть
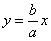 ,
, 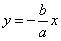
Уравнение
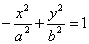 (2)
(2)
определяет гиперболу, симметричную относительно координатных осей, с фокусами на оси ординат; уравнение (2), как и уравнение (1), называется каноническим уравнением гиперболы; в этом случае постоянная разность расстояний от произвольной точки гиперболы до фокусов равна 2b.
Две гиперболы, которые определяются уравнениями
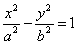 ,
, 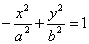
в одной и той же системе координат, называются сопряженными.
Гипербола с равными полуосями (a=b) называется равносторонней; ее каноническое уравнение имеет вид
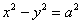 или
или 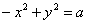
Число
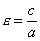
где а - расстояние от центра гиперболы до ее вершины, называется эксцентриситетом гиперболы. Очевидно, для любой гиперболы 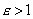 . Если М(x; y) - произвольная точка гиперболы, то отрезки
. Если М(x; y) - произвольная точка гиперболы, то отрезки 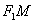 и
и 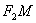 (см. рис.) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам
(см. рис.) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам
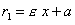 ,
, 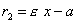 ,
,
фокальные радиусы точек левой ветви - по формулам
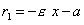 ,
, 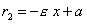 .
.
Если гипербола задана уравнением (1), то прямые, определяемые уравнениями
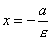 ,
, 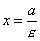 ,
,
называются ее директрисами (см. рис.). Если гипербола задана уравнением (2), то директрисы определяются уравнениями
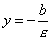 ,
, 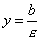 .
.
Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки гиперболы до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентрисистету гиперболы:
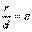 .
.
Каноническое сечение


Три основных конических сечения
Гипербола может быть определена, как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как скрещенные и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, скрещенные прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.
становим форму эллипса, пользуясь его каноническим уравнением.
1. Уравнение (11.7) содержит х и у только в четных степенях, поэтому если точка 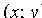 принадлежит эллипсу, то ему также принадлежат точки
принадлежит эллипсу, то ему также принадлежат точки 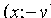 ,
, 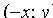 ,
, 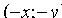 . Отсюда следует, что эллипс симметричен относительно осей
. Отсюда следует, что эллипс симметричен относительно осей  и
и  , а также относительно точки
, а также относительно точки  , которую
, которую 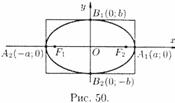 называют центром эллипса.
называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат. Положив 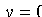 , находим две точки
, находим две точки 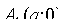 и
и 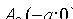 , в которых ось
, в которых ось 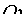 пересекает эллипс (см. рис. 50). Положив в уравнении (11.7)
пересекает эллипс (см. рис. 50). Положив в уравнении (11.7) 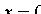 , находим точки пересечения эллипса с осью
, находим точки пересечения эллипса с осью 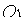 :
: 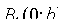 и
и 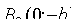 . Точки A1, A2 , B1, B2 называются вершинами эллипса . Отрезки A1A2 и B1B2, а также их длины 2a и 2bназываются соответственно большой и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.
. Точки A1, A2 , B1, B2 называются вершинами эллипса . Отрезки A1A2 и B1B2, а также их длины 2a и 2bназываются соответственно большой и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.
3. Из уравнения (11.7) следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства 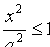 и
и 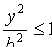 или
или 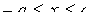 и
и 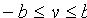 . Следовательно, все точки эллипса .лежаї внутри прямоугольника, образованного прямыми
. Следовательно, все точки эллипса .лежаї внутри прямоугольника, образованного прямыми 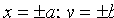 .
.
4. В уравнении (11.7) сумма неотрицательных слагаемых 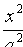 и
и 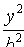 равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если
равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если 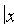 возрастает, то
возрастает, то 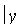 уменьшается и наоборот.
уменьшается и наоборот.
30)цилиндрические поверхности
Цилиндрические поверхности
Определение. Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой- либо фиксированной прямой.
Рассмотрим поверхности, в уравнении которых отсутствует составляющая z, т.е. направляющие параллельны оси Оz. Тип линии на плоскости ХOY (эта линия называется направляющей поверхности) определяет характер цилиндрической поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения направляющих:
1) 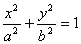 - эллиптический цилиндр.
- эллиптический цилиндр.
2) 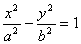 - гиперболический цилиндр.
- гиперболический цилиндр.

2) x2 = 2py – параболический цилиндр.