9 Линейное векторное пространство, аксиомы. Пространства С n и Rn
Лине́йное простра́нство, или ве́кторное простра́нство, является обобщением понятия совокупности всех векторов 3-мерного пространства. Линейные пространства — основной объект изучения линейной алгебры.
I. Имеется правило, посредством которого любым двум элемен-
там x,y множества V ставится в соответствие третий элемент этого
множества., называемый суммой элементов х и у и обозначаемый
символом z = x+y
II. Имеется правило, посредством которого любому элементу х
множества V и любому элементу λ ∈K ставится в соответствие
элемент и этого множества, называемый произведением элемента х
на элемент λ и обозначаемый символом и = λ x .
III. Указанные два правила подчинены следующим восьми акси-
омам :
1. x + y = y + x (коммутативность)
2. (x + y) + z = x + ( y + z) (ассоциативность)
3. Существует нулевой элемент 0 такой, что x + 0 = 0 + x = x (для
любого х)
4. Для каждого элемента х существует противоположный эле-
мент х'∈V такой, что х + х' = 0
5. 1⋅ x = x , где 1 – еденица поля
6. λ ⋅ (μ x) = (λμ ) ⋅ x, λ ,μ ∈K .
7. (λ +μ )x = λ x +μ x, λ ,μ ∈K.
8. λ (x + y) = λ x +λ y, λ ∈K .
11. Размерность пространства. Базис. Разложение вектора по базису
Определение. Вектор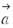 
называется линейной комбинацией векторов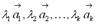 
векторного пространства R, если он равен сумме произведений этих векторов на произвольные действительные числа: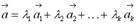 
где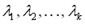 
– какие угодно действительные числа.
Ба́зис — набор n векторов в n-мерном линейном пространстве, таких, что любой вектор пространства может быть представлен в виде некоторой их линейной комбинации, при этом ни один из базисных векторов не представим в виде линейной комбинации остальных.
В более точной формулировке, базис в векторном пространстве — это упорядоченная линейно независимая система векторов такая, что любой вектор этого пространства разложим по ней.
Некоторые свойства базиса :
Единственная тривиальная линейная комбинация векторов базиса возможна только при тривиальном наборе коэффициентов.
Для любого вектора существует единственное представление в виде линейной комбинации соответствующего базиса.
Количество векторов базиса не зависит от выбора базисных векторов и называется размерностью пространства (обозначается dimV).
Представление вектора в виде линейной комбинации базисных векторов называется разложением вектора по данному базису.