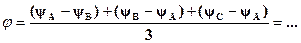8.1. Напряжения в трехфазной цепи
8.1.1. Общие сведения
Трехфазная система напряжений (ЭДС) – это совокупность трех синусоидальных напряжений (ЭДС), сдвинутых относительно друг друга по фазе. Система называется симметричной, если амплитуды всех трех напряжений одинаковы, а фазовые сдвиги составляют 120о.
Обычный трехфазный генератор, применяемый в электроэнергетике, состоит из неподвижного статора и вращающегося ротора. На роторе имеется обмотка возбуждения, по которой протекает постоянный ток от синусоидального источника. Постоянный ток создает магнитное поле, вращающееся вместе с ротором. На статоре имеется три обмотки, смещенные относительно друг друга в пространстве на 120о. В них наводится три одинаковых синусоидальных ЭДС, смещенных во времени. Фазовый сдвиг составляет 120о.
Временная развертка этих напряжений приведена на рис. 8.1.1. Они же представлены в виде векторов на диаграмме (рис. 8.1.2).
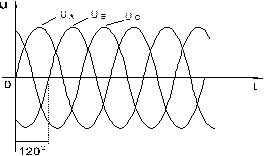
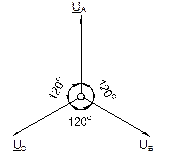
Рис. 8.1.1 Рис. 8.1.2
В трехфазных электрических генераторах и нагрузках (в частности, двигателях) в качестве основных схем соединения фаз используются «звезда» (рис. 8.1.3) и «треугольник» (рис. 8.1.4). Соединение в звезду может выполняться с нейтральным проводом (на рисунке он показан пунктиром) или без него.
В схеме «звезда» напряжения между выводами А, В и С называются линейными, тогда как напряжение между любой из этих точек и нейтралью N принято называть фазным. Векторная диаграмма напряжений такой трехфазной цепи приведена также на рис. 8.1.3, где показаны соотношения между фазами и величинами линейных UЛ и фазных UФ напряжений. Так, в частности, между их действующими значениями имеется следующая связь:
UЛ = Ö 3 × UФ
В схеме «треугольник» линейные напряжения равны соответствующим фазным.
В последующих экспериментах изучаются напряжения и токи в трехфазных цепях с соединением «звезда» и «треугольник». Измеряются и рассчитываются обычно действующие значения напряжений и токов.
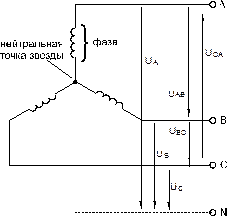
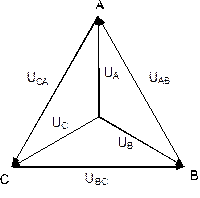
Рис. 8.1.3
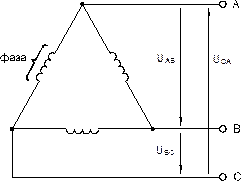
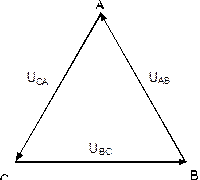
Рис. 8.1.4
Необходимое для экспериментов трехфазное напряжение частотой 50 Гц берется не непосредственно из питающей сети, а создается с помощью специального генератора синусоидальных напряжений. При этом из соображений электробезопасности величина линейного напряжения ограничена 12 В.
8.1.2. Экспериментальная часть
Задание
Выведите на дисплей виртуального осциллографа кривые фазных напряжений трехфазного источника, перенесите их на график, измерьте виртуальными приборами линейные и фазные напряжения и углы сдвига между фазными напряжениями.
Порядок выполнения эксперимента
· Соберите цепь согласно схеме (рис. 8.1.5), подключите выходы трехфазного генератора А и В к аналоговым входам коннектора V0 и V1.
· Включите виртуальные вольтметры V0 и V1 и осциллограф, установите пределы
измерений и развертки. Включите также виртуальный фазометр для измерения угла
сдвига фаз между напряжениями UA и UB.
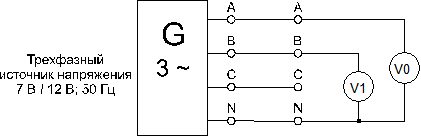
Рис. 8.1.5
· Перенесите на график (рис. 8.1.6) осциллограммы напряжений UA, UB, переключите вход коннектора V1 на фазу С и перенесите осциллограмму напряжения UC на график.
· Измерьте виртуальными вольтметрами все фазные и линейные напряжения, а также углы сдвига фаз между напряжениями UA и UB, UB и UC, UC и UA. Результаты измерений и расчетов занесите в табл. 8.1.1.
Рис. 8.1.6
Таблица 8.1.1.
| Измерения | Расчет | |
| UA, В | Среднее значение фазных напряжений: UФ = (UA + UВ + UС) / 3 = … В | |
| UB, В | ||
| UС, В | Среднее значение линейных напряжений: UЛ = (UAВ + UВС + UСА) / 3 = … В | |
| UАВ, В | ||
| UВС, В | Отношение UФ / UЛ = … | |
| UСА, В | ||
| yА – yВ, град | Средний угол сдвига между фазными напряжениями:
| |
| yВ – yС, град | ||
| yС – yА, град | ||
8.2. Трехфазная нагрузка, соединенная по схеме «звезда»
8.2.1. Общие сведения
Если нагрузки (приемники) соединены в трехфазную цепь по схеме «звезда» (рис. 8.2.1), то к сопротивлениям нагрузки приложены фазные напряжения. Линейные токи равны фазным и определяются по закону Ома:
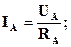
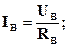
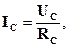
а ток в нейтрали равен векторной сумме этих токов: I N = I A + I B + I C.
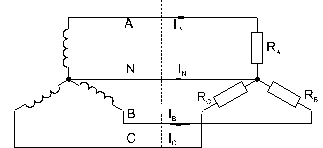
Рис. 8.2.1
При симметричных напряжениях UA, UB, UC и одинаковых сопротивлениях RA= RB = RC = R токи IA, IB, IC также симметричны и их векторная сумма (IN) равна нулю. Тогда
IЛ = IФ = UФ ¤ R; IN = 0.
Если же сопротивления фаз нагрузки неодинаковы, то через нулевой провод протекает некоторый ток IN ¹ 0. Это поясняется на векторных диаграммах (рис. 8.2.2).
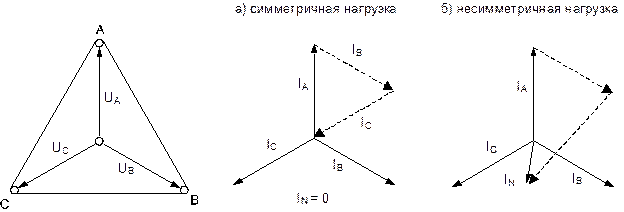
Рис. 8.2.2.
Мощность трёхфазной нагрузки складывается из мощностей фаз: S P = PА + PВ + PС.
Когда нагрузка симметричная и чисто резистивная, имеем
S P = 3 PФ = 3 UФ × IФ.
При смешанной (активно-индуктивной или активно-емкостной) нагрузке:
Активная мощность
S P = 3 × UФ × IФ × cos j = Ö3 × UЛ × IЛ × cos j.
Реактивная мощность
S Q = 3 × UФ × IФ × sin j = Ö3 × UЛ × IЛ × sin j.
Полная мощность
S S = 3 × UФ IФ = Ö3 × UЛ × IЛ .
8.2.2. Экспериментальная часть
Задание
Для трехфазной цепи с соединением «звезда» при симметричной и несимметричной нагрузках измерьте с помощью мультиметра или виртуальных приборов действующие значения токов IЛ и IN, а также напряжений UЛ и UФ, вычислите мощности PФ и S PФ, простройте векторные диаграммы.
Порядок выполнения эксперимента
· Соберите цепь с симметричной нагрузкой (RA = RB = RC = 1 кОм) согласно схеме (рис. 8.2.3).
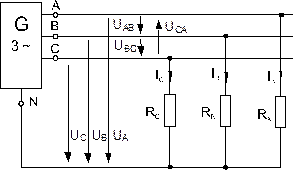
Рис. 8.2.3
· Измерьте действующие значения напряжений и токов согласно табл. 8.2.1 и вычислите мощности.
Таблица 8.2.1
| Схема «звезда» | Нагрузка симметричная | Нагрузка несимметричная | |
|
Линейные и фазные токи, ток нейтрали мА | IA | ||
| IB | |||
| IC | |||
| IN | |||
| Линейн. напряжения, В | UAB | ||
| UBC | |||
| UCA | |||
| Фазные напряжения, В | UA | ||
| UB | |||
| UC | |||
| Фазные мощности, мВт | PA | ||
| PB | |||
| PC | |||
| Общая мощность, мВт | SP | ||
· Повторите измерения и вычисления для несимметричной нагрузки (RA = 1 кОм, RB = 680 Ом, RC = 330 Ом).
· На рис. 8.2.4 в масштабе постройте векторные диаграммы.

Рис. 8.2.4.
8.3. Трехфазные нагрузки, соединенные по схеме «треугольник»
8.3.1. Общие сведения
Если нагрузки (приемники) соединены в трехфазную цепь по схеме «треугольник» (рис. 8.3.1), нагрузка RAВ, RBС и RCА каждой фазы включается на полное линейное напряжение, которое равно фазному UЛ = UФ
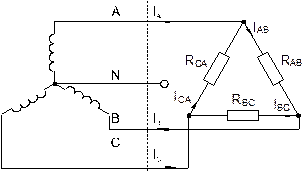
Рис. 8.3.1
Фазные токи IAВ, IBС и ICА определяются по закону Ома:
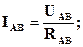
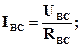
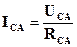 .
.
Линейные токи определяются по первому закону Кирхгофа:
I A = IAB – ICA; IB = IBC – IAB; IC = ICA – IBC.
При симметричных напряжениях UAВ, UBС, UCА и одинаковых нагрузках фаз RAВ = RBС = RCА = R токи также симметричны:
IФ = UФ / R; IЛ = IФ ¤ Ö3.
Это поясняется на векторных диаграммах (рис. 8.3.2).
Мощность S P, потребляемая трехфазной нагрузкой при ее соединении в «треугольник», складывается из мощностей фаз S P = PАВ + PВС + PСА..
При симметричной чисто активной нагрузке
S P = 3 × PФ = 3 × UФ × IФ.
При смешанной (активно-индуктивной или активно-емкостной) нагрузке:
Активная мощность
S P = 3 × UФ × IФ × cos j = Ö3 × UЛ × IЛ × cos j.
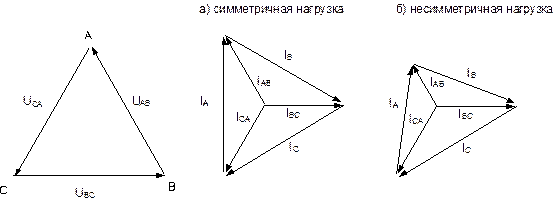
Рис.8.3.2.
Реактивная мощность
S Q = 3 × UФ × IФ × sin j = Ö3 × UЛ × IЛ × sin j.
Полная мощность
S S = 3 × UФ × IФ = Ö3 × UЛ × IЛ .
8.3.2. Экспериментальная часть
Задание
Для трехфазной цепи с соединением «треугольник» при симметричной и несимметричной омических нагрузках измерить с помощью мультиметра или виртуальных приборов действующие значения токов IЛ и IФ, а также напряжений UЛ, затем вычислить мощности PФ и S P.
Порядок выполнения эксперимента
· Соберите цепь с симметричной нагрузкой (RAВ = RBС = RCА = 1 кОм) согласно схеме (рис. 8.3.3). Для измерения шести токов (три фазных и три линейных) включите в цепь три виртуальных амперметра и три мультиметра в режиме измерения токов.
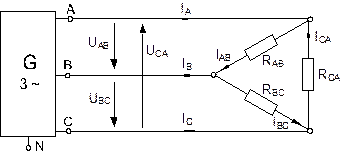
Рис. 8.3.3
· Измерьте мультиметром напряжения и токи согласно табл. 8.3.1 и вычислите мощности.
Таблица 8.3.1
| Схема «треугольник» | Нагрузка симметричная | Нагрузка несимметричная | |
|
Линейные токи, мА | IA | ||
| IB | |||
| IC | |||
|
Фазные токи, мА | IAB | ||
| IBC | |||
| ICA | |||
| Фазные и линейные напряжения, В | UAВ | ||
| UBС | |||
| UCА | |||
| Фазные мощности, мВт | PAВ | ||
| PBС | |||
| PCА | |||
| Общая мощность, мВт | SP | ||
· Повторите измерения и вычисления для несимметричной нагрузки (RA = 1 кОм, RB= 680 Ом, RC = 330 Ом).
· На рис. 8.3.4 в масштабе постройте векторные диаграммы.

Рис. 8.3.4.
8.4. Аварийные режимы трёхфазной цепи при соединении нагрузки в звезду
8.4.1. Общие сведения
Аварийными являются режимы, возникают при коротких замыканиях в нагрузке или в линиях и обрыве проводов. Остановимся на некоторых типичных аварийных режимах.