6.8.2 Экспериментальная часть
Задание
Снимите экспериментально частотные характеристики параллельного резонансного контура c высокой добротностью- I(w), IL(w), IC(w), X(w), Z(w)и j(w).
Порядок выполнения работы
- Соберите цепь согласно схеме (рис.6.8.3), включив в неё измерительные приборы или соответствующие гнёзда коннектора. В качестве катушки индуктивности с малым активным сопротивлением используйте обмотку трансформатора W=300 витков, вставив между подковами разъёмного сердечника полоски бумаги в один слой.
· Подайте на схему синусоидальное напряжение от генератора напряжений специальной формы U=5B, f=500Гц.
· Измерьте с помощью виртуальных приборов или рассчитайте по показаниям мультиметров реактивное сопротивление катушки индуктивности и рассчитайте индуктивность и резонансную частоту:
XL= U/ IL= Ом;
L= XL/(2 p f)= Гн;
f0=1/2 p √(LC)= Гц .
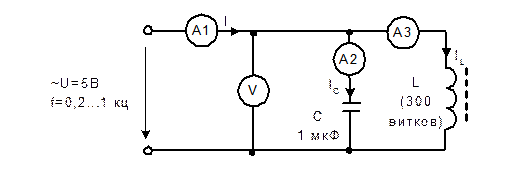
Рис. 6.8.3.
- По показанию фазометра или по минимуму тока I настройте резонансный режим, изменяя частоту приложенного напряжения.. Сравните экспериментальную резонансную частоту с расчётной:
Экспериментальная f0= Гц.
Расчётная f0= Гц.
- Изменяя частоту от 0,2 до 1 кГц, запишите в табл.6.8.1 показания виртуальных приборов и по этим результатам на рис. 6.8.4. и 6.8.5. постройте графики частотных характеристик.
Примечания:
1. При отсутствии виртуальных приборов запишите в таблицу измеренные мультиметрами токи, а сопротивления рассчитайте по формулам, приведённым в разделе «Общие сведения». При этом фазовый сдвиг можно определить из векторных диаграмм, построенных для каждого значения частоты.
2. В области резонансной частоты экспериментальные точки должны быть расположены гуще, чем по краям графиков.
| f, Гц | X, Ом | Z, Ом | I, мА | IC, мА | IL, мА | j, град |
Таблица 6.7.1.

6.9. Мощности в цепи синусоидального тока
6.9.1. Общие сведения
На рис. 6.9.1а изображена произвольная пассивная цепь синусоидального тока с двумя зажимами для подключения источника питания (пассивный двухполюсник).
В общем случае ток и напряжение на входе этой цепи сдвинуты по фазе на угол j:
u=Umsin( w t); i=Imsin( w t- j ).
Мгновенная мощность, потребляемая цепью от источника:
p= ui= UmImsin( w t) sin( w t- j)= UIcos j- UIcos(2 w t- j).
График изменения этой мощности представлен на рис. 6.9.1.б вместе с графиками изменения тока и напряжения. Мощность колеблется с двойной частотой. Большую часть периода она имеет положительное значение, а меньшую – отрицательное. Отрицательное значение мощности свидетельствует о возврате части накопленной в конденсаторах и катушках энергии в питающий цепь источник энергии.
Среднее значение потребляемой мощности:
P= UIcos j=I2 R
называется активной мощностью. Она характеризует среднюю скорость преобразования электрической энергии в другие виды энергии. Потребляемая в пассивной цепи активная мощность имеет всегда положительное значение. Она измеряется в ваттах (Вт).
Амплитуда переменной составляющей мощности:
S= UI= I2 Z
называется полной мощностью. Она характеризует максимальную мощность, на которую должен быть рассчитан источник для питания данной цепи. Её иногда называют кажущейся, габаритной или аппаратной мощностью. Единицей её измерения является вольт-ампер (ВА)
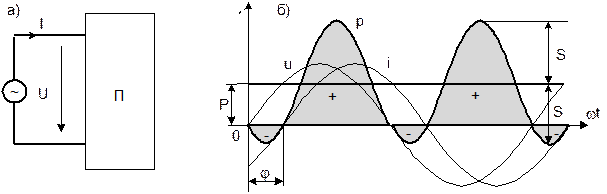 Рис. 6.9.1.
Рис. 6.9.1.
Величина Q= UIsin j=I2 X называется реактивной мощностью. Она характеризует максимальную скорость обмена энергии между источником и цепью. Она может быть как положительной (при j>0, т.е.в индуктивной цепи), так и отрицательной (при j<0, т.е. в ёмкостной цепи). В связи с этим иногда говорят, что индуктивность потребляет «реактивную энергию», а ёмкость вырабатывает её. Реактивная мощность измеряется в вольт-амперах реактивных (ВАр).
В электрической цепи синусоидального тока выполняется баланс как активных, так и реактивных (но не полных!) мощностей, т. е. сумма мощностей всех источников равна сумме мощностей всех потребителей:
S Pист .= S Pпотр.; S Qист .= S Qпотр..
Соотношения между различными мощностями в цепи синусоидального тока можно наглядно представить в виде треугольника мощностей (рис. 6.9.2).
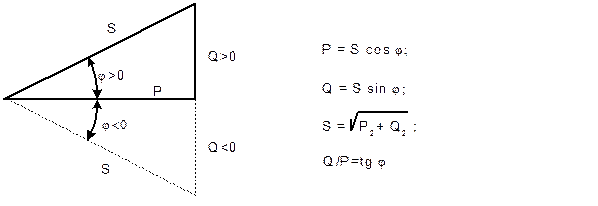
Рис.6.9.2
6.9.2. Экспериментальная часть
Задание
Измерьте с помощью виртуальных приборов мощности в цепи синусоидального тока . Расчётом проверьте баланс активных и реактивных мощностей.
Порядок выполнения работы
· Измерьте омметром активное сопротивление катушки индуктивности 40мГн:
.
Rк= Ом.
· Вычислите реактивные сопротивления катушки L=40 мГн и конденсатора
С=1 мкФ:
XL=2 p fL= Ом;
XC=1/2 p fC= Ом.
· Соберите цепь согласно схеме (рис. 6.9.3), включив в неё виртуальные приборы V1 и A1 и безразлично виртуальные или реальные А2 и А3.
· Подайте на схему синусоидальное напряжение 500 Гц и установите максимальную амплитуду, которую может дать генератор.
· Активизируйте виртуальные приборы: для измерения напряжения и тока на входе цепи, а также активной и реактивной мощности источника.
Примечание:
Избегайте включать одновременно большое количество виртуальных приборов в основном блоке. Это уменьшает количество отсчётов и снижает точность измерений!
· Запишите в табл 6.9.1 значения токов IRL, IR, IC и мощностей Рист и Qист.
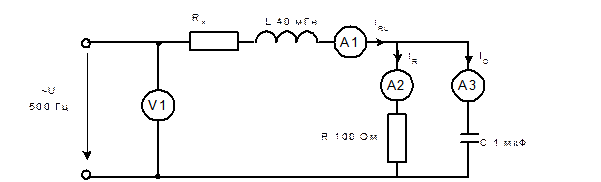
Рис.6.9.3.
Таблица. 6.9.1
| Ветвь | RкL | R | C |
Баланс мощностей, мВт, мВАр | |||
| I, мА | |||||||
| Р=I2R,мВт | 0 | Рист | SPпотр | ||||
| Q=I2X, мВАр | 0 | Qист | SQпотр | ||||
· Вычислите по приведённым в табл. формулам значения активной и реактивной мощностей каждого потребителя. Вычислите сумму активных и алгебраическую сумму реактивных мощностей их суммы и проверьте баланс мощностей.
7. Трансформаторы
Введение
Трансформатор состоит из двух или большего числа катушек (обмоток), магнитная связь, между которыми обеспечивается с помощью ферромагнитного сердечника. Трансформаторы используются для преобразования и согласования напряжений, токов и сопротивлений, а также для развязывания электрических цепей (гальваническая развязка).
В идеальном трансформаторе, то есть в трансформаторе без потерь, потребляемая им мощность равна мощности отдаваемой. В реальности, однако, имеют место потери мощности в меди обмоток (в омических сопротивлениях обмоток) и в сердечнике трансформатора, поэтому резистору нагрузки отдается только часть потребляемой трансформатором мощности.
7.1. Коэффициент магнитной связи
7.1.1. Общие сведения
Чтобы обеспечить требуемую магнитную связь между первичной и вторичной обмотками трансформатора, их помещают на общем сердечнике.

Рис. 7.1
Когда по первичной обмотке W1 протекает ток I1, то большая часть создаваемого им магнитного потока Ф0 сцепляется также и с витками вторичной катушки W2. Однако часть создаваемого первой катушкой потока Ф S замыкается, минуя вторую катушку. Эта часть потока называется потоком рассеяния.
Отношение
КСВ = Ф0 / (Ф0 + Ф S)
называется коэффициентом магнитной связи. Его можно выразить через напряжения U1 и U2 при холостом ходе и число витков:
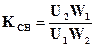
или через индуктивности и взаимную индуктивность
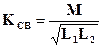 .
.
В идеальном трансформаторе коэффициент связи стремится к единице, однако равным или больше единицы он быть не может.
Во избежание искажения сигналов при их трансформировании и для исключения преждевременного магнитного насыщения материала сердечника постоянным током коэффициент связи уменьшают, разрывая сердечник (создавая воздушный зазор).
7.1.2. Экспериментальная часть
Задание
Измеряя напряжения, определите коэффициент магнитной связи между катушками
- при наличии замкнутого сердечника,
- при наличии сердечника с зазором,
- при наличии половины сердечника,
- при отсутствии сердечника.
Порядок выполнения эксперимента
·
|
|
|
Разместите первичную и вторичную катушки, имеющие по 900 витков каждая, на разъемном сердечнике, состоящем из двух половин, как показано на рис. 7.1.1.
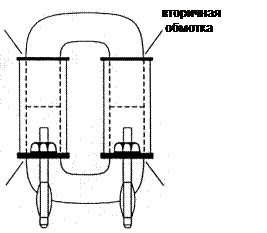 |
Рис. 7.1.1.
·
 |
Подсоедините источник синусоидального напряжения к выводам первичной обмотки согласно схеме (рис.7.1.2) и установите напряжение U1 = 6…7 В, f = 1 кГц.
Рис. 7.1.2.
· Измерьте мультиметром первичное и вторичное напряжения и занесите результат в таблицу 7.1.1 (строка «При наличии замкнутого сердечника»). Вычислите КСВ.
Таблица 7.1.1
| U1, В | U2, В | КСВ = U2/U1 | |
| При наличии замкнутого сердечника | |||
| При наличии сердечника с воздушным зазором | |||
| При наличии половины сердечника | |||
| При отсутствии сердечника |
· Для измерения напряжений при наличии сердечника с зазором поместите квадратики плотной бумаги между верхней и нижней половинами разъемного сердечника, чтобы имитировать воздушный зазор.
· Удалите одну подкову разъемного сердечника и повторите опыт.
· Удалите сердечник полностью и заполните последнюю строку табл. 7.1.1.
Вопрос: Почему изменяется вторичное напряжение?
Ответ: ………………..
7.2. Коэффициент трансформации
7.2.1. Общие сведения
Отношение числа витков первичной обмотки к числу витков вторичной обмотки трансформатора называют коэффициентом трансформации. Отношение чисел витков соответствует отношению первичного напряжения к вторичному при отсутствии нагрузки (холостом ходе) трансформатора и отношению вторичного тока к первичному при коротком замыкании.
В идеальном трансформаторе (при отсутствии потерь, при КСВ®1 и бесконечно больших индуктивностях обмоток L1 и L2) при любой нагрузке:
КТР = W1 / W2 = U1 / U2 = I2 / I1
7.2.2. Экспериментальная часть
Задание
Измеряя напряжения и токи, определите коэффициенты трансформации при различных числах витков обмоток.
Порядок выполнения эксперимента
· Соберите первичную (300 витков) и вторичную (100 витков) обмотки на разъемном сердечнике, как показано на рис. 7.2.1.
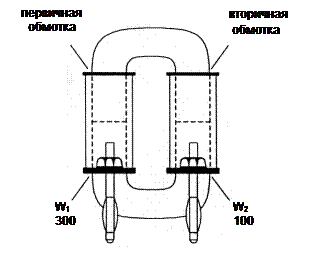 |
Рис. 7.2.1.
· Подключите источник питания к выводам первичной обмотки согласно рис. 7.2.3 и установите синусоидальное напряжение U1 = 6 В, f = 1 кГц.
 |
Рис. 7.2.3.
· Измерьте вторичные напряжения U2 на выводах вторичных обмоток с числами витков 100, 300 и 900 при холостом ходе. Занесите результаты в таблицу 7.2.1.
Таблица 7.2.1
| W1 | W2 | U1, В | U2, В | КТР |
| 300 | 100 | 6 | ||
| 300 | 300 | 6 | ||
| 300 | 900 | 6 |
· Вычислите значения коэффициента трансформации по формуле
КТР = U1 / U2
·
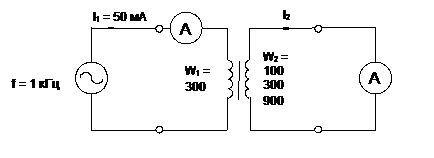 |
Проделайте опыт короткого замыкания, измерив первичные и вторичные токи при числах витков вторичной обмотки 100, 300 и 900, как показано на рис. 7.2.4 и занесите результаты измерений в таблицу 7.2.2. Ток I1 следует поддерживать неизменным, равным 50 мА.
Рис. 7.2.4.
КТР = I2 / I1
Таблица 7.2.2
| W1 | W2 | I1, мА | I2, мА | КТР |
| 300 | 100 | |||
| 300 | 300 | |||
| 300 | 900 |
7.3. Преобразование сопротивлений с помощью трансформатора
7.3.1. Общие сведения
Когда трансформатор ненагружен (холостой ход), отношение первичного напряжения к вторичному приблизительно равно отношению чисел витков первичной и вторичной обмоток. Коэффициент трансформации
КТР = U1 / U2 = W1 / W2
При нагрузке имеет место ток I2 в нагрузочном резисторе RН, подключенном к выводам вторичной обмотки. Этот ток вызывает появление соответствующего тока в первичной обмотке
I1 = I2 / КТР
Через первичные напряжение и ток можно найти входное сопротивление трансформатора
R1 = U1 / I1.
Нагрузочное сопротивление можно определить как
R2 = RН = U2 / I2.
Взяв отношение сопротивлений, получаем
R1 / RН = (U1 / I1) / (U2 / I2) = КТР 2
Или
R1 = RН × КТР2.
Это означает, что сопротивление нагрузки RН преобразуется к первичной стороне трансформатора. В реальном трансформаторе, если учесть сопротивление обмоток, получается R1 несколько больше, чем RНКТР2.
7.3.2. Экспериментальная часть
Задание
Определите величины сопротивлений R1 и R2, измеряя токи и напряжения на первичной и вторичной сторонах трансформатора при различных соотношениях чисел витков обмоток и значениях сопротивления нагрузки RН. Определите входное сопротивление как R2КТР2 и сравните его с R1.
Порядок выполнения эксперимента
· Соберите трансформатор на разъемном сердечнике с катушками, имеющими числа витков W1 = 300 и W2 = 100.
·
 |
Подключите источник питания, как показано на рис. 7.3, и установите синусоидальное напряжение U1 = 6 В, f = 1 кГц (при RН = 10 Ом).
Рис. 7. 3.
· Измерьте токи и напряжения при числах витков обмоток и сопротивлениях нагрузки согласно таблице 7.3.
Таблица 7.3
| W1 | W2 | КТР | RН, Ом | U1, В | U2, В | I1, мА | I2, мА | R1, Ом | R2, Ом | К2ТРR2 |
| 300 | 100 | 3 | 10 | |||||||
| 300 | 300 | 1 | 100 | |||||||
| 300 | 900 | 0,33 | 1000 |
· Вычислите сопротивления R1 и R2 по формуле R = U / I.
· Затем вычислите входное сопротивление по формуле К2ТР R2 и сравните его со значениями, найденными как U1 / I1.
·








