5.1. Напряжение и ток катушки индуктивности
5.1.1. Общие сведения
Когда к катушке индуктивности подведено синусоидальное напряжение, ток в ней отстает от синусоиды напряжения на ней на 900. Соответственно, мгновенное значение тока достигает амплитудного значения на четверть периода позже, чем мгновенное значение напряжения (рис. 5.1.1). В этом рассуждении пренебрегается активным сопротивлением катушки.
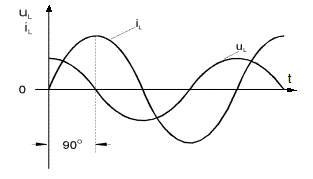
Рис. 5.1.1
5.1.2. Экспериментальная часть
Задание
Выведите на дисплей виртуального осциллографа кривые изменения во времени мгновенных значений тока iL и напряжения uL катушки индуктивности и определите фазовый сдвиг между ними.
Порядок выполнения эксперимента
· Соберите цепь согласно схеме (рис. 5.1.2), подключите к ее входу регулируемый источник синусоидального напряжения с параметрами: U=5В, f = 1 кГц.
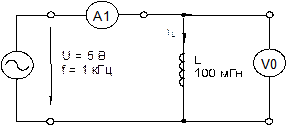
Рис. 5.1.2
· Включите виртуальные приборы V0, A1 и осциллограф.
· «Подключите» два входа осциллографа к приборам V0 и A1, а остальные отключите.
· Установите параметры развёртки осциллографа так, чтобы на экране было изображение примерно одного-двух периодов напряжения и тока.
· Перенесите данные осциллографирования напряжения и тока катушки на график (рис. 5.1.3), определите фазовый сдвиг между синусоидами напряжения и тока катушки индуктивности.
Рис. 5.1.3
Период
T =
Фазовый сдвиг
j =
Примечание: фазовый сдвиг меньше 90о из-за влияния активного сопротивления катушки.
· Включите блок дополнительных приборов, выберите из меню прибор «Угол сдвига фаз» и «подключите» его к V1 и А1. Убедитесь, что вы правильно определили фазовый сдвиг по осциллографу.
5.2. Реактивное сопротивление катушки индуктивности
5.2.1. Общие сведения
Катушка индуктивности в цепи переменного тока оказывает токоограничивающий эффект благодаря индуктируемой в ней противоЭДС. Этот токоограничивающий эффект принято выражать как индуктивное реактивное сопротивление (индуктивный реактанс) XL.
Величина индуктивного реактанса XL зависит от величины индуктивности катушки, измеряемой в Генри, и частоты приложенного напряжения переменного тока. В случае синусоидального напряжения имеем
XL = w L = 2 p fL ,
где XL - реактивное индуктивное сопротивление, Ом,
L - индуктивность катушки, Гн.
Если активное сопротивление катушки мало и им можно пренебречь, то реактивное (индуктивное) сопротивление можно определить через действующие значения или амплитуды напряжения и тока:
XL = UL ¤ IL или XL = ULm ¤ ILm.
5.2.2. Экспериментальная часть
Задание
Выведите на дисплей виртуального осциллографа кривые тока и напряжения различных катушек индуктивности при различных частотах и постройте зависимость XL = f( f). Соответствующий индуктивный реактанс находится по амплитудным значениям тока и напряжения из осциллограмм и проверяется по формуле XL = w L.
Порядок выполнения эксперимента
· Соберите цепь согласно схеме (рис. 5.2.1.), подсоедините к ее входу регулируемый источник синусоидального напряжения с параметрами U = 5 В, f = 1 кГц.
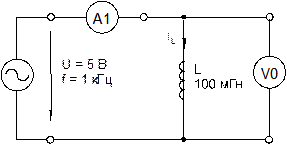
Рис. 5.2.1.
· Включите виртуальные приборы V0, A1 и осциллограф.
· «Подключите» два входа осциллографа к приборам V0 и A1, а остальные отключите.
· Установите параметры развёртки осциллографа так, чтобы на экране было изображение примерно одного-двух периодов напряжения и тока.
· Снимите с осциллограммы амплитудные значения Um и Im для индуктивностей и частот, указанных в табл. 4.2.1, и занесите их в соответствующие ячейки таблицы.
Таблица 5.2.1
| f, кГц | 0,5 | 1 | 1,5 | 2 | ||||||||||||
| UmL, В | 100 мГн |
|
|
|
| |||||||||||
| UmL, В | 40 мГн |
|
|
|
| |||||||||||
| UmL, В | 10 мГн |
|
|
|
| |||||||||||
| ImL, мА | 100 мГн |
|
|
|
| |||||||||||
| ImL, мА | 40 мГн |
|
|
|
| |||||||||||
| ImL, мА | 10 мГн |
|
|
|
| |||||||||||
| XL = Um ¤ Im, кОм | 100 мГн |
|
|
|
| |||||||||||
| 40 мГн |
|
|
|
| ||||||||||||
| 10 мГн |
|
|
|
| ||||||||||||
| XL = wL, Ком | 100 мГн |
|
|
|
| |||||||||||
| 40 мГн |
|
|
|
| ||||||||||||
| 10 мГн |
|
|
|
| ||||||||||||
· Вычислите величины XL по формулам Um ¤ Im и w L и занесите их в табл. 5.2.1.
· Перенесите величины XL на график (рис. 5.2.2) для построения кривой XL = f( f).

Рис. 5.2.2
Вопрос 1: Как зависит индуктивное сопротивление от частоты?
Ответ: ........................
Вопрос 2: Чем объясняется различие значений XL, вычисленных по формулам Um ¤ Im и w L?
Ответ: ........................








