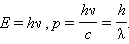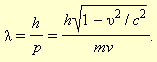. Луи де Бройль выдвинул гипотезу, что дуализм не является особенностью только оптических явлений, а имеет универсальный характер. Частицы вещества также обладают волновыми свойствами.
. Для частиц не очень высокой энергии, движущихся со скоростью 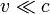 (скорости света), импульс равен
(скорости света), импульс равен 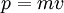 (где
(где 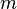 — масса частицы), и
— масса частицы), и 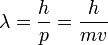 . Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость.
. Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость.
Длина волны де Бройля для нерелятивистской частицы с массой 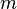 , имеющей кинетическую энергию
, имеющей кинетическую энергию 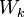
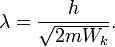
В частности, для электрона, ускоряющегося в электрическом поле с разностью потенциалов 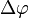 вольт
вольт
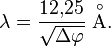
нерелятивистской частицы Свободные частицы — термин, который используется в физике для обозначения частиц, которые не взаимодействуют с другими телами, и имеют только кинетическую энергию.
Совокупность свободных частиц образовывает идеальный газ.
А волны де Бройля - это вообще не материальные образования. Для них в частности не действует запрет на сверхсветовые скорости. Это просто математика. во всех взаимодействиях частица проявляет себя именно как частица! "
Это, вообще говоря, неверно. Иначе не было бы повода говорить о корпускулярно-волновом дуализме. Есть ряд физических явлений, в которых частица взаимодействует как волна (например, всем хорошо известная дифракция и интерференция одиночных электронов и др. частиц - частица взаимодействует с препятствием, которое огибает).
Проводилось исследование отражения электронов от монокристалла никеля. Установка включала в себя монокристалл никеля, сошлифованный под углом и установленный на держателе. На плоскость шлифа направлялся перпендикулярно пучок монохроматических электронов. Скорость электронов определялась напряжением 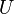 на электронной пушке:
на электронной пушке:
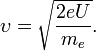
Под углом 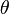 к падающему пучку электронов устанавливался цилиндр Фарадея, соединённый с чувствительным гальванометром. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме.
к падающему пучку электронов устанавливался цилиндр Фарадея, соединённый с чувствительным гальванометром. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме.
В опытах измерялась интенсивность рассеянного кристаллом электронного пучка в зависимости от угла рассеяния 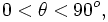 от азимутального угла
от азимутального угла 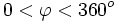 , от скорости
, от скорости  электронов в пучке.
электронов в пучке.
Таким образом наблюдалась дифракция электронов на кристаллической решётке монокристала. Опыт явился блестящим подтверждением существования у микрочастиц волновых свойств.
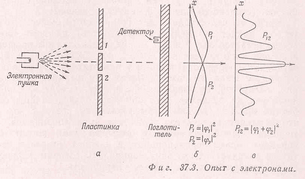
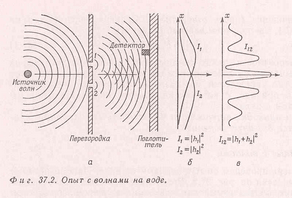
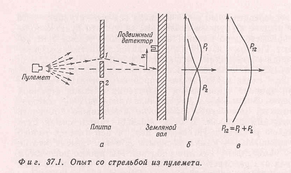
На третьем рисунке приводены результаты мысленных экспериментов с электронами при наличии двух щелей. Фейнман считал, что используя отличие в прохождении пуль и волн можно определить какого рода объект проходил через эти две щели. В опытах с волновыми свойствами частиц картина распределений получается не такими идеальными, как показано на третьем рисунке, однако точно установлено, что распределение при двух щелях отличается от суммы распределений попадания частиц при наличии каждой из щелей по отдельности. Сравнивая с опытами для пуль и для волн Фейнман делает вывод о том, что электроны обладает такими же свойствами, что и волны. Для анализа прохождения электронов при наличии двух щелей использовалась модель движения электронов в кулоновском поле зарядов,
Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами.
Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота ν и длина волны λ.
Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона:
|
Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны λ = h / p. Для частиц, имеющих массу,
| |
____________________________________________________________________
Канони́ческое коммутацио́нное соотноше́ние — в квантовой механике это соотношение между канонически сопряжёнными операторами, то есть операторами физических величин, являющимисядуальными относительно преобразования Фурье.
Например, каноническое коммутационное соотношение для оператора координаты частицы 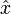 и оператора проекции её импульса на ось x
и оператора проекции её импульса на ось x 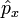 имеет вид:
имеет вид:
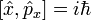
где квадратными скобками обозначен коммутатор:
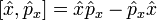
____________________________________________________________________
Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) в квантовой механике — фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих систему квантовых наблюдаемых, описываемых некоммутирующимиоператорами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределённостей[* 1] задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. Принцип неопределённости, открытый Вернером Гейзенбергом в1927 г., является одним из краеугольных камней квантовой механики.
Естественная ширина спектральной линии — ширина спектральной линии излучения, обусловленная взаимодействием с нулевыми колебаниями электромагнитного поля. Любая квантово-механическая система не может находиться сколь угодно долго в возбужденном состоянии. Естественная ширина линии определяется временем жизни возбужденного состояния, то есть интенсивностью его взаимодействия с полем.
В начале XX века учёные пришли к выводу, что между предсказаниями классической теории и экспериментальными данными об атомной структуре существует ряд расхождений. Открытие уравнения Шрёдингера последовало за революционным предположением де Бройля, что не только свету, но и вообще любым телам (в том числе и любым микрочастицам) присущи волновые свойства. Наиболее общая форма уравнения Шрёдингера — это форма, включающая зависимость от времени[1] :
Зависимое от времени уравнение (общий случай)
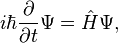
|
где 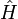 — гамильтониан.
— гамильтониан.
____________________________________________________________________
Волнова́я фу́нкция, или пси-функция 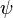 — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):
— комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):
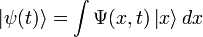
где 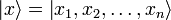 — координатный базисный вектор, а
— координатный базисный вектор, а 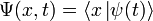 — волновая функция в координатном представлении.
— волновая функция в координатном представлении.
Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.
квантовая механика описывает не микрообъекты сами по себе, а их свойства, проявляющиеся в макроусловиях, создающихся классическими измерительными приборами в процессе акта наблюдения.
____________________________________________________________________
Поведение атомных объектов невозможно резко отграничить от их взаимодействия с измерительными приборами, фиксирующими условия, при которых происходят явления[4]
...в квантовой физике данные об атомных объектах, полученные при помощи разных экспериментальных установок, находятся в своеобразном дополнительном отношении друг к другу.[8]
...соотношения неопределённостей Гейзенберга...дают связь (обратную пропорциональность) между неточностями допустимого в квантовой механике фиксирования тех кинематических и динамических переменных, которыми в классической механике определяется состояние физической системы.[8]
____________________________________________________________________
1. Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений, таких, что интеграл 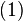 станет расходящимся. Следовательно, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.
станет расходящимся. Следовательно, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.
2. Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно. В задачах с использованием цилиндрической или сферической системы координат условие однозначности приводит к периодичности волновых функций по угловым переменным.
3. Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции 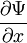 ,
, 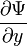 ,
, 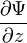 . Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.
. Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.
____________________________________________________________________
Ква́нтовая суперпози́ция (когерентная суперпозиция) — это суперпозиция состояний, которые не могут быть реализованы одновременно с классическойточки зрения, это суперпозиция альтернативных (взаимоисключающих) состояний. Принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции. Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными.
____________________________________________________________________
Квантовое состояние — любое возможное состояние, в котором может находиться квантовая система. Чистое квантовое состояние может быть описано:
· В волновой механике — волновой функцией,
· В матричной механике — вектором состояния, или полным набором квантовых чисел для определённой системы.
· Дисперсия (от лат. dispersio — рассеяние), в математической статистике и теории вероятностей, наиболее употребительная мера рассеивания, т. е. отклонения от среднего. В статистическом понимании Д.
· 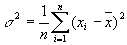
____________________________________________________________________
Гармонический осциллятор в квантовой механике представляет собой квантовый аналог простого гармонического осциллятора, при этом рассматривают не силы, действующие на частицу, агамильтониан, то есть полную энергию гармонического осциллятора, причём потенциальная энергия предполагается квадратично зависящей от координат. Учёт следующих слагаемых в разложении потенциальной энергии по координате ведёт к понятию ангармонического осциллятора.
____________________________________________________________________
Дискретный спектр энергетических уровней
Изменение энергии атома как квантовой системы характеризуется дискретностью, что обусловливает существование энергетических уровней (электронных слоев) и запрещенных энергетических зон между ними, ширина которых соответствует энергии фотона, излучаемого или поглощаемого электроном при "переходе" (квантовой телепортации) между уровнями.
____________________________________________________________________
Вакуум в современной квантовой теории поля означает основное, наинизшее состояние полей, описывающих соответствующие элементарные частицы. В квантовой электродинамике различают вакуум электромагнитного поля и вакуум электронно-позитронного поля. Из соотношения неопределенностей следует, что в состоянии вакуума поля совершают нулевые колебания, которые рассматриваются как состояния с виртуально возникающими парами частица-античастица.
Математически это явление для электромагнитного поля может быть представлено как совокупность независимых гармонических осцилляторов со всеми возможными значениями волнового вектора. При этом напряженность электрического поля играет роль скорости, а напряженность магнитного поля — координаты. Из квантовой механики следует, что осциллятор может находиться только в состояниях с дискретными значениями энергии: 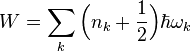 , где
, где 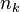 — число фотонов с волновым вектором k. В основном, наинизшем, состоянии электромагнитного поля фотоны отсутствуют, то есть
— число фотонов с волновым вектором k. В основном, наинизшем, состоянии электромагнитного поля фотоны отсутствуют, то есть 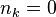 . При этом энергия электромагнитного поля в вакуумном состоянии оказывается бесконечно большой величиной
. При этом энергия электромагнитного поля в вакуумном состоянии оказывается бесконечно большой величиной 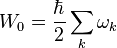 .
.
В квантовой электродинамике переходят к отсчету энергии не с нуля, а с нулевого уровня вакуумного состояния электромагнитного поля. Средние значения электрического и магнитного полей в вакуумном состоянии равны нулю, но средние значения квадратов этих величин больше нуля.
____________________________________________________________________
Тунне́льный эффект, туннели́рование — преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительно квантовой природы, невозможное в классической механике и даже полностью противоречащее ей. Аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрения геометрической оптики, происходит полное внутреннее отражение. Явление туннелирования лежит в основе многих важных процессов в атомной и молекулярной физике, в физике атомного ядра, твёрдого тела и
 прозрачность барьера физического соображения: эта величина идёт в показатель экспоненты со знаком минус, так что при переходе к классическому случаю барьер быстро становится непроницаемым.
прозрачность барьера физического соображения: эта величина идёт в показатель экспоненты со знаком минус, так что при переходе к классическому случаю барьер быстро становится непроницаемым.
____________________________________________________________________
В "релятивистской" динамике кинетическая энергия частиц определяется по двум формулам: первая идентифицирует полученную в электрическом поле энергию сразу в кинетическую Ek = mv2/2 = neU, гдеn - число раз прохождения зарядом e разности потенциалов U; вторая выражается через энергию массы покоя Ek = m0c2(1/ - 1).
Обе эти формулы позволяют расти массе и энергии ускоряемых частиц до бесконечности, что противоречит не только здравому смыслу, но и наблюдаемым явлениям. Рассмотрим следующее выражение для кинетической энергии Т , принимая во внимание, что скорость взаимодействия заряда е с электрическим полем с ростом скорости уменьшается как е.
T = m0 v2/2 = e U = eU (7)
Здесь е – заряд частицы; m0 – масса; U – разность потенциалов.
При v<<c T = eU. Найдём m0. m0 = 2eU/v2 , тогда (7) станет: Т/c2 = m0 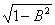 = m0(1 – v2/2c2). В первом приближении кинетическая энергия составит: T = m0c2 – m0v2/2 (8). Чтобы получить кинетическую энергию в чистом виде, добавим в левую часть (8) m0c2 + T = m0c2 – m0v2/2. T = - m0v2/2 (9).
= m0(1 – v2/2c2). В первом приближении кинетическая энергия составит: T = m0c2 – m0v2/2 (8). Чтобы получить кинетическую энергию в чистом виде, добавим в левую часть (8) m0c2 + T = m0c2 – m0v2/2. T = - m0v2/2 (9).
Вопреки утвердившемуся мнению, кинетическая энергия не прибавляется к энергии покоя, а вычитается, что соответствует нормальному превращению одного вида энергии в другой, в полном соответствии с законом сохранения энергии. При приближении v к с кинетическая энергия стремится к m0с2, а энергия покоя убывает до нуля.
Таким образом, кинетическая энергия ускоряемой частицы стремится только к величине энергии покоя, причём она отрицательна сама по себе. Полю Дираку не нужно иметь море виртуальных электронов, протонов, нейтронов и других античастиц с отрицательной кинетической энергией. Мы живём в мире с отрицательной кинетической энергией! Достаточно хорошо разогнать один электрон, чтобы его кинетическая энергия приблизилась к энергии покоя, тогда при встрече с электроном или ядром он доберёт недостающую энергию и, электрон, остановившись, так и остаётся электроном, а отрицательная кинетическая энергия рождает отрицательную частицу, подобную первой, но с другим знаком. Т.е., если это был электрон, то рождается позитрон, если протон – родится антипротон, нейтрон – антинейтрон и т.д. Рождение античастиц является прямым доказательством отрицательности кинетической энергии.
система замкнута и имеет прямоугольную форму, да еще и в возбужденном состоянии.
логично, что частица в подобной системе будет перемещаться циклично, а значит, что минимальной вероятность будет в каждом из двугранных углов.
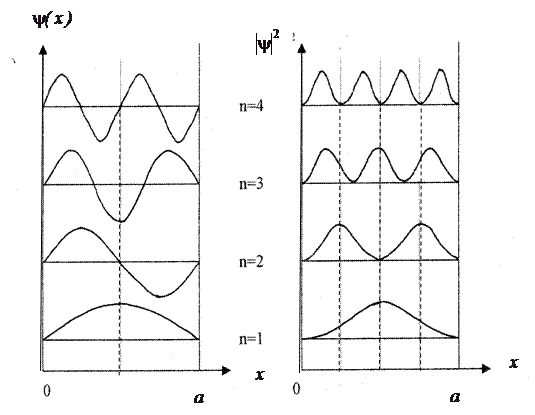
Рисунок 7.4.3. – График собственных функций
Рисунок 7.4.4. – График плотности обнаружения частицы в потенциальной яме
___________________________________________________________________
Уравнение Шрёдингера для частицы в одномерной потенциальной яме. Пусть частица массой m движется в потенциальном поле, вид которого изображен на рисунке 7.4.2. Движение частицы одномерное и ограничено непроницаемыми «стенками», говорят, что объект изучения находится в глубокой одномерной потенциальной «яме». Потенциальная энергия частицы вне и внутри потенциальной «ямы» имеет следующие значения: U = 0 для 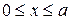 ; U= ; U= 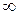 для для 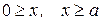 . .
|
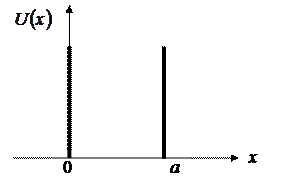 Рисунок 7.4.2. – Вид потенциального поля, называемого одномерной глубокой «потенциальной ямой»
Рисунок 7.4.2. – Вид потенциального поля, называемого одномерной глубокой «потенциальной ямой»
|
Уравнение Шрёдингера (стационарное) для одномерной задачи имеет вид: 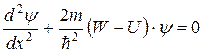 Волновая функция Волновая функция 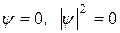 вне области вне области 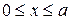 . Вероятность обнаружить частицу вне ямы равна нулю, поэтому, удовлетворяя требованиям конечности, однозначности и непрерывности пси–функции . Вероятность обнаружить частицу вне ямы равна нулю, поэтому, удовлетворяя требованиям конечности, однозначности и непрерывности пси–функции 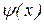 обращается в нуль и на стенках «ямы» обращается в нуль и на стенках «ямы» 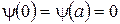 (краевые условия). Т.к. внутри ямы U=0, уравнение Шрёдингера имеет вид: (краевые условия). Т.к. внутри ямы U=0, уравнение Шрёдингера имеет вид: 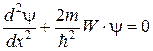 . .
|
Волновая функция для частицы в бесконечной потенциальной яме. Обозначим 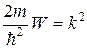 где где 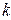 – волновое число волны де Бройля для частицы внутри потенциальной «ямы» и запишем решения уравнения в виде: – волновое число волны де Бройля для частицы внутри потенциальной «ямы» и запишем решения уравнения в виде: 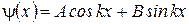 , где А иВ – постоянные. Используем первое краевое условие (для координаты , где А иВ – постоянные. Используем первое краевое условие (для координаты 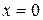 ): ): 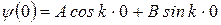 . Равенство возможно, если А=0. Из второго краевого условия (для координаты . Равенство возможно, если А=0. Из второго краевого условия (для координаты 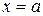 ): ): 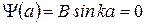 . Т.к. В≠0, следовательно, . Т.к. В≠0, следовательно, 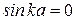 . Это возможно при . Это возможно при 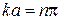 , где n=1, 2, 3….Отсюда , где n=1, 2, 3….Отсюда 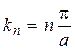 , т.е. волновое число может принимать только определенные значения кратные , т.е. волновое число может принимать только определенные значения кратные 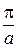 . Так как . Так как 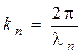 , где , где 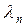 – длина волны де Бройля для частицы в «яме», то – длина волны де Бройля для частицы в «яме», то 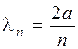 . Это означает, что на длине потенциальной «ямы» должно укладываться целое число полуволн де Бройля. . Это означает, что на длине потенциальной «ямы» должно укладываться целое число полуволн де Бройля.
|
Энергия частицы в бесконечной потенциальной яме. С одной стороны, 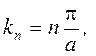 а с другой стороны, а с другой стороны, 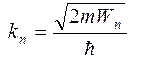 . Из этих соотношений определим энергию частицы. Энергия частицы в потенциальной «яме» имеет значения: . Из этих соотношений определим энергию частицы. Энергия частицы в потенциальной «яме» имеет значения: 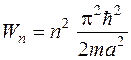 , т.е. она не произвольна, а принимает ряд дискретных значений: , т.е. она не произвольна, а принимает ряд дискретных значений: 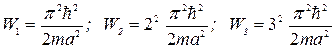 …… и т.д. Другие значения энергии невозможны, т.е. вероятность обнаружить внутри «ямы» частицу с энергией, отличной от значений …… и т.д. Другие значения энергии невозможны, т.е. вероятность обнаружить внутри «ямы» частицу с энергией, отличной от значений 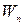 , равна нулю. Физические величины, принимающие определенные дискретные значения называются квантовыми. Квантовые значения Wn называются уровнями энергии. Числа n, определяющие энергетические уровни частицы называются квантовыми числами. Квантовое состояние с наименьшей энергией (n=1) называется основным состоянием.
____________________________________________________________________ , равна нулю. Физические величины, принимающие определенные дискретные значения называются квантовыми. Квантовые значения Wn называются уровнями энергии. Числа n, определяющие энергетические уровни частицы называются квантовыми числами. Квантовое состояние с наименьшей энергией (n=1) называется основным состоянием.
____________________________________________________________________
|
Энергетический спектр. Зависимость энергии частицы от каких либо параметров (например, квантового числа, частоты, длины волны) называется ее энергетическим спектром). Спектр может быть представлен и графически, и в виде формулы. Спектр частицы в бесконечной потенциальной яме дискретный. Значение энергии пропорционально квадрату квантового числа n. Расстояние между уровнями растет пропорционально n: 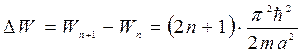 .
____________________________________________________________________ .
____________________________________________________________________
|
Плотность вероятности обнаружения частицы в бесконечной потенциальной яме. Волновые функции. Волновые функции или собственные функции уравнения имеют вид: 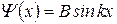 при любом значении х. Если учесть, что при любом значении х. Если учесть, что 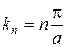 , то каждому значению kn соответствует своя волновая функция, т.е. , то каждому значению kn соответствует своя волновая функция, т.е. 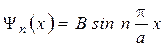 . Постоянная величина В определяется из условия нормировки . Постоянная величина В определяется из условия нормировки 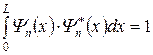 , она равна , она равна 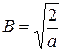 , следовательно, собственные функции стационарного уравненияШрёдингера внутри ямы равны: , следовательно, собственные функции стационарного уравненияШрёдингера внутри ямы равны: 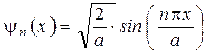 , , 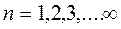 . Учитывая временную зависимость волновой функции, общий вид волновых функций для описания поведения частицы в бесконечной потенциальной яме: . Учитывая временную зависимость волновой функции, общий вид волновых функций для описания поведения частицы в бесконечной потенциальной яме: 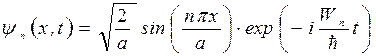 . Плотность вероятности. Из этого следует, что волновая функция зависит от времени гармонически, что приводит к тому, что вероятность нахождения частицы . Плотность вероятности. Из этого следует, что волновая функция зависит от времени гармонически, что приводит к тому, что вероятность нахождения частицы 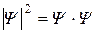 * не зависит от времени. Функция * не зависит от времени. Функция 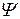 * является комплексно сопряженной функции * является комплексно сопряженной функции 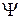 . Такие состояния называются стационарными. Графики собственных функций изображены на рисунке 7.4.3. Графики плотности вероятности нахождения частицы в том или ином месте «ямы» при различных значениях энергии представлены на рисунке 7.4.4. Анализ рисунка 7.4.4 показывает, что в основном состоянии (n=1) частицу с наибольшей вероятностью можно найти в середине «ямы». При (n=2) плотность вероятности обнаружить частицу в центре «ямы» равна нулю, т.е. частица с энергией . Такие состояния называются стационарными. Графики собственных функций изображены на рисунке 7.4.3. Графики плотности вероятности нахождения частицы в том или ином месте «ямы» при различных значениях энергии представлены на рисунке 7.4.4. Анализ рисунка 7.4.4 показывает, что в основном состоянии (n=1) частицу с наибольшей вероятностью можно найти в середине «ямы». При (n=2) плотность вероятности обнаружить частицу в центре «ямы» равна нулю, т.е. частица с энергией 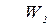 не будет появляться в центре ямы. Этот результат резко отличается от того, что ожидается для макроскопической частицы, которую можно обнаружить с равной вероятностью в любом месте «ямы». При увеличении квантового числа n максимумы не будет появляться в центре ямы. Этот результат резко отличается от того, что ожидается для макроскопической частицы, которую можно обнаружить с равной вероятностью в любом месте «ямы». При увеличении квантового числа n максимумы 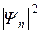 располагаются все ближе друг к другу, так что при больших значениях n получится распределение вероятности, соответствующее макроскопической частице. В этом находит свое выражение принцип соответствия: при больших квантовых числах выводы и результаты квантовой механики должны соответствовать классическим результатам. располагаются все ближе друг к другу, так что при больших значениях n получится распределение вероятности, соответствующее макроскопической частице. В этом находит свое выражение принцип соответствия: при больших квантовых числах выводы и результаты квантовой механики должны соответствовать классическим результатам.
|
Функции , удовлетворяющие уравнению Шредингера при данных U, называются собственными функциями.
Значения Е, при которых существуют решения уравнения (22), называются собственными значениями.
В качестве примера определим и Е для свободной частицы.
Свободной называют частицу, на которую не действуют силы, т.е. 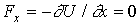 . Cледовательно, U(x)=const и ее можно принять равной нулю. Таким образом, в случае свободного движения частицы, ее полная энергия совпадает с кинетической, а скорость
. Cледовательно, U(x)=const и ее можно принять равной нулю. Таким образом, в случае свободного движения частицы, ее полная энергия совпадает с кинетической, а скорость 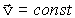 . Направим ось Х вдоль вектора
. Направим ось Х вдоль вектора 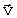 . Тогда (22) можно записать в виде
. Тогда (22) можно записать в виде
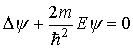 . (23)
. (23)
Прямой подстановкой можно убедится, что частным решением этого уравнения является функция(х)=Аexp(ikx), где А=сonst, k=const c собственным значением энергии
Е= 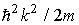 .(24)
.(24)
C учетом (21) волновая функция
(х)=Аexp(-it+ ikx)= Аexp[-(i/ 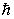 )(Еt- рxх)]. (25)
)(Еt- рxх)]. (25)
здесь =Е/ 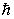 , k=рx/
, k=рx/ 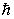
Функция (25) представляет собой плоскую монохроматическую волну де Бройля [cм. (16)].
Из (24) следует, что зависимость энергии от импульса
Е= 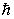 2k2/(2m)=Рх2/(2m)=mv2/2 (26)
2k2/(2m)=Рх2/(2m)=mv2/2 (26)
оказывается обычной для нерелятивиских частиц. Следовательно, энергия свободной частицы может принимать любые значения, т.е. ее энергетический спектр является непрерывным.
Плотность вероятности обнаружить частицу в данной точке пространства
|| 2=*=A2,
т.е. все положения свободной частицы в пространстве являются равновероятными.
____________________________________________________________________
Квантовые числа - это числа, возникающие при решении уравнения Шрёдингера. Они служат для описания квантово-химической модели ядра атома, в простейшем случае - ядра атома водорода (протона) Каждая орбиталь характеризуется набором трёх квантовых чисел n, l, ml, а состояние электрона в атоме - теми же тремя + ещё одним, дополнительным числом ms (итого, четыре).
Главное квантовое число n определяет энергию электрона на разрешённых атомных орбиталях. Кроме того, через энергию мы можем рассчитать и размер области нахождения электрона. Решение уравнения Шрёдингера даёт выражение для расчёта энергии электрона.
E = -2пи: 2me^4/n^2h^2 = -1312,1/n^2 кДж/моль (для атома водорода) . Оно получается подстановкой конкретных значений чисел в радиальную часть уравнения Шрёдингера. Из чего следует, что n принимает натуральные значения (1, 2, 3 и т. д. )
____________________________________________________________________
Орбитальное квантовое число l характеризует энергетический подуровень. Также характеризует момент количества движения электрона на орбитали относительно выбранного направления в пространстве с волновой точки зрения по x, y или z. Для решения уравнения l может принимать целые значения от 0 до n-1. Спектроскописты выделяют ещё одно значение квантового числа l. Оно характеризует вырождение или расщепление квантового уровня на энергетические подуровни. Это не число, а вид. Число l также определяет форму энергетической орбитали.
____________________________________________________________________
Магнитное квантовое число ml (принимающие целые значения от -l до l) отвечает за проекцию количества движения на выбранное направление в пространстве. Магнитное число говорит о том, как данное облако ориентировано в пространстве, а также самой орбитали.
Кроме трёх квантовых чисел собственное поведение электрона, проявляющееся в некоторых опытах, проявляется четвёртым квантовым числом ms, которое называют магнитным спиновым числом. Это число может принимать только два значения: 1/2 и -1/2. Если говорить просто, оно показывает, в какую сторону вращается электрон в данном квантовом состоянии, характеризующимся только тремя квантовыми числами. В таком состоянии могут находиться не более двух электронов согласно принципу Паули. Причём оба они вращаются в разные стороны - отсюда спиновое число одного - положительно, другого - отрицательно.
Эти четыре квантовых числа полностью предполагают энергетическое и геометрическое описание свойств в атоме. Образом (или пространственным представлением) и является атомная орбиталь.
При падении электрона на протон угловая скорость движения электрона неограниченно возрастает, что должно приводить к сплошному спектру излучения, неограниченному по частоте.
Все эти выводы противоречат опыту, что показывает невозможность классической теории правильно описать свойства атома водорода. Первый шаг в понимании закономерностей движения электрона в атоме водорода был сделан Бором, который дополнил классические уравнения (II.4.1) – (II.4.4) уравнением квантования момента импульса электрона
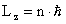 , n = 1,2, … , (II.4.8)
, n = 1,2, … , (II.4.8)
которое после подстановки в (II.4.6) даёт дискретный энергетический спектр для финитного движения электрона
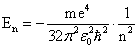 , n=1,2,3, … .
, n=1,2,3, … .
ереход электронов из состояния финитного движения с дискретным спектром в состояние инфинитного движения со сплошным спектром называется ионизацией. Минимальная энергия, которую необходимо передать электрону в стационарном состоянии с энергией En для того, чтобы произошла ионизация атома водорода, определяется соотношением
____________________________________________________________________
Гиромагни́тное отноше́ние (магнитомехани́ческое отноше́ние) — отношение дипольного магнитного момента элементарной частицы (или системы элементарных частиц) к её механическому моменту.
В системе СИ единицей измерения гиромагнитного отношения является с·А·кг−1 = с−1·Тл−1. Часто подразумевается, что гиромагнитное отношение измеряется в единицах q/2mc, где с — скорость света, q и m — заряд и масса частицы, соответственно. В этом случае оно выражается безразмерной величиной.
Для различных состояний атомной системы гиромагнитное отношение определяется формулой:
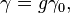
где g — множитель Ланде, γ0 — единица гиромагнитного отношения:
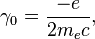
где e — элементарный заряд, me — масса электрона, с — скорость света.
В случае ядер, за единицу гиромагнитного отношения принимают величину:
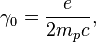
где mp — масса протона.
Согласно классической теории, гиромагнитное отношение является коэффициентом пропорциональности между угловой скоростью прецессии магнитного момента, помещённого во внешнеемагнитное поле, и вектором магнитной индукции.
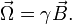
____________________________________________________________________
Состояния с одинаковой энергией называют вырожденными, а число различных состояний с определенным значением энергии Еп - кратностью вырожденияданного энергетического уровня. Кратность вырождения n-го уровня водородоподобной системы можно определить, учитывая число возможных значений ℓ и т.Каждому из п значений квантового числа ℓ соответствует 2ℓ + 1 значений т. Поэтому полное число N различных состояний для данного п равно
N = 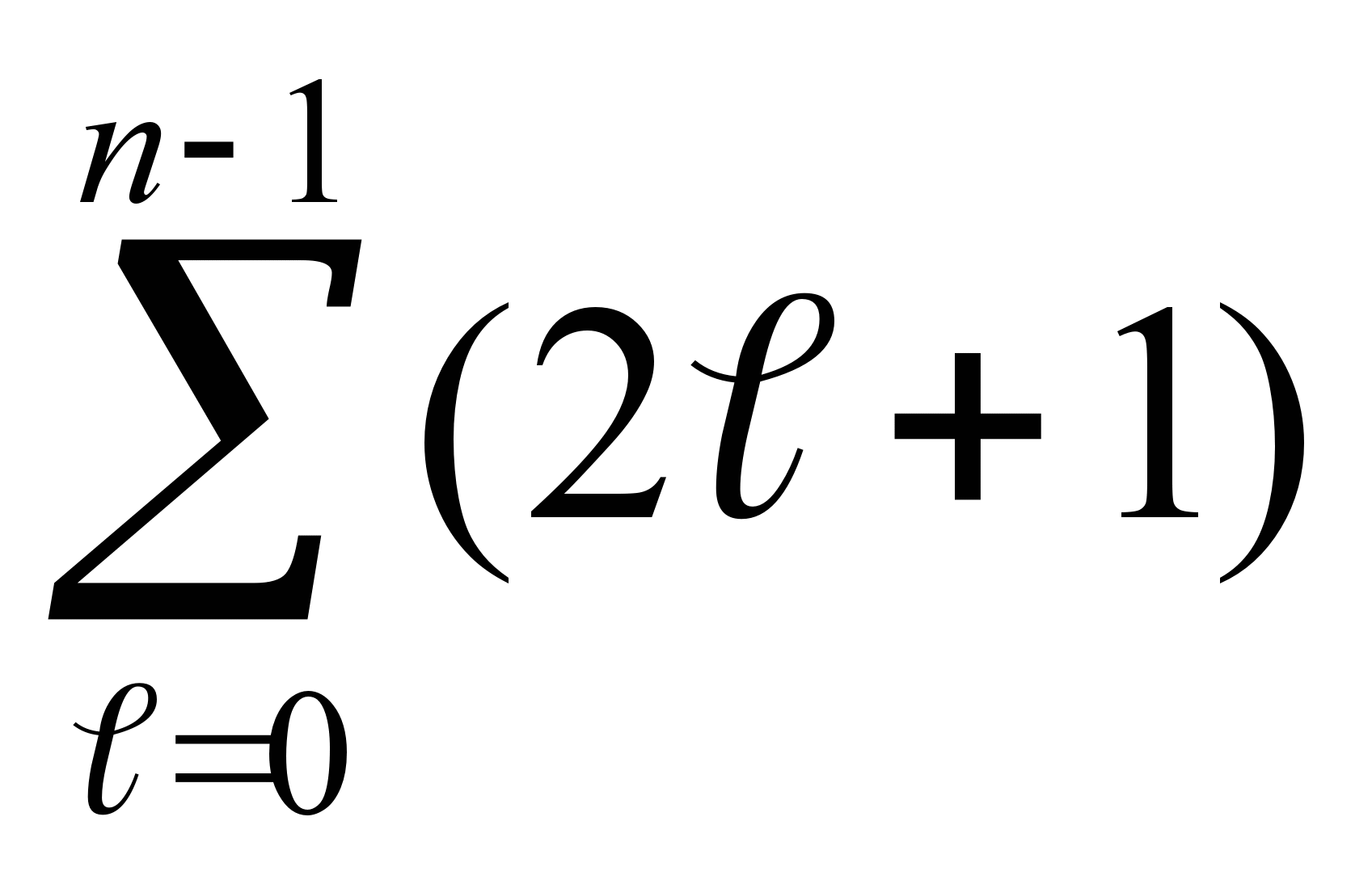 = 1 + 3 + 5 + ... + (2п - 1) = п2. = 1 + 3 + 5 + ... + (2п - 1) = п2.
|
Электронная оболочка атома — область пространства вероятного местонахождения электронов, характеризующихся одинаковым значением главного квантового числа n и, как следствие, располагающихся на близких энергетических уровнях. Число электронов в каждой электронной оболочке не превышает определенного максимального значения.
Порядок заполнения электронных оболочек (орбиталей с одинаковым значением главного квантового числа n) определяется правилом Клечковского, порядок заполнения электронами орбиталей в пределах одного подуровня (орбиталей с одинаковыми значениями главного квантового числа n и орбитального квантового числа
____________________________________________________________________
Правилами отбора в спектроскопии называют ограничения и запрет на переходы между уровнями квантомеханической системы с поглощением или излучением фотона, наложенные законами сохранения и симметрией. Разрешенные переходы гармонического осциллятора удовлетворяют правилу отбора:
____________________________________________________________________
Спин (от англ. spin — вертеть[-ся], вращение) — собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы.
Спин измеряется в единицах ħ (приведённой постоянной Планка, или постоянной Дирака) и равен 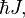 где J — характерное для каждого сорта частиц целое (в том числе нулевое) или полуцелое положительное число — так называемое спиновое квантовое число, которое обычно называют просто спином (одно из квантовых чисел).
где J — характерное для каждого сорта частиц целое (в том числе нулевое) или полуцелое положительное число — так называемое спиновое квантовое число, которое обычно называют просто спином (одно из квантовых чисел).
В связи с этим говорят о целом или полуцелом спине частицы
____________________________________________________________________
Взаимодействие спинового и орбитальных магнитных моментов посредством магнитного поля (спин – орбитальное взаимодействие) приводит к сдвигу и расщеплению энергетических уровней, определяемых формулами (II.4.14)-(II.4.16). В результате возникает тонкая структура энергетического спектра атома водорода с характерной энергией
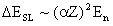 , где
, где 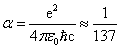 - постоянная тонкой структуры, Z – заряд ядра (для атома водорода Z=1) и En – энергия стационарного состояния (II.4.14). Из (II.4.21) следует что спин-орбитальное взаимодействие играет важную роль для сверхтяжелых элементов.
- постоянная тонкой структуры, Z – заряд ядра (для атома водорода Z=1) и En – энергия стационарного состояния (II.4.14). Из (II.4.21) следует что спин-орбитальное взаимодействие играет важную роль для сверхтяжелых элементов.
____________________________________________________________________
Электроны обладают собственным (спиновым) моментом импульса (1) и собственным магнитным дипольным моментом (2)
В выражениях (1) и (2) е— элементарный заряд, me— масса покоящегося электрона,
s—спиновое квантовое число. При написании выражения (2) учтено, что ; (3)
магнетон Бора — элементарный магнитный дипольный момент, Знак минус в формуле (2) указывает на то, что направления магнитного и механического спиновых моментов вследствие отрицательности заряда электрона противоположны.
Атом водорода — физическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра может входить протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон преимущественно находится в тонком концентрическом шаровом слое вокруг атомного ядра, образуя электронную оболочку атома. Наиболее вероятный радиус электронной оболочки атома водорода в стабильном состоянии равенборовскому радиусу a0 = 0,529 Å.
Атом водорода имеет специальное значение в квантовой механике и релятивистской квантовой механике, поскольку для него проблема двух тел имеет точное или приближенное аналитическое решения. Эти решения применимы для разных изотопов водорода, с соответствующей коррекцией.
____________________________________________________________________
Движущееся отрицательное или положительное волновое возмущение поля в один квант заряда представляет электрический ток смещения, поэтому может двигаться только по замкнутой боровской орбите - ток, согласно законам электродинамики, всегда замкнут. При этом орбитальное движение совершает только энергия (масса) электрического потока, магнитный же поток создается круговым током смещения и не движется, поэтому масса магнитного потока не участвует в образовании момента количества движения - спина, т.е. возникает "удвоенный магнетизм" спина. В электромагнитной волне энергия (масса) электрического потока равна энергии (массе) магнитного потока. Отсюда спин электрона: L = mcRe/2 = h/4π, где Re - эффективный радиус орбиты, по которому движется электрическое возмущение поля Re = h/2πmc.
____________________________________________________________________
Каждый электрон в атоме обладает орбитальным моментом импульса  и собственным моментом
и собственным моментом  Механические моменты связаны с соответствующими магнитными моментами, вследствие чего между всеми
Механические моменты связаны с соответствующими магнитными моментами, вследствие чего между всеми 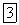 имеется взаимодействие.
имеется взаимодействие.
Моменты  складываются в результирующий момент атома
складываются в результирующий момент атома  При этом возможны два случая.
При этом возможны два случая.
1. Моменты  взаимодействуют между собой сильнее, чем с
взаимодействуют между собой сильнее, чем с  которые в свою очередь сильнее связаны друг с другом, чем с
которые в свою очередь сильнее связаны друг с другом, чем с  Вследствие этого все
Вследствие этого все  складываются в результирующую
складываются в результирующую  моменты
моменты  складываются в
складываются в  а затем уже
а затем уже  дают суммарный момент атома
дают суммарный момент атома  Такой вид связи встречается чаще всего и называется связью Рёссель — Саундерса или
Такой вид связи встречается чаще всего и называется связью Рёссель — Саундерса или  вязью.
вязью.
2. Каждая пара  взаимодействует между собой сильнее, чем с другими
взаимодействует между собой сильнее, чем с другими  вследствие чего образуются результирующие
вследствие чего образуются результирующие  для каждого электрона в отдельности, которые затем уже объединяются в
для каждого электрона в отдельности, которые затем уже объединяются в  атома. Такой вид связи, называемый
атома. Такой вид связи, называемый  вязью, наблюдается у тяжелых атомов.
вязью, наблюдается у тяжелых атомов.
Сложение моментов осуществляется по квантовым законам (см. § 24). Рассмотрим подробнее сложение моментов в случае связи Рёссель — Саундерса.
Орбитальные квантовые числа U всегда бывают целыми. Соответственно квантовое число L суммарного орбитального момента также бывает целым (либо нулем).
____________________________________________________________________
JJ-связь - это один из типов векторной связи, при котором взаимодействие орбитального (момент импульса) и спинового моментов каждого электрона в электронной оболочки сильнее, чем взаимодействие порознь орбитального и спинового моментов различных электронов между собой. Относится к однородным типам связи. Данный тип векторной связи используется для описания уровней энергии тяжёлых атомов и многозарядных ионов.
СВЯЗЬ ВЕКТОРНАЯ - наглядная модель векторного сложения орбитальных li и спиновых siмоментов в полный момент J квантовой системы (атома, атомного ядра, молекулы), характеризующая взаимодействие электронов в атомах и молекулах и нуклонов в атомных ядрах.
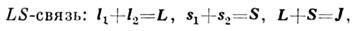
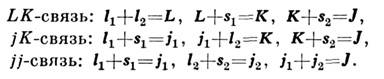
____________________________________________________________________
Магнитный момент, основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки
____________________________________________________________________
Комбинации пространственных (орбитальных) состояний частиц в коллективе легко описать разными способами. Возможные спиновые комбинации в системе двух частиц-фермионов с половинным спином (электронов, протонов) можно представить разными способами. Можно изобразить ориентации спинов разными символами (стрелками, знаками или греческими буквами). Результат сложения компонент момента импульса вдоль оси вращения представим в одной из строк таблицы значениями суммарного магнитного квантового числа.
____________________________________________________________________
Правила и примеры построения векторных диаграмм
Для определения группы соединения следует прежде всего построить векторные диаграммы для обмоток ВН и НН. Считаем, что векторная диаграмма напряжений ВН всегда задана в виде треугольника междуфазовых напряжений АВ, ВС и СА, точнее, в виде взаимного расположения вершин А, В и С (рис. 7,а). Тогда условимся, что положительным направлением векторов фазных напряжений обмотки ВН, соединенной в Y, является направление от точки О к вершинам А, В и С, т. е. векторы OA, OB и ОС.
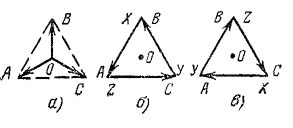
____________________________________________________________________
При́нцип Па́ули , согласно которому два и более тождественных фермиона(частиц с полуцелым спином) не могут одновременно находиться в одном квантовом состоянии.
____________________________________________________________________
Фе́рми — Дира́ка то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяетраспределение вероятностей нахождения фермионов на энергетических уровнях системы, находящейся в термодинамическом равновесии; предложена в позволяет найти вероятность, с которой фермион занимает данный энергетический уровень. 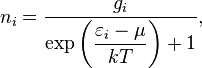
где
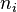 — среднее число частиц в состоянии
— среднее число частиц в состоянии 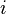 ,
,
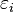 — энергия состояния
— энергия состояния 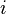 ,
,
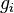 — кратность вырождения состояния
— кратность вырождения состояния 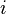 (число состояний с энергией
(число состояний с энергией 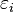 ),
),
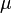 — химический потенциал (который равен энергии Ферми
— химический потенциал (который равен энергии Ферми 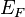 при абсолютном нуле температуры),
при абсолютном нуле температуры),
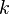 — постоянная Больцмана,
— постоянная Больцмана,
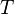 — абсолютная температура.
— абсолютная температура.
В (идеальном) ферми-газе в пределе низких температур 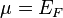 . В этом случае (полагая уровни энергии невырожденными
. В этом случае (полагая уровни энергии невырожденными 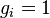 ), функция распределения частиц называется функцией Ферми:
), функция распределения частиц называется функцией Ферми:
Два класса Элементарные частицы, в узком смысле - частицы, которые нельзя считать состоящими из других частиц. В современной физике термин "элементарные частицы" используют в более широком смысле: так называют мельчайшие частицы материи, подчиненные условию, что они не являются атомными ядрами и атомами (исключение составляет протон); иногда по этой причине элементарные частицы называют субъядерными частицами. Большая часть таких частиц (а их известно более 350) являются составными системами. И неэлементарные