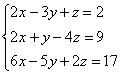Формулы Крамера для системы линейных уравнений
Рассмотрим систему уравнений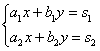 
На первом шаге вычислим определитель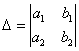 
, его называют главным определителем системы.
Если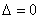 
, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если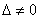 
, то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
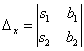и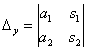 
Корни уравнения находим по формулам:
, 
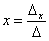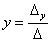
Пример. Решить систему линейных уравнений
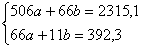
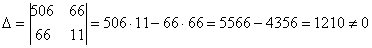, значит, система имеет единственное решение.
;
; 
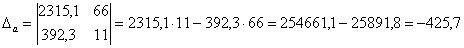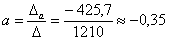
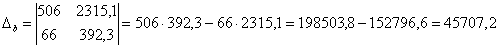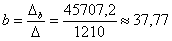
Ответ: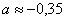 
, 
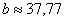
Обязательным фрагментом оформления задания является следующий фрагмент: «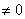 
, значит, система имеет единственное решение».
Домашнее задание. Решить систему по формулам Крамера. Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
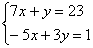
Правило Крамера для системы трех уравнений с тремя неизвестными:
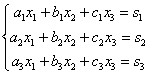
Находим главный определитель системы:
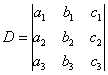
Если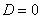 
, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если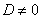 
, то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, 
, 
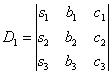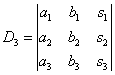
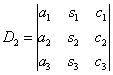И, наконец, ответ рассчитывается по формулам:
, 
, 
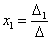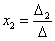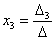
Случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов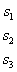 
последовательно перемещается слева направо по столбцам главного определителя.
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по такому же принципу.
Пример. Решить систему по формулам Крамера.
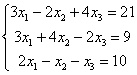
Решение:
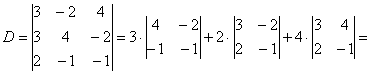
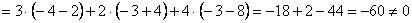, значит, система имеет единственное решение.
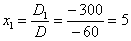
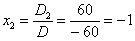
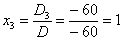
Ответ: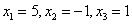 
.
Домашнее задание. Решить систему по формулам Крамера.
