Стойкость инструмента как случайная переменная величин.

Дата: 2025-05-01; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Стойкость инструмента является переменной величиной, которая может принимать для одного и того же инструмента в одинаковых условиях эксплуатации различные значения.

Стойкость определяется двумя факторами:

1. Качеством инструмента, которое создается в процессе изготовления в виде определенной совокупности физико-механических, конструктивных и геометрических параметров.

2. Условиями эксплуатации (свойством обрабатываемого материала, режимами обработки, жесткостью системы и т.п.).

Влияние на стойкость этих факторов различно по силе и направлению. Все это определяет стойкость как случайную переменную величину.

Обычно для характеристики величины стойкости пользуются некоторым средним ее значением. Однако значение среднего арифметического не является полной характеристикой переменной величины.

Практика эксплуатации АЛ показывает, что знание средней стойкости не позволяет рассчитывать, например, период принудительной замены инструмента, его надежность.

Случайная величина полностью описывается, если задан закон ее распределения, т.е. соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующим им вероятностями.

Для описания закона распределения стойкости можно использовать несколько теоретических распределений, которые не противоречат результатам эксперимента:

- нормальное распределение;

- экспоненциальное распределение;

- распределение Вейбулла - Гнеденко;

- гамма - распределение;

- логарифмическое нормальное распределение;

- распределение Бернштейна;

- альфа – распределение.

Все эти распределения при определенных условиях стремятся к нормальному распределению.

В виду жесткого ограничения слева нулем, что объясняется тем, что стойкость не может принимать отрицательных значений, этот закон будет необходимо усеченным. Вот почему альфа – распределение представляет особый интерес и во многих случаях получило как теоретическое, так и практическое подтверждение.

Выражение закона распределения плотности стойкости инструмента для альфа – распределения имеет вид:

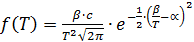, где

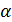, β – параметры распределения, определяют опытным путем;

е – основание натуральных логарифмов;

с – постоянная;

α – характеризует ассиметрию;

β – характеризует размах кривой;

с – подсчитывается из условия, чтобы площадь под кривой равнялась 1.

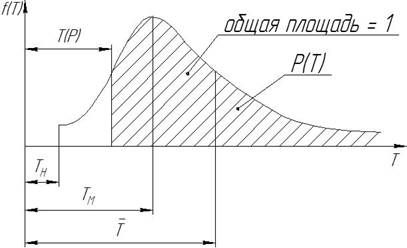
Р(Т) – площадь соответствует надежности Р.

Т_Н - надежная стойкость;

Т_М - наиболее вероятная (медианная) стойкость;

Т – стойкость любая (текущая), аргумент;

Т(Р) – стойкость с заданной вероятностью безотказной работы в течении Т;

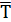– среднеарифметическая стойкость;

β – относительный запас стойкости (пропорциональный Т);

α – коэффициент однородности скорости износа,

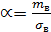, где

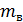- средняя скорость износа;

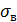- среднее квадратическое отклонение скорости износа.

С ростом α пик острее, разброс меньше.

С ростом β кривая сдвигается вправо и растягивается.

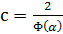, где 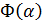- интеграл вероятности.

Значение функции надежности Р(Т) определяется на основании плотности распределения стойкости из следующего условия:

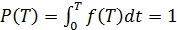или

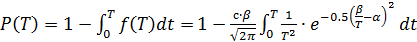
Применив подстановку: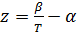

Получаем: 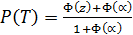- вероятность безотказной работы в течение времени Т. Закон распределения, и его параметры определяются опытным путем.

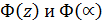- соответствующие табличные функции интеграла вероятностей.

Формулы, вытекающие из анализа закона:

;

;

.

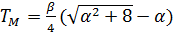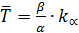α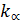
2	1,25
3 и более	1

Пример: определим величину стойкости сверл ø 20 мм с распределением α=0,26 и β=100. Уровень вероятности которой 0,95.

По таблице интеграла вероятности: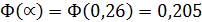

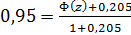, отсюда 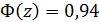→ по таблице интеграла вероятности 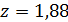, отсюда .

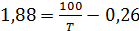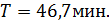
Таким образом, с вероятностью 0,95 сверла данной партии будут иметь стойкость не ниже 46,7 мин. Надежность режущего инструмента в производственных условиях оценивается количественно значением функции надежности Р (Т) на основе установленных параметров α и β распределения стойкости f (Т).

7. Износ режущего инструмента и связанные с ним изменения размеров детали и потери времени.

В результате износа инструмент не только теряет свою способность снимать стружку, но и изменяет размер обрабатываемой поверхности.

Как уже было отмечено, различают общую стойкость, после работы в течение которой инструмент надо заменить новым, и размерную стойкость Т_р, после работы в течение которой размер детали выходит из поля допуска.

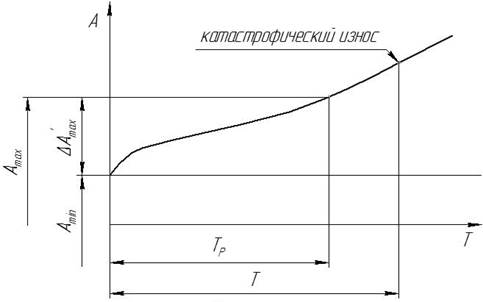
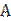- размер детали;

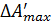- наибольшее допустимое изменение размера.

Изображенная кривая является идеализированной, абстрактной, т.к. не учитывает следующих факторов:

1. В любой момент времени τ размер детали не равен точно размеру А, а подчинен нормальному закону распределения, т.к. является случайной величиной с дисперсией σ² (σ – среднеквадратичное отклонение).

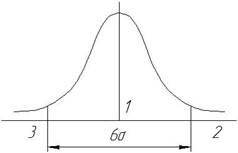1 – центр группировки размера;

2 – верхняя граница поля рассеивания;

3 – нижняя граница поля рассеивания.

2. Случайные отклонения от размера А в разные моменты времени различны.

При износе инструмента из-за вырастания сил резания, увеличения температуры σ – увеличивается.

3. Настроить инструмент так, чтобы 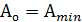в начале обработки невозможно. Всегда, во избежание неисправимого брака инструмент будет несколько “отодвинут” от нижней границы поля допуска, т.е. .

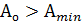Учитывая это, диаграмма точности (точностная диаграмма) имеет вид (рис.3): 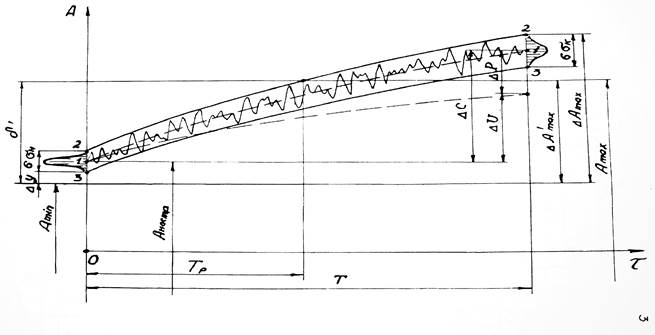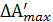– наибольшее допускаемое изменение размера;

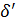– технологический допуск;

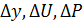– систематические погрешности;

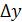– погрешность первоначальной настройки – постоянная систематическая погрешность;

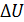– размерный износ вершины резца;

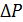– упругие деформации, вызванные возрастанием сил резания.

В результате сложения этих погрешностей размерная стойкость существенно уменьшается, т.к. увеличивается 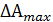- наибольшее изменение размера за период стойкости.

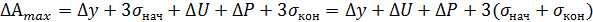
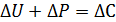- переменная систематическая погрешность, вызванная износом инструмента (износом вершины и ростом сил резания).

1 – линия центров группирования случайных погрешностей (текущая среднего размера обрабатываемых деталей);

2, 3 – верхняя и нижняя границы поля рассеивания размеров, вызванного случайными погрешностями.

В обычном процессе, когда за станком стоит рабочий, изменения размеров устраняются им самим, поэтому обычно, если с затуплением инструмента шероховатость не увеличивается сверх заданного предела, размерная стойкость Т_р → Т.

Так как Т_р < Т, то для полного использования периода стойкости Т производится несколько подналадок инструмента, т.е. его перемещения “на деталь”.

Частота (число) подналадок (минимальная) за период стойкости:

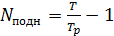(при ; ).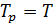

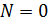Размерная стойкость т.о. является комплексной характеристикой технологического процесса, учитывающей:

- допуск на обработку (Т↑ с ↑ );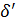

- точность настройки – установки инструмента на размер 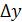(с увеличением погрешности настройки ↓);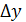

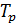- точность и жесткость системы СПИД ( с ухудшением характеристик СПИД ↓);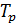

- износостойкость и конструкционно-геометрические параметры инструмента.

Применением специальной оснастки 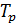может быть повышена, а в ряде случаев доведена до Т.

Рассматривая диаграмму точности, можно получить представление о тех потерях времени, которые возникают из-за износа инструмента, и наметить пути их уменьшения.

Эти потери:

a) Первая наладка инструмента на размер А_настр (настройки);

b) Подналадка в течении периода стойкости N_подн и каждая занимает какое-то время;

c) Смена инструмента на новый в конце периода Т (и снова первая наладка на размер А_настр и т.д. цикл повторяется).

8. Первоначальная настройка инструмента на размер.

Смысл операции первоначальной настройки заключается в том, чтобы установленный на станок определенным образом инструмент имел положение режущей кромки и вершины таким, которое обеспечивает получение размеров в пределах допуска и максимальный запас на его износ.

Размер первой детали партии или в других случаях положения инструмента на станке перед обработкой детали в партии, при котором обеспечивается возможный запас инструмента на износ называется оптимальным настроечным размером.

Условие возможности настройки:

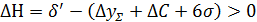(погрешность настройки).

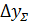- сумма постоянных систематических погрешностей;

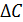- переменная систематическая погрешность;

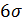- случайная погрешность.

Если 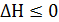, то мы не можем предварительно настроить инструмент, обеспечивая автоматическое получение размеров всех деталей партии.

В идеальном случае для обработки валика оптимальный настроечный размер равен наименьшему предельному размеру, т.е. 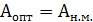, а для отверстия 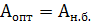, если бы не было рассеивания и погрешности настройки.

В реальных случаях надо стремиться, чтобы А_настр → к выгодной границе поля допуска с учетом имеющихся погрешностей.

Погрешность настройки 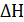является тоже случайной величиной при настройке инструментов много раз в начале обработки. И у нее есть тоже среднее квадратичное отклонение .

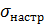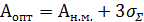– вал.

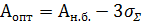– отверстие.

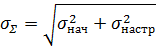
9. Способы настройки на .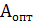

Различают динамические и статистические способы настройки.

Динамические – настройку ведут путем пробной обработки деталей.

Статистические – не связанные с обработкой детали.

Динамические методы настройки .

1) Производственный метод настройки (метод пробных проходов). Большие потери времени. Не происходит настройки на оптимальный размер из-за боязни получить неисправимый брак. Размерная стойкость Т_р ↓.

2) 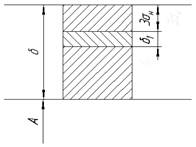Применение специальных калибров для первоначальной настройки инструментов. Проектируют специальные калибры с уменьшенным полем допуска додвинутым к выгодной границе.

Широкого распространения метод не нашел.

Калибр для настройки отличается от контрольного калибра.

3) Настройка по результатам измерения пробной партии деталей. Берется партия 5-10 шт. и обрабатывается с одной настройкой резца. Измеряют детали прибором с ценой деления ( 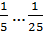)δ.

Далее определяется средний размер:

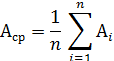
Находим разброс размера: .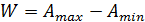

Определяем среднее квадратичное отклонени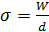е: , где

d – делитель зависит от значения n.

Оптимальный настроечный размер:

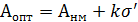- наружная обработка;

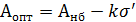- внутренняя обработка.

Значение k :

Наружная обработка: токарные станки k=2,7;

Внутренняя обработка: расточные станки k=1,8;

токарные станки k=3,1;

шлифовальные станки k=3,6.

Поправка: .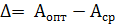

Если 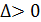, надо отодвинуть резец от центра на .

После корректировки резца на величину Δ обрабатываем еще малую партию (3…5 шт.) и далее также снова.Если 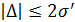- настройка считается законченно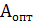й. и 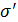указываются в технологических картах.

Метод производительный (производительность увеличивается на 15%), повышается размерная стойкость, уменьшаются простои. (Широко применяется на ЗИЛе).

10. Способы настройки на .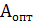

Различают динамические и статистические способы настройки.

Динамические – настройку ведут путем пробной обработки деталей.

Статистические – не связанные с обработкой детали.

Статистические методы настройки.

Не требуют обработки пробных деталей. При этом уменьшаются потери времени.

Различают две группы методов настройки:

1. Настройка инструмента непосредственно на станке.

2. Настройка инструмента вне станка.