Математика 5-Б класс
Урок № 24 Дата. 11.11.2021г.
Тема урока: Деление нацело
Алгоритм изучения темы
1) Теоретический материал для самостоятельного изучения:
В начальной школе вместе с действием умножения вы изучали и другое арифметическое действие второй ступени — деление.
Вспомните: (устно)
Как называются компоненты при делении?
(число, которое делят, называется делимым , а то, на которое делят, — делителем. Результат действия деления называется частным).
Умножение и деление — взаимно обратные действия. Именно поэтому умножение проверяют делением, а деление — умножением.
Как найти неизвестные компоненты умножения?, деления?.
Давайте вспомним, что нам уже известно об операции деления. Пусть у нас есть натуральные числа a и b, причём а больше b или равно b (a ≥ b).
Определение: а делится на b нацело, если существует натуральное число с, при умножении которого на b получается а.
Обычно слово «нацело» в этой фразе опускается. При этом записывают: a : b = с и называют а – делимым, b – делителем, с – частным.
Любое натуральное число а делится на 1 и само на себя:
а : 1 = а , а : а = 1
так как а ∙ 1 = а, 1 ∙ а = а.
Например, 14 делится на 1 и на 14.
14 : 1 = 14, 14 : 14 = 1
При делении ноля на любое натуральное число получается ноль: 0 : а = 0, потому что 0 ∙ а = 0.
Запомните: делить на нуль нельзя!
Любое натуральное число а делить на нуль нельзя, потому что не существует такого числа с, для которого выполнялось бы равенство а : 0 = с (так как с ∙ 0 = 0 ≠ а). Принято считать, что нуль на нуль делить нельзя.
Для деления чисел из двух и более цифр (знаков) применяют деление уголком.
Вспомним, как делить уголком, на примере.
Вычислим 392 : 28 = ?
Для начала запишем делимое и делитель уголком:
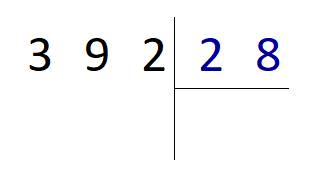
Начнём делить 392 на 28 следующим образом.
Во-первых, определим неполное частное. Для этого слева направо сравниваем цифры делимого и делителя.
Рассмотрим цифру 3. Она меньше 28 – значит, нужно взять ещё одну цифру из делимого. 39 больше 28, следовательно, это неполное частное.
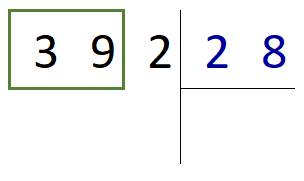
Ставим точку в частном (под уголком делителя).
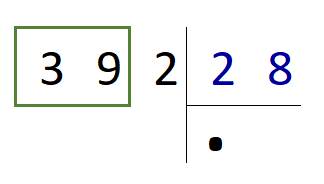
Посчитаем, сколько цифр осталось в делимом, после неполного частного. У нас после 39 стоит только одна цифра – 2. Значит, и в результат добавляем ещё одну точку.
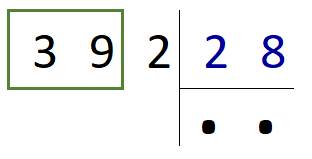
Приступаем к делению: 28 помещается в 39 только один раз, поэтому ставим первой цифрой ответа единицу и вычитаем 28 из 39.
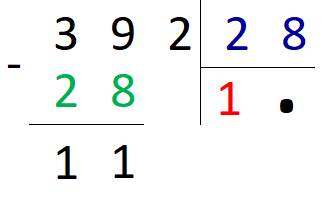
После вычитания в остатке получилось 11, это меньше, чем 28, поэтому к 11 дописываем 2.
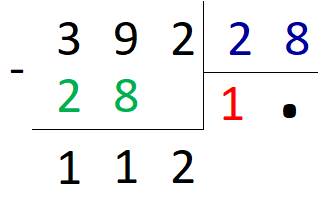
112 делится на 28. Получаем 4. Записываем полученный результат второй цифрой в ответе.
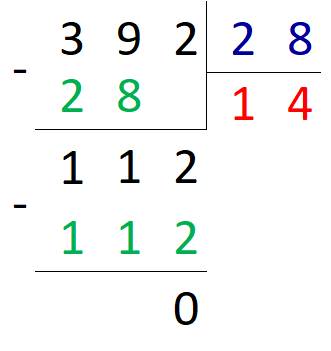
В остатке получился нуль – значит, числа разделились нацело. Таким образом, 392 : 28 = 14.
Важное свойство частного: делимое и делитель можно одновременно умножить или разделить на одно и то же натуральное число: частное от этого не изменится.
Вычислим 50 : 25 = ?
Сначала одновременно умножим 50 и 25 на 2. Получим:
100 : 50 = 2.
Теперь разделим 50 и 25 на 5. Получим:
10 : 5 = 2.
В обоих случаях ответ оказался одинаковым. Значит, свойство частного верно.
Если каждое из натуральных чисел a и b делится на натуральное число с, то верно равенство:
(a+ b) : c = a : c + b : c.
Убедимся в правдивости данного свойства на примере.
Вычислим выражение: 124 : 4 + 36 : 4.
Рассмотрим два способа решения.
1 способ. Выполним деление и сложим результаты.
124 : 4 + 36 : 4 = 31 + 9 = 40.
2 способ. Заметим, что у нас есть общий делитель – 4. Вынесем его за скобки. Получим:
(124 + 36) : 4 = 160 : 4 = 40.
В обоих случаях у нас получился один и тот же ответ. Значит, свойство верно.
| ЗАПИШИТЕ В ПАМЯТКУ |
Любое натуральное число а делится на 1 и само на себя:
а : а = 1, т.к. а ⋅ 1 = а;
а : 1 = а, т.к. 1 ⋅ а = а;
0 : а = 0, т.к. а ⋅ 0 = 0;
а : 0 – нельзя.
Свойство частного.








