Федеральное государственное автономное образовательное
МИНОБРНАУКИ РОССИИ
Федеральное государственное автономное образовательное
учреждение высшего образования
«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ РАДИОТЕХНИЧЕСКИХ СИСТЕМ И УПРАВЛЕНИЯ
КАФЕДРА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Отчет
по лабораторной работе №4
«Исследование переходных процессов импульсной системы управления»
по курсу:
«Теория автоматического управления»
Выполнили:
Студенты группы РТбо3-7
Кошкальда Я.Ю.
Гладышев Д.А.
Проверил:
Ассистент каф. САУ
Денисенко Д. Ю.
__________________
Таганрог 2017 г.
Цель работы: Изучение методов математического описания, анализа и моделирования импульсных систем управления. Изучение переходных процессов в импульсных системах.
Ход работы:
Рис. 1. - Структурная схема гидросистемы
Коэффициент передачи непрерывной части: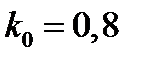 
В структурной схеме исследуемой системы заменяем импульсный элемент звеном с коэффициентом передачи, равным 1. Находим переходную функцию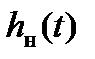 
получившейся линейной непрерывной системы и определяем по ней время переходного процесса, которое обозначим 
.
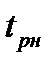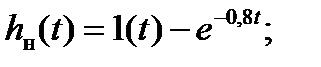
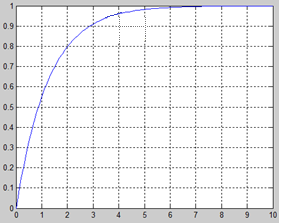
Рис.2-График переходной функции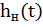 
рассматриваемой системы
Таким образом, по переходной характеристике видно, что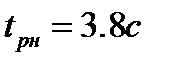 
Запишем уравнения в переменных состояния непрерывной части системы:
Непрерывная часть рассматриваемой системы описывается уравнениями
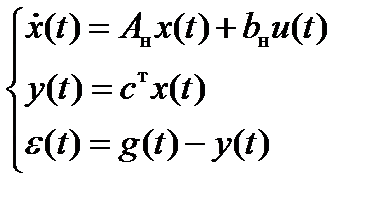
Исходя из передаточной функции непрерывной части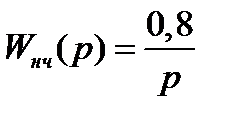 
, запишем уравнения переменных состояния в канонической управляемой форме
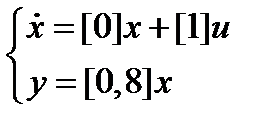
Разностные уравнения исследуемой системы в разомкнутом состоянии:
так как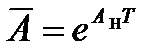 
, 
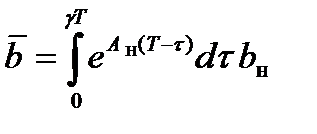, то
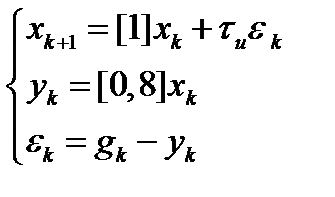
В замкнутом состоянии:
так как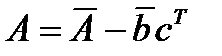 
, 
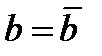, то
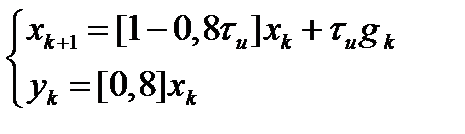
Соответствующие передаточные функции исследуемой системы:
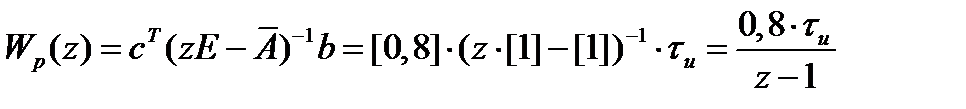
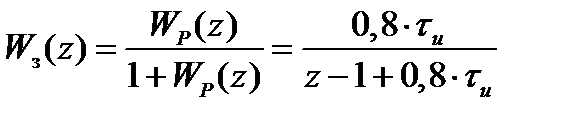
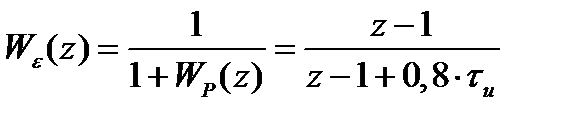
По найденной матрице 
определяем характеристический полином системы:
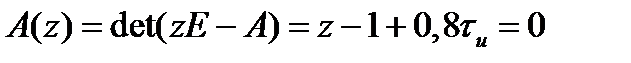
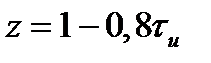
По условию устойчивости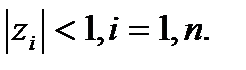 
будем иметь 
.
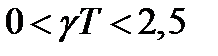при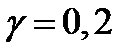 
;
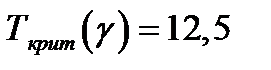при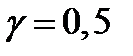 
;
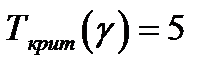при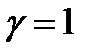 
.
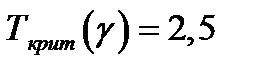В аналитическом виде переходная функция будет выглядеть:
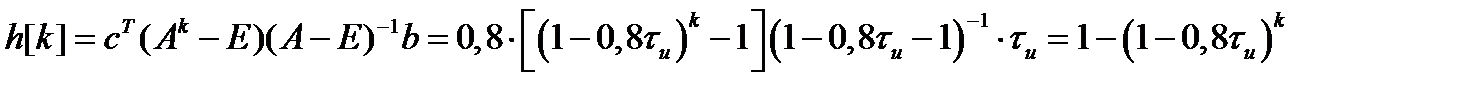
Принимаем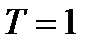 
; 
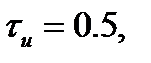и строим график 
:
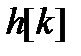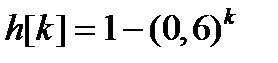
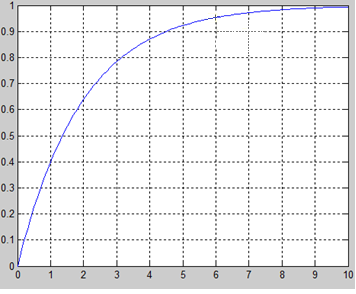
Рис.3-График переходной функции 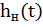рассматриваемой системы.
По переходной характеристике видно, что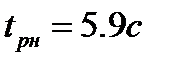 
.
Для нахождения переходной функции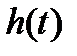 
импульсной системы при любых значениях t применим формулу Коши общего решения уравнений состояния непрерывной части системы на интервалах знакопостоянства управления:
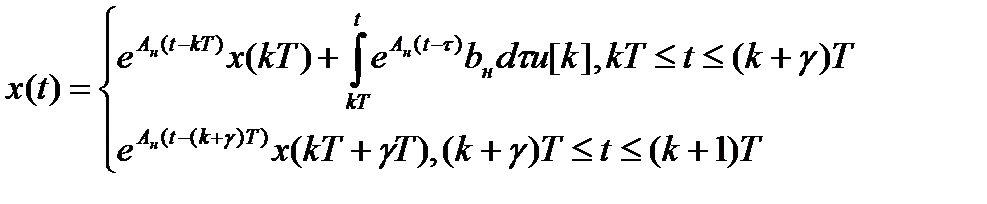
где x[0] = 0, u[k] = 1-h[k], k = 0,1,2…, h(t) = x(t)
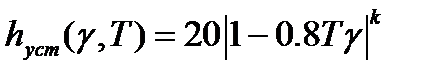
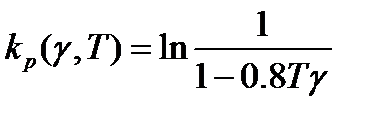
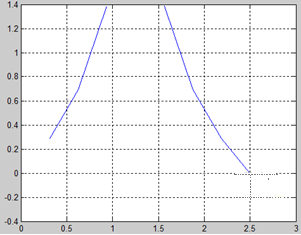
Рис.4-График зависимости функции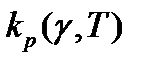 
.
По графику видно, что Kp min= -0.2231. Из формулы 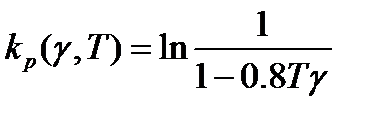выражаем T:
T=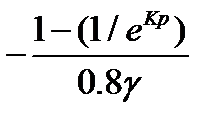 
Подставляем 
и Kp min получаем:
При =0,2 T0( )=1.56;
При =0,6 T0( )=0.52;
При =0,9 T0( )=0.35;
Зададимся периодами дискретизации исходя из следующих выражений:
T1( ) 
T0( ) T2( ) и T3( ) > Tкрит( )
При =0,2 T1( )=1, T2( )=3, T3( )=14;
При =0,6 T1( )=0.4, T2( )=2, T3( )=7;
При =0,9 T1( )=0.1, T2( )=1.5, T3( )=6;
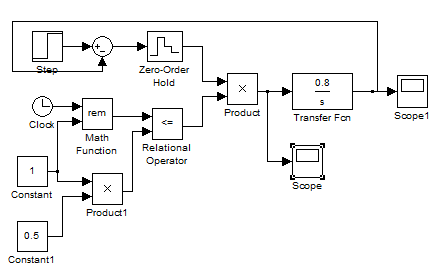
Рис.5-схема гидросистемы в Simulink.
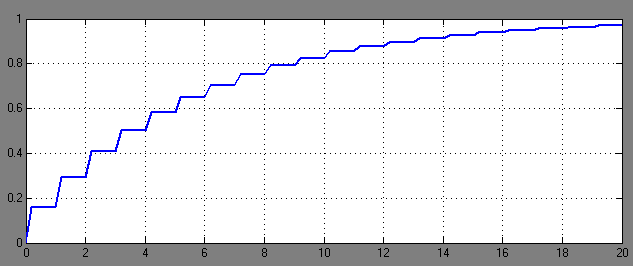
Рис.6-График переходного процесса при =0,2 и Т=1.(tр ≈17с).
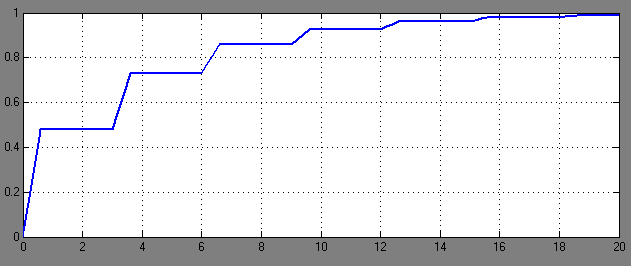
Рис.7-График переходного процесса при =0,2 и Т=3. (tр ≈12,5с)
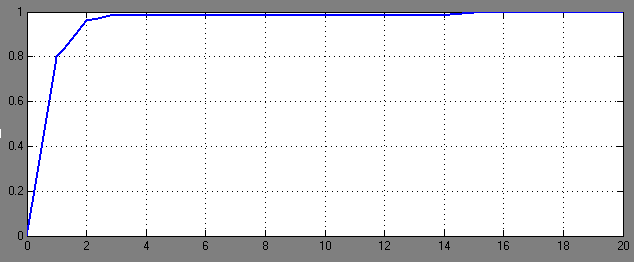
Рис.8-График переходного процесса при =0,2 и Т=14. (tр ≈1,9с)
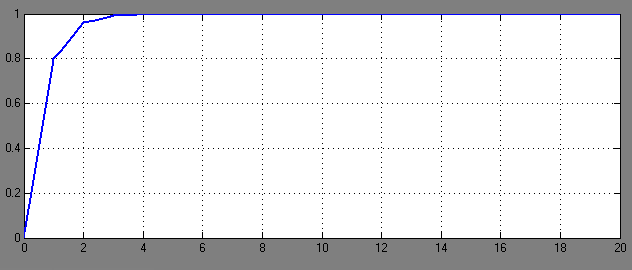
Рис.9-График переходного процесса при =0,6 и Т=0,4. (tр ≈4,8с)
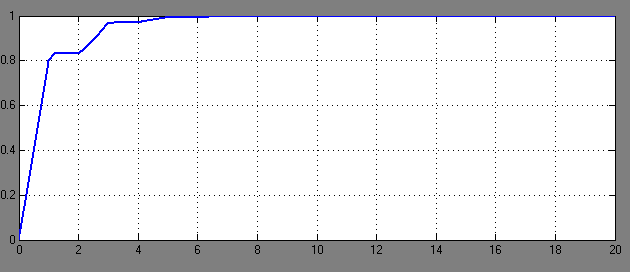
Рис.10-График переходного процесса при =0,6 и Т=2. (tр ≈4,8с)
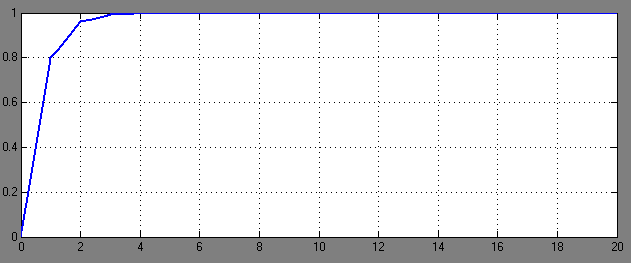
Рис.11-График переходного процесса при =0,6 и Т=7. (tр ≈1,9с)
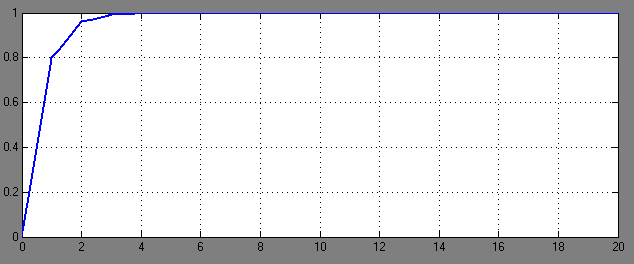
Рис.11-График переходного процесса при =0,9 и Т=0,1. (tр ≈2с)
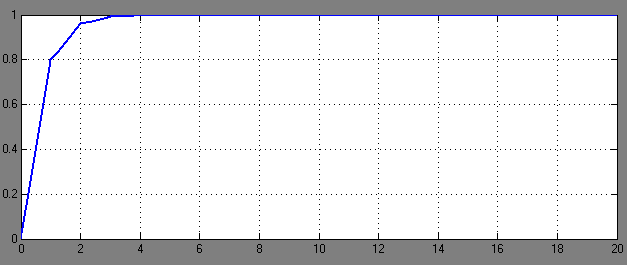
Рис.12-График переходного процесса при =0,9 и Т=1,5. (tр ≈2,1с)
Вывод: В ходе выполнения лабораторной работы были исследованы переходные процессы импульсной системы управления и изучили методы математического описания и анализа импульсных систем. По условию устойчивости было определены критическое значение периода следования и переходная функция рассматриваемой системы как функция параметров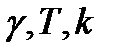 
и построен ее график. Графики переходных функци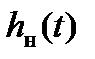й и 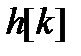практически одинаковы, что подтверждает правильность нахождения 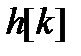. Время переходного процесса 
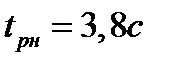, перерегулирование отсутствует. В результате можно сделать вывод, что при увеличении периода следования время переходного процесса уменьшается, но при достижении периода следования Ткрит время регулирования не опускается ниже tр=1.9с.