Динамика промышленных роботов.
Можно выделить две задачи:
• прямая;
• обратная.
i = 1, n 
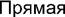
 q i q&i q&&i i = 1, n
q i q&i q&&i i = 1, n


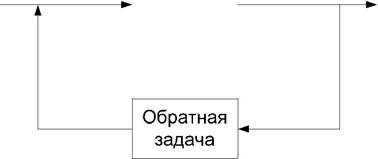


Рис. 33
Определение. Прямая задача динамики – задаются действующие в суставах моменты, необходимо определить обобщенные координаты суставов, их скорости и ускорения, иными словами необходимо определить закон изменения обобщенных координат. Данная задача используется при моделировании динамики промышленных роботов.
Определение. Обратная задача динамики – задается траектория движения манипулятора в виде законов изменения обобщенных координат, их скоростей и ускорений. Необходимо найти моменты, развиваемые валами двигателя при отработки заданной траектории.
Данная задача используется при построении алгоритма управления роботам с использованием динамической модели, при расчете и выборе силовых приборов и при моделировании динамики промышленных роботов.
Момент, развиваемый на валу двигателя можно записать следующим образом:
101
| n | •• | n | n | •• | ||||||||
| r | i = ∑H ij q j | + ∑∑h ijk q j q k | + G i | i = | 1, n | ( 155 ) | ||||||
| j= | j= | k=1 | ||||||||||
| 14243 | 1442443 | |||||||||||
| 1 | 2 | |||||||||||
В этом выражении: 1 – это инерционная составляющая момента. она показывает как влияет ускорение в j -ом суставе на момент i -ого сустава. 2
– составляющая, которая обусловлена действием центростремительных сил. G i - обусловлена силой тяжести.








