«Исследование автоколебаний методом гармонической линеаризации»

Дата: 2025-06-02; Просмотры: 6
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

МИНОБРНАУКИ РОССИИ

Федеральное государственное автономное образовательное

учреждение высшего образования

«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

ИНСТИТУТ РАДИОТЕХНИЧЕСКИХ СИСТЕМ И УПРАВЛЕНИЯ

КАФЕДРА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

 

 

 

 

Отчет

по лабораторной работе № 3

 

«Исследование автоколебаний методом гармонической линеаризации»

 

по курсу:

«Теория автоматического управления»

 

Выполнили:

Студенты группы РТбо3-7

Кошкальда Я.Ю.

Гладышев Д.А.

 

__________________

 

Проверил:

Ассистент каф. САУ

Денисенко Д. Ю.

 

__________________

 

 

Таганрог 2017 г.

Цель работы: Изучение метода гармонической линеаризации и исследование устойчивости нелинейных систем и их автоколебаний.

Таблица 1 – Исходные данные варианта.

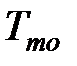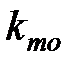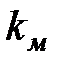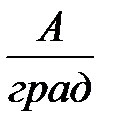
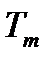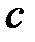
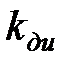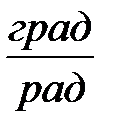
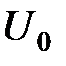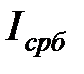Вариант , , , , , , В , А× 10-3
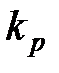
2 0,8 120 0,3 × 10-3 0,2 0,6 110 0,8 0,01

 

Динамика теплообменника (рассматриваемый объект управления) описывается уравнением:

;

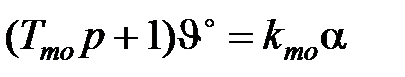где 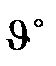– температура рабочей жидкости на выходе теплообменника; 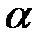– угол поворота вентиля, регулирующего подачу топлива; 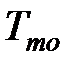и 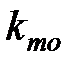– постоянная времени и коэффициент передачи теплообменника.

 

Уравнение измерителя рассогласования:

;

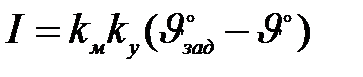где 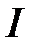– ток в обмотке реле; 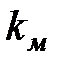– коэффициент передачи моста с термопарой; 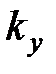– коэффициент усиления усилителя; 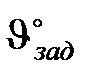– заданное значение температуры.

Уравнение двигателя:

,

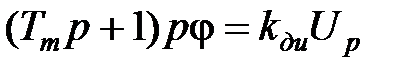где 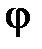– угол поворота вала двигателя; 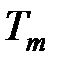и 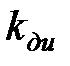– его постоянная времени и коэффициент передачи по напряжению.

Уравнение редуктора:

,

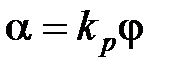где 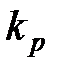– коэффициент передачи редуктора.

 

Выведем передаточные функции всех линейных элементов системы.

Передаточная функция измерителя рассогласования:

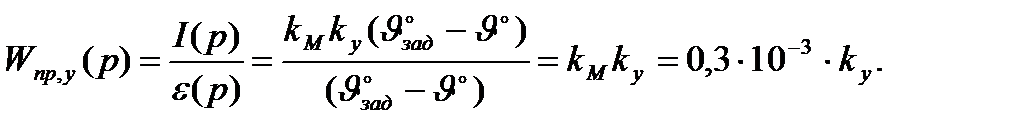
Передаточная функция двигателя:

 

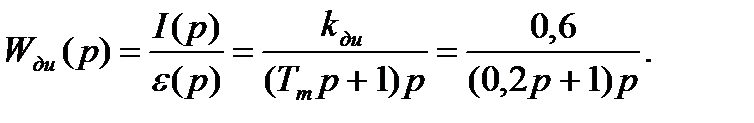
Передаточная функция редуктора:

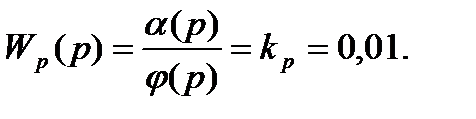
Передаточная функция объекта управления:

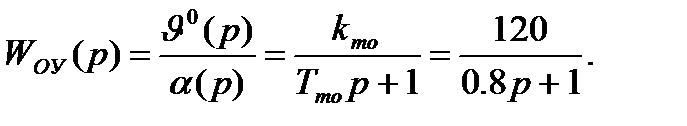
Рис.1. Структурная схема системы регулирования температуры

 

Приведем схему к стандартному виду:

Рис. 2. Структурная схема системы регулирования температуры в стандартном виде

 

Таким образом, передаточная функция линейной части описывается выражением:

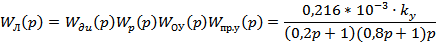
Коэффициент гармонической линеаризации нелинейности определяется выражением:

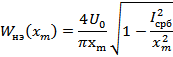
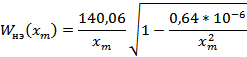
Для нахождения зависимости амплитуды автоколебаний 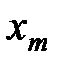от значения коэффициента усиления 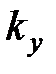воспользуемся критерием Гольдфарба:

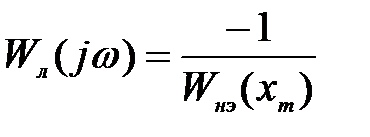
Так как 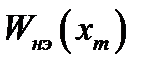- вещественная положительная функция, то пересечения годографов 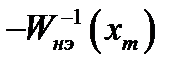и 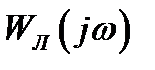возможны лишь на отрицательной вещественной полуоси, которую годограф 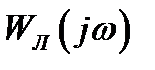пересекает при .

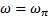Обе ветви годографа 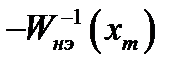совпадают с осью 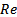, а точки 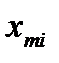совпадают с точкой ωπ. Переход с одной ветви на другую происходит в точке 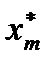. Путем дифференцирования 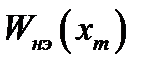по 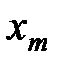устанавливаем, что максимум функции 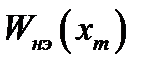или минимум модуля функции 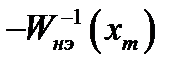достигается при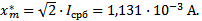

Найдем ωπ. Для этого перейдем в выражении передаточной функции линейного звена от 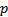к :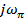

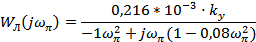
Очевидно, что в точке ωπ мнимая часть передаточной функции равна нулю:

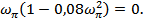
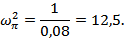
Подставив, в выражение критерия Гольдфарба найденное значение частоты получим:

 

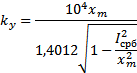
Для определения аналитическим путем значений коэффициента усиления 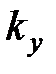, при которых автоколебания устойчивы, неустойчивы или отсутствуют, найдем критическое значение 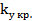, для которого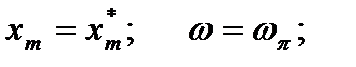

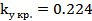
Отсюда следует, что при 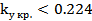автоколебания в системе отсутствуют, а при 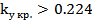возникают. В соответствии с критерием Найквиста точка 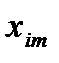, в которой пересекаются годографы 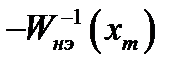и 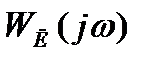, соответствует устойчивым автоколебаниям в том случае, когда, двигаясь от неё по кривой 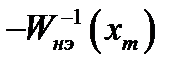в направлении роста амплитуды 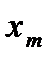, мы выходим за пределы контура, образованного годографом Найквиста. В противном случае автоколебания, соответствующие точке 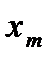будут неустойчивы.

 

Исследую систему на автоколебания при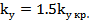

 

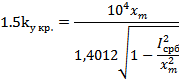
Полученные корни уравнения:

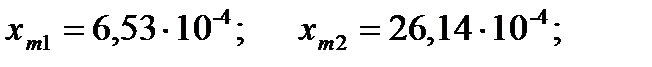
Устойчивыми будут автоколебания с частотой ω=2,5 и амплитудой 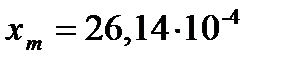, так как в этом случае, двигаясь от данной точки пересечения годографов по кривой 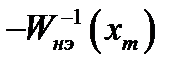в направлении роста амплитуды 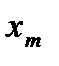, мы выходим за пределы контура, охватываемого годографом Найквиста.

Для проверки гипотезы фильтра найдем 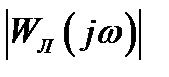при ω=ωπ и ω=2ωπ:

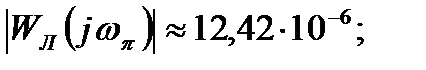
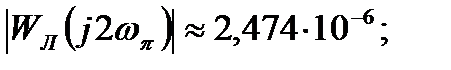
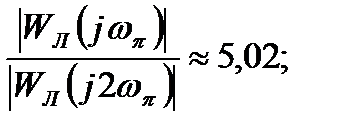
Как видно, амплитуда второй гармоники в 5,02 раза меньше амплитуды первой, поэтому гипотезу фильтра можно считать выполненной в первом приближении.

 

Структурная схема системы автоматического регулирования температуры в теплообменнике, набранная в Simulink :

График автоколебаний в системе при :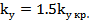

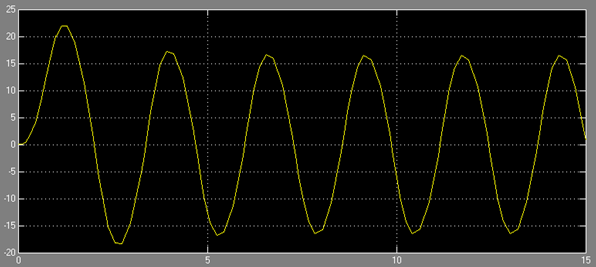
Как видно из графика, автоколебания имеют следующие параметры:

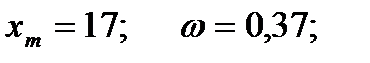(расчетные параметры: ω=2,5 и амплитудой )

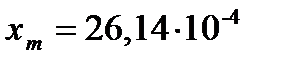Параметры не совпадают с результатами расчетов.

Исследование влияния коэффициента усиления 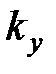на параметры автоколебаний в системе показало, что действительно автоколебания возникают при достижении некоторого критического значения коэффициента усиления 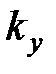. В дальнейшем увеличение коэффициента усиления оказывает незначительное влияния на параметры автоколебаний.

 

Вывод: В ходе выполнения данной работы был изучен метод гармонической линеаризации и произведено исследование устойчивости нелинейной системы и её автоколебаний. Также были найдены параметры установившихся автоколебаний для системы автоматического регулирования температуры в теплообменнике: амплитуду и частоту. Построили график зависимости амплитуды автоколебаний от значения коэффициента усиления 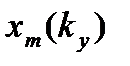. Аналитическим путем определили значение, которое определяет границы существования автоколебаний в системе.