Контрольное задание № 4.
Задача 1: Передаваемое сообщение состоит из 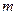 символов. Сообщение передается корректирующим кодом, который должен обнаружить и исправить ошибку в каждой кодовой комбинации. Определить значность, избыточность и относительное уменьшение пропускной способности канала для обнаруживающего и исправляющего кодов. Значения
символов. Сообщение передается корректирующим кодом, который должен обнаружить и исправить ошибку в каждой кодовой комбинации. Определить значность, избыточность и относительное уменьшение пропускной способности канала для обнаруживающего и исправляющего кодов. Значения 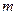 приведены в табл. 5.6.
приведены в табл. 5.6.
Таблица 5.6 Исходные данные
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Число символов 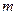
| 4 | 8 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
Задача 2: Значность кодовой комбинации содержит 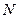 позиций. Определить число информационных и контрольных позиций. Значения
позиций. Определить число информационных и контрольных позиций. Значения 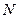 приведены в табл. 5.7.
приведены в табл. 5.7.
Таблица 5.7 Исходные данные
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
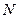
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Задача 3: Построить девятизначный корректирующий код для чисел, приведенных в табл. 5.8. Внести ошибку в шестую позицию кода. Найти проверочное число.
Таблица 5.8 Исходные данные
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 11 |
6. Теория передачи информации.
Сообщение перед поступлением в канал связи кодируется. При этом важно, чтобы скорость передачи сообщения по каналу связи равнялась скорости создания сообщения в кодирующем устройстве. Так как в реальном канале связи имеют место различные виды помех, то скорость передачи не будет соответствовать пропускной способности канала.
6.1 Передача информации по каналу связи без помех при различных видах кодирования.
В данном случае максимальное число символов, передаваемых по каналу связи будет определятся из выражения:
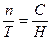 , (6.1)
, (6.1)
где 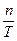 – количество символов, передаваемых в единицу времени, то есть
– количество символов, передаваемых в единицу времени, то есть 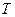 ;
;
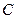 – пропускная способность канала;
– пропускная способность канала;
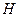 – энтропия источника передаваемых сообщений.
– энтропия источника передаваемых сообщений.
Если кодирование осуществляется с помощью время–импульсной модуляции (ВИМ), то есть временными интервалами, то они находятся из выражения:
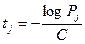 (6.2)
(6.2)
Средняя длительность элемента в сообщении для оптимального кода определяется по формуле:
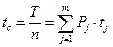 (6.3)
(6.3)
Для равномерного двоичного кода:
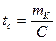 , (6.4)
, (6.4)
где 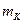 – число двоичных знаков в кодовой комбинации, которое, в свою очередь, определяется из выражения:
– число двоичных знаков в кодовой комбинации, которое, в свою очередь, определяется из выражения:
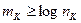 , (6.5)
, (6.5)
где 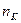 – число символов в сообщении.
– число символов в сообщении.
Следует отметить, что 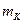 округляется ближайшим большим целым числом.
округляется ближайшим большим целым числом.
Зная среднее время по известным формулам можно определить скорость передачи информации.
6.2 Передача информации по каналу связи с помехами при различных видах кодирования.
Действие помех в канале связи может привести к потере части передаваемой информации. В связи с этим возникает вопрос о пропускной способности канала при наличии помех. Под пропускной способностью в этом случае понимается та максимальная скорость передачи информации при заданном уровне помех, при которой вероятность появления ошибки сколь угодно мала.
Пропускная способность канала определяется из выражения:
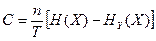 дв. ед/сек, (6.6)
дв. ед/сек, (6.6)
где 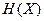 – энтропия источника информации;
– энтропия источника информации;
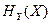 – энтропия неопределенности переданного сигнала
– энтропия неопределенности переданного сигнала 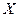 относительно принятого
относительно принятого 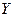 .
.
Из этой формулы следует, что пропускная способность уменьшается с увеличением 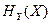 . Это означает, что для уменьшения действия помех необходимо вводить помехоустойчивое кодирование. Поскольку обычные шумовые помехи оказывают наибольший эффект на уровень (амплитуду) сигнала, все способы модуляции, в которых уровень не используется в качестве переносчика информации, являются помехоустойчивыми. В случае амплитудно–импульсной модуляции (АИМ) по мере повышения уровня помехи все большее число импульсов полезного сигнала теряется на фоне шума и, следовательно, помехоустойчивость канала падает.
. Это означает, что для уменьшения действия помех необходимо вводить помехоустойчивое кодирование. Поскольку обычные шумовые помехи оказывают наибольший эффект на уровень (амплитуду) сигнала, все способы модуляции, в которых уровень не используется в качестве переносчика информации, являются помехоустойчивыми. В случае амплитудно–импульсной модуляции (АИМ) по мере повышения уровня помехи все большее число импульсов полезного сигнала теряется на фоне шума и, следовательно, помехоустойчивость канала падает.
Передача информации в канале с кодоимпульсной модуляции (КИМ) осуществляется за счет определенного расположения импульсов на временных позициях кода. В идеальном случае параметры самих импульсов не несут информации и, следовательно, их искажение не вносит ошибок в передачу. Ошибки возникают лишь тогда, когда уровень помех настолько велик, что возможно образование на свободных позициях кода ложных импульсов и подавление полезных сигналов.
Пропускная способность канала при наличии помех будет определятся из выражения:
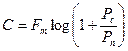 , (6.7)
, (6.7)
где 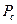 – мощность полезного сигнала;
– мощность полезного сигнала;
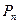 – мощность помехи;
– мощность помехи;
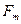 – наивысшая частота в спектре сигнала.
– наивысшая частота в спектре сигнала.
Используем формулу (6.7) для равномерно квантованного сигнала и равновероятного появления каждого уровня. В этом случае 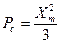 , где
, где 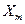 – максимальное значение уровня сигнала.
– максимальное значение уровня сигнала.
Дисперсия помехи 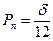 , где
, где 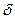 – шаг квантования.
– шаг квантования.
Подставляя эти значения в (6.7) получим:
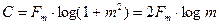 , (6.8)
, (6.8)
где 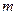 – число уровней квантования;
– число уровней квантования;
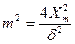
Мощность помехи в полосе частот полезного сигнала определяется из выражения:
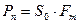 , (6.9)
, (6.9)
где 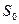 – спектральная плотность шума.
– спектральная плотность шума.
Определим скорость передачи информации по каналу связи при амплитудно–импульсной модуляции (АИМ). Шаг дискретизации по теореме Котельникова будет определятся:
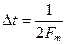 (6.10)
(6.10)
Обычно интервал между импульсами кодовой комбинации равен длительности импульса. Это означает, что ширина спектра импульса 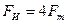 .
.
Так как все уровни сигнала равновероятны, то дисперсия сигнала (средняя мощность) будет равна:
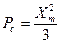 ( 6.11)
( 6.11)
или 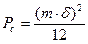 (6.12)
(6.12)
где 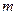 – количество уровней квантования;
– количество уровней квантования;
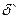 – шаг квантования.
– шаг квантования.
Для безошибочной передачи информации необходимо выбрать такой шаг квантования, при котором влияние шума было бы мало.
Вероятность ошибки в случае АИМ есть вероятность того, что уровень шума превысит половину шага квантования. Эта вероятность для нормального шума равна:
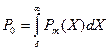 ,
,
где 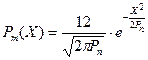 (6.13)
(6.13)
В связи с этим мощность помехи в полосе частот импульсов АИМ будет определятся:
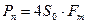 (6.14)
(6.14)
Из соотношений (6.11), (6.12) и (6.14) получим:
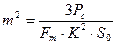 , (6.15)
, (6.15)
где 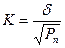 и выбирается из табл. 6.1, а
и выбирается из табл. 6.1, а 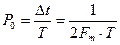 .
.
Таблица 6.1. Выбор коэфициентов.
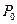
| 5·10-4 | 6,6·10-6 | 7·10-6 | 6·10-7 | 4·10-8 |
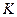
| 7 | 8 | 9 | 10 | 11 |
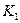
| 14 | 16 | 18 | 20 | 22 |
Скорость передачи по каналу связи будет равна:
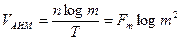 (6.16)
(6.16)
Избыточность кодов АИМ по отношению к идеальному кодированию может быть вычислена по формуле:
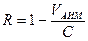 (6.17)
(6.17)
Определим скорость передачи информации по каналу при кодо–импульсной модуляции (КИМ). Для передачи одного значения сигнала 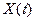 при использовании КИМ требуется передавать кодовую группу из
при использовании КИМ требуется передавать кодовую группу из 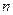 импульсов двух уровней (0 и 1). При этом общая длительность кодовых импульсов (с учетом интервалов между ними) должна быть равна длительности импуль са АИМ. Следовательно, ширина спектра импульса КИМ будет:
импульсов двух уровней (0 и 1). При этом общая длительность кодовых импульсов (с учетом интервалов между ними) должна быть равна длительности импуль са АИМ. Следовательно, ширина спектра импульса КИМ будет:
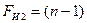
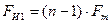 (6.18)
(6.18)
при условии, что прием импульсов КИМ производится приемником с пороговым устройством, всякий раз, когда уровень импульса 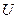 превышает порог
превышает порог 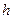 на малую величину
на малую величину 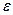 , то есть
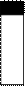
, то есть 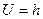 (рис. 6.1).
(рис. 6.1).
 | |||
 | |||
| |||
 | |||
Рисунок 6.1. сигнал с шумами.
Тогда вероятность ошибки равна вероятности превышения шумом порога 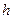 , то есть
, то есть 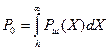 .
.
В табл. 6.1 приведены значения 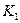 в зависимости от вероятности ошибки, причем
в зависимости от вероятности ошибки, причем 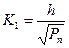 (6.19)
(6.19)
Мощность шума будет равна:
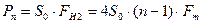 (6.20)
(6.20)
А средняя мощность полезного сигнала:
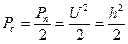 (6.21)
(6.21)
На основании выражений (6.19), (6.20), (6.21) получим:
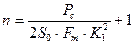 , (6.22)
, (6.22)
где 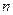 округляется до большего целого числа.
округляется до большего целого числа.
Скорость передачи по каналу с КИМ:
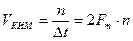 (6.23)
(6.23)
Избыточность кода КИМ по отношению к идеальному кодированию определяется из выражения:
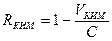 (6.24)
(6.24)








