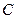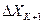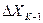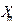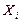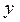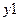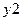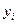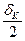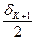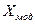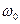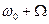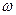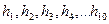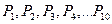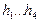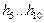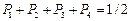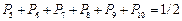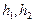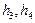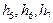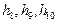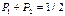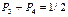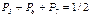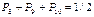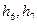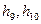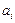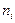2. Измерительные сигналы и их характеристики.
Сигнал – материальный носитель информации. Измерительным называют сигнал, обладающий информативным параметром. В процессе измерения информация должна быть выделена из входного сигнала оптимальным образом. Для этого необходимо знать свойства и особенности входного и выходного сигналов, их математические модели.
2.1 Классификация сигналов.
Сигналы классифицируются:
– по виду физического процесса: механические, электрические и магнитные, тепловые, акустические, световые и сигналы ионизирующих излучений;
– по характеру изменения во времени: детерминированные, квазидетерминированные, непрерывные или аналоговые, дискретизированные и случайные.
При изучении этого раздела следует уяснить особенности каждого вида сигналов и их дополнительную классификацию. Следует отметить, что квазидетерминированные сигналы подразделяются на элементарные и сложные.
К первому типу относятся: постоянный сигнал, идеальный единичный импульс и синусоидальный сигнал. При этом необходимо знать их математическую модель и информационные параметры.
К сложным квазидетерминированным сигналам относятся: полигармонический или периодический сигнал, периодический импульсный сигнал. При этом необходимо знать их информационные параметры и частотный спектр.
При рассмотрении переходных непериодических квазидетерминированных сигналов необходимо выделить: экспоненциальный сигнал, затухающий сигнал и прямоугольный сигнал. При изучении этих сигналов следует обратить внимание на их математическую модель и спектр
2.2 Случайные сигналы и их характеристики.
Виды случайных сигналов – нестационарные и стационарные, эргодические и неэргодические. При изучении случайных сигналов необходимо обратить внимание на их статистические параметры и характеристики, к которым относятся:
– среднее значение для данной реализации;
– среднеквадратическое значение;
– плотность распределения или дифференциальный закон распределения;
– дисперсия;
– функция распределения или интегральный закон распределения;
– автокорреляционная функция и коэффициент корреляции.
2.3 Основные формы сигналов, их метрологические характеристики и особенности с точки зрения измерения.
Сигналы подразделяются (рис. 2.1):

1) Сигнал непрерывный по размеру параметра
и во времени
 |
2) Сигнал дискретизированный во времени с
непрерывным по размеру параметром.
 |
3) Сигнал непрерывный во времени и кванто-
ванный по размеру.
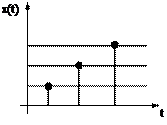 |
4) Сигнал дискретизированный во времени и
квантованный по размеру.
Рисунок 2.1. Формы сигналов.
При рассмотрении этих сигналов необходимо выделить особенности с точки зрения их измерения.
3. Преобразование сигналов в измерительных цепях.
Сигналы измерительной информации преобразуются в различных физических звеньях измерительных цепей. При этом характер преобразования определяется свойствами данных звеньев. Физические звенья и их функции подразделяются на линейные и нелинейные. Линейными называются звенья с параметрами, не зависящими от параметров преобразуемого сигнала. Нелинейными называются функции, удовлетворяющие условиям аддитивности и однородности.
3.1 Преобразование сигнала в линейных инерционных звеньях.
Особенностью инерционных звеньев является зависимость выходной величины не только от входной, но и от скорости ее изменения. В связи с этим важными динамическими характеристиками инерционных звеньев являются:
– переходная характеристика;
– передаточная функция;
– комплексная частотная характеристика;
– импульсная характеристика.
Рассмотрим эти характеристики на примере простейшей линейной RC-цепи (рис. 3.1).


|
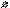 Данная цепь описывается дифференциаль
Данная цепь описывается дифференциаль 

 ным уравнением:
ным уравнением:
|
|
|
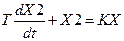 , (3.1)
, (3.1)

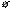
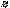
 где
где 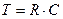 – постоянная времени;
– постоянная времени;
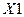 и
и 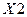 – соответственно входная и
– соответственно входная и
|
выходная величины.
Решение этого уравнения для нулевых начальных условий, то есть первая производная равна нулю, имеет вид:
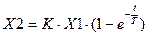 (3.2)
(3.2)
Если на вход этой цепи подать единичное воздействие 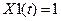 , то получим переходную характеристику линейной цепи:
, то получим переходную характеристику линейной цепи:
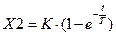 , (3.3)
, (3.3)
которая описывает процесс изменения во времени выходной величины, при скачкообразном изменении входной.
Для нахождения передаточной функции линейной цепи представим уравнение (3.1) в операторной форме:
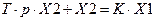 ,
,
отсюда 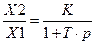 , то есть правая часть этого уравнения и будет определять передаточную функцию
, то есть правая часть этого уравнения и будет определять передаточную функцию
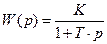 , (3.4)
, (3.4)
которая полностью определяет динамические свойства звена в момент времени подачи на вход измерительной величины.
Заменяя в выражении (3.4) оператор "p" на j w получим частотную характеристику линейной цепи:
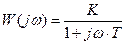 , (3.5)
, (3.5)
которая описывает изменение амплитуды и фазы гармонических сигналов при из прохождении через линейное звено.
Уравнение передаточной функции можно представить в виде:
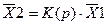 , (3.6)
, (3.6)
где 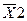 ,
, 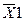 – соответственно изображение выходной и входной функций. Так как входной является единичная функция, то ее первая производная называется импульсной, то есть функцией Дирака, и может рассматриваться как математическое описание идеального импульса. Учитывая, что изображение производной равно единице, то выражение (3.6) примет вид:
– соответственно изображение выходной и входной функций. Так как входной является единичная функция, то ее первая производная называется импульсной, то есть функцией Дирака, и может рассматриваться как математическое описание идеального импульса. Учитывая, что изображение производной равно единице, то выражение (3.6) примет вид:
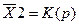 (3.7)
(3.7)
Оригинал этой функции называется импульсной характеристикой, описывающей закон изменения величины на выходе при подаче на вход линейного звена идеального импульса.
3.2 Квантование непрерывного сигнала по уровню.
Представление величины сигнала в виде конечного числа разрешенных уровней, отстоящих друг от друга на конечный интервал, называется квантованием по уровню. Если истинное мгновенное значение уровня сигнала находится внутри этого интервала, то вместо его передается ближайший разрешенный уровень. Если количество уровней квантования равно m, то передаваемый при этом сигнал будет содержать не более m различных значений.
Для того, чтобы обеспечить четкое разграничение принадлежности данного множества истинных мгновенных значений сигнала определенному уровню, вся область возможных значений сигнала делится на интервалы,
называемые шагами квантования. Оптимальным в смысле точности воспроизведения квантованного сигнала будет расположение уровня квантования в середине шага квантования.
Очевидно, при квантовании сигнала возникает ошибка в передаваемых значениях, обусловленная заменой истинного значения сигнала разрешенным уровнем. Таким образом, можно считать, что квантованный сигнал 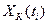 есть сумма истинного сигнала
есть сумма истинного сигнала 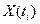 и ошибки
и ошибки 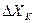 (рис. 3.2).
(рис. 3.2).
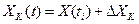 (3.8)
(3.8)
|
Вероятность появления уровня 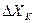 определяется вероятностью нахождения сигнала
определяется вероятностью нахождения сигнала 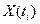 в интервале от
в интервале от 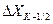 до
до 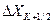 . Согласно рис. 3.2 ошибка
. Согласно рис. 3.2 ошибка 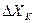 может изменяться в пределах от
может изменяться в пределах от 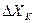 =
= 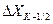 до
до 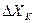 =
= 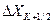 (3.8)
(3.8)
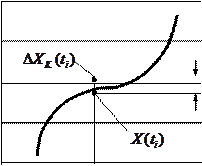 | ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
Рисунок 3.2. График квантового сигнала.
Так как значение 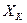 известно, то вероятность появления того или иного значения ошибки
известно, то вероятность появления того или иного значения ошибки 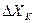 определяется вероятностью появления соответствующего значения сигнала
определяется вероятностью появления соответствующего значения сигнала 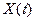 в момент ti. Для равномерного шага квантования дисперсия ошибки будет равна:
в момент ti. Для равномерного шага квантования дисперсия ошибки будет равна:
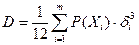 (3.9)
(3.9)
где 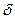 – шаг квантования,
– шаг квантования, 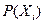 – функция плотности вероятности сигнала
– функция плотности вероятности сигнала 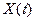 .
.
При равновероятном законе распределения случайного сигнала в диапазоне от 0 до 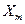 дисперсия при равномерном шаге квантования:
дисперсия при равномерном шаге квантования:
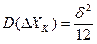 (3.10)
(3.10)
Среднеквадратическое отклонение погрешности:
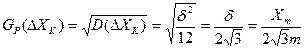 , (3.11)
, (3.11)
где 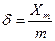 ,
, 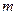 – число уровней квантования.
– число уровней квантования.
Для нормального, экспоненциального и треугольного законов распределения функции плотности вероятности дисперсия ошибки квантования определяется из выражения:
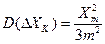 (3.12)
(3.12)
Выражение (3.9) показывает, что значение дисперсии зависти как от вида функции плотности вероятности 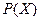 , так и от характера изменения шага квантования. Кроме того, из выражения (3.9) следует, что для уменьшения дисперсии ошибки квантования целесообразно менее вероятные значения сигнала квантовать с большим шагом, а более вероятные значения – с меньшим шагом.
, так и от характера изменения шага квантования. Кроме того, из выражения (3.9) следует, что для уменьшения дисперсии ошибки квантования целесообразно менее вероятные значения сигнала квантовать с большим шагом, а более вероятные значения – с меньшим шагом.
Рассмотрим задачу оптимального квантования, которая обеспечит минимальное значение дисперсии ошибки квантования, которую можно определить из выражения:
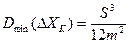 , (3.13)
, (3.13)
где 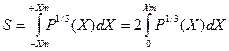 (3.14)
(3.14)
Любой 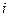 –ый уровень квантования можно найти как сумму шагов квантования по формуле:
–ый уровень квантования можно найти как сумму шагов квантования по формуле:
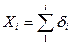 (3.15)
(3.15)
где шаг квантования 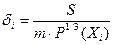 (3.16)
(3.16)
Подставляя выражение (3.16) в (3.15) получим:
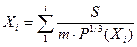 (3.17)
(3.17)
Это выражение можно приближенно заменить интегралом:
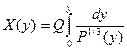 , (3.18)
, (3.18)
где 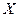 будет теперь непрерывной величиной, а постоянная
будет теперь непрерывной величиной, а постоянная 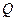 определяется из условия:
определяется из условия:
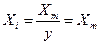 , то есть
, то есть
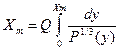 , откуда
, откуда 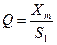 ,
,
где 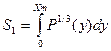 (3.19)
(3.19)
Подставляя значение 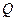 в выражение для
в выражение для 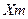 будем иметь:
будем иметь:
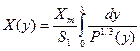 (3.20)
(3.20)
Формула (3.20) устанавливает функциональную связь между независимой переменной 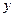 и переменной
и переменной 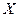 , которая в интервале от 0 до
, которая в интервале от 0 до 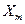 образует оптимальную шкалу квантования.
образует оптимальную шкалу квантования.
|
Так как независимая переменная 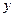 лежит в интервале от 0 до
лежит в интервале от 0 до 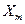 , то, разделив этот интервал на
, то, разделив этот интервал на 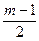 равных частей по кривой
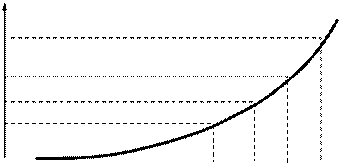
равных частей по кривой 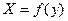 , удовлетворяющей формуле (3.20), находим значение уровней квантования
, удовлетворяющей формуле (3.20), находим значение уровней квантования 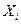 (рис. 3.3).
(рис. 3.3).
 | ||||||
| ||||||
| ||||||
| ||||||
| ||||||
 | ||||||||||||
| ||||||||||||
|
|
|
| |||||||||
Рисунок 3.3. Распределение уровней квантования.
После того, как найдены значения 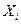 не представляет труда найти по формуле (3.16) шаги квантования
не представляет труда найти по формуле (3.16) шаги квантования 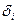 , и учитывая, что уровень квантования
, и учитывая, что уровень квантования 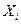 разбивает интервал
разбивает интервал 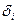 пополам, найти границы уровней.
пополам, найти границы уровней.
Для определения шагов квантования поступим следующим образом. Из рис. 3.4 имеем следующие соотношения:
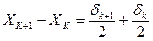 , (3.21)
, (3.21)
откуда 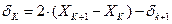 (3.22)
(3.22)
|
| |||||
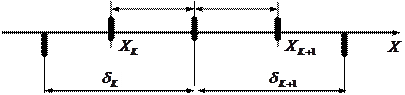 | ||||||
Рисунок 3.4. график определения шагов квантования.
При практических расчетах целесообразно по формуле (3.16) определить значение 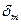 :
:
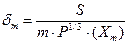
Определение дальнейших 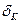 целесообразно производить по формуле (3.22).
целесообразно производить по формуле (3.22).
Дисперсия ошибки оптимального квантования для экспоненциального закона распределения функции плотности вероятности определяется из выражения:
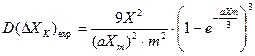 (3.23)
(3.23)
Зная уровни и шаги квантования, можно построить оптимальную шкалу квантования, которая в общем виде изображена на рис. 5.3.
 |
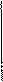





|
|
|
| ||||||||||||
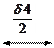 | |||||||||||||||
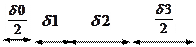 | |||||||||||||||
Рисунок 5.3. Оптимальная шкала квантования.
Задача : Непрерывный случайный сигнал, изменяющийся в диапазоне от 0 до 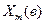 равномерно квантован 5–ю уровнями, включая и нулевой. Найти
равномерно квантован 5–ю уровнями, включая и нулевой. Найти 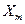 непрерывного сигнала, если дисперсия ошибки квантования
непрерывного сигнала, если дисперсия ошибки квантования 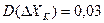 , а закон распределения функции плотности вероятности равновероятный.
, а закон распределения функции плотности вероятности равновероятный.
Решение: Для равномерного закона 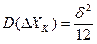 , отсюда
, отсюда 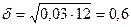 ,
, 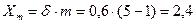 в.
в.
Контрольное задание № 2:
Задача 1: Непрерывный случайный сигнал, изменяющийся в диапазоне от 0 до 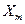 , равномерно квантован
, равномерно квантован 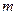 уровнями. Найти дисперсию погрешности квантования и среднеквадратичное отклонение
уровнями. Найти дисперсию погрешности квантования и среднеквадратичное отклонение 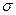 , если закон распределения функции плотности вероятности равновероятный, экспоненциальный и нормальный. Параметры сигнала приведены в табл. 3.1.
, если закон распределения функции плотности вероятности равновероятный, экспоненциальный и нормальный. Параметры сигнала приведены в табл. 3.1.
Таблица 3.1. Исходные данные.
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
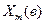
| 3 | 6 | 3 | 6 | 8 | 8 | 4 | 4 | 5 | 5 |
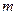
| 5 | 5 | 4 | 6 | 10 | 8 | 5 | 4 | 10 | 8 |
Задача 2: Истинное значение непрерывного случайного сигнала 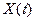 , изменяющегося от 0 до
, изменяющегося от 0 до 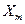 в момент времени
в момент времени 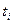 равно
равно 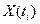 . Сигнал квантован с шагом 0,5 в. Найти уровень квантованного сигнала, если математическое ожидание
. Сигнал квантован с шагом 0,5 в. Найти уровень квантованного сигнала, если математическое ожидание 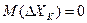 . Найти относительную погрешность определения уровня квантованного сигнала
. Найти относительную погрешность определения уровня квантованного сигнала 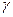 . Данные взять из табл. 3.2.
. Данные взять из табл. 3.2.
Таблица 3.2. Исходные данные.
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
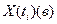
| 0,2 | 0,3 | 0,4 | 0,6 | 0,7 | 0,9 | 1,2 | 1,5 | 1,8 | 2,8 |
Задача 3: Сигнал 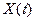 характеризуется одномерной плотностью вероятности вида
характеризуется одномерной плотностью вероятности вида 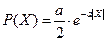 и изменяющийся в диапазоне от
и изменяющийся в диапазоне от 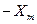 до
до 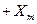 .
.
1) Требуется построить оптимальную шкалу квантования с числом уровней 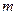 , если максимальное значение сигнала
, если максимальное значение сигнала 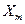 . Параметры сигнала приведены в табл. 3.3.
. Параметры сигнала приведены в табл. 3.3.
Таблица 3.3. Исходные данные.
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
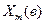
| 3 | 6 | 9 | 9 | 6 | 3 | 12 | 12 | 1,5 | 3 |
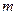
| 9 | 9 | 7 | 11 | 7 | 7 | 9 | 11 | 5 | 5 |
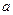
| 1 | 0,5 | 1/3 | 1/3 | 0,5 | 1 | 1/4 | 1/4 | 2 | 1 |
2) Построить график функции плотности вероятности.
3) Определить дисперсию ошибки оптимального и равномерного квантования.
Примечание: Поскольку сигнал изменяется симметрично относительно своего нулевого значения, достаточно ограничиться расчетом только положительных значений уровней квантования.
3.3 Дискретизация сигналов.
В дискретизированном сигнале каждое значение строго привязано к определенному моменту времени. Промежуток времени между соседними моментами дискретизации называется шагом дискретизации. При значительно малом шаге дискретизации увеличивается время передачи информации и усложняется аппаратурная реализация. При большом шаге теряется информация. Выбор оптимального шага дискретизации основывается на теореме отсчетов Котельникова, которая гласит: если функция 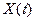 не содержит частот
не содержит частот 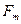 герц, то она полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на
герц, то она полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на 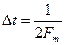 . Смысл теоремы заключается в том, что функция не может существенно изменить свое значение за время меньше, чем половина периода наивысшей частоты
. Смысл теоремы заключается в том, что функция не может существенно изменить свое значение за время меньше, чем половина периода наивысшей частоты 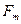 .
.
Для аналитического задания функции 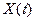 с помощью ее значений в моменты отсчета используется вспомогательная функция вида:
с помощью ее значений в моменты отсчета используется вспомогательная функция вида:
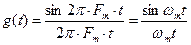
Свойства этой функции позволяют непрерывный сигнал 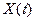 представить в виде дискретизированного:
представить в виде дискретизированного:
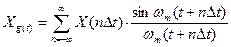 ,
,
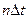 – отсчетные точки.
– отсчетные точки.
Теорема Котельникова предназначена для сигналов с ограниченным спектром, а реальные сигналы всегда ограничены во времени и имеют бесконечный спектр. Однако, с достаточной для практики точностью можно ограничить спектр частотой 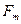 . В этом случае для полного задания сигнала
. В этом случае для полного задания сигнала 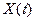 длительностью
длительностью 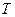 общее число отсчетов
общее число отсчетов 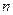 можно определить из выражения:
можно определить из выражения:
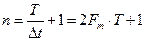
При 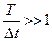
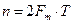 , при этом дискретизированный сигнал примет вид :
, при этом дискретизированный сигнал примет вид :
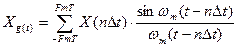
Задача: Длительность непрерывного сигнала 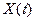 конечна и равна
конечна и равна 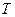 , а полоса частот от 0 до
, а полоса частот от 0 до 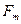 . Определить число шагов дискретизации, если
. Определить число шагов дискретизации, если 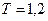 сек,
сек, 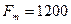 Гц.
Гц.
Решение: По теореме Котельникова
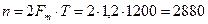
В дискретизированном сигнале отсутствуют промежуточные значения, поэтому после его приема производят обратную операцию, то есть восстановление. Для восстановления непрерывного сигнала из дискретизированного также применяется теорема Котельникова и аппроксимация степенными полиномами.
Теорема Котельникова: если функция 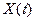 обладает спектром с граничной частотой
обладает спектром с граничной частотой 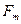 , дискретизирована циклически с периодом
, дискретизирована циклически с периодом 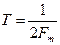 , то она может быть восстановлена по этой совокупности ее мгновенных значений без погрешности, то есть:
, то она может быть восстановлена по этой совокупности ее мгновенных значений без погрешности, то есть:
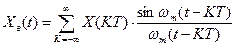 ,
,
где 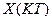 – мгновенное значение сигнала, взятое с интервалом
– мгновенное значение сигнала, взятое с интервалом 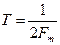 .
.
При восстановлении сигнала степенными полиномами используется линейная аппроксимация. При изучении этого вопроса следует выделить:
– ступенчатую аппроксимацию;
– кусочно-линейную аппроксимацию;
– параболическую аппроксимацию.
Кроме того, следует обратить внимание на приведенную погрешность аппроксимации и ее связь с частотой дискретизации.
4. Модуляция и детектирование сигнала.
Модуляцией называют преобразование информационного сигнала в новый с заданным законом изменения. Ее используют для передачи, преобразования и обработки информационного измерительного сигнала, если его передача затруднена. Модуляция реализуется путем взаимодействия двух сигналов – модулирующего исходного сигнала 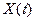 , содержащего информацию, и несущего
, содержащего информацию, и несущего 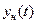 .
.
В несущем гармоническом сигнале 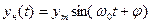 могут модулироваться амплитуда
могут модулироваться амплитуда 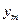 , частота
, частота 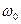 и фаза
и фаза 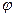 . Соответственно различают амплитудную, частотную и фазовую модуляции. Если в качестве несущего сигнала используется последовательность прямоугольных импульсов, то различают следующие виды импульсной модуляции:
. Соответственно различают амплитудную, частотную и фазовую модуляции. Если в качестве несущего сигнала используется последовательность прямоугольных импульсов, то различают следующие виды импульсной модуляции:
– амплитудно-импульсную (АИМ);
– частотно-импульсную (ЧИМ);
– фазо-импульсную (ФИМ);
– широтно-импульсную (ШИМ);
– кодо-импульсную (КИМ);
Во всех видах импульсной модуляции последовательность прямоугольных импульсов изменяется по закону модулирующего сигнала.
4.1 Амплитудная модуляция и детектирование.
Амплитудно-модулированный сигнал содержит три спектральные частотные составляющие с частотами 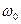 ,
, 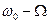 ,
, 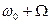 и имеет вид:
и имеет вид:
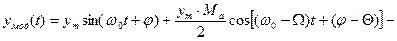
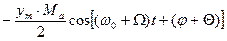 (4.1)
(4.1)
где 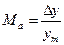 – коэффициент модуляции;
– коэффициент модуляции;
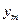 – амплитуда несущего сигнала;
– амплитуда несущего сигнала;
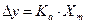 – девиация амплитуды;
– девиация амплитуды;
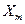 – максимальное значение модулирующего сигнала;
– максимальное значение модулирующего сигнала;
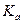 – коэффициент преобразования модулятора.
– коэффициент преобразования модулятора.
Исходя из вышеизложенного, следует, что 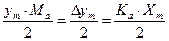
Спектр амплитудно-модулированного сигнала представлен на рис. 4.1.
|

 | |||||||||
|
|
| |||||||
| |||||||||
Рисунок 4.1.Спектр модулированного сигнала.
Информация в модулированном сигнале содержится в боковой гармонике.
Если амплитуда несущего сигнала равняется нулю, то такой вид модуляции называют балансной.
Детектирование – это процесс выделения полезного информативного сигнала, то есть боковых гармоник.
4.2 Частотная модуляция и детектирование.
При этом виде модуляции изменяется частота несущего сигнала по закону модулирующего 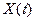 . Частотно-модулированный сигнал имеет вид:
. Частотно-модулированный сигнал имеет вид:
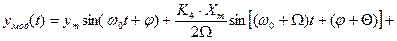
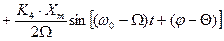 , (4.2)
, (4.2)
где 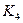 – коэффициент преобразования модулятора;
– коэффициент преобразования модулятора;
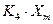 – девиация частоты;
– девиация частоты;
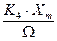 – коэффициент частотной модуляции.
– коэффициент частотной модуляции.
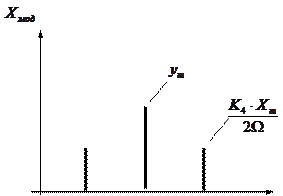
Спектр частотно-модулированного сигнал представлен на рис. 4.2.
 | |||||||||
|
|
| |||||||
| |||||||||
Рисунок 4.2. Спектр частично-модулированного сигнала.
Информативным параметром модулированного сигнала является гармоника с боковой частотой 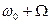 или
или 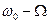 .
.
Если информативным параметром 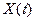 является его амплитуда
является его амплитуда 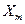 , то информативный параметр выходного сигнала – амплитуда гармоники:
, то информативный параметр выходного сигнала – амплитуда гармоники:
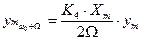 или
или 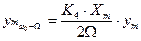
Частотный детектор состоит из линейной измерительной системы, преобразующей частотную модуляцию в амплитудную, и амплитудного детектора.
4.3 Фазовая модуляция и детектирование.
Для осуществления фазовой модуляции на высокочастотное несущее колебание, нужно воздействовать низкочастотным сигналом 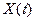 . В этом случае фазо-модулированный сигнал примет вид:
. В этом случае фазо-модулированный сигнал примет вид:
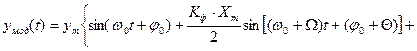
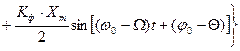 (4.3)
(4.3)
где 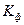 – коэффициент преобразования фазового модулятора;
– коэффициент преобразования фазового модулятора;
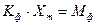 – коэффициент фазовой модуляции.
– коэффициент фазовой модуляции.
Амплитуды боковых гармоник фазо-модулированного сигнала в отличии от частотной модуляции не зависят от частоты, то есть:
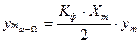 или
или 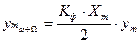
Для детектирования модулированного сигнала с быстрым изменением фазы применяют детекторы с опорным сигналом.
5. Коды и кодирование в измерении.
Данный раздел предусматривает согласно программы изучение и построение только оптимального и корректирующего кодов.
5.1 Оптимальные или эффективные коды.
Информация, передаваемая по каналу связи состоит из набора кодовых комбинаций-букв или чисел. Каждая буква, в свою очередь, кодируется комбинацией символов или знаков кода.
Для передачи по каналу связи каждого символа необходимо затратить время 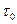 , поэтому, чем больше символов необходимо для кодирования каждой буквы, тем длиннее их комбинация, тем больше необходимо затратить времени при передаче.
, поэтому, чем больше символов необходимо для кодирования каждой буквы, тем длиннее их комбинация, тем больше необходимо затратить времени при передаче.
Среднее время передачи независимых кодовых комбинаций:
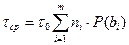 , (5.1)
, (5.1)
где 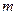 – число кодовых комбинаций;
– число кодовых комбинаций;
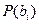 – вероятность данной кодовой комбинации
– вероятность данной кодовой комбинации 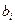 ;
;
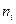 – число символов в кодовой комбинации.
– число символов в кодовой комбинации.
Скорость передачи информации по каналу:
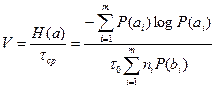 , (5.2)
, (5.2)
где 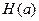 – энтропия источника, передаваемого информацию.
– энтропия источника, передаваемого информацию.
Для увеличения скорости передачи необходимо снижать время 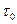 , однако его минимальное значение ограничено шириной полосы пропускания канала
, однако его минимальное значение ограничено шириной полосы пропускания канала 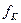 :
:
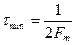
Исходя из этого, необходимы и другие меры для повышения скорости передачи информации. Одной из таких мер является статистическое согласование источника информации и кода. В выражении (5.2) вероятности элементов сообщений 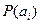 при безошибочном кодировании равны вероятности соответствующих кодовых комбинаций
при безошибочном кодировании равны вероятности соответствующих кодовых комбинаций 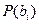 . Скорость передачи будет наибольшей, если выполняется условие:
. Скорость передачи будет наибольшей, если выполняется условие:
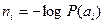 (5.3)
(5.3)
В этом случае скорость передачи информации достигнет максимального значения, равного пропускной способности (С) канала связи с двоичными символами кода:
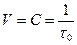
Выполнение условий статистического согласования
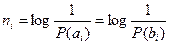 означает, что более вероятные элементы сообщения должны кодироваться более короткими комбинациями символов с меньшим числом
означает, что более вероятные элементы сообщения должны кодироваться более короткими комбинациями символов с меньшим числом 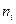 , менее вероятные элементы – с большим. Коды, удовлетворяющие этому требованию, называются оптимальными или эффективными (код Шенона – Фано).
, менее вероятные элементы – с большим. Коды, удовлетворяющие этому требованию, называются оптимальными или эффективными (код Шенона – Фано).
Если кодирование осуществляется временными интервалами, а пропускная способность канала задана, то построение оптимального кода сводится к нахождению этих временных интервалов 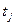 :
:
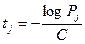 (5.4)
(5.4)
Для случая, когда длительности знаков "0" и "1" одинаковы, способ оптимального кодирования заключается в следующем. Из выражения (5.4) следует, что при равенстве длительности знаков "0" и "1" должны быть одинаковы и их вероятности. Это обстоятельство сразу определяет способ разбиения символов сообщения на группы, очевидно, суммарные вероятности, в которых должны быть одинаковы. Итак, в результате разбиения 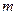 символов сообщения на две группы: в первой из них мы будем иметь
символов сообщения на две группы: в первой из них мы будем иметь 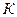 символов с суммарной вероятностью около 1/2, а во второй
символов с суммарной вероятностью около 1/2, а во второй 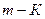 символов, также с суммарной вероятностью, близкой к 1/2. Одна группа будет закодирована "0", другая – "1". Далее каждая из групп разбивается на две подгруппы. При этом первая подгруппа будет закодирована "00", а вторая – "01". Совершенно такая же операция производится во второй группе. Описанные операции показаны в таблице 5.1 для 10 символов. Описанная процедура построения кода продолжается до тех пор, пока разбиения не приведут к числу подгрупп, равных числу символов
символов, также с суммарной вероятностью, близкой к 1/2. Одна группа будет закодирована "0", другая – "1". Далее каждая из групп разбивается на две подгруппы. При этом первая подгруппа будет закодирована "00", а вторая – "01". Совершенно такая же операция производится во второй группе. Описанные операции показаны в таблице 5.1 для 10 символов. Описанная процедура построения кода продолжается до тех пор, пока разбиения не приведут к числу подгрупп, равных числу символов 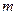 .
.
Таблица 5.1. Способ разбиения символов сообщения.
| Символы |
| |||||||||
| Вероятности |
| |||||||||
| Группы | 1 | 2 | ||||||||
| Символы |
|
| ||||||||
| Вероятности |
|
| ||||||||
| Код группы | 0 | 1 | ||||||||
| Подгруппы | 1 | 2 | 3 | 4 | ||||||
| Символы |
|
|
|
| ||||||
| Вероятности |
|
|
|
| ||||||
| Код подгруппы | 00 | 01 | 10 | 11 | ||||||
| Подгруппы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Символы | 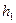
| 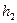
| 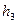
| 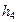
| 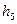
|
| 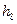
|
| ||
| Вероятности | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | ||
| Код подгруппы | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | ||
| Подгруппы |
| 1 | 2 | 3 | 4 | 5 | ||||
| Символы |
| 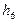
| 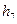
| 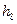
| 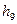
| 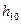
| ||||
| Вероятности |
| 1/16 | 1/16 | 1/16 | 1/16 | |||||
| Код подгруппы |
| 1010 | 1011 | 1100 | 1111 | |||||
Рассмотрим принцип построения оптимального кода. Пусть источник информации вырабатывает сообщения 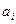 с вероятностью
с вероятностью 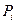 (табл. 5.2). Необходимо построить оптимальный код.
(табл. 5.2). Необходимо построить оптимальный код.
Таблица 5.2 Построение оптимального кода
|
|
| Группа | Комбинация |
| Двоичный код | ||
| 1 | 2 | 3 | |||||
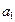
| 0,5 | 0 | 0 | 1 | 00 | ||
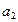
| 0,25 | 1 | 0 | 10 | 2 | 01 | |
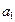
| 0,125 | 1 | 1 | 0 | 110 | 3 | 10 |
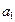
| 0,125 | 1 | 1 | 1 | 111 | 3 | 11 |
Определим скорость передачи информации для оптимального и равномерного двоичного кодов по формуле (5.2).
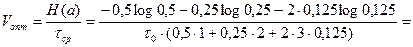
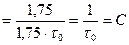 .
.
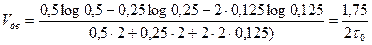 .
.
Отношение скоростей:
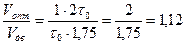 раза
раза
Контрольное задание № 3:
Задача 1: Сообщение формируется из 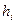 символов, вероятность
символов, вероятность 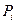 которых приведена в табл. 5.3. Построить оптимальный код.
которых приведена в табл. 5.3. Построить оптимальный код.
Таблица 5.3. Вероятности появления символов.
 Вариант Вариант
| 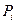 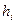
| 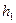
| 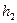
| 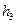
| 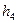
| 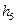
| 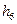
| 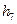
| 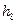
| 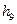
|
| 0 | 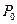
| 0,3 | 0,2 | 0,15 | 0,1 | 0,1 | 0,05 | 0,05 | 0,03 | 0,02 |
| 1 | 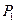
| 0,2 | 0,2 | 0,15 | 0,1 | 0,1 | 0,1 | 0,05 | 0,05 | 0,05 |
| 2 | 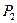
| 0,35 | 0,25 | 0,15 | 0,1 | 0,05 | 0,03 | 0,02 | 0,03 | 0,02 |
| 3 | 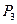
| 0,5 | 0,25 | 0,15 | 0,1 | |||||
| 4 | 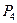
| 0,3 | 0,15 | 0,2 | 0,1 | 0,1 | 0,05 | |||
| 5 | 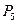
| 0,15 | 0,15 | 0,15 | 0,15 | 0,15 | 0,15 | 0,1 | ||
| 6 | 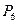
| 0,2 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 |
| 7 | 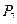
| 0,4 | 0,15 | 0,15 | 0,1 | 0,05 | 0,05 | 0,05 | 0,03 | 0,02 |
| 8 | 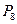
| 0,3 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,05 | 0,05 |
| 9 | 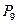
| 0,45 | 0,3 | 0,15 | 0,05 | 0,05 |
Примечание: число символов в сообщении определяется заданной вероятностью.
Задача 2: По каналу связи необходимо передать сообщение, закодированное оптимальным кодом. Сообщение содержит 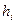 символов с вероятностями
символов с вероятностями 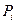 , заданными в табл. 5.4. Определить скорость передачи сообщения, если пропускная способность канала
, заданными в табл. 5.4. Определить скорость передачи сообщения, если пропускная способность канала 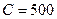 дв. ед/сек.
дв. ед/сек.
Таблица 5.4. Вероятности появления символов.
 Вариант Вариант
| 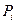 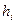
| 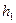
| 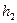
| 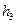
| 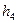
| 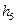
|
| 0 | 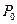
| 0,5 | 0,2 | 0,2 | 0,05 | 0,05 |
| 1 | 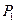
| 0,4 | 0,3 | 0,1 | 0,1 | 0,1 |
| 2 | 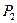
| 0,4 | 0,2 | 0,2 | 0,1 | 0,1 |
| 3 | 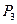
| 0,5 | 0,15 | 0,15 | 0,1 | 0,1 |
| 4 | 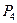
| 0,3 | 0,2 | 0,15 | 0,15 | 0,2 |
| 5 | 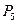
| 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
| 6 | 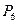
| 0,2 | 0,2 | 0,3 | 0,15 | 0,15 |
| 7 | 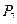
| 0,1 | 0,2 | 0,15 | 0,15 | 0,4 |
| 8 | 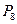
| 0,3 | 0,3 | 0,3 | 0,05 | 0,05 |
| 9 | 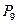
| 0,25 | 0,15 | 0,4 | 0,1 | 0,1 |
5.2 Корректирующие коды.
Пропускная способность канала связи уменьшается при наличии помех. Это означает, что для преодоления действия помех необходимо вводить в кодирующее устройство более сложный способ кодирования. Одним из способов решения этой задачи является применение корректирующих кодов, то есть кодов с помощью которых обнаруживаются и исправляются ошибки от действия помех. Их принцип основан на избыточности элементов кода. Свойства этих кодов наглядно объясняются геометрическими представлениями, введенными Хэммингом.
Хэмминг изобразил кодовую группу в 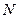 – мерном пространстве в виде
– мерном пространстве в виде 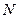 – мерного куба, каждое ребро которого отвечает позиции (разряду) двоичного знака в кодовой группе (рис. 5.1, для
– мерного куба, каждое ребро которого отвечает позиции (разряду) двоичного знака в кодовой группе (рис. 5.1, для 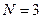 )
)
|
|
|
|
|
|
|
|
|
|









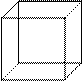 Вершины куба соответствуют всем возможным комбинациям чисел данной группы. При этом Хэмминг ввел метрику пространства, задав расстояние между двумя вершинами куба равным в геометрической интерпритации наименьшему числу ребер куба. Так, например, расстояние между точками 010 и 111 равно двум, так как попасть можно по двум ребрам, обведенным пунктиром.
Вершины куба соответствуют всем возможным комбинациям чисел данной группы. При этом Хэмминг ввел метрику пространства, задав расстояние между двумя вершинами куба равным в геометрической интерпритации наименьшему числу ребер куба. Так, например, расстояние между точками 010 и 111 равно двум, так как попасть можно по двум ребрам, обведенным пунктиром.
|
|
Таким образом для 3-х мерного пространства будем иметь:
– кодовые точки, расстояние между которыми равно трем (000 и 111, или 100 и 011, или 010 и 101, или 110 и 001 );
– кодовые точки, расстояние между которыми равно двум (000, 101, 011 и 110, или 001, 100, 010 и 111);
– кодовые точки, расстояние между которыми равно единице (000, 001, 010, 011, 100, 101, 110 и 111).
Одиночные ошибки возникают в коде из-за действий помех, если один из символов кодовой группы искажается таким образом, что вместо "1" появляется "0" и наоборот. Ошибки такого рода могут быть обнаружены в коде, у которого расстояние между кодоввыми комбинациями равно "1" 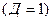 , так как при этом одна кодовая точка переходит в другую. Если же расстояние между кодовыми комбинациями равно двум, то появление одиночной ошибки переводит кодовую точку в соседнюю, не используемую для передачи, и ошибка обнаруживается. Практически обнаружение ошибки производится путем проверки кодовой комбинации на четность или на нечетность.
, так как при этом одна кодовая точка переходит в другую. Если же расстояние между кодовыми комбинациями равно двум, то появление одиночной ошибки переводит кодовую точку в соседнюю, не используемую для передачи, и ошибка обнаруживается. Практически обнаружение ошибки производится путем проверки кодовой комбинации на четность или на нечетность.
Одиночная ошибкаможет быть исправлена, если расстояние между кодовыми комбинациями увеличить до трех, тогда ошибочная комбинация будет отстоять от правильной на единицу, а от остальных, не менее чем на две, что и позволяет заменить ошибочную комбинацию на правильную, то есть исправить ошибку.
5.2.1 Обнаружение одиночной ошибки 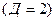 .
.
Если в 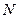 – мерном кубе имеется
– мерном кубе имеется 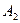 точек, отстоящих друг от друга на 2 единицы, то они будут разрешенными для передачи. Для определения разрешенных точек
точек, отстоящих друг от друга на 2 единицы, то они будут разрешенными для передачи. Для определения разрешенных точек 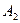 представим
представим 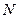 – мерный куб в виде двух
– мерный куб в виде двух 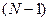 –мерных кубов. Следовательно, в пространстве Хэмминга этот куб будет иметь
–мерных кубов. Следовательно, в пространстве Хэмминга этот куб будет иметь 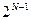 вершин и содержать два квадрата из
вершин и содержать два квадрата из 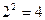 вершин. Следовательно, в
вершин. Следовательно, в 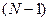 – мерном кубе будет не более
– мерном кубе будет не более 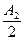 разрешенных кодовых точек. По аналогии в
разрешенных кодовых точек. По аналогии в 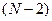 – мерном кубе будет не более
– мерном кубе будет не более 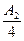 разрешенных кодовых точек.
разрешенных кодовых точек.
Для 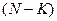 – мерного куба число разрешенных кодовых точек будет равно
– мерного куба число разрешенных кодовых точек будет равно 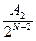 , где
, где 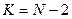 . Так как в квадрате имеется 2 точки с
. Так как в квадрате имеется 2 точки с 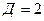 , то
, то 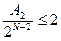 , откуда
, откуда 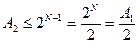 (5.5)
(5.5)
где 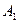 – общее число комбинаций в коде.
– общее число комбинаций в коде.
Таким образом, для обнаружения одиночной ошибки в 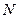 – значном коде используется для передачи только половина кодовых комбинаций
– значном коде используется для передачи только половина кодовых комбинаций 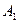 .
.
Избыточность кодовых комбинаций 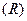 определится из выражения:
определится из выражения:
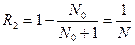 , (5.6)
, (5.6)
где 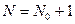 – значимость кода.
– значимость кода.
Относительное уменьшение пропускной способности канала:
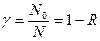 , (5.7)
, (5.7)
где 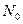 – число разрешенных кодовых комбинаций.
– число разрешенных кодовых комбинаций.
5.2.2 Обнаружение и исправление одиночной ошибки 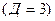 .
.
Число разрешенных кодовых точек 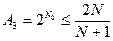 , тогда
, тогда 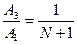 (5.8)
(5.8)
Относительное уменьшение пропускной способности канала:
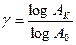 , (5.9)
, (5.9)
где 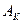 – число разрешенных кодовых групп в корректирующем коде;
– число разрешенных кодовых групп в корректирующем коде;
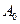 – общее число кодовых групп в корректирующем коде.
– общее число кодовых групп в корректирующем коде.
Так как 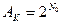 ,
, 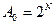 , то
, то
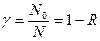 (5.10)
(5.10)
Избыточность кода 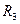 определится из выражения:
определится из выражения:
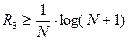 (5.11)
(5.11)
Задача: Передаваемое сообщение состоит из 16 символов. Сообщение передается корректирующим кодом, который должен обнаружить и исправить одиночную ошибку в каждой кодовой комбинации. Определить значность, избыточность и относительное уменьшение пропускной способности канала для обнаруживающего и исправляющего кодов.
Решение: Для обнаруживающего кода:
значность 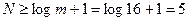
По формуле (5.6) определим избыточность :

Относительное уменьшение пропускной способности канала определим из выражения (5.7):
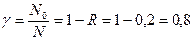
Для исправляющего кода:
Согласно (5.8) 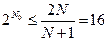 , где
, где 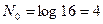 . Решив это неравенство, получим
. Решив это неравенство, получим 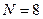 .
.
По формуле (5.11) 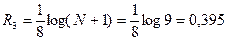 .
.
По формуле (5.10) находим 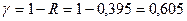 .
.
5.2.3 Методика построения корректирующего кода.
Корректирующий код должен содержать 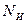 – информационных и
– информационных и 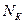 – контролирующих позиций, то есть
– контролирующих позиций, то есть 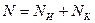 .
.
Исходя из этого, на первом этапе необходимо определить 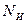 и
и 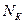 из выражения
из выражения 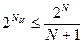 , где
, где 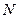 – значность кода.
– значность кода.
Например, для 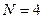 число информационных позиций
число информационных позиций 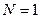 , так как
, так как 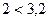 , а число контролируемых позиций
, а число контролируемых позиций 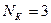 .
.
На втором этапе определяем позиции кодовых групп, которые необходимо проверить при каждой из 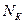 проверок. Для примера рассмотрим 10 – значный код и пронумируем позиции кода слева направо от 1 до 10, записав номера позиций в двоичных числах:
проверок. Для примера рассмотрим 10 – значный код и пронумируем позиции кода слева направо от 1 до 10, записав номера позиций в двоичных числах:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 |
Подсчитаем, какие позиции имеют в своих двоичных номерах "1" в младшем разряде, во втором, третьем и четвертом разрядах. Результаты заносим в табл. 5.5.
Таблица 5.5. Результаты подсчётов.
| № проверки | № разряда | Проверяемые позиции |
| 1 | 1 | 1 3 5 7 9 |
| 2 | 2 | 1 3 6 7 10 |
| 3 | 3 | 4 5 6 7 |
| 4 | 4 | 8 9 10 |
Из таблицы видно, что в качестве контролируемых необходимо выбрать 1, 2, 4, 8 позиции, так как они позволяют проверить четность во всех разрядах. При этом позиции 3, 5, 6, 7, 9, 10 будут информационными, то есть 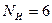 ,
, 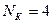 .
.
Схема кодовой группы примет вид:
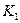
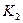
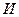
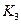
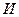
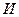
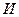
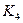
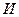
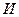
где 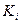 – контрольные позиции;
– контрольные позиции;
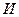 – информационные позиции.
– информационные позиции.
По данной схеме можно построить код для любого числа. Так, например, для числа 10 кодовая группа примет вид:
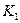
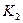 0
0 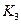 0 1 0
0 1 0 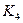 1 0
1 0
Проверяем на четность все позиции (табл. 5.5), в результате чего находим значения 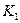 ,
, 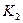 ,
, 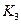 ,
, 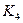 . В нашем случае
. В нашем случае 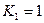 ,
, 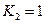 ,
, 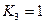 ,
, 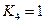
Таким образом, кодовая группа для числа 10 примет вид:
1 1 0 1 0 1 0 1 1 0
Если в результате помехи в кодовой группе числа 10 вместо "0" на 7 позиции появится "1", то есть в результате искажения кодовая группа будет принята в виде:
1 1 0 1 0 1 1 1 1 0
В результате первой проверки на четность ошибка обнаруживается, следовательно в младшем разряде проверочного числа запишем "1". При второй проверке на четность ошибка обнаруживается. Поэтому во втором разряде проверочного числа запишем "1". Третья проверка вновь дает нечетность и проверочное число становится 111. Четвертая проверка ошибки не обнаруживает и проверочное число примет вид 0111. Так как это двоичное число соответствует десятичному "7", ошибка произошла на седьмой позиции. Она будет исправлена, если на этой позиции заменить "1" на "0".