4. Модуляция и детектирование сигнала
4.1 Амплитудная модуляция и детектирование ………………..........................................….21
4.2 Частотная модуляция и детектирование ……………............................................……..….21
4.3 Фазовая модуляция и детектирование ……………….….........................................…..…22
5. Коды и кодирование в измерении
5.1 Оптимальные или эффективные коды ……...........................................…….………….....23
5.2 Корректирующие коды ………………………...………….........................................….…26
5.2.1 Обнаружение одиночной ошибки ……...…………...........................................…...26
5.2.2 Обнаружение и исправление одиночной ошибки ….........................................…27
5.2.3 Методика построения корректирующего кода ............................................……..…28
6. Теория передачи информации
6.1 Передача информации по каналу связи без помех при различных видах
кодирования ……………………….…................................................................................……...30
6.2 Передача информации по каналу связи с помехами при различных видах
кодирования …………………….…………...................................................................................30
7. Методы повышения точности измерительных приборов и преобразователей
7.1 Классификация методов коррекции погрешностей ……….................................................34
7.2 Структурные методы автоматической коррекции погрешностей измерительных
приборов и преобразователей.....................................................................................................34
Литература ………..……………………….……………………….........................................……35
Введение
Курс "Теоретические основы измерительных и информационных технологий" рассматривает способы и средства получения, передачи, обработки и целенаправленного использования количественной и качественной информации о свойствах и характеристиках физических объектов с целью их изучения и управления.
При изучении данного курса необходимо последовательно рассмотреть следующие разделы:
– основные понятия информации и информационной теории измерений;
– энтропия и количество информации взаимосвязанных источников сигналов;
– теория передачи информации;
– каналы связи и их характеристики;
– передачи информации по каналу связи без помех и при их наличии;
Для более полного усвоения материала, а так же выполнения курсовой работы, необходимо выполнить контрольные задания, прилагаемые к каждому разделу, опираясь при этом на примеры выполненных расчётов, приведённых в методических указаниях.
1. Основные понятия информации и информационной
теории измерения.
При изучении этого раздела необходимо усвоить следующие определения:
– понятие информации – это сообщения, сведения, знания, которые могут характеризоваться различными аспектами: объемом, новизной, содержательностью, полезностью и т. д.;
– измерительная информация – количественные сведения о свойстве объекта, получаемые опытным путем с помощью измерительных средств. Она может быть представлена в виде числа, кода, диаграммы и т. д.;
– количество измерительной информации – численная мера степени уменьшения неопределенности количественной оценки свойства объекта, получаемой путем измерения;
– математические меры информации – логарифмическая и вероятностная.
1.1 Логарифмическая мера.
При измерении величина может принимать 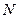 значений. Чем больше
значений. Чем больше 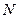 , тем труднее определить ее истинное (действительное) значение. Следовательно, исходная неопределенность возрастает с увеличением
, тем труднее определить ее истинное (действительное) значение. Следовательно, исходная неопределенность возрастает с увеличением 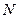 . Исходная неопределенность до измерения определяется логарифмической функцией от
. Исходная неопределенность до измерения определяется логарифмической функцией от 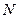 , то есть:
, то есть:
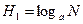
Неопределенность после измерения уменьшается и определяется из выражения:
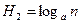 ,
,
где 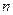 – число возможных значений величины после измерения, характеризующее его погрешность.
– число возможных значений величины после измерения, характеризующее его погрешность.
В таком случае количество информации, полученной в результате измерения, определится из выражения:
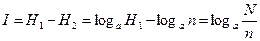 (1.1)
(1.1)
Единицы неопределенности определяются выбором основания логарифма. При 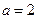 – двоичная единица информации или бит, которую мы в дальнейшем будем использовать. В связи с этим при дальнейших расчетах основание логарифма будем опускать.
– двоичная единица информации или бит, которую мы в дальнейшем будем использовать. В связи с этим при дальнейших расчетах основание логарифма будем опускать.
1.2 Вероятностная мера.
Пусть по каналу связи передается сообщение, состоящее из 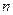 символов, при этом вероятность появления
символов, при этом вероятность появления 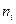 символа равна
символа равна 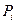 . В таком случае количество информации, полученной в результате приема этого сообщения, будет равно:
. В таком случае количество информации, полученной в результате приема этого сообщения, будет равно:
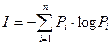 (1.2)
(1.2)
Эта мера неопределенности получила название энтропия, которую в дальнейшем будем обозначать 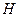 , то есть
, то есть 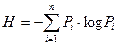 (1.3)
(1.3)
Исходя из этого, энтропия – это количество информации, которое необходимо для устранения степени неопределенности.
Свойства энтропии как математической меры неопределенности:
– энтропия является непрерывной положительной функцией аргументов 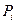 ;
;
– при заданном числе возможных исходов 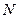 энтропия принимает максимальное значение, когда все они равновероятны, то есть:
энтропия принимает максимальное значение, когда все они равновероятны, то есть:
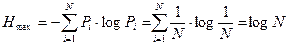
Задача 1: Шахматная фигура на доске является системой с 64 равновозможными состояниями, вероятность каждого из которых равна 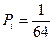 . Энтропия такой системы:
. Энтропия такой системы: 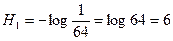 бит.
бит.
Найти энтропию и количество информации для сообщений:
– фигура стоит на одной из горизонтальных линий. Так как каждая клетка находится на горизонтальных линиях, то новой информации нет;
– фигура стоит на черном поле, 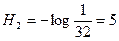 бит. Такое сообщение принесло информацию
бит. Такое сообщение принесло информацию 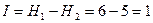 бит;
бит;
– фигура стоит на одной из угловых клеток, 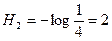 бит.
бит. 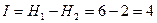 бит;
бит;
– фигура находится на клетке 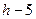 .
. 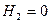 , так как положение фигуры достоверно,
, так как положение фигуры достоверно, 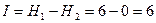 бит.
бит.
1.3 Исходная энтропия подлежащей измерению непрерывной величины.
Определим энтропию непрерывной величины, подлежащей измерению с погрешностью 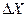 . При этом диапазон значений непрерывной величины
. При этом диапазон значений непрерывной величины 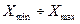 , разобьем на
, разобьем на 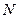 интервалов, то есть
интервалов, то есть 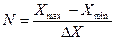 .
.
Если задана плотность вероятности значений величины 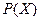 , то энтропию можно найти из выражения:
, то энтропию можно найти из выражения:
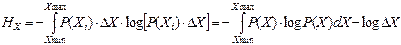 (1.4)
(1.4)
Слагаемое 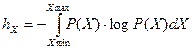 – называется дифференциальной энтропией, которая зависит только от вероятностей значений измеряемой величины.
– называется дифференциальной энтропией, которая зависит только от вероятностей значений измеряемой величины.
Для равномерного закона распределения значений непрерывной величины:
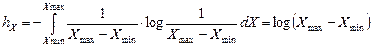 (1.5)
(1.5)
Полная энтропия при заданной погрешности 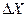 примет вид:
примет вид:
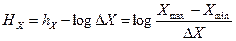 (1.6)
(1.6)
Для нормального закона распределения значений непрерывной величины:
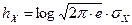 ,
,
где 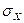 – среднее квадратическое отклонение значений измеряемой величины
– среднее квадратическое отклонение значений измеряемой величины 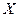 .
.
Полная энтропия с учетом погрешности равна:
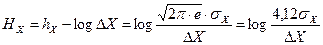 (1.7)
(1.7)
1.4 Остаточная энтропия значений величины после измерения.
Исходная неопределенность знания о значении величины не может быть нижена до нуля в результате измерения, так как имеется погрешность. При этом область неопределенности сужается от 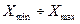 до интервала
до интервала 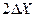 , расположенного симметрично относительно полученного результата
, расположенного симметрично относительно полученного результата 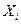 . (Рис. 1.1)
. (Рис. 1.1)
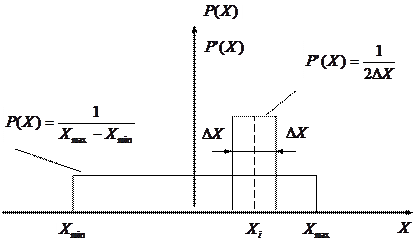 |
Рисунок 1.1. Области неопределённости.
Остаточная дифференциальная энтропия непрерывной величины будет иметь вид:
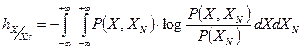 , (1.8)
, (1.8)
где 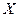 – измеряемая величина;
– измеряемая величина;
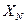 – результат измерения.
– результат измерения.
Полная остаточная энтропия после измерения определяется разностью:
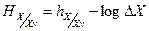 (1.9)
(1.9)
Для нормального закона распределения дифференциальная остаточная энтропия:
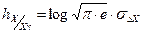 , (1.10)
, (1.10)
где 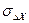 – среднеквадратическое отклонение погрешности.
– среднеквадратическое отклонение погрешности.
Когда погрешность распределена по равномерному закону в интервале 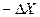 до
до 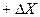 , дифференциальная остаточная энтропия равна:
, дифференциальная остаточная энтропия равна:
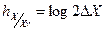 (1.11)
(1.11)
Задача 2: Амперметр, класс точности которого равен 1, имеет шкалу от 1 до 5 А. Допустимая погрешность 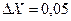 А.
А.
Найти энтропию показания этого прибора при условии, что любое показание в диапазоне равновероятно.
Решение: Зона допуска измеряемого сигнала составляет 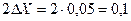 А.. Энтропия показания этого прибора:
А.. Энтропия показания этого прибора:
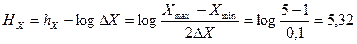 бит.
бит.
Задача 3: Амперметр с верхним пределом измерения 100 А имеет цену деления 2 А/дел. Рабочая часть шкалы начинается с 20 А. Практически отсчет показаний такого прибора можно производить с точностью до 1 А.
Найти информационную способность прибора
Решение: Определяем число возможных комбинаций 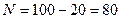 . Определяем информационную способность прибора:
. Определяем информационную способность прибора:
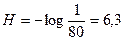 бит.
бит.
1.5 Энтропия и количество информации взаимосвязанных объектов.
Взаимосвязь может определяться различными факторами:
– источник коррелированного сигнала. В этом случае вырабатываемый сигнал содержит взаимосвязанные символы, которые будут характеризоваться условной вероятностью 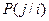 того, что после появления символа
того, что после появления символа 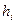 будет следовать символ
будет следовать символ 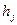 ;
;
– два параллельно работающих взаимосвязанных источника. Здесь вырабатываемые сигналы содержат также взаимосвязанные символы, но принадлежащие различным источникам;
– источник и приемник, связанные каналом с помехами. Наличие помех не дает полной уверенности в правильности приема символов. Можно лишь с некоторой вероятностью 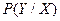 утверждать, что принятый символ
утверждать, что принятый символ 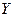 есть переданный символ
есть переданный символ 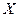 .
.
Рассмотрим соотношения, определяющие энтропии взаимосвязанных объектов.
Для источника квантованных сообщений с 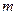 символами, где
символами, где 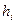 символов имеют вероятности появления
символов имеют вероятности появления 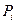 , взаимосвязь символов задается условной вероятностью
, взаимосвязь символов задается условной вероятностью 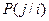 , то есть вероятностью того, что после появления символа
, то есть вероятностью того, что после появления символа 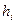 появится символ
появится символ 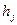 . В этом случае энтропию для всех символов по отношению к символу
. В этом случае энтропию для всех символов по отношению к символу 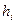 можно определить как:
можно определить как:
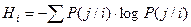
Общая условная энтропия может быть определена как математическое ожидание энтропии 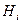 :
:
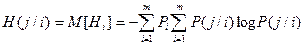 (1.12)
(1.12)
Задача 4: Сигнал формируется в виде двоичного кода с вероятностями появления символов 1 и 0, равными соответственно 0,6 и 0,4. Появление любого из символов взаимосвязаны условными вероятностями:
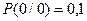 – вероятность того, что после 0 опять будет 0;
– вероятность того, что после 0 опять будет 0;
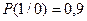 – вероятность того, что после 0 будет 1;
– вероятность того, что после 0 будет 1;
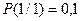 – вероятность того, что после 1 опять будет 1;
– вероятность того, что после 1 опять будет 1;
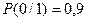 – вероятность того, что после 1 будет 0.
– вероятность того, что после 1 будет 0.
Применяя формулу (1.12) и учитывая, что 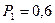 и
и 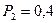 , получим:
, получим:
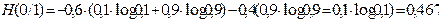 бит.
бит.
Для двух параллельно работающих взаимосвязанных источников, вырабатывающих дискретные сигналы 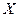 и
и 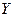 будут иметь место соотношения:
будут иметь место соотношения:
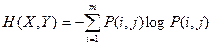 (1.13)
(1.13)
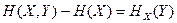 (1.14)
(1.14)
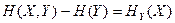 (1.15)
(1.15)
По аналогии можно записать соотношения для дифференциальной совместной энтропии:
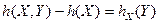 (1.16)
(1.16)
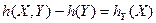 (1.17)
(1.17)
Энтропия квантованного сообщения с нормальным законом распределения может быть определена:
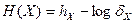 , где
, где 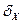 – шаг квантования
– шаг квантования
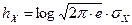 , тогда
, тогда
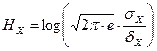 (1.18)
(1.18)
Для случая взаимосвязанных сигналов, имеющих значения 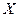 и
и 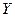 , имеющих нормальный закон распределения:
, имеющих нормальный закон распределения:
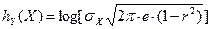 (1.19)
(1.19)
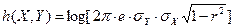 , (1.20)
, (1.20)
где 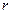 – коэффициент корреляции
– коэффициент корреляции
По аналогии энтропия квантованного сигнала:
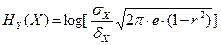 (1.21)
(1.21)
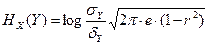 (1.22)
(1.22)
Но так как 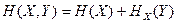 , то используя формулы (1.21) и (1.22) будем иметь:
, то используя формулы (1.21) и (1.22) будем иметь:
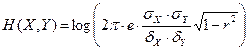 (1.23)
(1.23)
Задача 5: Система стабилизации платформы имеет два дискретных датчика А и В, измеряющих углы 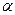 и
и 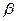 во взаимно перпендикулярных плоскостях (Рис. 1.2)
во взаимно перпендикулярных плоскостях (Рис. 1.2)
|
|
|
|


 Сигналы
Сигналы 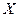 и
и 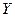 с датчиков А и В поступают на вычислительное устройство (ВУ). Датчики имеют число уровней квантования
с датчиков А и В поступают на вычислительное устройство (ВУ). Датчики имеют число уровней квантования 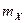 и
и 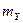 .
.
Требуется определить:
– 

|
совместную энтропию сигналов 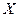 и
и 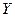 ;
;
– энтропию источников (датчиков А и В) при их независимой работе;
|
– условные энтропии сигналов 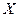 и
и 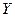 при совместной работе датчиков;
при совместной работе датчиков;
– количество информации, поступающей в ВУ за время работы Т.
Система характеризуется данными:
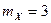 ;
; 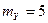 ;
; 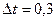 сек;
сек; 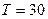 сек.
сек.
Совместные вероятности 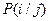 заданы в табл. 1.1.
заданы в табл. 1.1.
Таблица 1.1. Совместные вероятности

| 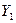
| 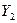
| 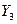
| 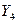
| 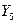
|
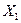
| 0,12 | 0,10 | 0,08 | 0,05 | 0,03 |
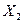
| 0,02 | 0,04 | 0,12 | 0,04 | 0,02 |
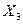
| 0,03 | 0,05 | 0,08 | 0,10 | 0,12 |
Для определения совместной энтропии 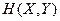 воспользуемся формулой (1.13):
воспользуемся формулой (1.13):
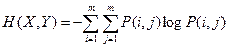
Используя таблицу вероятностей будем иметь:
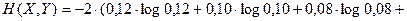
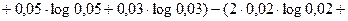
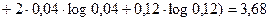 дв. ед.
дв. ед.
Энтропии 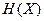 и
и 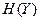 источников при их независимой работе определяются по общей формуле:
источников при их независимой работе определяются по общей формуле: 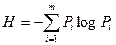 .
.
Для вычисления вероятностей появления сигналов 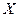 и
и 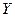 воспользуемся соотношениями:
воспользуемся соотношениями:
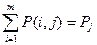 ,
, 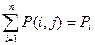
В таком случае для получения значений вероятностей сигнала 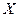 необходимо просуммировать строки таблицы 1.1, а для
необходимо просуммировать строки таблицы 1.1, а для 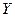 – просуммировать столбцы таблицы 1.1. Результаты расчетов приведены в табл. 1.2 и 1.3.
– просуммировать столбцы таблицы 1.1. Результаты расчетов приведены в табл. 1.2 и 1.3.
Таблица 1.2. Вероятности сигнала Х. Таблица 1.3. Вероятности сигнала У.
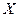
| 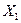
| 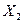
| 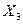
| 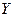
| 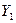
| 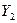
| 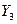
| 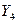
| 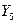
| |
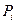
| 0,38 | 0,24 | 0,38 | 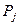
| 0,17 | 0,19 | 0,28 | 0,19 | 0,17 |
Расчет энтропии дает следующие результаты:
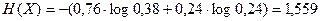 дв. ед.
дв. ед.
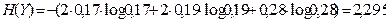 дв. ед.
дв. ед.
Условные энтропии определим по формулам:
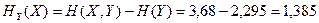 дв. ед.
дв. ед.
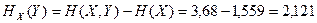 дв. ед.
дв. ед.
Легко увидеть, что энтропия источника А при работе В и энтропия источника В при работе А меньше энтропий этих источников, работающих независимо, на величину:
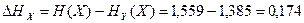 дв. ед.
дв. ед.
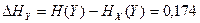 дв. ед.
дв. ед.
Количество информации, поступающее в вычислительное устройство за все время работы, определим по формуле:
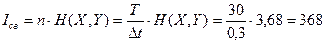 дв. ед.
дв. ед.
При независимой работе источников А и В в вычислительное устройство поступило бы количество информации:
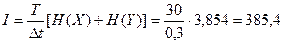 дв. ед.
дв. ед.
Для более полного усвоения данного раздела необходимо выполнить контрольное задание №1.
Контрольное задание № 1:
Задача 1: В системе регулирования частоты вращения электродвигателя задающее воздействие 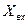 в виде электрического напряжения имеет
в виде электрического напряжения имеет 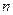 независимых дискретных значений с шагом квантования
независимых дискретных значений с шагом квантования 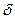 , вероятности появления которых распределены по двустороннему экспоненциальному закону с функцией плотности
, вероятности появления которых распределены по двустороннему экспоненциальному закону с функцией плотности 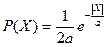 . Данные для
. Данные для 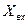 ,
, 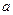 и
и 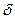 взять из табл. 1.4.
взять из табл. 1.4.
Таблица 1.4. Исходные данные.
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Задающее воздействие 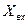 , (В) , (В)
| 1,6 | 1,4 | 1,2 | 1,6 | 1,4 | 1,2 | 2,4 | 2,1 | 1,8 | 1,5 |
Шаг квантования 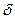 , (В) , (В)
| 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,3 | 0,3 | 0,3 | 0,3 |
Коэффициент 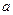
| 0,5 | 0,5 | 0,5 | 1 | 1 | 1 | 0,5 | 0,5 | 0,5 | 0,5 |
Число уровней 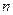
| 17 | 15 | 13 | 17 | 15 | 13 | 17 | 15 | 13 | 11 |
Задача 2: Амперметр имеет рабочую шкалу от 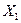 до
до 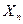 А. Допустимая погрешность
А. Допустимая погрешность 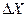 . По прибору получен результат измерения 4,2 А.
. По прибору получен результат измерения 4,2 А.
Найти дифференциальную энтропию и количество полученной информации, полагая закон распределения погрешности нормальным, имеющим среднее квадратическое отклонение 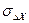 , равное
, равное 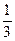 допустимой погрешности. Данные приведены в табл. 1.5.
допустимой погрешности. Данные приведены в табл. 1.5.
Таблица 1.5. Исходные данные.
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Диапазон 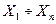 , (А) , (А)
| 1-5 | 0-5 | 1-6 | 1-7 | 0-6 | 0-7 | 1-8 | 1-9 | 1-10 | 0-10 |
Дополнительная погрешность 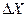 , (А) , (А)
| 0,06 | 0,06 | 0,06 | 0,09 | 0,06 | 0,06 | 0,06 | 0,09 | 0,09 | 0,09 |
Задача 3: Устройство вырабатывает случайный сигнал 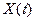 с одномерным нормальным распределением и корреляционной функцией вида
с одномерным нормальным распределением и корреляционной функцией вида 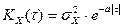 . Данные сигнала:
. Данные сигнала: 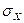 – амплитудное значение (В);
– амплитудное значение (В); 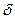 – шаг квантования;
– шаг квантования; 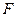 – наивысшая частота в спектре сигнала. Данные приведены в табл. 1.6.
– наивысшая частота в спектре сигнала. Данные приведены в табл. 1.6.
Определить энтропию сигнала при наличии и отсутствии корреляции.
Таблица 1.6. Исходные данные.
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
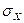 , (В) , (В)
| 10 | 12 | 10 | 8 | 6 | 12 | 5 | 12 | 8 | 10 |
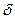 , (В) , (В)
| 0,6 | 0,6 | 0,5 | 0,4 | 0,2 | 0,4 | 0,2 | 0,3 | 0,2 | 0,25 |
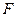 , (Гц) , (Гц)
| 25 | 25 | 15 | 25 | 25 | 20 | 25 | 25 | 10 | 25 |
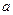 , (Гц) , (Гц)
| 50 | 25 | 30 | 25 | 50 | 40 | 50 | 25 | 20 | 50 |
При решении данной задачи необходимо ознакомиться с характеристиками случайных сигналов, в частности, с автокорреляционной функцией и коэффициентом корреляции. Необходимо помнить, что в данном случае коррелируют предыдущий сигнал с последующим. Кроме того, необходимо ознакомиться с дискретизацией непрерывных сигналов, в частности, с теоремой отсчетов Котельникова.








