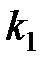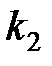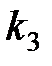Федеральное государственное автономное образовательное
МИНОБРНАУКИ РОССИИ
Федеральное государственное автономное образовательное
учреждение высшего образования
«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ РАДИОТЕХНИЧЕСКИХ СИСТЕМ И УПРАВЛЕНИЯ
КАФЕДРА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ


Отчет
по лабораторной работе № 2
«Исследование нелинейной системы методом фазовой плоскости»
по курсу:
«Теория автоматического управления»
Выполнили:
Студенты группы РТбо3-7
Кошкальда Я.Ю.
Гладышев Д.А.
Проверил:
Ассистент каф. САУ
Денисенко Д. Ю.
__________________
Таганрог 2017 г.
Цель работы: Изучение метода фазовой плоскости. Исследование влияния гибкой обратной связи на переходные процессы нелинейных систем управления второго порядка.
Выполнение:
| № варианта | Параметры нелинейности | | | | | ||
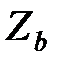
| b | ||||||
| 2 | 4,5 | 2,0 | 15 | 1 | 10 | 0,8 | |
Схема 1.
Для 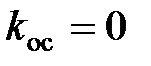 :
:
При построении фазового портрета входной сигнал системы обычно полагают равным нулю, т.е. в рассматриваемом случае 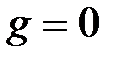 . Поэтому уравнения элементов системы, в соответствии со структурной схемой, имеют вид:
. Поэтому уравнения элементов системы, в соответствии со структурной схемой, имеют вид:
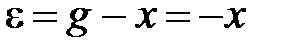 ,
,
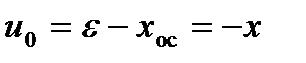 ,
, 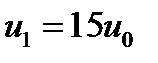 , (1)
, (1)
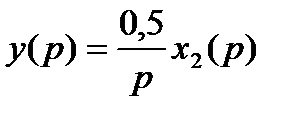 ,
, 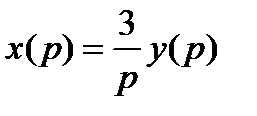 или
или 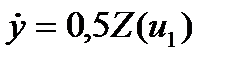 ,
, 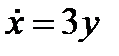 (2)
(2)
Нелинейный элемент имеет симметрическую нечетную характеристику (1). Её аналитическое описание:
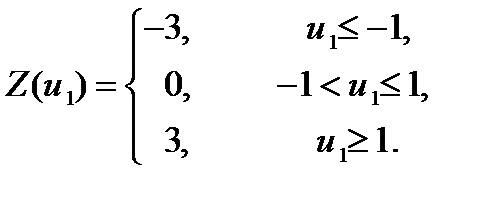 (3)
(3)
Исключим промежуточные переменные и представим уравнения системы (1) – (3). В результате получим
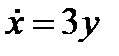 ,
, 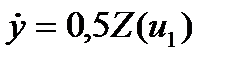 , (4)
, (4)
где
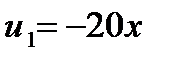 . (5)
. (5)
Как видно, рассматриваемая динамическая система (схема 1.) описывается двумя переменными состояния, т.е. имеет второй порядок и может быть исследована методом фазовой плоскости.
Как известно, дифференциальное уравнение фазовых траекторий получается из системы (5) путем деления второго уравнения на первое. В результате получается соотношение
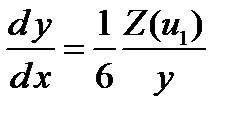 ,
,
из которого следует дифференциальное уравнение
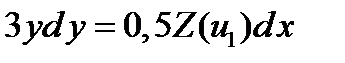 . (6)
. (6)
Это уравнение можно проинтегрировать лишь для отдельных областей фазовой плоскости. В рассматриваемом случае эти области образуются линиями переключения, т.е. линиями, которые соответствуют тем значениям переменных состояния 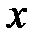 и
и 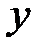 , при которых происходит изменение значения нелинейности. В рассматриваемом случае это значения
, при которых происходит изменение значения нелинейности. В рассматриваемом случае это значения 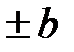 переменной
переменной 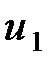 , при которых переключается реле. При
, при которых переключается реле. При 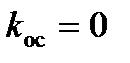 эта переменная, как видно из равенства (5), зависит от переменной состояния
эта переменная, как видно из равенства (5), зависит от переменной состояния 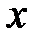 .
.
Они определяются вытекающими из (5) при 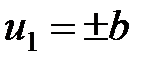 выражениями
выражениями
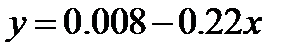 ,
, 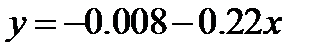
Проинтегрировав уравнение (6) для трех областей I, II, III фазовой плоскости, где 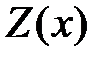 равна
равна 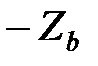 , нулю или
, нулю или 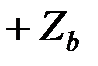 получим алгебраические уравнения фазовых траекторий для каждой из этих областей:
получим алгебраические уравнения фазовых траекторий для каждой из этих областей:
I 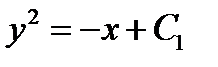 , при
, при 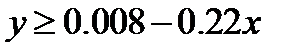 ; (7)
; (7)
II 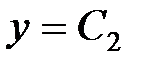 , при
, при 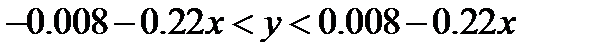 ; (8)
; (8)
III 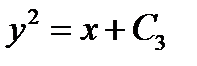 , при
, при 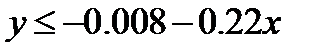 , (9)
, (9)
где 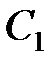 ,
, 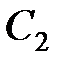 ,
, 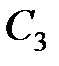 – постоянные интегрирования.
– постоянные интегрирования.
Сначала построим фазовые траектории системы при двух значениях гибкого коэффициента обратной связи 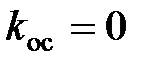 ,
, 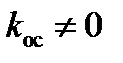 .
.
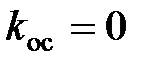 :
:
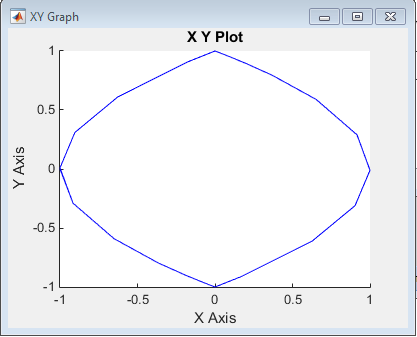
Рис.1 Фазовая траектория при коэффициенте гибкой обратной связи 0
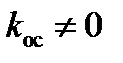
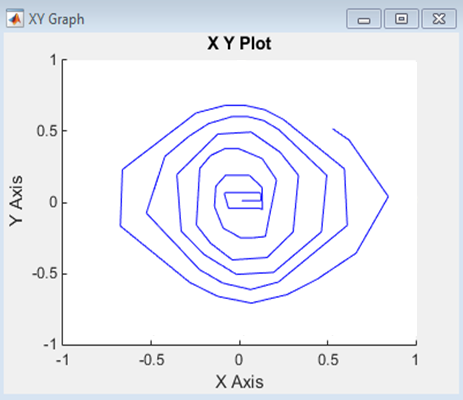
Рис.2 Фазовая траектория при коэффициенте гибкой обратной связи отличным от нуля
Зная, что фазовый портрет – это полная совокупность различных фазовых траекторий , построим фазовый портрет системы. Меняя каждый раз коэффициент гибкой обратной связи получим:
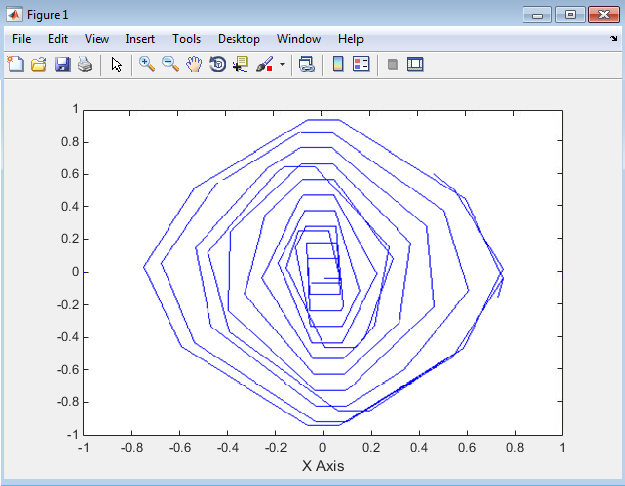
Рис. 3 Фазовый портрет системы
Он даёт представление о совокупности всех возможных состояний системы и типах возможных движений в ней.
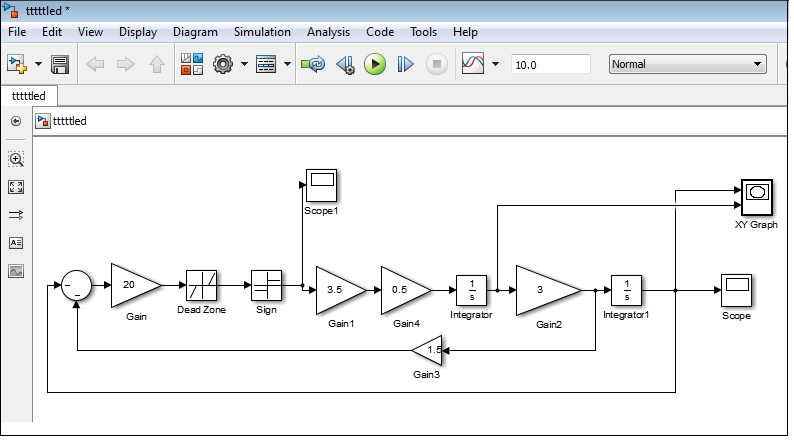
Рис. 4 Структурная схема набранная в Simulink
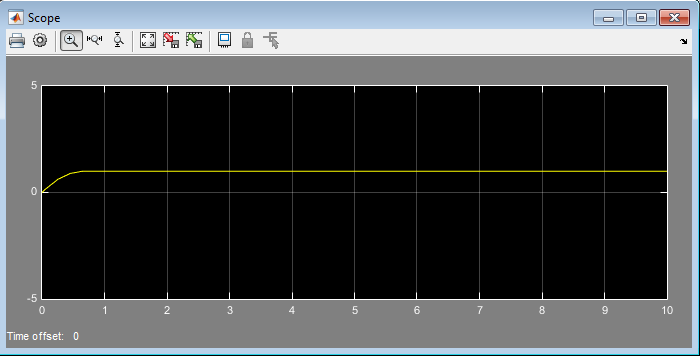
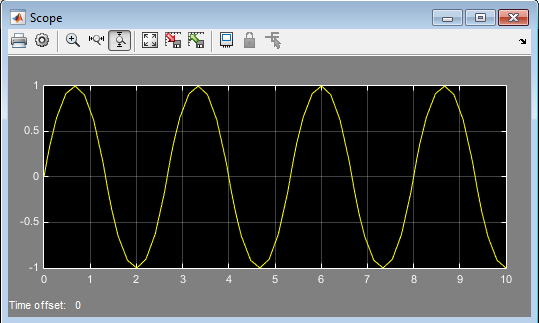
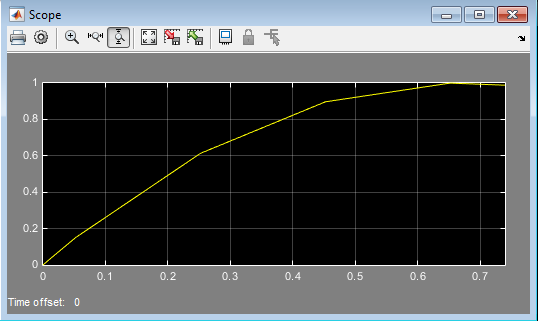
Рис. 4 Кривая переходного процесса, 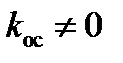
Вывод: Мы изучили метод фазовой плоскости. Исследовали влияние гибкой обратной связи на переходные процессы нелинейных систем управления второго порядка. Так же мы выяснили, что по известной фазовой траектории можно построить приближенную кривую переходного процесса и установили, что увеличение коэффициента обратной связи приводит к уменьшению по модулю угла наклона линий переключения и, как следствие, к уменьшению числа колебаний за время переходного процесса. Что показывает следующий переходный процесс при 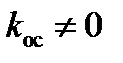
А при отсутствии обратной связи, фазовые траектории превращаются в циклы, а движение системы становится незатухающим.
Что мы и видим на графике переходного процесса при 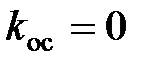 :
: