Пример 7.27. Найти корреляционную функцию стационарного случайного процесса X(t), если её спектральная плотность постоянна на интервале и равна с, а вне этого интервала равна нулю.
Решение. Имеем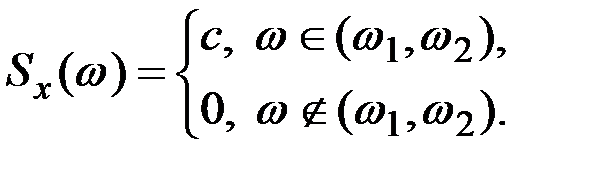 
По определению корреляционной функции
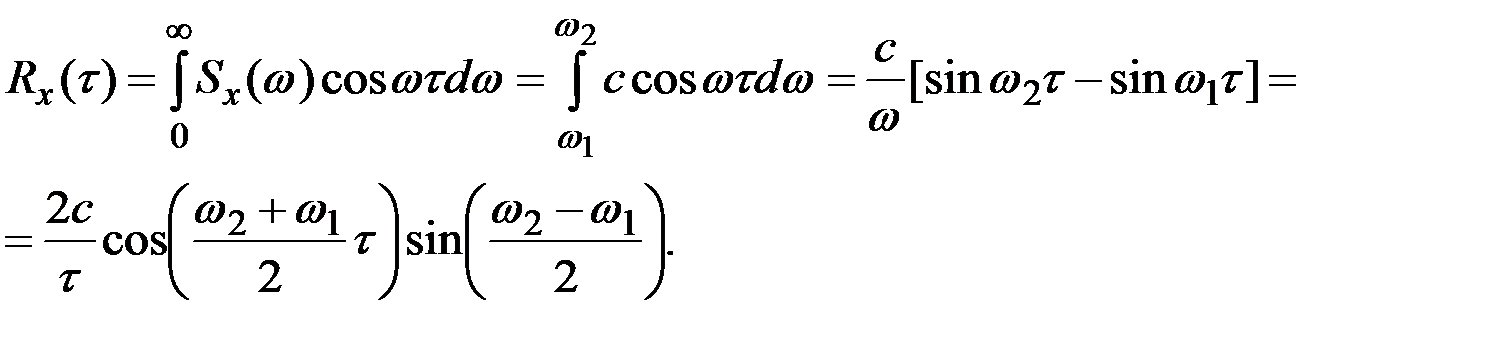
Дисперсия рассматриваемого случайного процесса X(t) будет
.
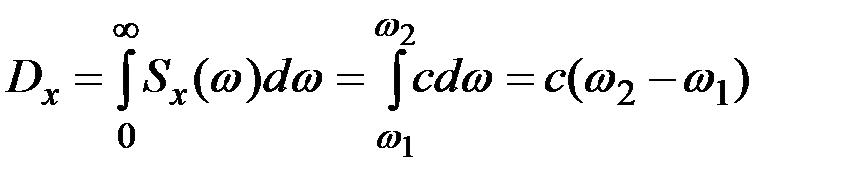Отсюда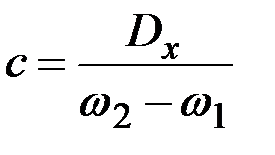 
.
Следовательно
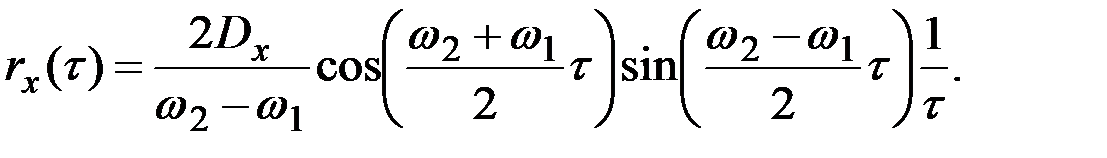
Рассмотрим предел этого выражения при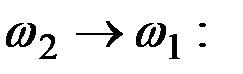 
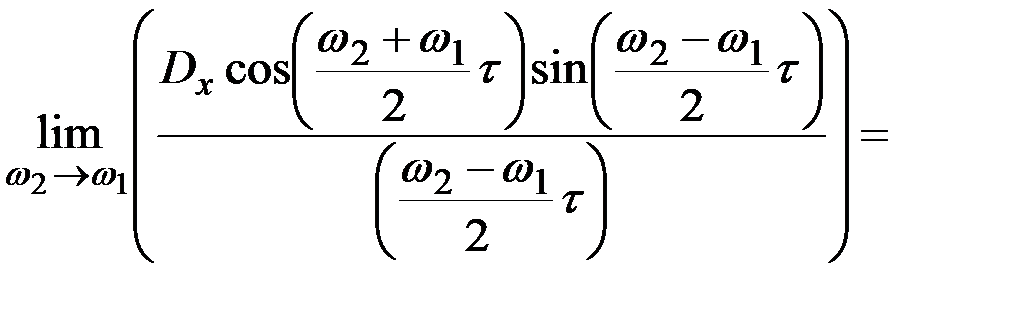
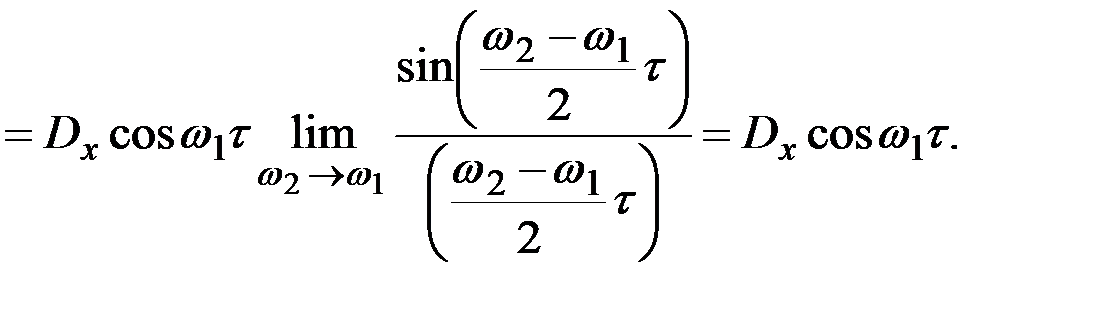
Таким образом, при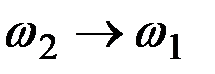 
мы получили случай, когда X(t) является элементарным стационарным случайным процессом – случайные колебания на частоте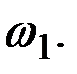 
Пример 7.28. Найти спектральную плотность процесса X(t), представляющего собой случайную телеграфную волну с корреляционной функцией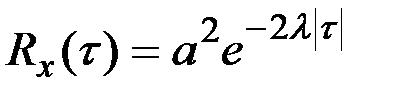 
.
Решение. Спектральную плотность процесса X(t) вычислим так:
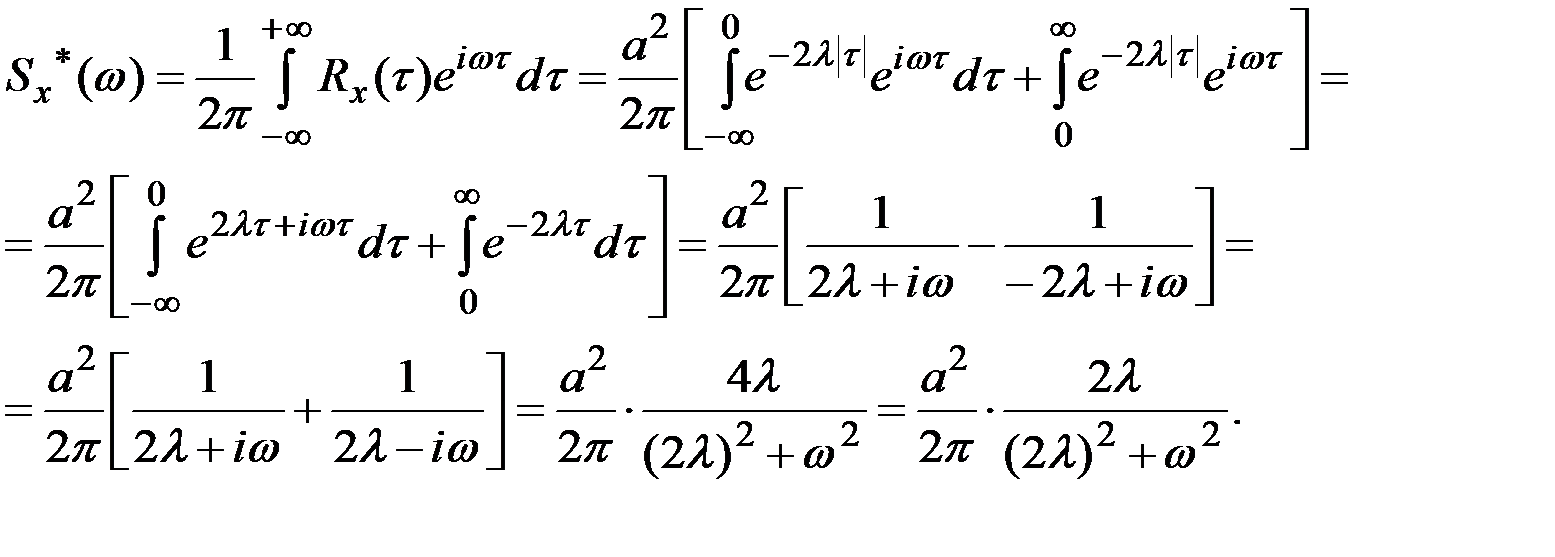
Пример 7.29. Показать, что не существует никакой стационарной СФ X(t), корреляционная функция которой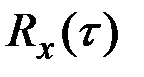 
постоянна в каком–то интервале (– t, t) и равна нулю вне его.
Решение. Предположим противное, т.е. что существует случайная функция X(t), для которой АКФ равна значению b ¹ 0 при |t| < t1 и равна 0 при |t| > t1. Найдём спектральную плотность СФ X(t):
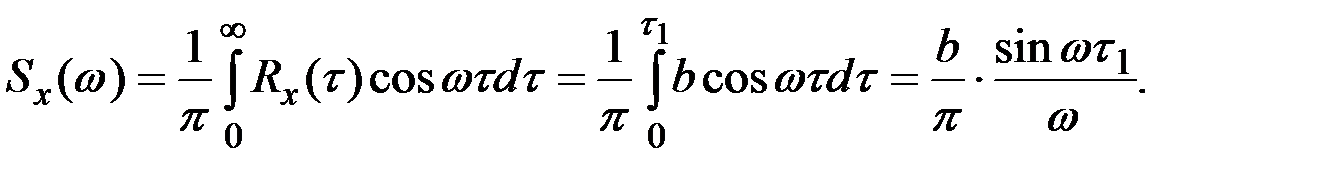
Видно, что функция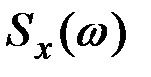 
для некоторых значений w отрицательна, что противоречит свойствам спектральной плотности. Следовательно, корреляционная функция указанного выше вида существовать не может.
Пример 7.30. Какова размерность: 1) функции распределения случайного процесса; 2) плотности распределения; 3) математического ожидания; 4) дисперсии; 5) среднеквадратического отклонения; 6) корреляционной функции; 7) спектральной плотности; 8) нормированной корреляционной функции; 9) нормированной спектральной плотности; 10) взаимной корреляционной функции?
Решение. 1) безразмерная; 2) обратная размерность случайного процесса; 3) размерность случайного процесса; 4) размерность квадрата случайного процесса; 5) размерность случайного процесса; 6) размерность квадрата случайного процесса; 7) размерность квадрата случайного процесса, делённая на размерность частоты; 8) безразмерная; 9) обратная размерность частоты; 10) размерность одного процесса, умноженная на размерность другого.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ № 7
Задание. Мощность угольного пласта с математическим ожиданием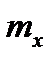 
метров является нормальной стационарной СФ по направлению отработки с автокорреляционной функцией 
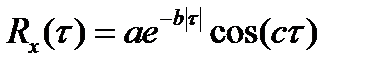(τ – в метрах). Скорость продвижения забоя равна V м/ч. В текущий момент обработки пласта его мощность равна 
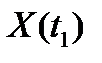м. Определить вероятность того, что через 2 часа работы ( 
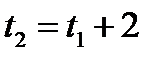) мощность пласта будет больше 
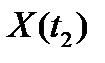м.
Исходные данные по вариантам представлены ниже в табл. 7.4.
Таблица 7.4
Исходные данные для исследования
| № п/п |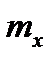
|
|
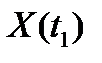
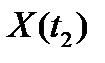
| V | a | b | c |
| 1 | 4,0 | 3,8 | 3,9 | 1,4 | 1,5 | 0,14 | 0,25 |
| 2 | 3,6 | 3,5 | 3,8 | 1,5 | 1,2 | 0,23 | 0,31 |
| 3 | 3,8 | 3,7 | 4,0 | 1,6 | 1,3 | 0,15 | 0,22 |
| 4 | 3,0 | 3,3 | 3,4 | 1,7 | 1,4 | 0,12 | 0,25 |
| 5 | 3,2 | 3,5 | 3,9 | 1,3 | 1,6 | 0,16 | 0,41 |
| 6 | 3,9 | 3,2 | 3,5 | 1,2 | 1,1 | 0,13 | 0,12 |
| 7 | 3,2 | 3,8 | 3,9 | 1,4 | 1,5 | 0,13 | 0,21 |
| 8 | 3,6 | 3,6 | 3,8 | 1,5 | 1,2 | 0,22 | 0,31 |
| 9 | 3,8 | 3,9 | 4,2 | 1,6 | 1,3 | 0,15 | 0,22 |
| 10 | 3,0 | 3,3 | 3,8 | 1,7 | 1,4 | 0,12 | 0,25 |
| 11 | 3,2 | 3,5 | 3,9 | 1,3 | 1,6 | 0,16 | 0,19 |
| 12 | 3,9 | 3,8 | 4,3 | 1,2 | 1,1 | 0,13 | 0,12 |
| 13 | 4,2 | 4,4 | 4,9 | 1,4 | 1,5 | 0,21 | 0,21 |
| 14 | 4,6 | 4,6 | 4,9 | 1,5 | 1,2 | 0,18 | 0,31 |
| 15 | 4,8 | 4,7 | 5,0 | 1,6 | 1,3 | 0,15 | 0,22 |
| 16 | 4,0 | 4,3 | 4,7 | 1,7 | 1,4 | 0,12 | 0,25 |
| 17 | 5,2 | 5,5 | 4,9 | 1,3 | 1,6 | 0,16 | 0,28 |
| 18 | 4,9 | 4,2 | 4,5 | 1,2 | 1,1 | 0,13 | 0,12 |
| 19 | 4,2 | 4,3 | 3,9 | 1,4 | 1,5 | 0,16 | 0,23 |
| 20 | 3,6 | 3,9 | 3,4 | 1,5 | 1,2 | 0,27 | 0,33 |
| 21 | 3,8 | 3,7 | 4,0 | 1,6 | 1,3 | 0,15 | 0,22 |
| 22 | 3,0 | 3,3 | 3,5 | 1,7 | 1,4 | 0,12 | 0,25 |
| 23 | 3,2 | 3,5 | 3,0 | 1,3 | 1,6 | 0,16 | 0,38 |
| 24 | 3,9 | 3,2 | 3,5 | 1,2 | 1,1 | 0,13 | 0,12 |
| 25 | 4,2 | 3,7 | 4,0 | 1,6 | 1,3 | 0,15 | 0,22 |
| 26 | 4,0 | 3,3 | 3,9 | 1,7 | 1,4 | 0,12 | 0,25 |
| 27 | 5,2 | 5,5 | 4,9 | 1,3 | 1,6 | 0,16 | 0,36 |
| 28 | 4,9 | 4,2 | 4,5 | 1,2 | 1,1 | 0,13 | 0,12 |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Основы моделирования и первичная обработка данных. – М.: Финансы и статистика, – 1983. – 471 с.
2. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М.: ЮНИТИ, 1998. – 1022 с.
3. Аренс Х., Лёйтер Ю. Многомерный дисперсионный анализ / пер. с нем. – М.: Финансы и статистика, 1985. – 230 с.
4. Бендат Дж., Пирсол А. Измерение и анализ случайных процессов. – М.: Мир, 1974. – 464 с.
5. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 540 с.