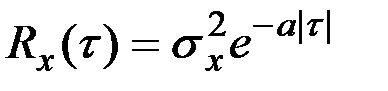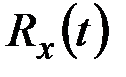Средняя площадь , ограниченная реализацией нормальной стационарной случайной функции выше заданного уровня a во время выброса, определяется зависимостью
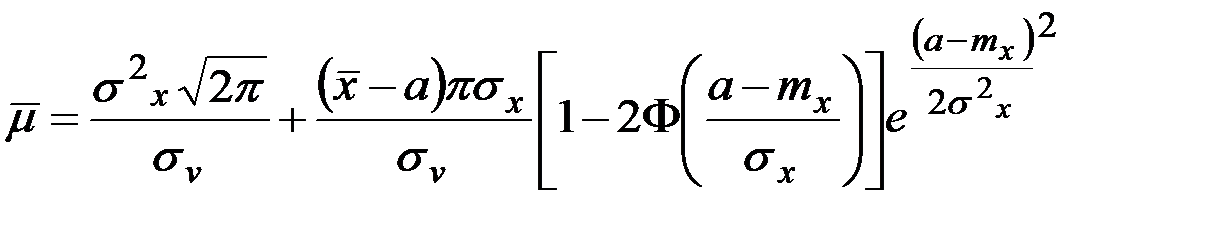 .
.
Пример 7.9. Напряжение на выходе устройства является нормальным случайным процессом с нулевым математическим ожиданием и корреляционной функцией
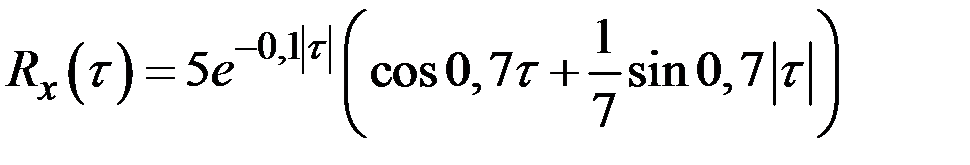 (
( 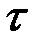 – в секундах).
– в секундах).
Определить, сколько раз в среднем в течение времени T = 8 мин. напряжение на выходе устройства будет равно нулю.
Решение. Среднее число выбросов за нулевой уровень
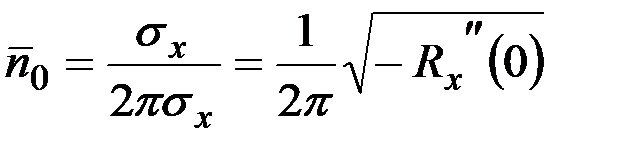 .
.
Так как
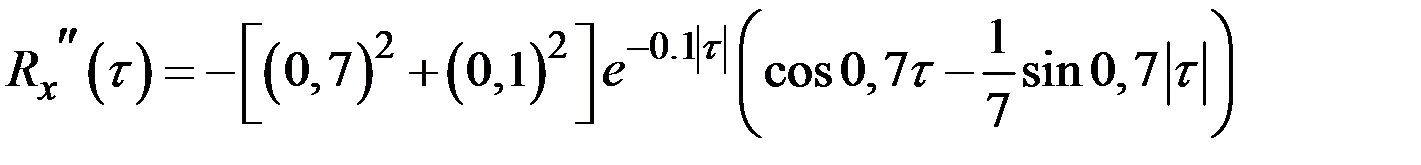 ,
,
то
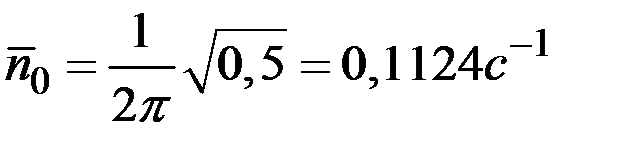 ,
,
а число выбросов за 8 мин.
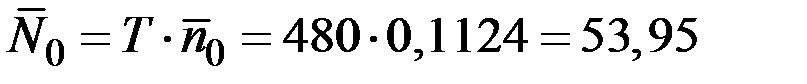 .
.
Так как нулевое значение напряжения принимает дважды при осуществлении выброса (пересечение процессом нулевого уровня как при увеличении, так и при уменьшении напряжения), то напряжение на выходе устройства будет равно нулю примерно 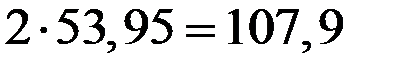 » 108 раз.
» 108 раз.
Пример 7.10. Генератор тока рассчитан на постоянную мощность a, потребляемую в сети. Действительное потребление тока характеризуется мощностью W(t), которая является нормальной СФ времени. В том случае, когда потребляемая мощность превосходит расчётную, включается резервный генератор, мощность которого практически не ограничена. Определить среднюю энергию, затрачиваемую резервным генератором в течение одного выброса функции W(t) за уровень a, если математическое ожидание 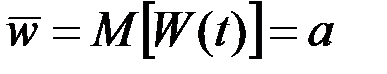 , а корреляционная функция
, а корреляционная функция
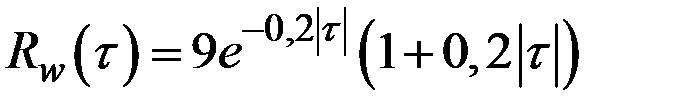 .
.
Решение. Искомая энергия представляет собой площадь выброса, поэтому 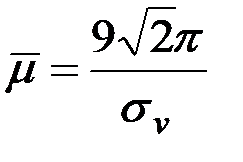 .
.
Величину 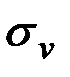 определяем из выражения
определяем из выражения
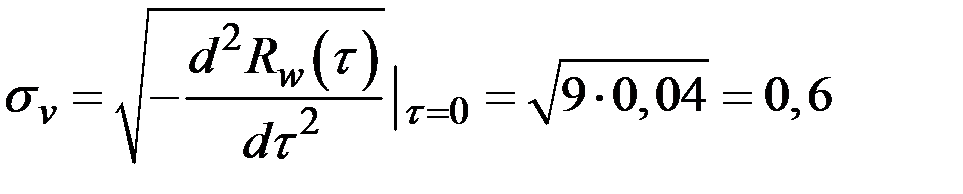 .
.
Следовательно, 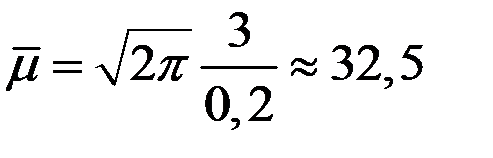 .
.
Пример 7.11. Содержание железа в рудном блоке длиной 800 метров по направлению его отработки является нормальной случайной функцией со средним значением 17% и корреляционной функцией
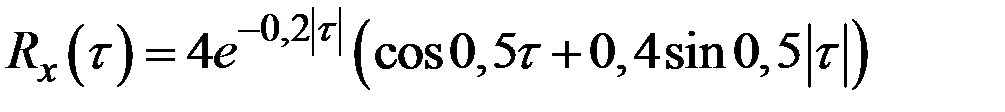 (
( 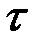 – в метрах).
– в метрах).
Определить, сколько раз в среднем за время отработки блока содержание железа будет выходить за пределы 17 ± 3%.
Решение. Искомое число выбросов 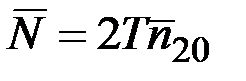 .
.
Коэффициент 2 появляется вследствие того, что надо учитывать как выбросы снизу вверх за уровень a = 20%, так и выбросы сверху вниз за уровень 14%. T – длина блока.
Подставляя данные задачи в соответствующую формулу, получим соотношение
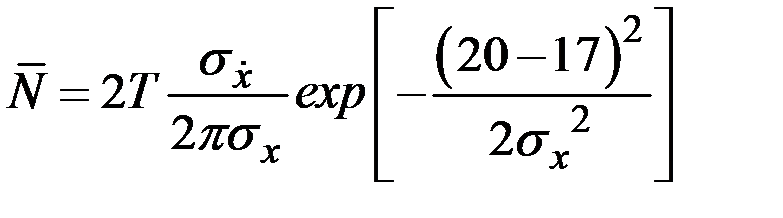 .
.
Определим 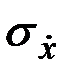
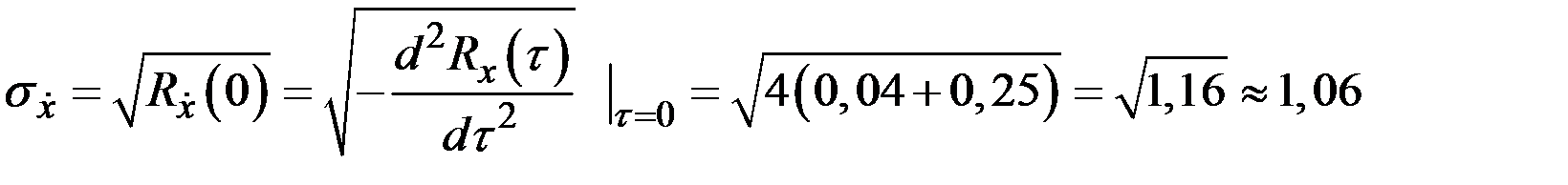 .
.
Тогда
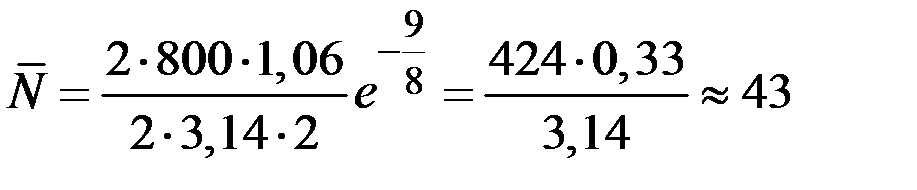 раза.
раза.
Пример 7.12. Для условий предыдущего примера определим вероятности 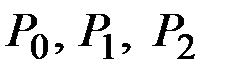 того, что на первых 20,5 метрах не будет ни одного выхода содержания железа за пределы 17 ± 3%; будет один выход; два выхода.
того, что на первых 20,5 метрах не будет ни одного выхода содержания железа за пределы 17 ± 3%; будет один выход; два выхода.
Решение. Считая допустимым приближенно пользоваться законом Пуассона, получаем:
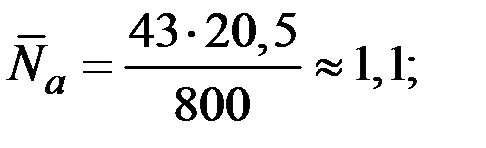
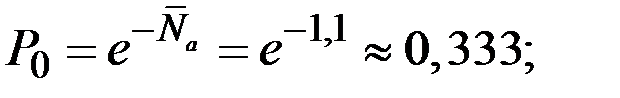
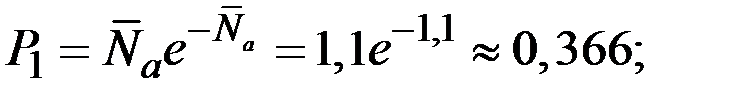
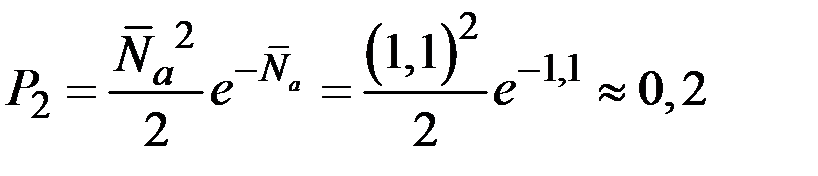 .
.
Некоторой проверкой допустимости применения закона Пуассона в данном случае может служить тот факт, что для среднего расстояния между выбросами 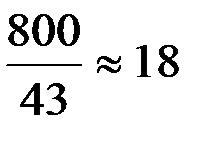 метров нормированная корреляционная функция при
метров нормированная корреляционная функция при 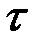 = 18 равна нулю:
= 18 равна нулю:
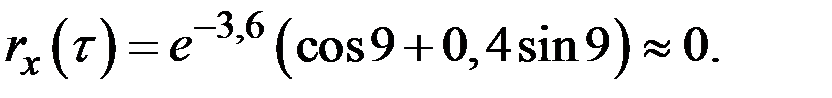
Пример 7.13. На вход цепи аппаратов обогатительной фабрики непрерывно подаётся руда со средним содержанием железа 23%. Содержание железа в руде является нормальной случайной функцией времени с АКФ 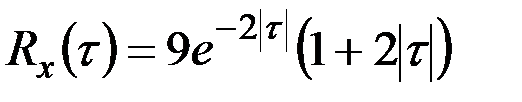 (
( 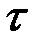 – в часах). Руда считается кондиционной, если содержание железа в ней не ниже 21%. Определить среднюю продолжительность поступления некондиционной руды.
– в часах). Руда считается кондиционной, если содержание железа в ней не ниже 21%. Определить среднюю продолжительность поступления некондиционной руды.
Решение. Средняя длительность выброса нормального случайного процесса X(t) за уровень a определяется формулой
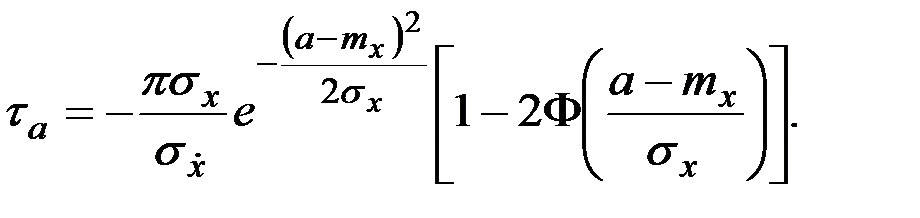
В данном случае
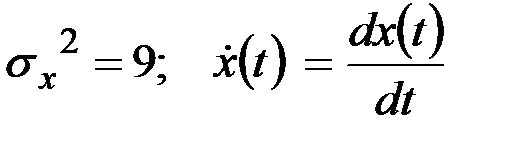 ;
;
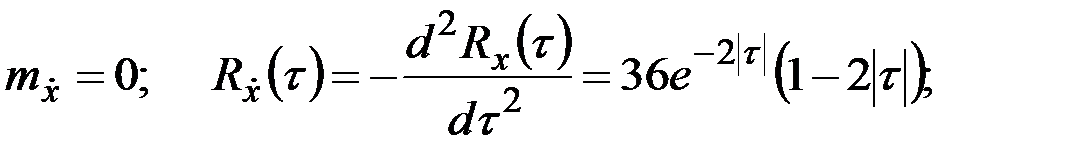
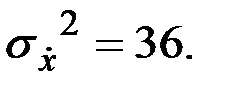
Тогда
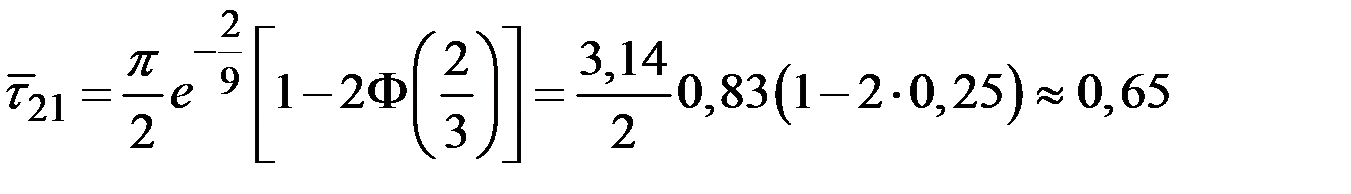 ч » 40 мин.
ч » 40 мин.
Средняя продолжительность поступления некондиционной руды составляет около 40 мин.
Пример 7.14. Определить среднее число точек перегиба нормальной стационарной случайной функции X(t), приходящееся на время T, если
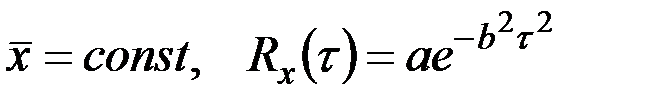 .
.
Решение. Искомое число равно числу выбросов в обе стороны за нулевой уровень.
Следовательно,
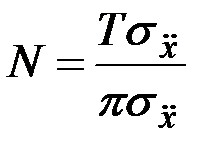 .
.
Определив корреляционные функции процессов и вычислив средние квадратические отклонения 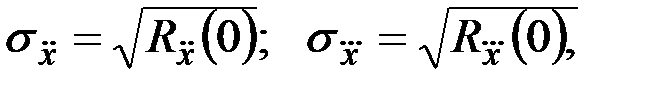 окончательно будем иметь:
окончательно будем иметь:
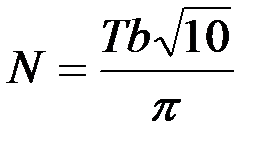 .
. 
Пример 7.15. Траектория полёта летательного аппарата в вертикальной плоскости описывается уравнениями
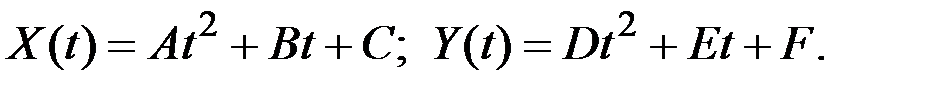
Коэффициенты A, B, C, D, E, F являются случайными величины с математическими ожиданиями a, b, c, d, e, f соответственно и с дисперсиями 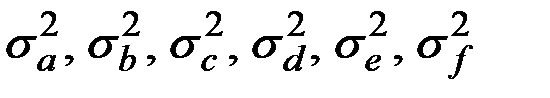 . Нормированная корреляционная матрица коэффициентов имеет вид:
. Нормированная корреляционная матрица коэффициентов имеет вид:

Определить математическое ожидание, АКФ и дисперсию горизонтальной и вертикальной составляющих скорости аппарата.
Решение. Из условий задачи следует, что составляющие скорости выражаются зависимостями:
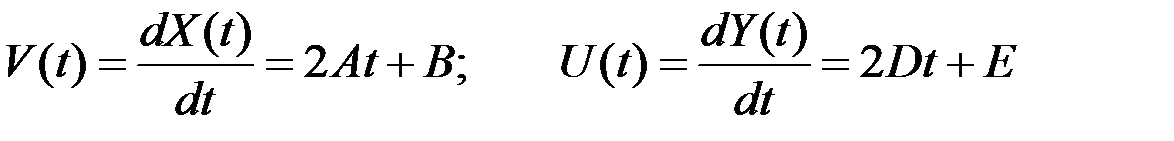 .
.
Если
Y(t) = r(t)X(t) + j(t),
то mY(t) = r(t)mX(t) + j(t),
RY(t1, t2) = r *(t1)r(t2)R(t1, t2).
Используя эти формулы, имеем:
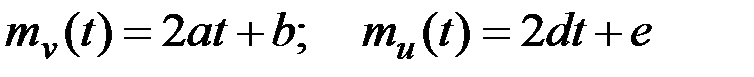 .
.
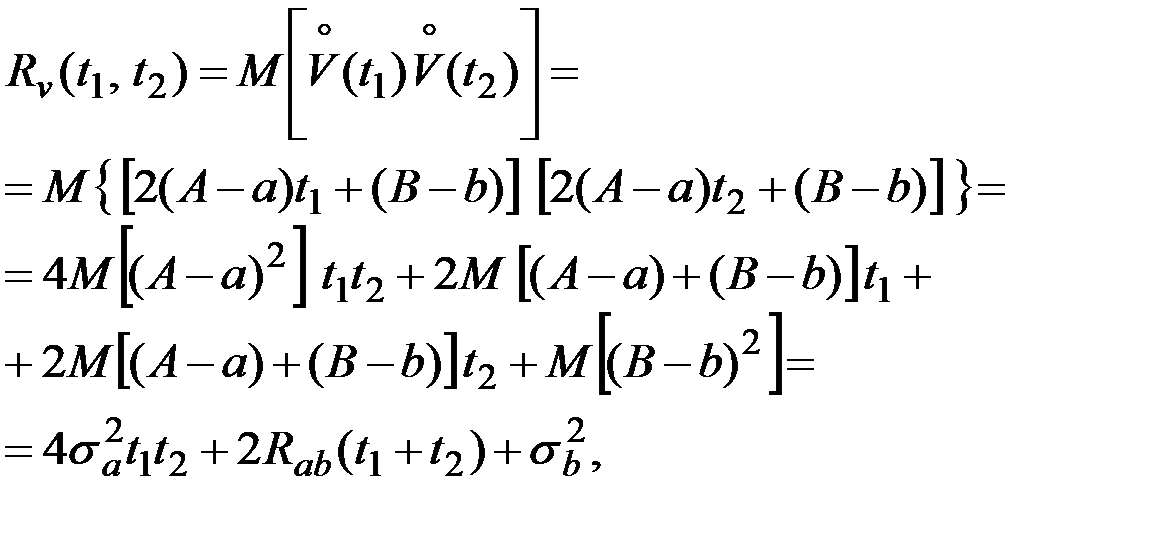
где 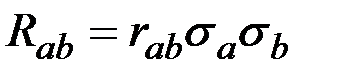 .
.
Подставляя исходные данные, имеем:
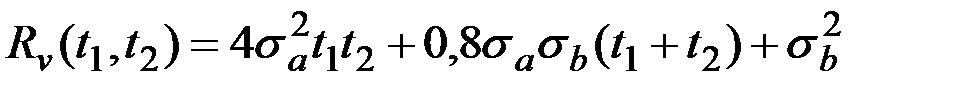 .
.
Аналогично получаем АКФ второй составляющей скорости:
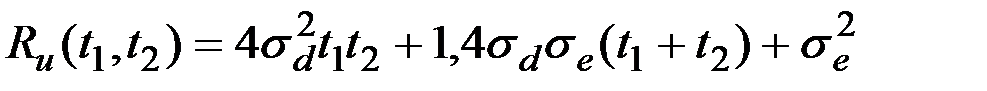 .
.
При 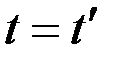 получаем дисперсии составляющих скорости:
получаем дисперсии составляющих скорости:
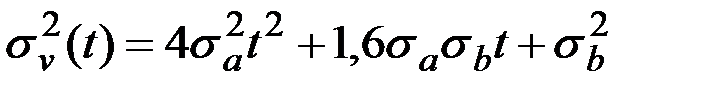 ,
,
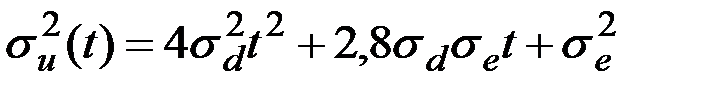 .
.
Пример 7.16. Случайная функция имеет характеристики:
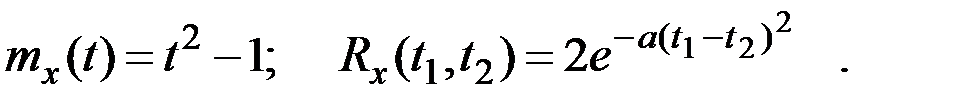
Определить характеристики случайных функций
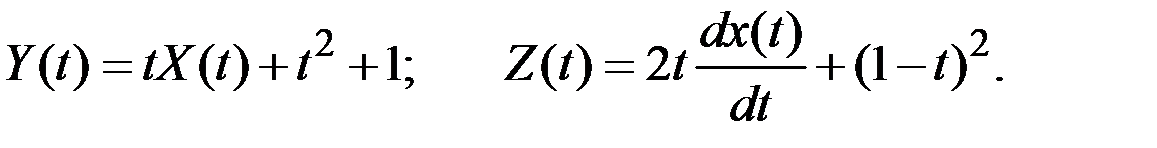
Решение. Искомые характеристики вычислим по их определению.
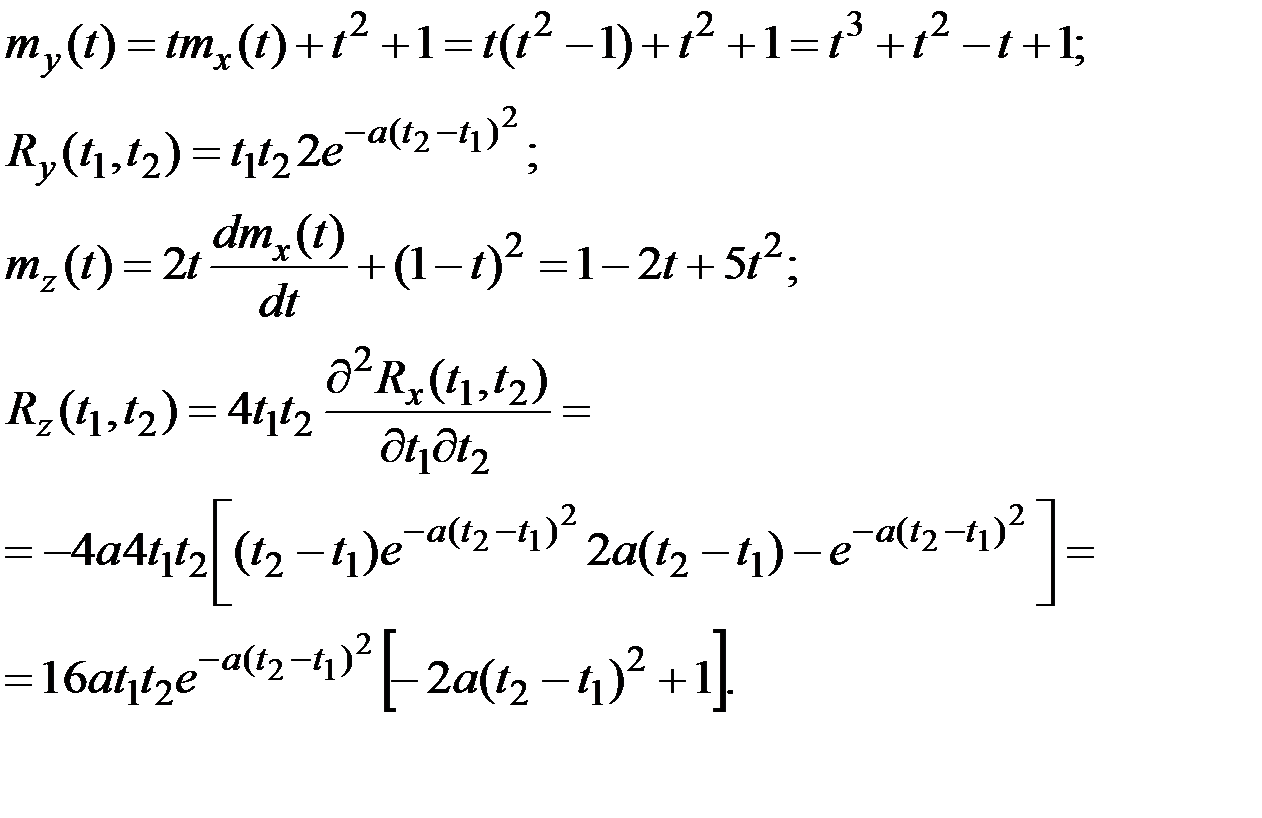
Пример 7.17. Случайная функция X(t) имеет характеристики
mx(t) = 1; 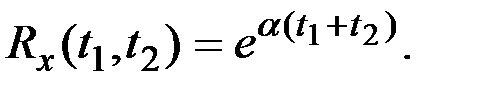
Определить характеристики случайной функции 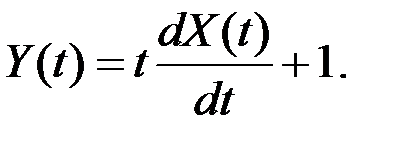
Определить, являются ли стационарными СФ X(t) и Y(t).
Решение. В силу линейности преобразования 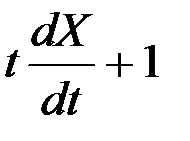 получаем характеристики СФ Y(t):
получаем характеристики СФ Y(t):
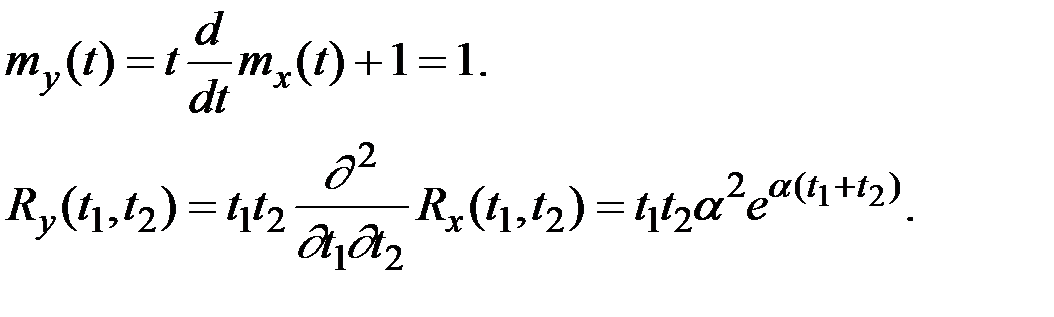
Ни одна из случайных функций X(t) и Y(t) не является стационарной, так как их корреляционные функции зависят не только от t = t2 – t1, но от каждого из аргументов t1, t2 .
Пример 7.18. Случайная функция X(t) имеет характеристики:
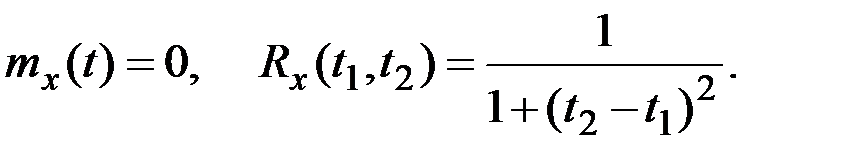
Найти характеристики СФ 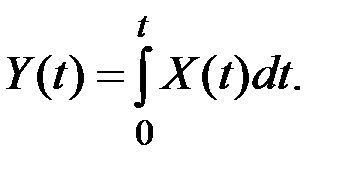
Определить, стационарны ли случайные функции X(t) и Y(t).
Решение. В силу линейности преобразования 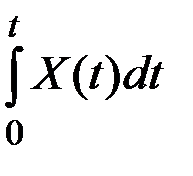 получаем характеристики случайной функции Y(t):
получаем характеристики случайной функции Y(t):
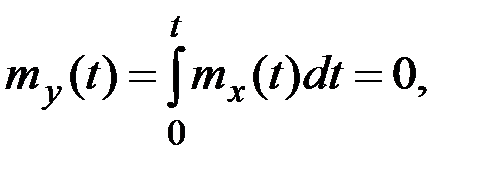
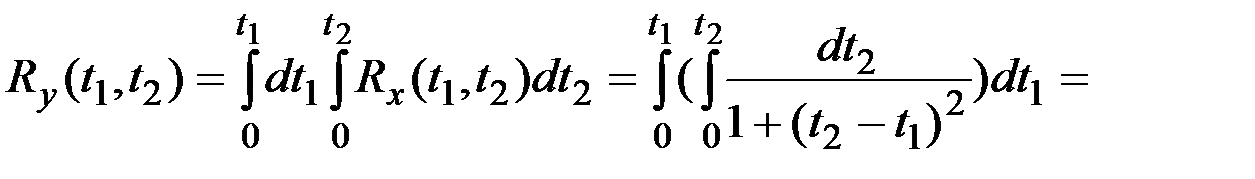
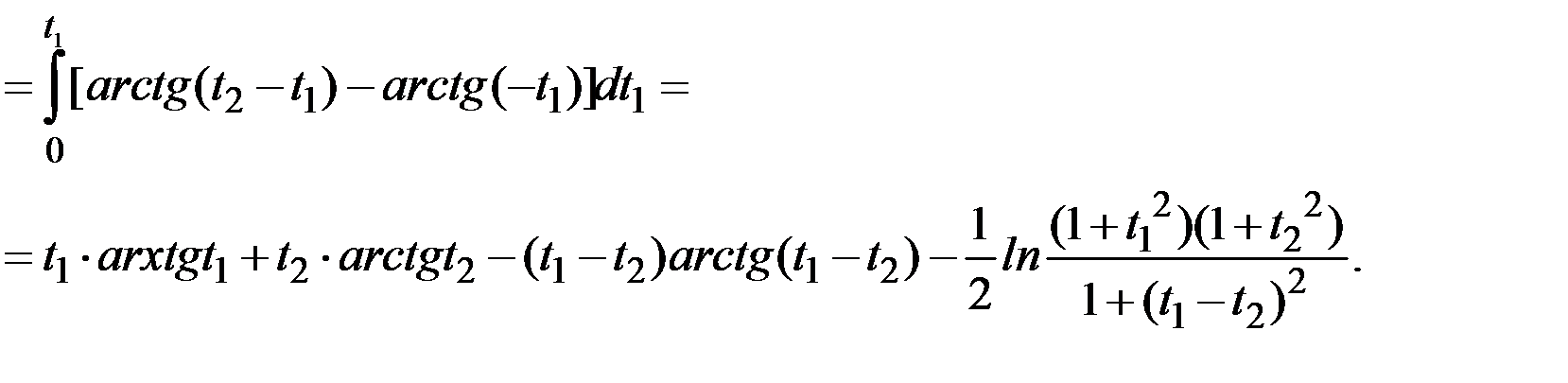
Случайная функция X(t) стационарна: 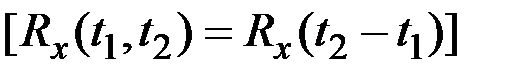 .
.
Случайная функция 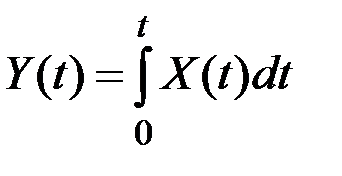 не стационарна.
не стационарна.
Действительно, дисперсия этой случайной функции равна
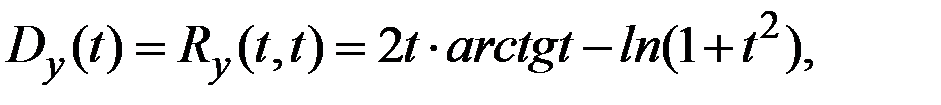
то есть зависит от t .
Пример 7.19. СФ X(t) задана выражением 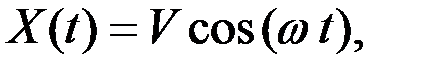 где V – СВ с характеристиками
где V – СВ с характеристиками 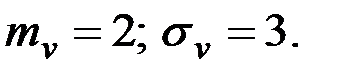 Найти характеристики случайной функции X(t):
Найти характеристики случайной функции X(t): 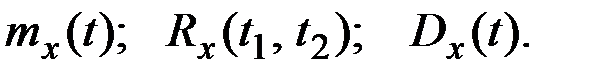 Найти характеристики СФ
Найти характеристики СФ 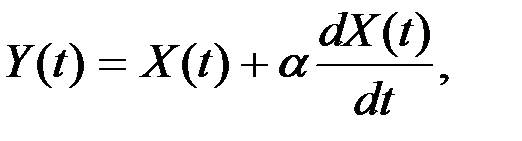 где a – неслучайная величина. Является ли стационарными СФ X(t) и Y(t)?
где a – неслучайная величина. Является ли стационарными СФ X(t) и Y(t)?
Решение. После несложных вычислений получим:
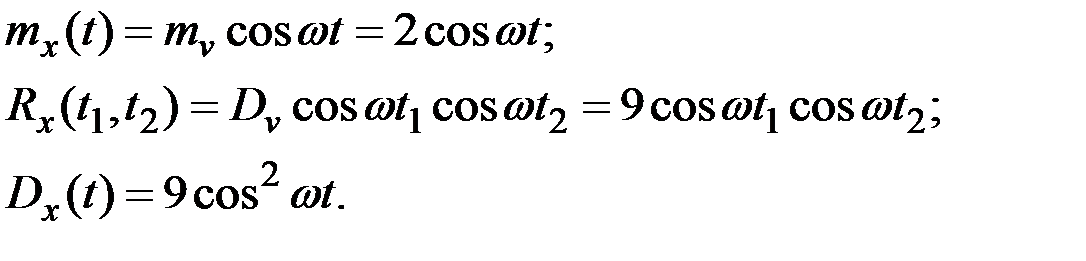
Случайную функцию Y(t) можно представить в виде
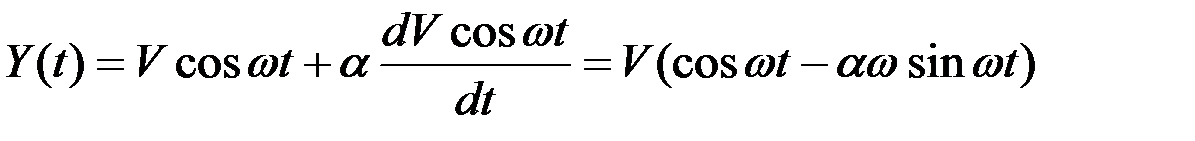 .
.
Отсюда получаем
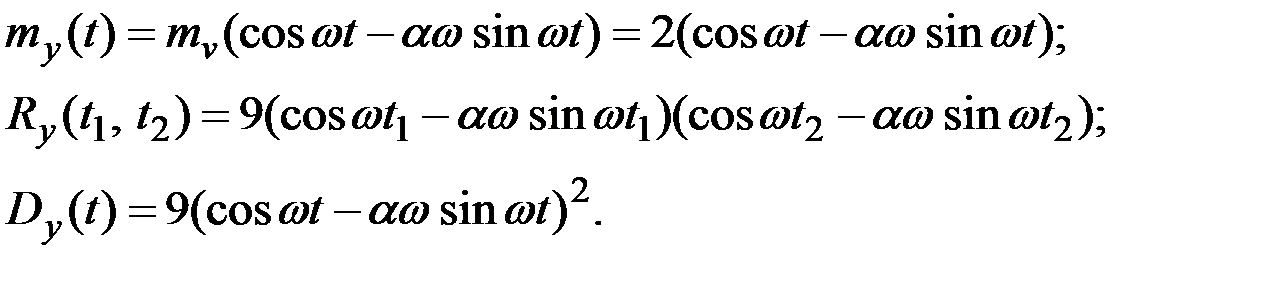
Случайные функции X(t) и Y(t) не стационарны.
Пример 7.20. Случайнаяе функция X(t) с характеристиками 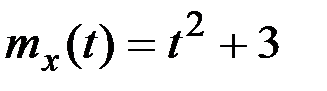 и
и 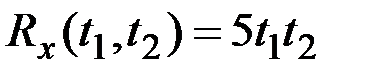 подвергается преобразованию
подвергается преобразованию
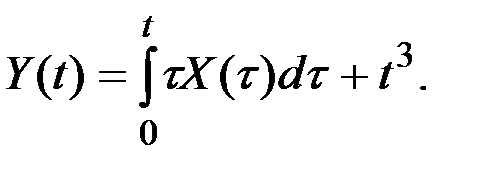
Определить характеристики СФ Y(t): 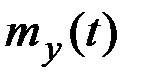 и
и 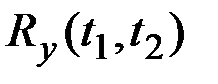 .
.
Решение.
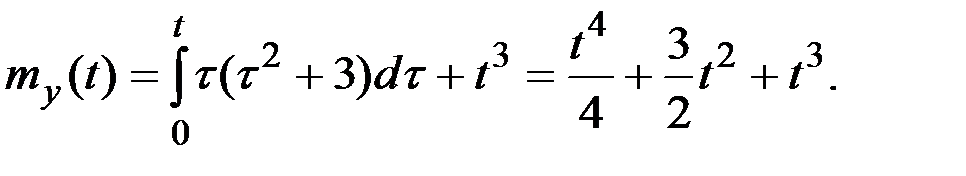
Однородная часть преобразования 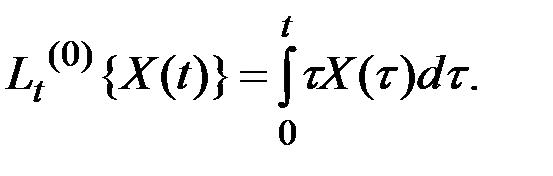
Тогда
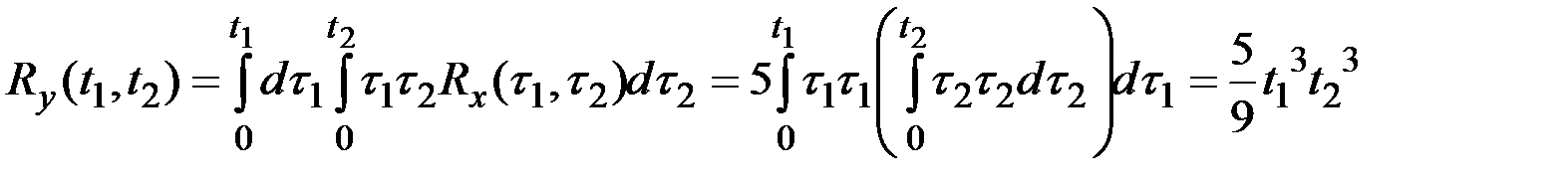 .
.
7.6. Спектральное представление стационарных процессов
Стационарные случайные процессы, вследствие неизменности их вероятностных характеристик во времени, имеют квазипериодический характер. Это позволяет заменить исследование стационарной функции времени исследованием СФ некоторой вспомогательной переменной, которая во многих технических приложениях имеет размерность частоты.
Полученные таким способом результаты оказываются полностью эквивалентными результатам, получаемым с помощью корреляционной функции случайного процесса. Однако применение этого способа во многих случаях позволяет значительно упростить выкладки и добиться большей наглядности. Поэтому данный способ получил широкое применение, как в теоретических исследованиях, так и в различных технических и экономических приложениях.
Случайная функция 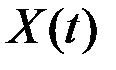 может быть представлена в виде суммы гармонических колебаний с различными частотами (не обязательно кратными) и случайными амплитудами. Реализацию процесса на конечном интервале
может быть представлена в виде суммы гармонических колебаний с различными частотами (не обязательно кратными) и случайными амплитудами. Реализацию процесса на конечном интервале 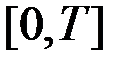 можно представить в виде ряда Фурье
можно представить в виде ряда Фурье
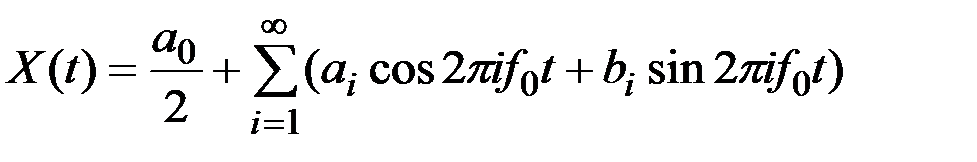 ,
,
где 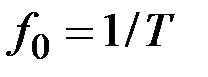 ;
;
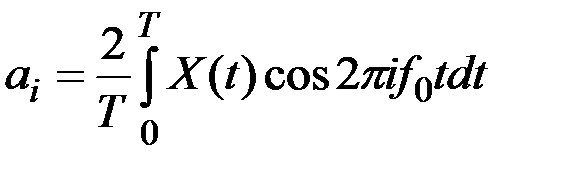 ,
, 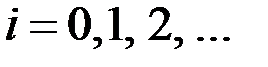 ;
;
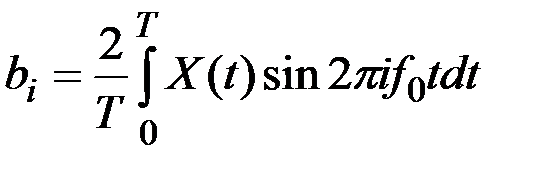 ,
, 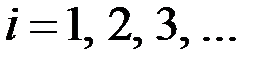
Если реализация процесса задана в виде дискретной последовательности и состоит из чётного числа 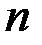 наблюдений с интервалом дискретности
наблюдений с интервалом дискретности 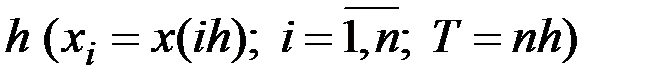 , то ряд Фурье по всем
, то ряд Фурье по всем 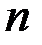 значениям имеет вид
значениям имеет вид
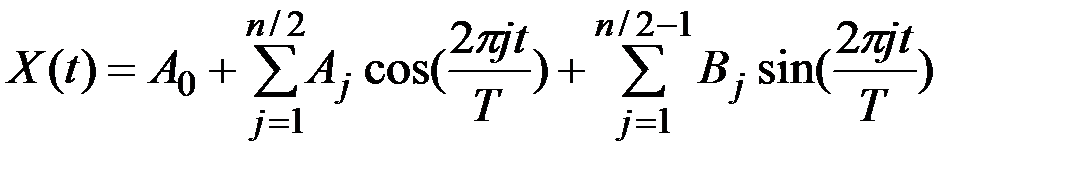 .
.
Коэффициенты этого ряда определяются выражениями:
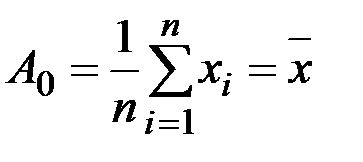 ;
;
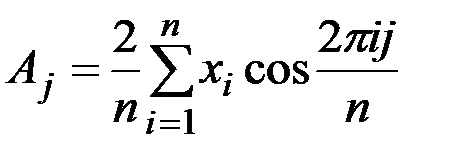 ;
; 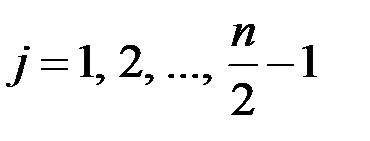 ;
;
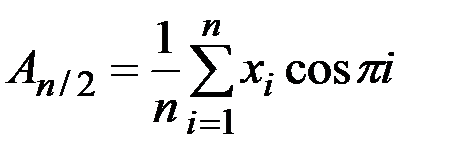 ;
;
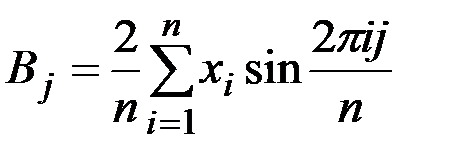 ;
; 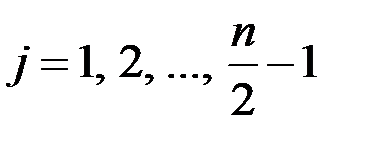 .
.
В математике, физике, технике широко применяется понятие "спектр". Если какой–либо колебательный процесс представляется в виде суммы гармонических колебаний различных частот ("гармоник"), то спектром колебательного процесса называется функция, описывающая распределение амплитуд по различным частотам.
Спектр показывает, какого рода колебания преобладают в данном процессе, какова его внутренняя структура.
Аналогичное спектральное описание можно дать и стационарному случайному процессу. Для случайного процесса амплитуды колебаний будут случайными величинами. Спектр стационарной СФ будет описывать распределение дисперсий по различным частотам, т.е. частотный состав процесса.
Рассмотрим стационарную СФ 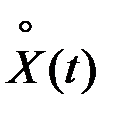 , которую мы наблюдаем на интервале
, которую мы наблюдаем на интервале 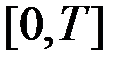 . Корреляционная функция процесса есть чётная функция и на графике изобразится симметричной кривой (рис.7.10).
. Корреляционная функция процесса есть чётная функция и на графике изобразится симметричной кривой (рис.7.10).
При изменении параметров 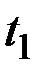 и
и 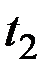 от 0 до T аргумент
от 0 до T аргумент 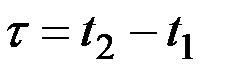 изменяется от –T до T.
изменяется от –T до T.
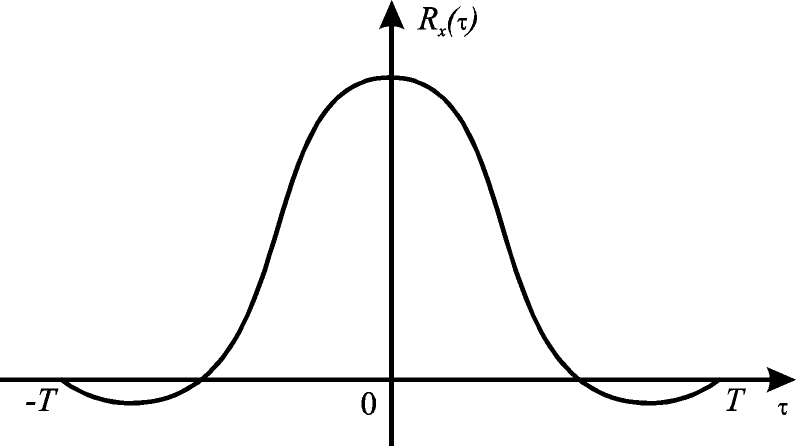
Рис.7.10. Типичный график корреляционной функции
Известно, что чётную функцию на интервале 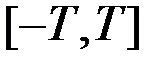 можно разложить в ряд Фурье, пользуясь только чётными (косинусными) гармониками
можно разложить в ряд Фурье, пользуясь только чётными (косинусными) гармониками
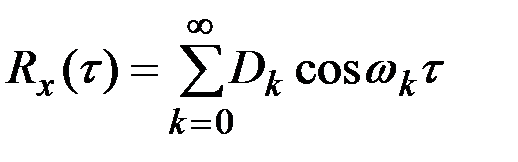 ,
,
где 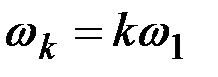 ;
; 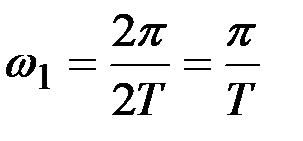 ,
,
а коэффициенты 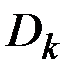 определяются формулами
определяются формулами
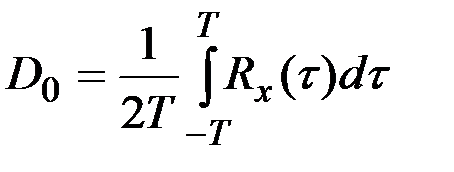 ;
; 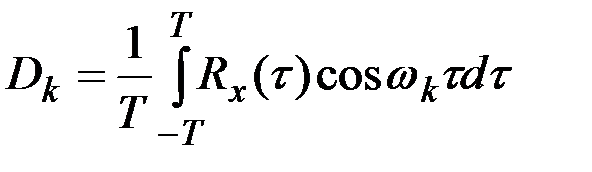 ,
, 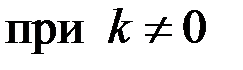 .
.
Имея в виду, что функции 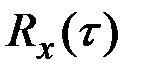 и
и 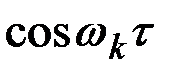 являются чётными, можно преобразовать последние формулы к виду
являются чётными, можно преобразовать последние формулы к виду
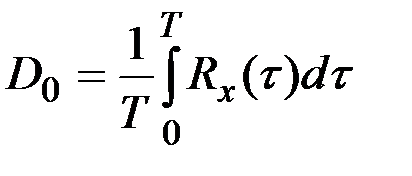 ;
; 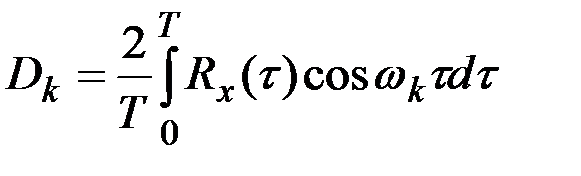 ,
, 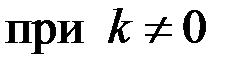 .
.
Перейдём в выражении корреляционной функции от аргумента 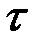 снова к двум аргументам
снова к двум аргументам 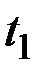 и
и 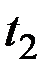 . Для этого положим
. Для этого положим
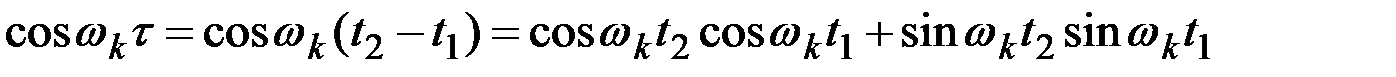 .
.
Тогда
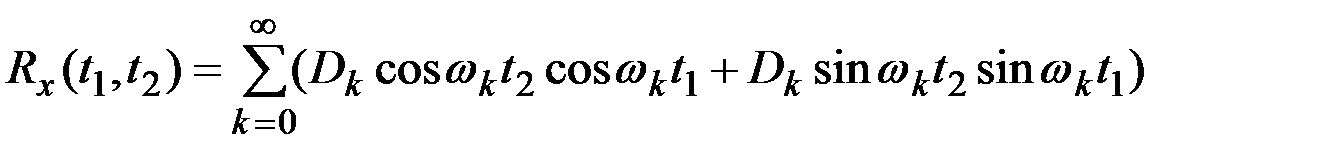 .
.
Это выражение представляет собой каноническое разложение корреляционной функции. Координатными функциями этого разложения являются попеременно косинусы и синусы частот, кратных 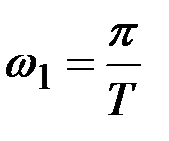 :
:
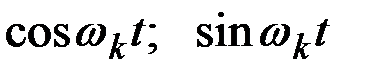
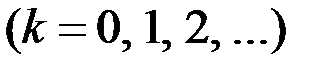 .
.
По каноническому разложению АКФ можно построить каноническое разложение самого случайного процесса с теми же координатными функциями и с дисперсиями, равными коэффициентам 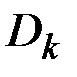 в разложении АКФ. Следовательно,
в разложении АКФ. Следовательно,
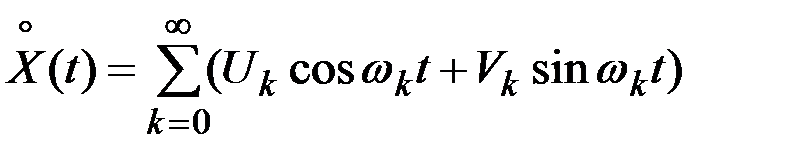 ,
,
где 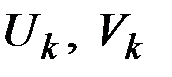 – некоррелированные СВ с математическими ожиданиями, равными нулю, и дисперсиями, одинаковыми для каждой пары СВ с одним и тем же индексом
– некоррелированные СВ с математическими ожиданиями, равными нулю, и дисперсиями, одинаковыми для каждой пары СВ с одним и тем же индексом 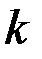 :
:
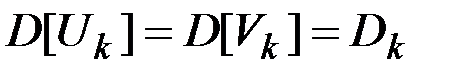 .
.
Таким образом, мы получили на интервале 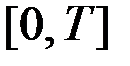 каноническое разложение процесса
каноническое разложение процесса 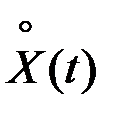 с координатными функциями
с координатными функциями 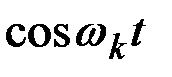 ;
; 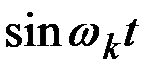 при различных частотах
при различных частотах 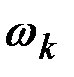 . Разложение такого рода называется спектральным разложением стационарного случайного процесса.
. Разложение такого рода называется спектральным разложением стационарного случайного процесса.
Спектральное разложение изображает стационарный процесс разложенным на гармонические колебания различных частот 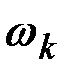 , причём амплитуды этих колебаний являются случайными величинами.
, причём амплитуды этих колебаний являются случайными величинами.
Определим дисперсию процесса.
По теореме о дисперсии линейной функции некоррелированных СВ
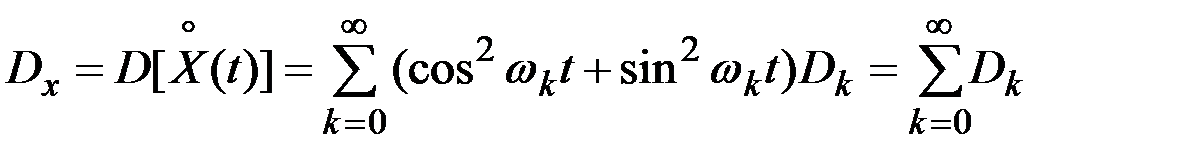 .
.
Дисперсия стационарного случайного процесса равна сумме дисперсий всех гармоник её спектрального разложения.
Распределение дисперсий по частотам изображается графически в виде спектра дисперсий. Сумма всех ординат спектра равна дисперсии процесса (рис.7.11).
Очевидно, что чем больший участок времени мы будем рассматривать, тем полнее будут наши сведения о процессе.
При 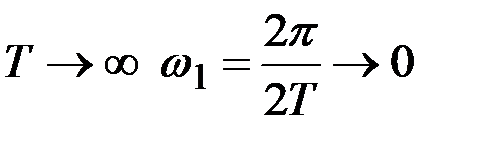 . Поэтому расстояния между частотами
. Поэтому расстояния между частотами 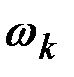 , на которых строится спектр, будут неограниченно уменьшаться.
, на которых строится спектр, будут неограниченно уменьшаться.
При этом дискретный (прерывистый, линейчатый) спектр будет приближаться к непрерывному, в котором каждому, сколь угодно малому интервалу частот 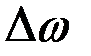 будет соответствовать элементарная дисперсия
будет соответствовать элементарная дисперсия 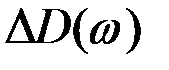 .
.

Рис.7.11. Дискретный спектр случайного процесса
Если откладывать по оси ординат среднюю плотность дисперсии, т.е. дисперсию, приходящуюся на единицу длины данного интервала частот, то получим ступенчатую диаграмму, напоминающую по принципу построения гистограмму статистического распределения.
Высота диаграммы на участке 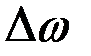 , прилежащем к точке
, прилежащем к точке 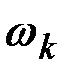 , равна
, равна 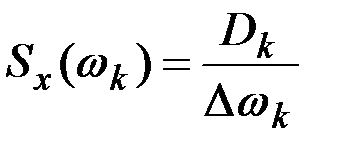 и представляет собой среднюю плотность дисперсии на этом участке.
и представляет собой среднюю плотность дисперсии на этом участке.
Суммарная площадь всей диаграммы равна дисперсии случайного процесса (рис.7.12).
При 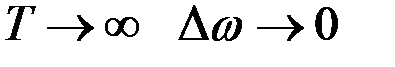 и ступенчатая кривая будет неограниченно приближаться к плавной кривой
и ступенчатая кривая будет неограниченно приближаться к плавной кривой 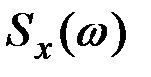 , которая называется спектральной плотностью дисперсии или просто спектральной плотностью процесса.
, которая называется спектральной плотностью дисперсии или просто спектральной плотностью процесса.
Тогда
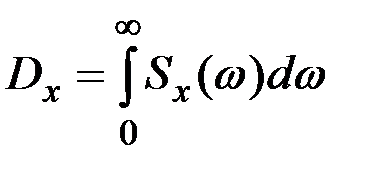 .
.
Спектральная плотность может быть выражена через корреляционную функцию.

Рис.7.12. Представление спектральной плотности процесса
Разделим выражение для 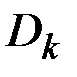 в каноническом разложении процесса на
в каноническом разложении процесса на 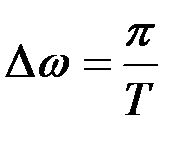 , получим
, получим
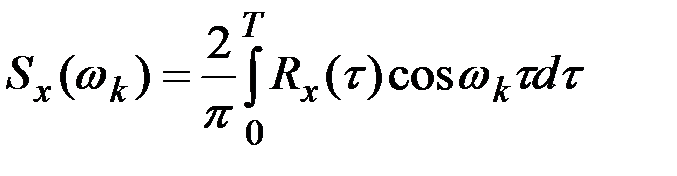 .
.
Так как 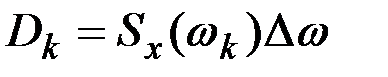 , то получим
, то получим
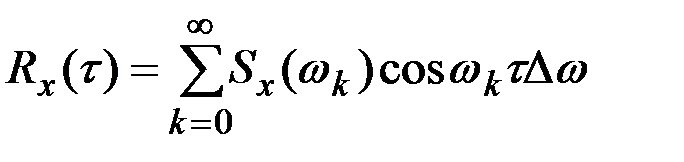 .
.
Очевидно, при 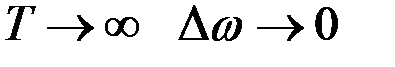 , дискретный аргумент
, дискретный аргумент 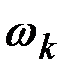 переходит в непрерывно меняющийся аргумент
переходит в непрерывно меняющийся аргумент  ; сумма переходит в интеграл по переменной
; сумма переходит в интеграл по переменной  ; средняя плотность дисперсии
; средняя плотность дисперсии 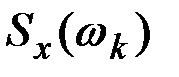 стремится к плотности дисперсии
стремится к плотности дисперсии 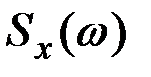 и, в итоге получаем:
и, в итоге получаем:
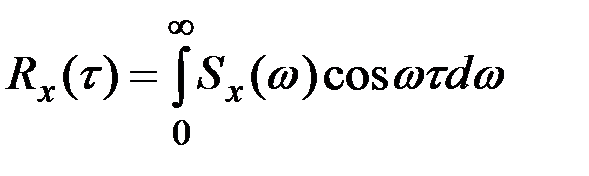 ,
,
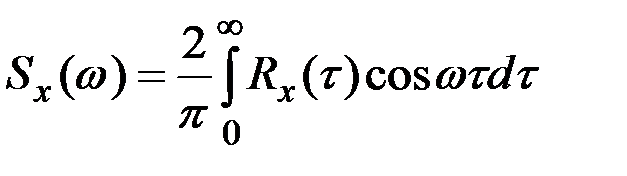 .
.
Спектральная плотность случайного процесса (автоспектр) описывает общую частотную структуру процесса через спектральную плотность дисперсии его значений.
Технически дисперсию значений реализации в интервале частот 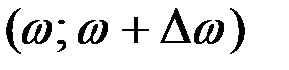 можно получить, подавая эту реализацию на вход полосового фильтра с узкой полосой пропускания и усредняя возведённую в квадрат функцию на выходе фильтра:
можно получить, подавая эту реализацию на вход полосового фильтра с узкой полосой пропускания и усредняя возведённую в квадрат функцию на выходе фильтра:
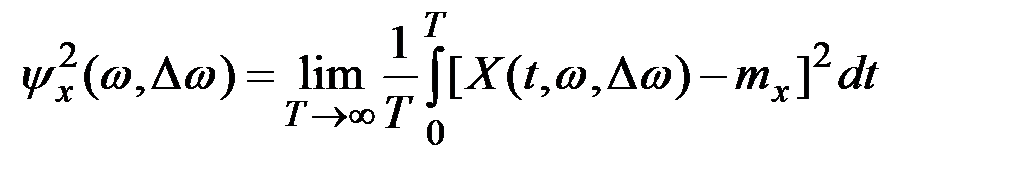 .
.
Здесь 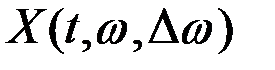 – составляющие
– составляющие 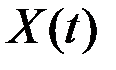 , имеющие частоты в интервале
, имеющие частоты в интервале 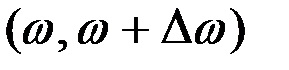 .
.
Спектральная плотность тогда определяется как предел
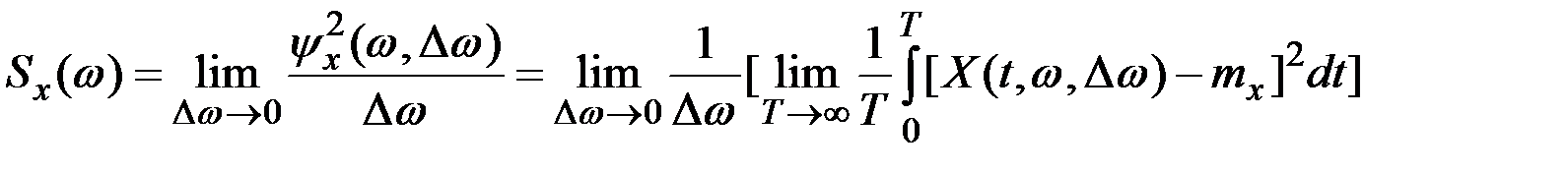 .
.
Величина 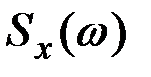 всегда действительная, неотрицательная функция.
всегда действительная, неотрицательная функция.
Конечное значение спектральной плотности на нулевой частоте означает, что в состав случайного процесса в качестве слагаемого входит обычная случайная величина с соответствующей дисперсией.
Дисперсия процесса определяется площадью под кривой спектральной плотности как функции частоты
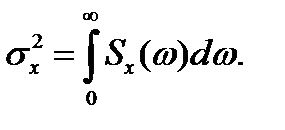 .
.
Нормированная спектральная плотность определяется выражением
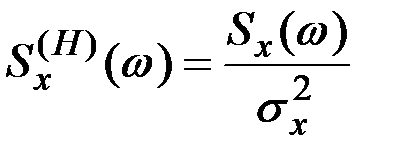 .
.
Площадь под кривой 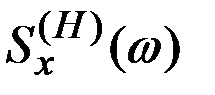 равна единице.
равна единице.
В ряде случаев с точки зрения простоты математических преобразований оказывается удобным пользоваться не действительной, а комплексной формой записи как спектрального разложения процесса, так и его характеристик.
Комплексная форма записи удобна, в частности, потому, что всевозможные линейные операции над функциями, имеющими вид гармонических колебаний (дифференцирование, интегрирование, решение линейных дифференциальных уравнений и т.д.), осуществляется гораздо проще, когда эти гармонические колебания записаны не в виде синусов и косинусов, а в комплексной форме, в виде показательных функций.
Комплексная форма записи корреляционной функции и спектральной плотности применяется и в тех случаях, когда сам процесс (а следовательно и его корреляционная функция, и спектральная плотность) действителен.
Связь между гармоническими и показательными функциями осуществляется известными соотношениями (формулами) Эйлера:
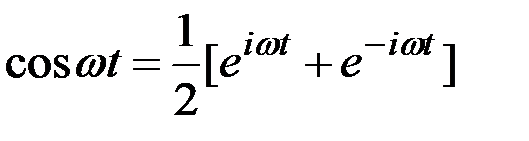 ;
; 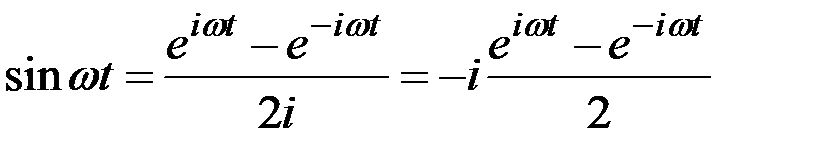 .
.
Используя эти выражения учитывая, что 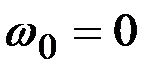 будем иметь разложение с координатными функциями
будем иметь разложение с координатными функциями 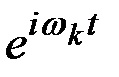 ,
, 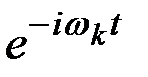
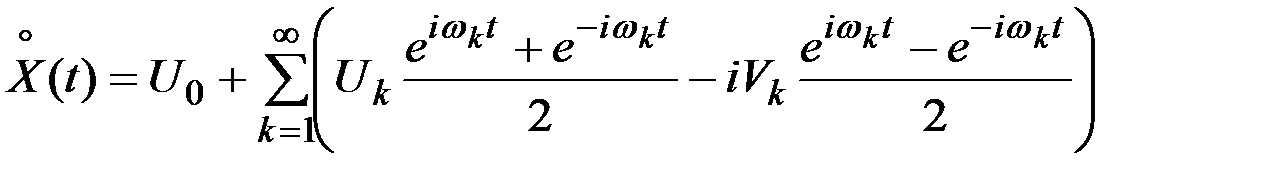 .
.
Преобразуем это разложение так, чтобы в нём в качестве координатных функций фигурировали только функции 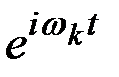 .
.
Для этого распространим условно область частот на отрицательные значения и в качестве частот спектрального разложения будем рассматривать значения 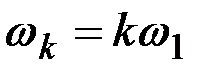
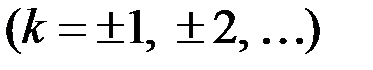 , т.е. будем считать, что k принимает не только положительные, но и отрицательные значения.
, т.е. будем считать, что k принимает не только положительные, но и отрицательные значения.
Тогда можно записать, положив 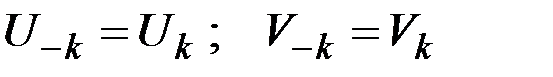 :
:
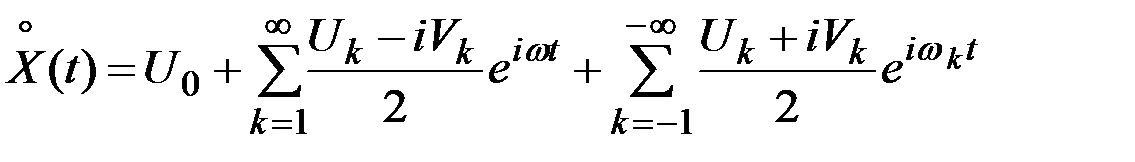 .
.
Это разложение случайного процесса 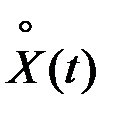 по координатным функциям
по координатным функциям 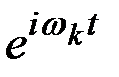 , а коэффициенты представляют собой комплексные случайные величины. Обозначая их через
, а коэффициенты представляют собой комплексные случайные величины. Обозначая их через 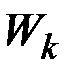
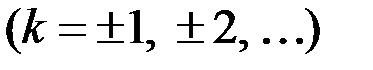 , можно записать
, можно записать
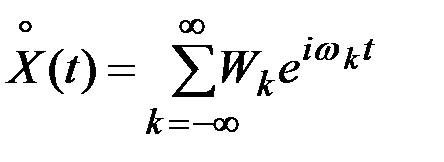 ,
,
где 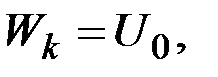 при
при 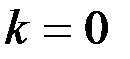 ,
,
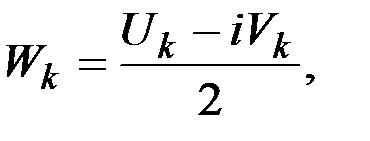 при
при 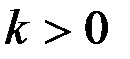 ,
,
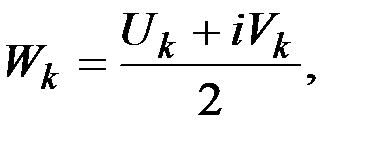 при
при 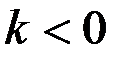 .
.
Можно показать, что коэффициенты этого разложения не коррелированны между собой, а, следовательно, имеем каноническое разложение.
Очевидно:
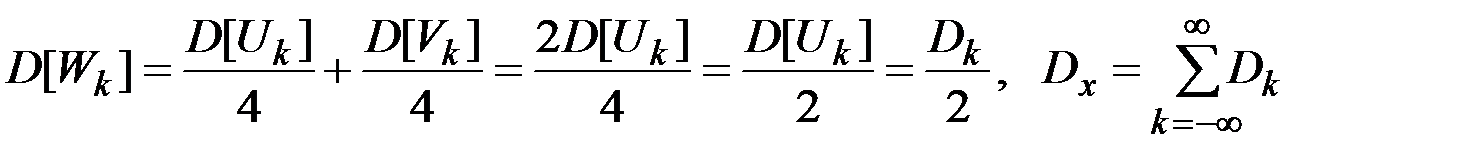 .
.
Обозначим: 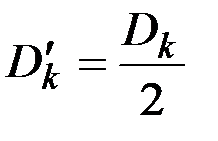 при
при 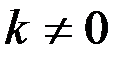 ;
; 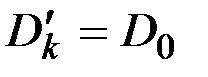 при
при 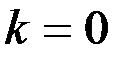 .
.
Если построить дискретный спектр процесса 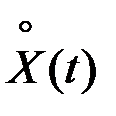 с распространением частот на отрицательную область, то он будет симметричным относительно оси координат. От ранее построенного спектра он отличается тем, что определён не только для положительных, но и для отрицательных частот, но зато его ординаты при
с распространением частот на отрицательную область, то он будет симметричным относительно оси координат. От ранее построенного спектра он отличается тем, что определён не только для положительных, но и для отрицательных частот, но зато его ординаты при 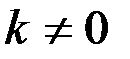 (при
(при 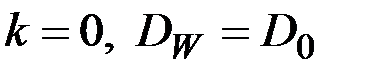 ) вдвое меньше соответствующих ординат прежнего спектра.
) вдвое меньше соответствующих ординат прежнего спектра.
Корреляционная функция процесса, заданного каноническим разложением, определяется соотношением
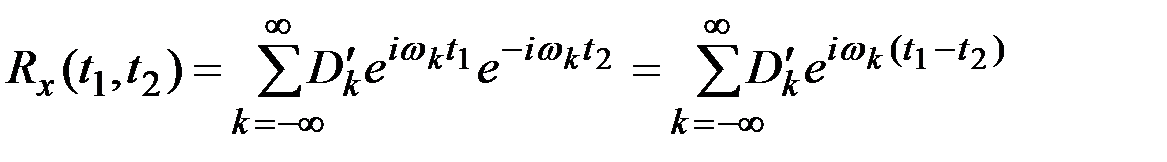 .
.
Переходя к аргументу 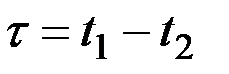 , имеем:
, имеем:
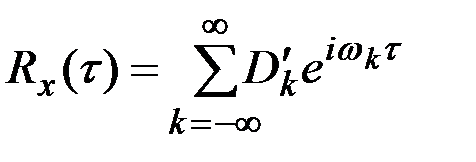 ,
,
где 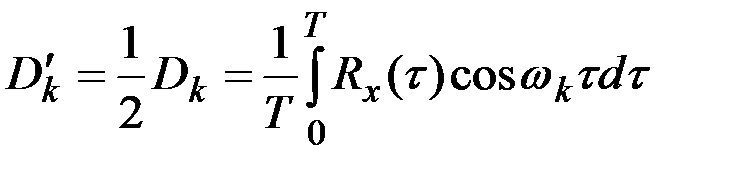 при
при 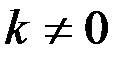 .
.
Придадим последнему выражению также комплексную форму, используя формулу Эйлера для косинуса
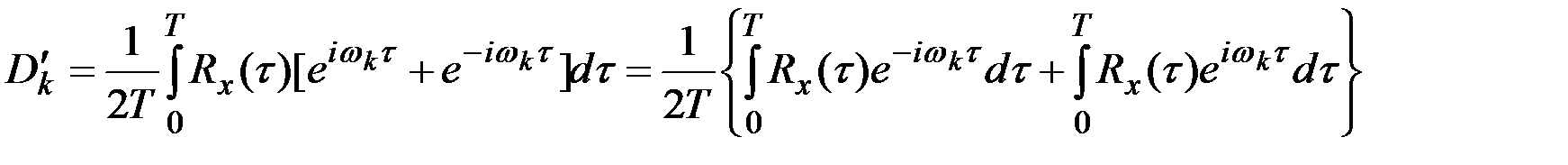 .
.
Полагая во втором интеграле 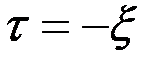 , имеем
, имеем
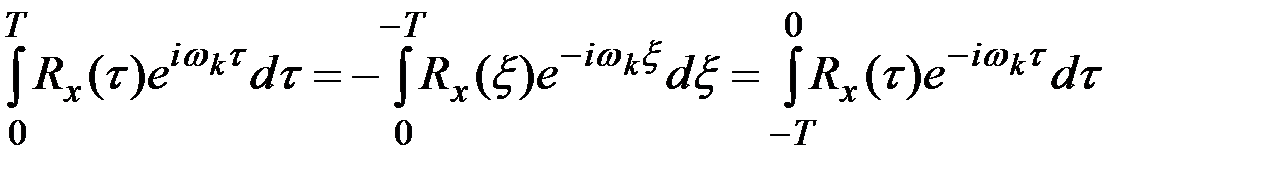 .
.
Отсюда получаем:
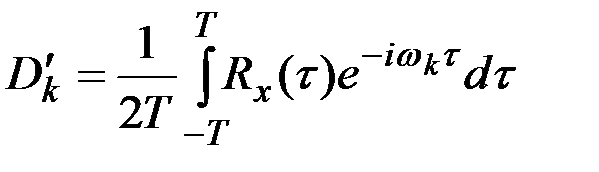 .
.
При 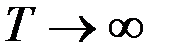 , вводя в рассмотрение спектральную плотность в виде предела
, вводя в рассмотрение спектральную плотность в виде предела 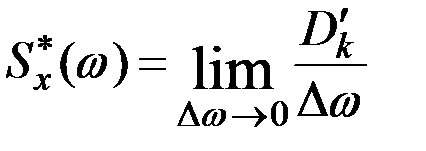 , получаются соотношения, связывающие корреляционную функцию и спектральную плотность в комплексной форме:
, получаются соотношения, связывающие корреляционную функцию и спектральную плотность в комплексной форме:
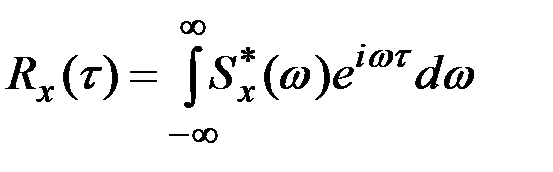 ,
, 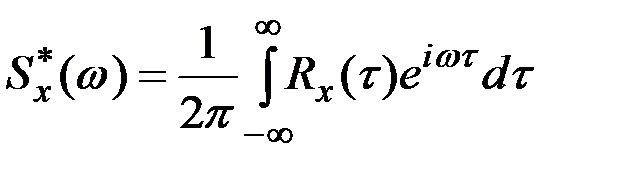 .
.
Последние формулы могут быть получены и непосредственно из формул 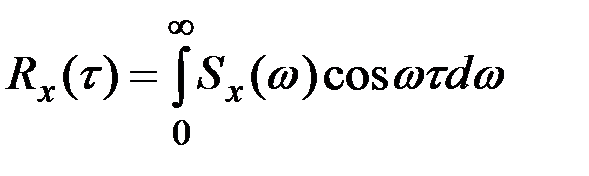 и
и 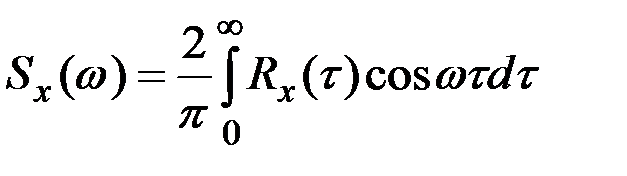 , если произвести в них замену
, если произвести в них замену 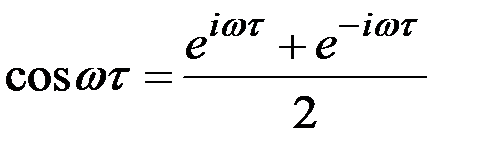 , положить
, положить 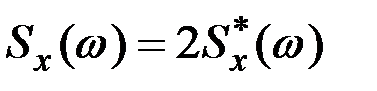 и расширить область интегрирования на интервал от
и расширить область интегрирования на интервал от 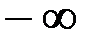 до
до 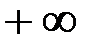 .
.
Если изобразить обе функции спектральной плотности 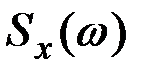 и
и 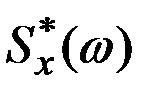 на графике, то они различаются только масштабом по оси ординат и тем, что функция
на графике, то они различаются только масштабом по оси ординат и тем, что функция 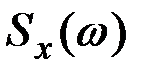 для отрицательных частот не определена. Ординаты функции
для отрицательных частот не определена. Ординаты функции 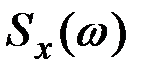 вдвое меньше (рис.7.13).
вдвое меньше (рис.7.13).

Рис.7.13. Действительная и комплексная формы
спектральной плотности
На практике в качестве спектральной плотности применяется как действительная так и комплексная формы.
Если применять не круговую частоту ω, а частоту колебаний f, выраженную в герцах 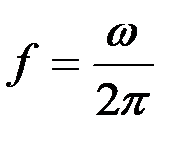 , то подстановкой
, то подстановкой 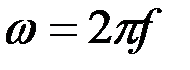 последние формулы приводятся к виду
последние формулы приводятся к виду
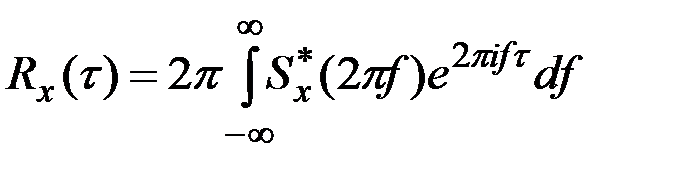 ,
, 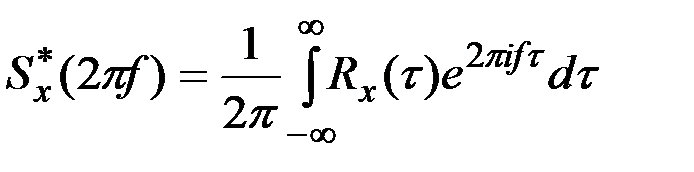 .
.
На практике используется как круговая, так и циклическая частоты.
В табл.7.3 приведено соответствие наиболее часто встречаемых на практике выражений корреляционных функций и спектральных плотностей случайных процессов.
Таблица 7.3
Соответствие корреляционных функций
и спектральных плотностей случайных процессов
| | 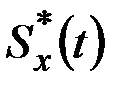
| |
| 1 | 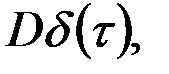 где
где 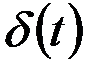 – дельта–функция – дельта–функция
| 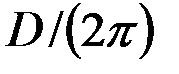
|
| 2 | 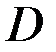
| 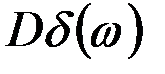
|
| 3 | 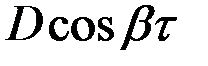
| 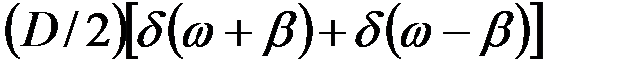
|
| 4 | 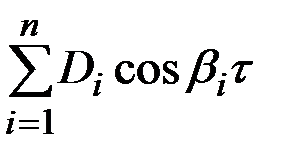
| 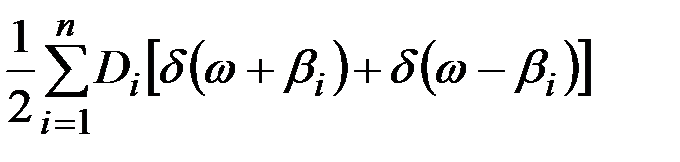
|
| 5 | 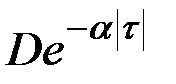
| 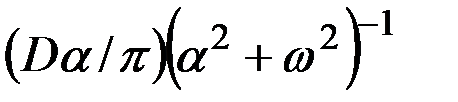
|
| 6 | 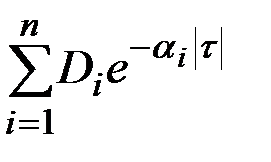
| 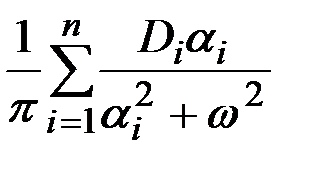
|
| 7 | 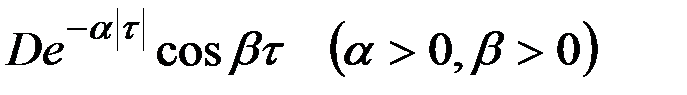
| 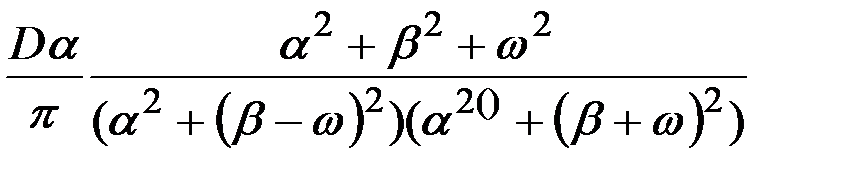
|
| 8 | 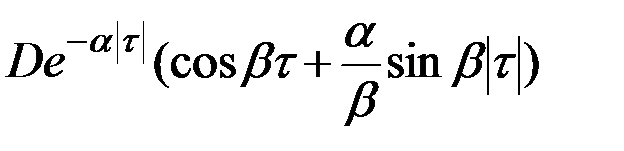
| 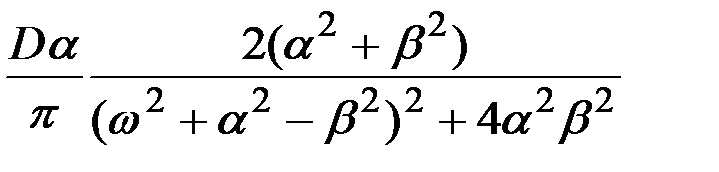
|
| 9 | 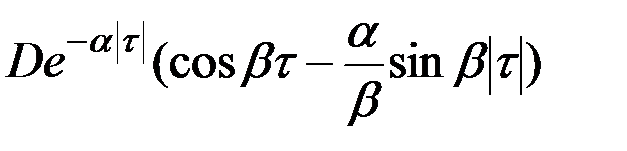
| 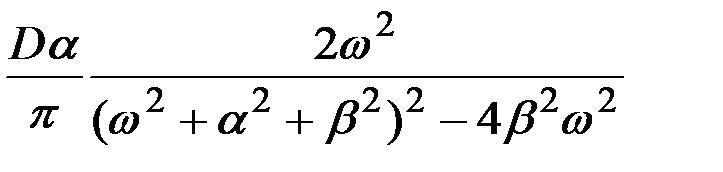
|
| 10 | 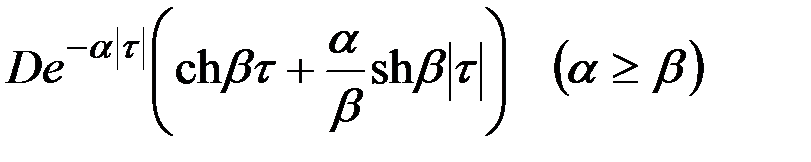
| 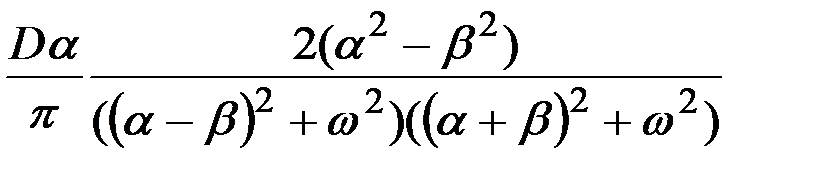
|
| 11 | 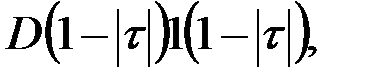 где
где 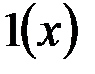 – единичная функция – единичная функция
| 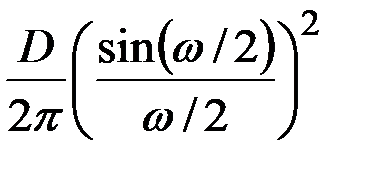
|
| 12 | 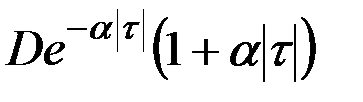
| 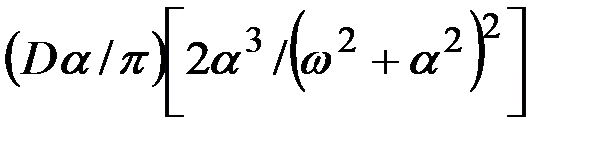
|
| 13 | 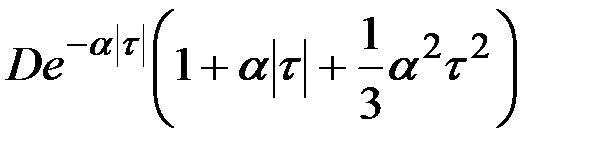
| 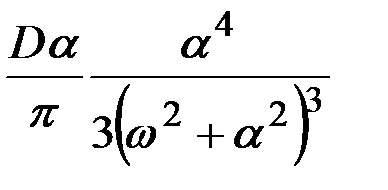
|
| 14 | 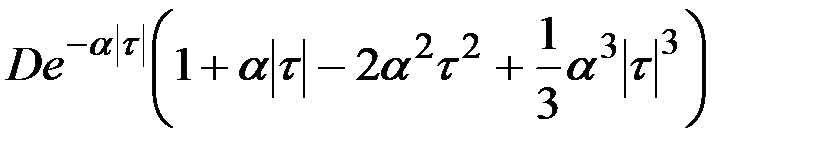
| 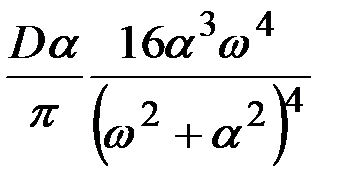
|
| 15 | 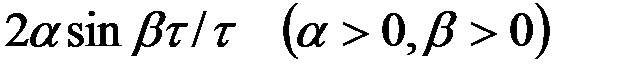
| 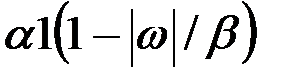
|
| 16 | 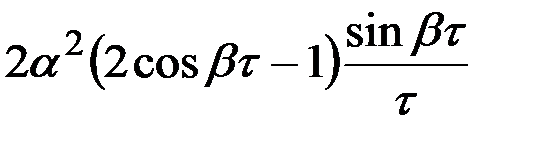
| 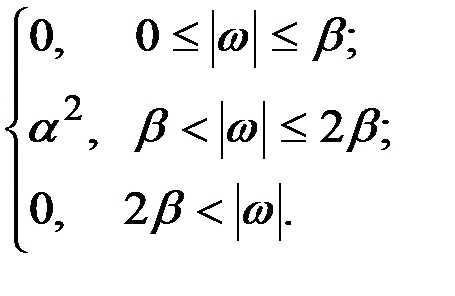
|
| 17 | 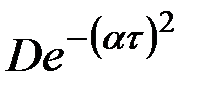
| 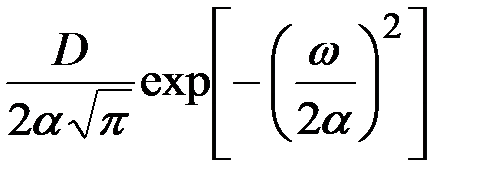
|
| 18 | 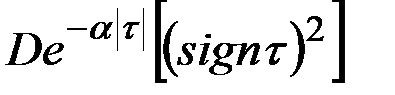
| 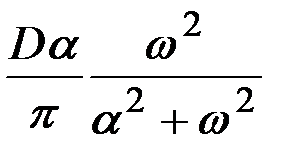
|
Пример 7.21. Может ли быть при каких–либо значениях аргументов:
1) Функция распределения процесса больше единицы?
2) Плотность распределения процесса больше единицы?
3) Функция распределения процесса отрицательной?
4) Плотность распределения процесса отрицательной?
5) Дисперсия процесса больше единицы?
6) Среднеквадратичное отклонение процесса меньше нуля?
7) Корреляционная функция процесса отрицательной?
8) Спектральная плотность процесса отрицательной?
9) Нормированная корреляционная функция процесса равна нулю?
Решение. 1) нет; 2) да; 3) нет; 4) нет; 5) да; 6) нет; 7) да; 8) нет; 9) да.
Пример 7.22. Как изменятся основные характеристики случайного процесса, если: 1) его значения умножить на постоянную величину a;
2) к процессу добавить постоянную величину a?
Решение.
1) Математическое ожидание умножится на a; дисперсия увеличится в a2 раз; среднеквадратическое отклонение умножится на ½a½; корреляционная функция увеличится в a2 раз; спектральная плотность умножится на a2; функция плотности в a раз увеличит масштаб по оси абсцисс и в a раз уменьшит масштаб по оси ординат.
2) К математическому ожиданию добавится величина a; график функции плотности сдвигается влево на a единиц, если a < 0, или на a единиц вправо, если a > 0; другие характеристики не изменятся.
Пример 7.23. Показать, что стационарный «белый шум» Х (t) имеет постоянную спектральную плотность.
Решение. У стационарного белого шума 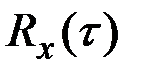 = c d (t).
= c d (t).
Отсюда 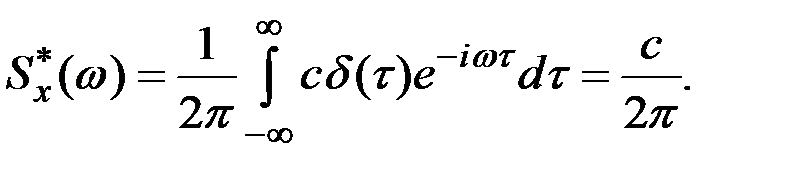
Величина с называется интенсивностью белого шума.
Стационарный белый шум представляет собой случайные колебания на всех частотах. При этом дисперсия этих колебаний, приходящихся на элементарный участок D w, остаётся постоянной и не зависит от частоты колебаний w. Эта дисперсия не зависит от частоты w и будет приближённо равна величине
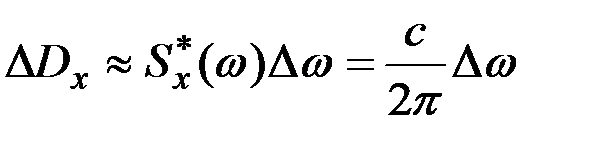 .
.
Пример 7.24. Корреляционная функция процесса определяется выражением 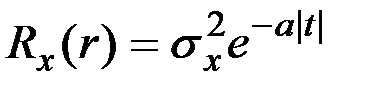 , где a > 0. Определить спектральную плотность процесса.
, где a > 0. Определить спектральную плотность процесса.
Решение. Воспользуемся следующим соотношением
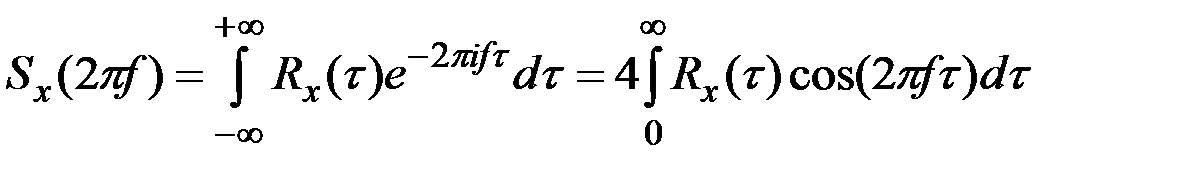 .
.
Имеем
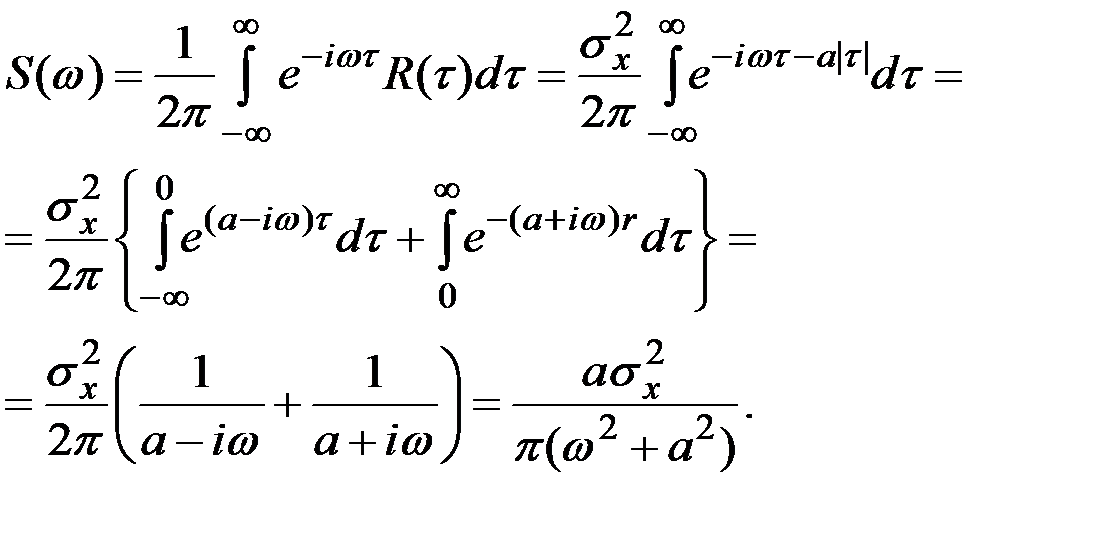
Пример 7.25. Нормированная АКФ процесса убывает по линейному закону от единицы до нуля. Определить нормированную спектральную плотность процесса.
Решение. Корреляционная функция выражается формулой
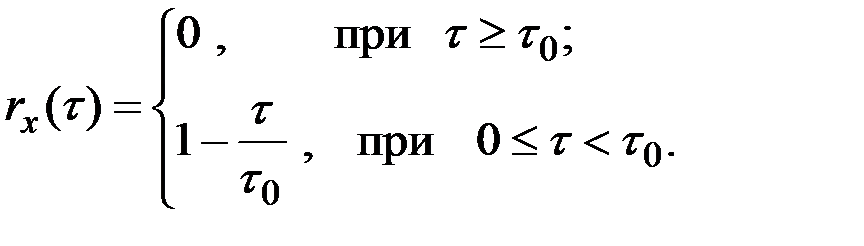
Нормированную спектральную плотность получим из соотношения
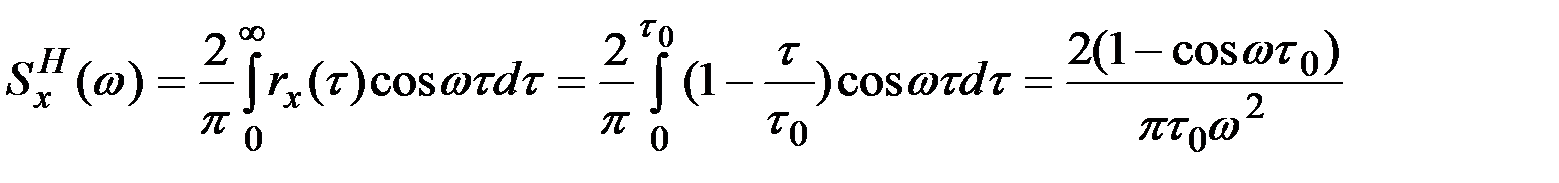 .
.
Первый (абсолютный) максимум спектральной плотности достигается при w = 0. Раскрытием неопределённости в этой точке убеждаемся, что он равен t0 / p. Изменение t0 равносильно изменению масштаба кривой 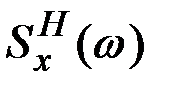 по обеим осям при сохранении её единичной площади.
по обеим осям при сохранении её единичной площади.
Пример 7.26. Спектральная плотность изменения температуры воздуха в летний период (температура фиксировалась ежедневно в 12.00 часов) выражается зависимостью 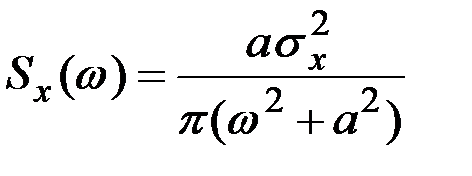 . Определить корреляционную функцию этого процесса.
. Определить корреляционную функцию этого процесса.
Решение. Пользуясь преобразованием Фурье, имеем
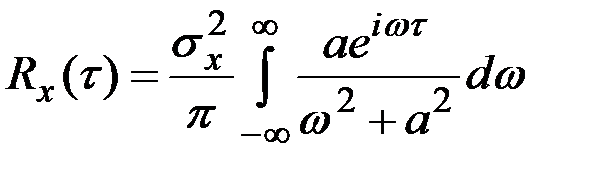 .
.
Для вычисления этого интеграла применим теорию вычетов.
При t > 0 интеграл 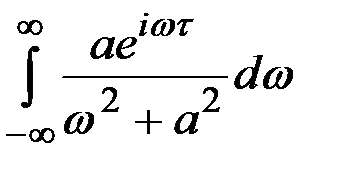 равняется интегралу, взятому по контуру, составленному из вещественной оси и замкнутой полуокружности бесконечного радиуса, расположенной в верхней полуплоскости.
равняется интегралу, взятому по контуру, составленному из вещественной оси и замкнутой полуокружности бесконечного радиуса, расположенной в верхней полуплоскости.
Поэтому его значение равно вычету относительно единственного полюса w = ia, умноженному на 2p a, т.е.
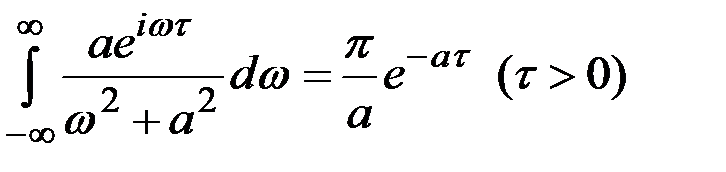 .
.
Аналогично при t < 0, замыкая вещественную ось через нижнюю полуплоскость, получаем 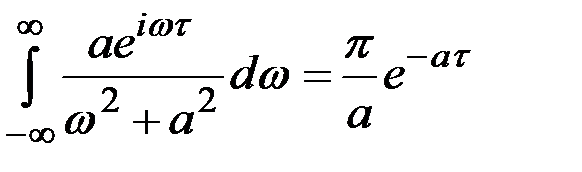 .
.
Следовательно, при любом знаке t получим: