Здесь взято среднее значение по интервалу , так как функции x(t) и x(t + τ) известны вместе только в этом интервале.
Последней формулой рекомендуется пользоваться при 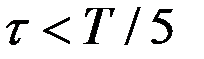 .
.
При больших значениях τ погрешность оценки корреляционной функции увеличивается.
Если R(τ) ® 0 при 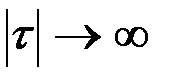 , то это обычно является достаточном условием для того, чтобы математическое ожидание функции можно было определять как среднее по времени.
, то это обычно является достаточном условием для того, чтобы математическое ожидание функции можно было определять как среднее по времени.
Если стационарная СФ к тому же нормально распределена, то неограниченное убывание корреляционной функции R(τ) при 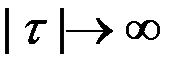 является условием, достаточным для того, чтобы определить корреляционную функцию по одной реализации.
является условием, достаточным для того, чтобы определить корреляционную функцию по одной реализации.
На практике об эргодичности процесса судят на основании физических соображений, связанных с природой изучаемого процесса. Если процесс внутренне неоднороден и его можно разложить на более элементарные процессы, то он описывается только неэргодическими СФ. Наоборот, внутренняя однородность процесса говорит об его эргодичности.
Например, процесс обработки поверхности детали при соблюдении одних и тех же основных условий от опыта к опыту описывается эргодической стационарной СФ. Но если рассматривать процесс обработки поверхности в зависимости от скорости работы инструмента, т.е. от опыта к опыту менять скорость работы инструмента, то, очевидно, что такой процесс уже не будет внутренне однородным, и хотя он ещё остается стационарным, но свойством эргодичности обладать не будет.
Не обладает свойством эргодичности также периодическая стационарная СФ и стационарная СФ, имеющая периодическую составляющую.
При решении практических задач в результате опыта, как правило, оказываются известными значения реализации x(t) для конечного множества значений аргумента и при вычислении характеристик эргодической стационарной СФ интегралы заменяют конечными суммами.
Для некоторых типов процессов корреляционная функция может быть вычислена исходя из его физической сути как, например, для процесса типа “телеграфный сигнал”.
“Телеграфный сигнал” x(t) принимает значения a и – а, причём переход от значения к значению совершается в случайные моменты 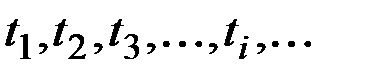 , образующие простейший поток.
, образующие простейший поток.

Рис.7.5. Случайный процесс в виде «телеграфного сигнала»
В силу свойств простейшего потока вероятность за время τ совершиться m переходам подчинена распределению Пуассона и равна
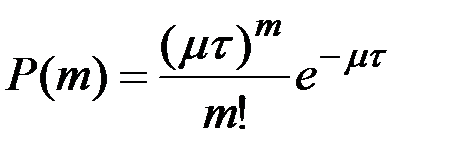 ,
,
где m – интенсивность перехода системы из состояния в состояние.
Корреляционная функция 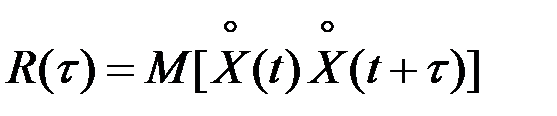 вычисляется как математическое ожидание произведения
вычисляется как математическое ожидание произведения 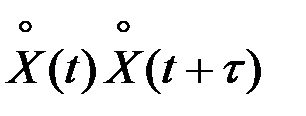 , принимающего значения
, принимающего значения  , если число переходов чётно, и –
, если число переходов чётно, и – 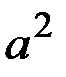 , если число переходов нечётно:
, если число переходов нечётно:
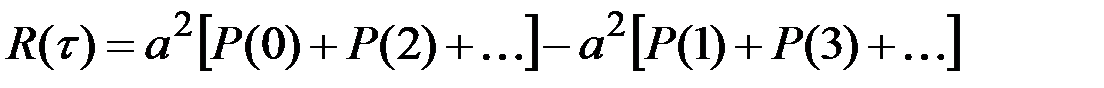 .
.
Здесь в квадратных скобках записаны вероятности совершения чётного и нечётного числа переходов за время τ.
Подставляя эти вероятности P(m) в АКФ, получим
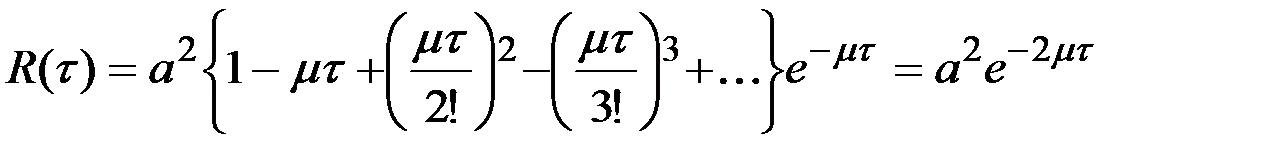 .
.
Так как сумма в скобках равна 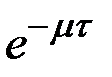 , то
, то
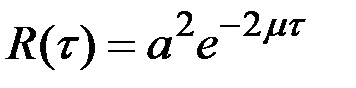 ,
, 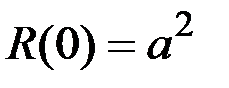 .
.
Одним из важных для практических расчётов параметров СФ является "интервал корреляции" – время 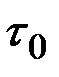 , в течение которого между сечениями процесса сохраняется статистическая связь и корреляционный момент находится в определённых пределах, например |R(τ)| > 0,05.
, в течение которого между сечениями процесса сохраняется статистическая связь и корреляционный момент находится в определённых пределах, например |R(τ)| > 0,05.
Иногда время корреляции определяют как половину ширины основания прямоугольника единичной высоты, площадь которого равна площади под кривой модуля корреляционной функции:
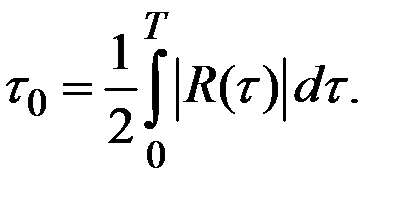 .
.
Процесс, интервал корреляции которого равен нулю, являлся бы "абсолютно случайным" – связей между его сечениями не было бы вовсе.
Реально такой процесс не существует, однако как математическая модель он оказывается исключительно полезным в самых разнообразных исследованиях и носит название "белый шум".
В технических системах протекают случайные процессы, имеющие весьма различные времена корреляции. Так, например, для рабочих процессов мощного энергоблока тепловой электростанции флюктуации (изменения) яркости факела в топке имеют интервал корреляции в доли секунды; в минуты – температуры перегретого пара; десятки минут – нагрузки генератора и расхода топлива и, наконец, десятки суток – теплотворной способности твердого топлива. Ясно, что случайное изменение яркости пламени (важная характеристика режима горения) по сравнению с колебаниями теплотворной способности представляет собой очень хорошее подобие “белого шума”.
Плотность распределения (закон распределения) случайного эргодического стационарного процесса определяет вероятность того, что значения процесса в произвольный момент времени будут заключены в определенном интервале (рис.7.6).
Вероятность того, что значения X(t) попадают в интервал от x до 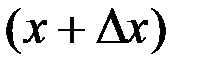 можно найти, вычисляя отношение
можно найти, вычисляя отношение 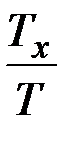 , где
, где 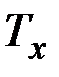 – суммарная продолжительность нахождения процесса в интервале
– суммарная продолжительность нахождения процесса в интервале 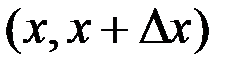 за время наблюдения T:
за время наблюдения T:
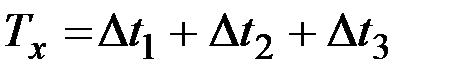 ;
; 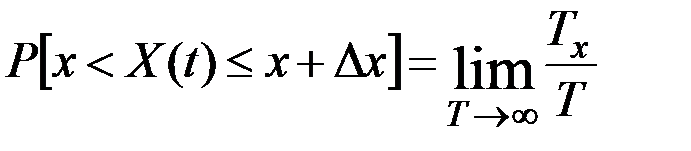 .
.
Тогда
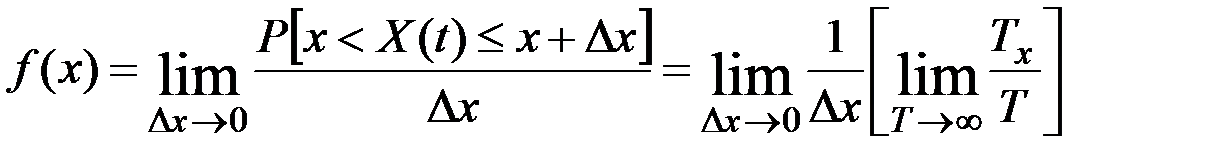 .
.
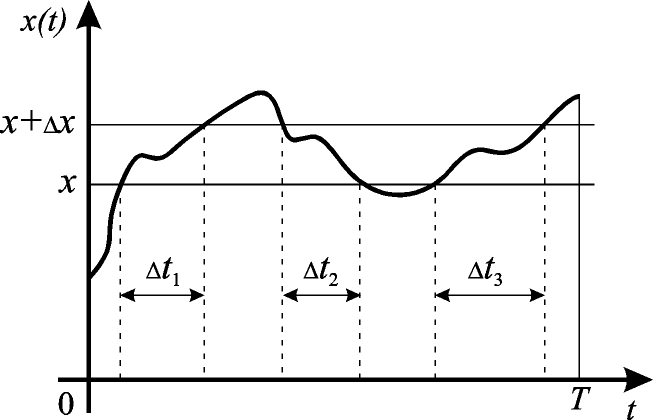
Рис.7.6. Определение плотности распределения
эргодического процесса
Функция f(x) всегда действительная неотрицательная функция.
Вероятность того, что мгновенное значение стационарного процесса X(t) не превышает некоторой величины x, характеризуется функцией распределения F(x|t) (иначе кумулятивной, интегральной функцией распределения):
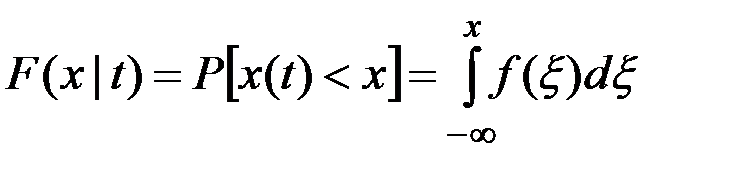 .
.
Функция распределения ограничена значениями ноль и единица, так как вероятность того, что X(t) меньше 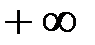 , равна единице.
, равна единице.
Вероятность попадания X(t) в некоторый интервал 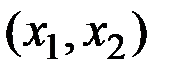 определяется по формуле
определяется по формуле
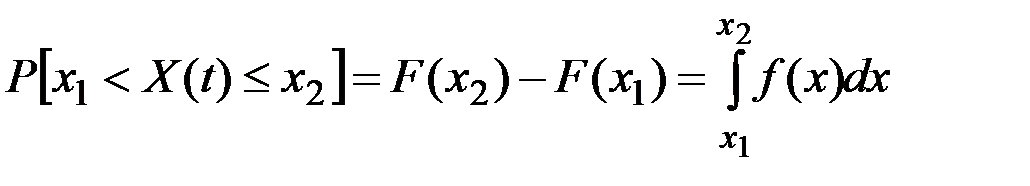 .
.
Напомним, что 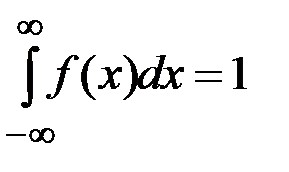 .
.
Основная цель получения плотности распределения физического процесса состоит в установлении вероятностных законов для его мгновенных значений.
Эту функцию можно использовать также и для того, чтобы отличить гармонический процесс от случайного.
Плотность распределения позволяет опытному специалисту выявить нелинейные физические эффекты.
Для эргодических процессов функцию одномерной плотности можно получить по следующему алгоритму.
Рассмотрим n значений 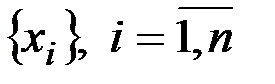 реализации x(t) стационарного случайного процесса.
реализации x(t) стационарного случайного процесса.
Пусть k – число разрядов, которые охватывают весь диапазон 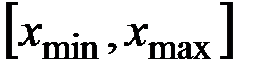 изменения функции (процесса).
изменения функции (процесса).
Ширина каждого разряда
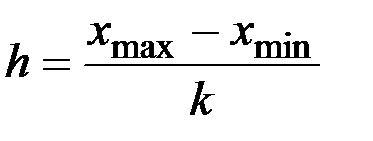 .
.
Верхняя граница j–го разряда
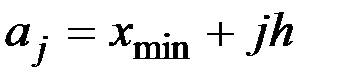 ,
, 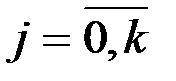 .
.
Определим теперь последовательность из k + 2 чисел 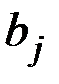 из условий:
из условий:
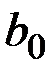 – число значений
– число значений 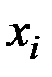 , удовлетворяющих неравенству
, удовлетворяющих неравенству
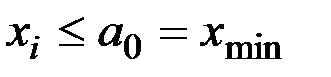 ,
, 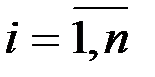 ;
;
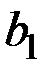 – число значений
– число значений 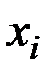 , удовлетворяющих неравенству
, удовлетворяющих неравенству
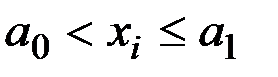 ;
;
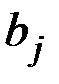 – число значений
– число значений 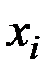 , удовлетворяющих неравенству
, удовлетворяющих неравенству
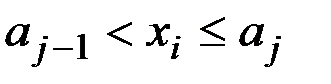 ;
;
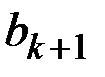 – число значений
– число значений 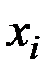 , удовлетворяющих неравенству
, удовлетворяющих неравенству
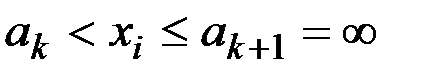 .
.
В результате n значений последовательности 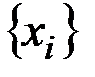 будут отсортированы таким образом, что
будут отсортированы таким образом, что
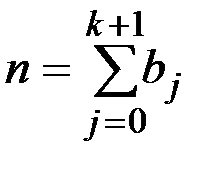 .
.
Тогда плотность распределения функции X(t) можно оценить в виде
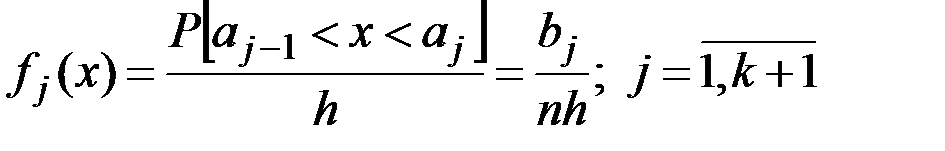 .
.
Функция плотности вероятностей эргодического процесса отражает только статистические свойства процесса, но не характеризует динамику процесса, которую можно описать корреляционной функцией.
7.3. Система случайных функций
Для описания совместных характеристик реализаций двух случайных процессов используют:
– совместную плотность распределения,
– взаимную корреляционную функцию (ВКФ).
Они дают информацию о совместных характеристиках процессов в амплитудной и временной областях.
Совместная плотность распределения двух СФ определяет вероятность того, что их ординаты в произвольный момент времени будут заключены одновременно в двух определённых интервалах их значений.
Для эргодических процессов совместная плотность распределения
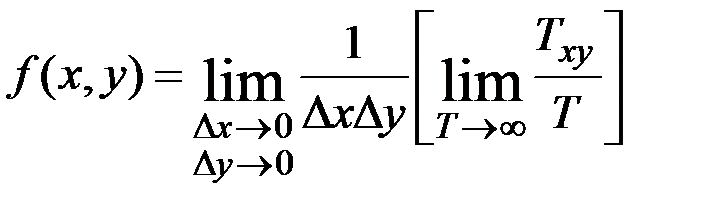 ,
,
где Txy – суммарная продолжительность одновременного нахождения значений процессов X(t) и Y(t) в интервалах 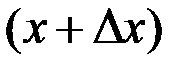 и
и 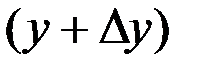 соответственно за время наблюдения Т.
соответственно за время наблюдения Т.
Вероятность того, что мгновенные значения X(t) и Y(t) не превышают некоторых величин x и y характеризуется совместной функцией распределения
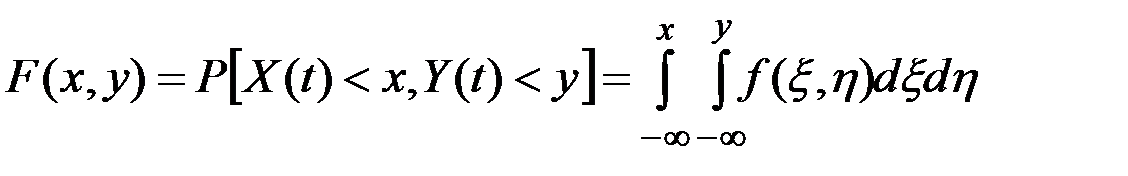 .
.
Когда два рассматриваемых процесса статистически независимы, то 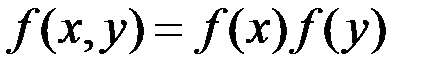 , а в общем случае
, а в общем случае
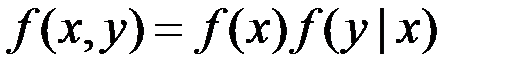 .
.
Совместная плотность распределения применяется для вероятностного описания явления, которое характеризуется двумя процессами, связанными как–то между собой, например, для прогноза числа соударения двух упругих конструкций, случайные колебания которых частично зависят друг от друга.
Иногда находят связь между вероятностью осуществления двух событий и вероятностью осуществления одного из них.
Для определения условных вероятностей также необходимо знать совместную плотность распределения.
Эта функция используется также при прогнозе распределения пиковых значений и экстремальных величин при вычислении ожидаемого числа пересечений нулевого или произвольного порогового уровня некоторым физическим процессом.
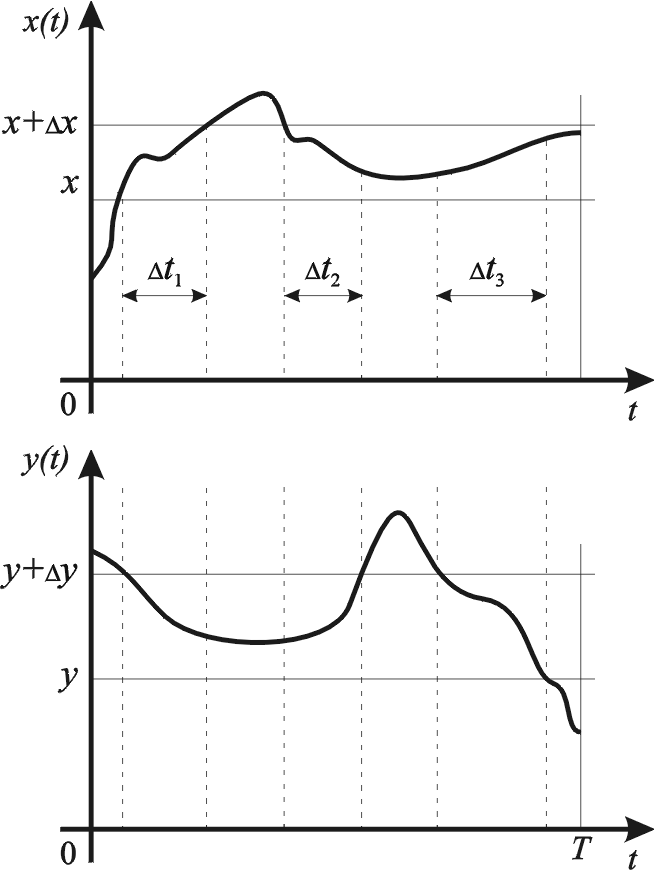
Рис.7.7. Определение совместной плотности распределения
Взаимная корреляционная функция двух процессов характеризует общую зависимость значений одного процесса от значения другого:
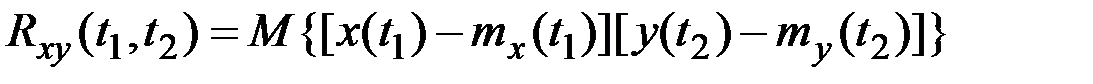 .
.
Имеет место соотношение
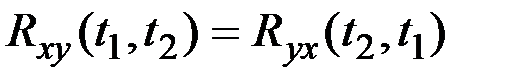 .
.
Процессы X(t) и Y(t) называются некоррелированными, если их ВКФ 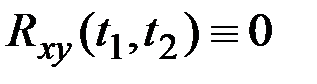 для всех
для всех 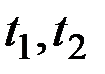 .
.
Нормированной ВКФ называется функция
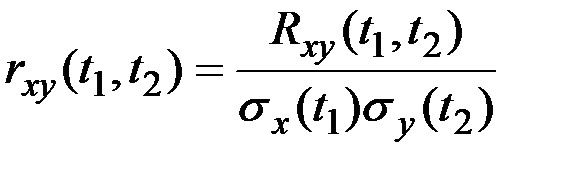 .
.
Эта величина всегда заключена в пределах от –1 до +1.
Для стационарно связанных двух процессов
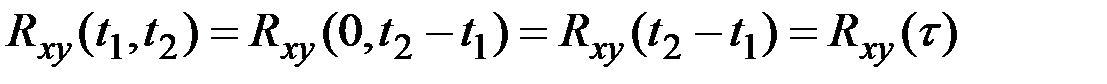 .
.
Величина 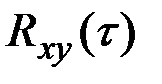 – всегда действительная функция, которая может быть как положительной, так и отрицательной.
– всегда действительная функция, которая может быть как положительной, так и отрицательной.
ВКФ не обязательно имеет максимум в точке τ = 0 и не обязательно является чётной, как это было в случае АКФ.
Свойства ВКФ:
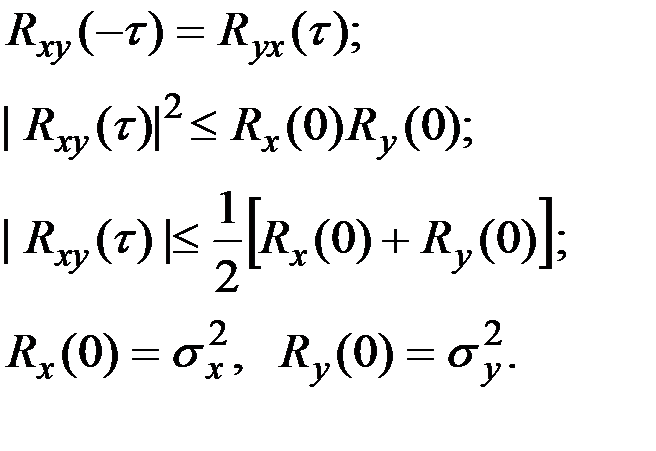
Оценку ВКФ можно получить непосредственным вычислением:
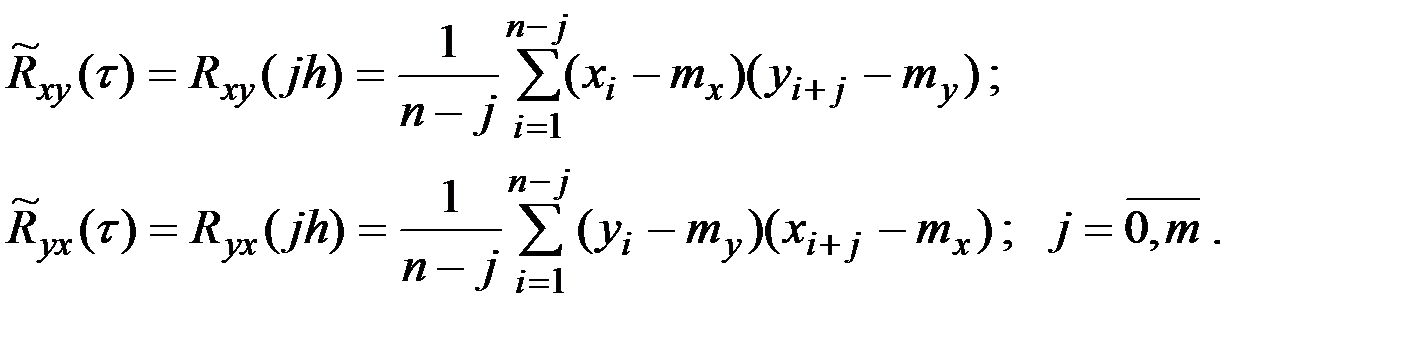
Здесь h – шаг дискретизации процесса.
Двумерная функция плотности для двух эргодических процессов получается по следующему алгоритму.
Пусть имеем 2 реализации
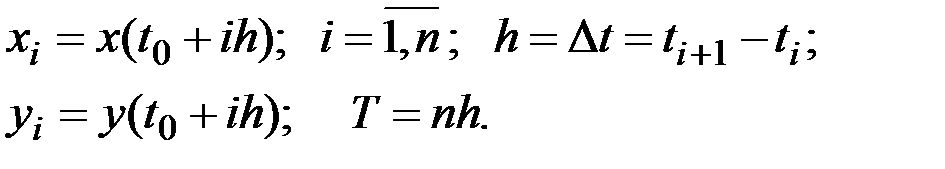
Вначале вычисляются средние значения реализаций процессов
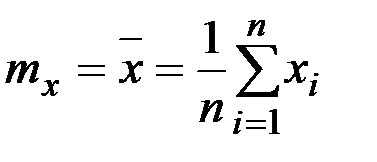 ;
; 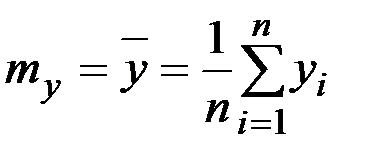 .
.
Затем производится центрирование величин
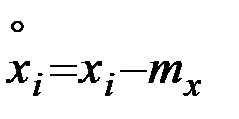 ;
; 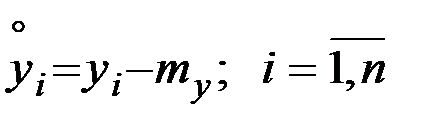 .
.
Тогда оценку совместной плотности распределения реализаций x(t) и y(t) можно найти в виде
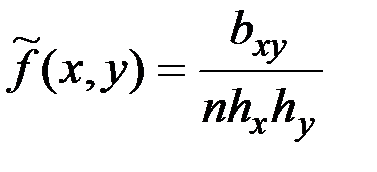 ,
,
где 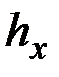 и
и 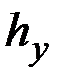 – узкие интервалы с центральными значениями x и y соответственно; а
– узкие интервалы с центральными значениями x и y соответственно; а 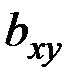 – число пар отсчётов, которые одновременно попадают в эти интервалы.
– число пар отсчётов, которые одновременно попадают в эти интервалы.
Для этого разбивают диапазон изменения переменных 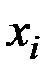 и
и 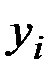 на разряды (интервалы) равной ширины, образующие в совокупности таблицу с двумя входами.
на разряды (интервалы) равной ширины, образующие в совокупности таблицу с двумя входами.
Затем подсчитывают число точек, попадающих в каждую клетку таблицы, и это число делят на площадь клетки 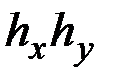 и объём выборки n.
и объём выборки n.
Случайное поле (случайный процесс с многомерным временем, или с многомерным параметром) – случайная функция, заданная на множестве точек какого–то многомерного пространства.
Примерами случайных полей, зависящих от трёх пространственных координат (а также и от времени), могут служить поля компонент скорости, давления и температуры турбулентного течения жидкости и газа. Шероховатость поверхности (высота взволнованности моря) – случайное поле с двумя координатами.
Теория случайных полей общего вида фактически не отличается от общей теории СФ. Более содержательные конкретные результаты удается получить лишь для ряда специальных классов полей, обладающих дополнительными свойствами, облегчающими их изучение.
Пример 7.1. Являются ли периодическими процессы:
X(t) = a1sin(2t + Q1) + a2sin(3t + Q2) + a3sin(7t + Q3);
Y(t) = a1sin(2t + Q1) + a2sin(3t + Q2) + a3sin( 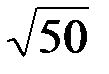 t + Q3) ?
t + Q3) ?
Решение. Сумма нескольких синусоид образует периодический процесс только в том случае, если отношения всех возможных пар частот представляет собой рациональные числа. Это означает, что существует некоторый основной период, удовлетворяющий формуле:
X(t) = X(t ± nT0), n = 1,2,3¼
Поэтому процесс X(t) периодический, поскольку 2/3, 2/7, 3/7 – рациональные числа (с основным периодом равным 1).
Процесс Y(t) не является периодическим, поскольку числа 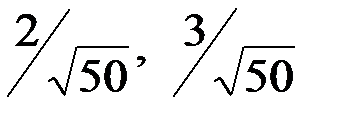 иррациональные (и основной период равен бесконечности).
иррациональные (и основной период равен бесконечности).
Процесс Y(t) является почти периодическим, но соотношение, записанное для X(t) не удовлетворяется при любых конечных значениях T0.
Пример 7.2. Периодический процесс формируется в результате сложения трёх синусоидальных волн с частотами 60, 75, 100 Гц. Определить основной период этого процесса. Как будет выглядеть ряд Фурье этого процесса?
Решение. Наибольший общий делитель указанных частот равен пяти, поэтому период результирующего периодического процесса составляет 0,2 секунд. Следовательно, при разложении в ряд Фурье значения cn будут равны нулю при всех n, кроме n = 12, n = 15, n = 20.
Пример 7.3. Элементарная случайная функция имеет вид 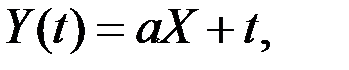 где X – случайная величина с характеристиками m и s; a – неслучайная величина. Требуется найти характеристики Y(t).
где X – случайная величина с характеристиками m и s; a – неслучайная величина. Требуется найти характеристики Y(t).
Решение. Все характеристики выразим по их определению.
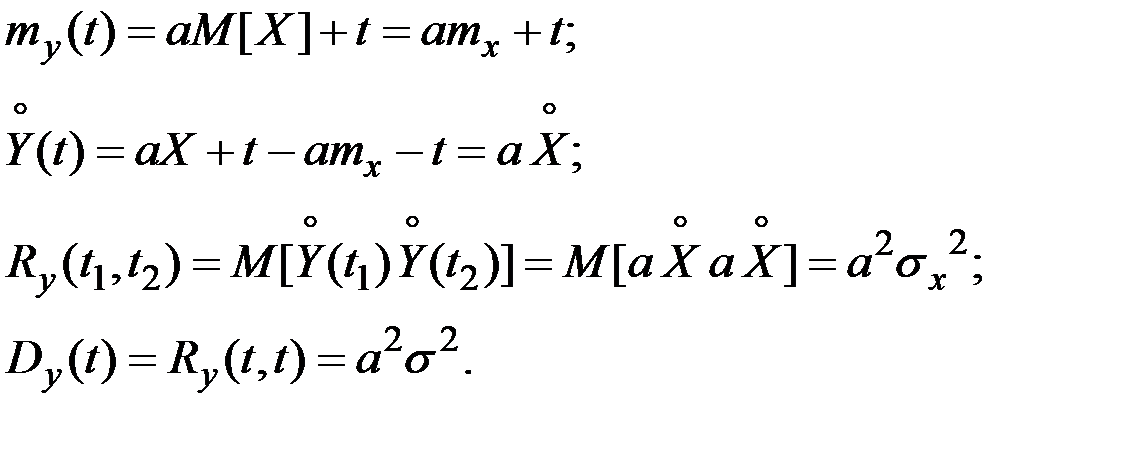
Пример 7.4. Случайная функция имеет вид 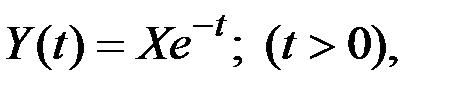 где X – случайная величина, распределенная по нормальному закону с параметрами m и s. Требуется найти основные характеристики функции Y(t).
где X – случайная величина, распределенная по нормальному закону с параметрами m и s. Требуется найти основные характеристики функции Y(t).
Решение. Математическое ожидание и дисперсию функции Y(t) выразим по их определению:
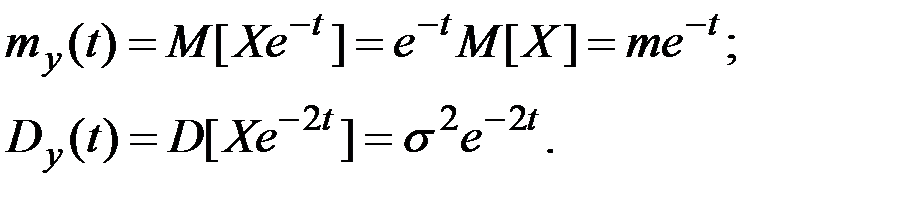
Найдём корреляционную функцию. Центрируем функцию Y(t):
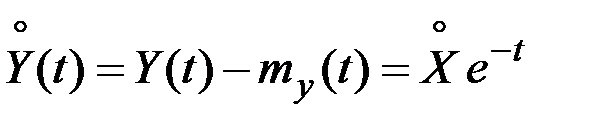 .
.
Тогда 
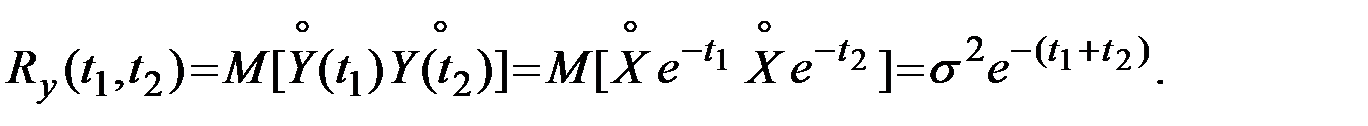
Пример 7.5. Мощность угольного пласта с математическим ожиданием (средним значением) 3,4 метра является нормальной стационарной случайной функцией по направлению отработки с автокорреляционной функцией 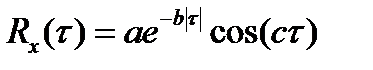 (τ – в метрах). Скорость продвижения забоя V равна 1,5 м/ч. В текущий момент обработки пласта его мощность равна 4,0 метра. Определить вероятность того, что через 2 часа работы мощность пласта будет больше 4,4 метра, если параметры АКФ следующие: a = 2 м2; b = 0,1 м2; с = 0,2 м–1.
(τ – в метрах). Скорость продвижения забоя V равна 1,5 м/ч. В текущий момент обработки пласта его мощность равна 4,0 метра. Определить вероятность того, что через 2 часа работы мощность пласта будет больше 4,4 метра, если параметры АКФ следующие: a = 2 м2; b = 0,1 м2; с = 0,2 м–1.
Решение. Обозначим x1 = X(t1) = 4 м; x2 = X(t1 + 2).
Для условного закона распределения x 2 имеем
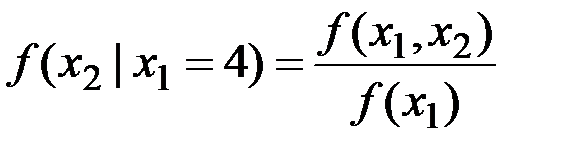 ,
,
где f(x1,x2) – нормальный закон распределения системы СВ с корреляционной матрицей 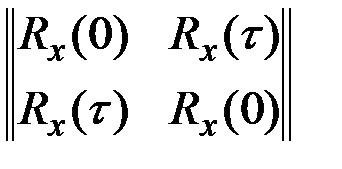 , t = (2 часа)×(1,5 м/час) = 3 метра.
, t = (2 часа)×(1,5 м/час) = 3 метра.
Если рассмотреть 2 СВ x = X(t1) = 4 м; y = X(t1 + 2), то для величины y имеем условный закон распределения из системы двух нормальных СВ:
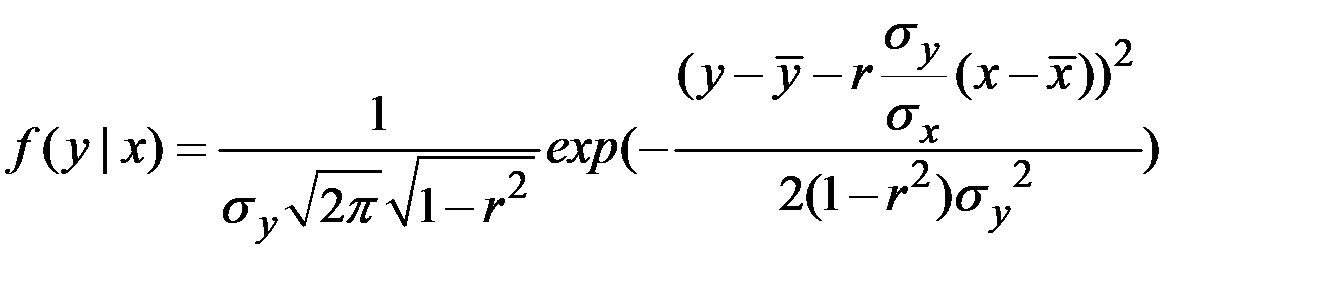 .
.
Искомая вероятность определиться следующим образом:
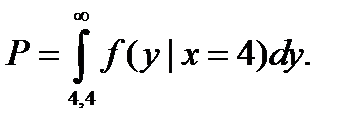
Вычислим неизвестные параметры этой формулы.
Имеем для эргодического процесса:
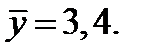
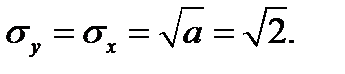
Расстояние между сечениями процесса в метрах равно:
t = (2 часа)×(1,5 м/час) = 3 м.
Коэффициент корреляции значений мощности пласта в двух сечениях составит величину
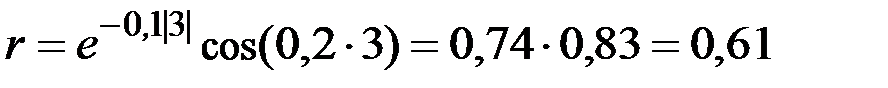 .
.
Условное среднее квадратическое значение мощности пласта через 3 метра 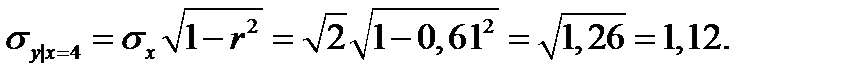
Условное среднее значений мощности пласта через 3 метра
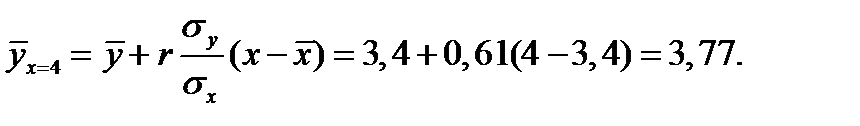
Тогда
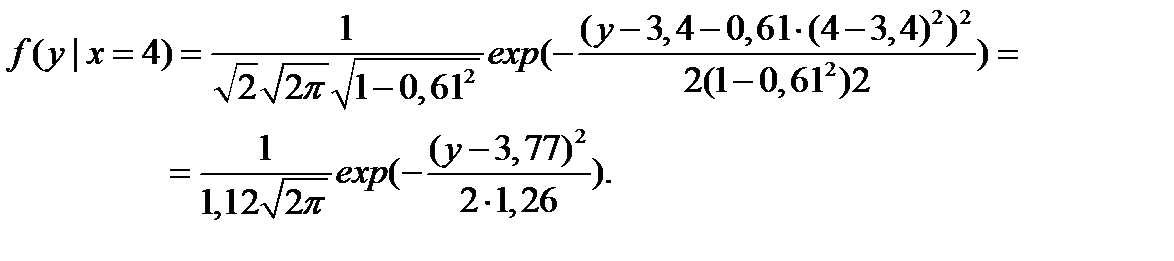
Используя таблицу функции распределения нормального закона (функцию Лапласа) определяем искомую вероятность
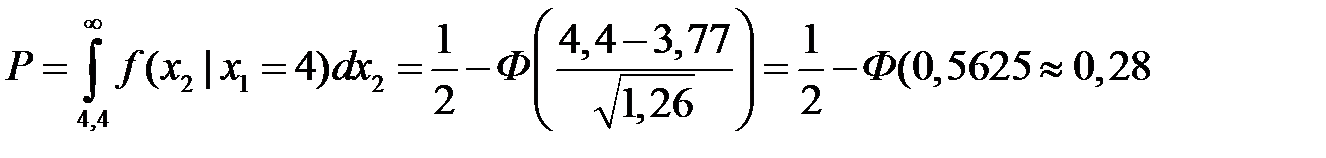 .
.
7.4. Преобразования случайных процессов
7.4.1. Дифференцирование случайных процессов
Случайный процесс X(t) будет дифференцируем в точке t, если для любой сходящейся к нулю последовательности чисел 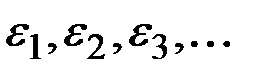 последовательность величин
последовательность величин 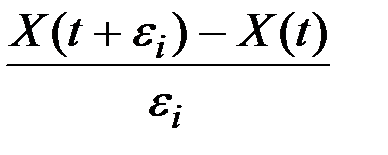 сходится к одной и той же СВ, которую называют производной процесса X(t) в точке t и обозначают
сходится к одной и той же СВ, которую называют производной процесса X(t) в точке t и обозначают 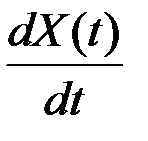 или
или 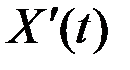 .
.
Для того, чтобы СФ X(t) имела производную, достаточно существование второй смешанной производной от корреляционной функции при равных значениях её аргументов.
Для стационарных СФ 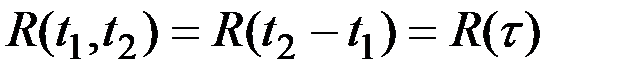 и, следовательно,
и, следовательно,
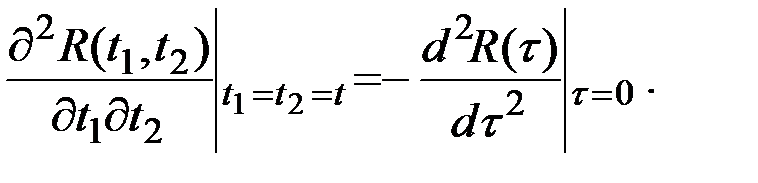
Для того, чтобы стационарная СФ была дифференцируема, достаточно существование второй частной производной от корреляционной функции 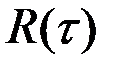 при нулевом значении её аргумента.
при нулевом значении её аргумента.
Пример 7.6. Четыре случайных процесса соответственно характеризуются следующими корреляционными функциями:
1. 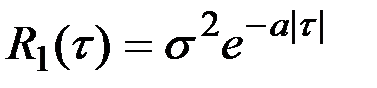 ; 3.
; 3. 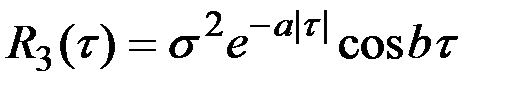 ;
;
2. 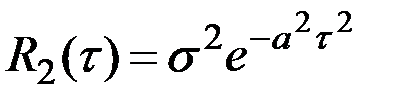 ; 4.
; 4. 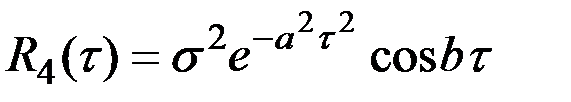 .
.
Являются ли эти процессы дифференцируемыми?
Решение. Вследствие наличия знака абсолютного значения у τ, при  первые производные от
первые производные от  и
и 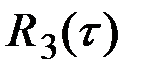 терпят разрыв, меняясь скачком на
терпят разрыв, меняясь скачком на 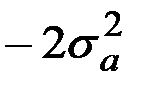 , и, следовательно, вторая производная не существует (рис.7.8).
, и, следовательно, вторая производная не существует (рис.7.8).
Наоборот, первые производные от функций 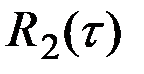 и
и 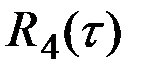 остаются непрерывными и дифференцируемыми при любых значениях τ и, следовательно, корреляционные функции подобного вида соответствуют дифференцируемым случайным процессам
остаются непрерывными и дифференцируемыми при любых значениях τ и, следовательно, корреляционные функции подобного вида соответствуют дифференцируемым случайным процессам
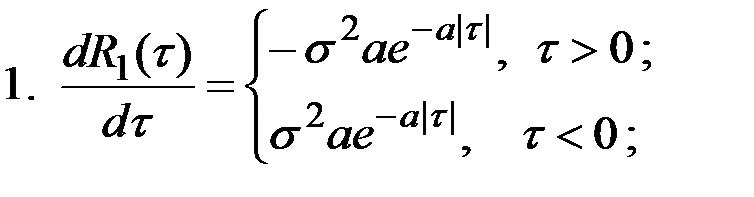
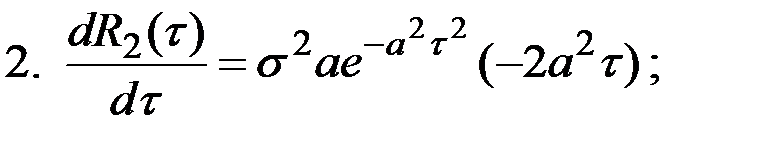
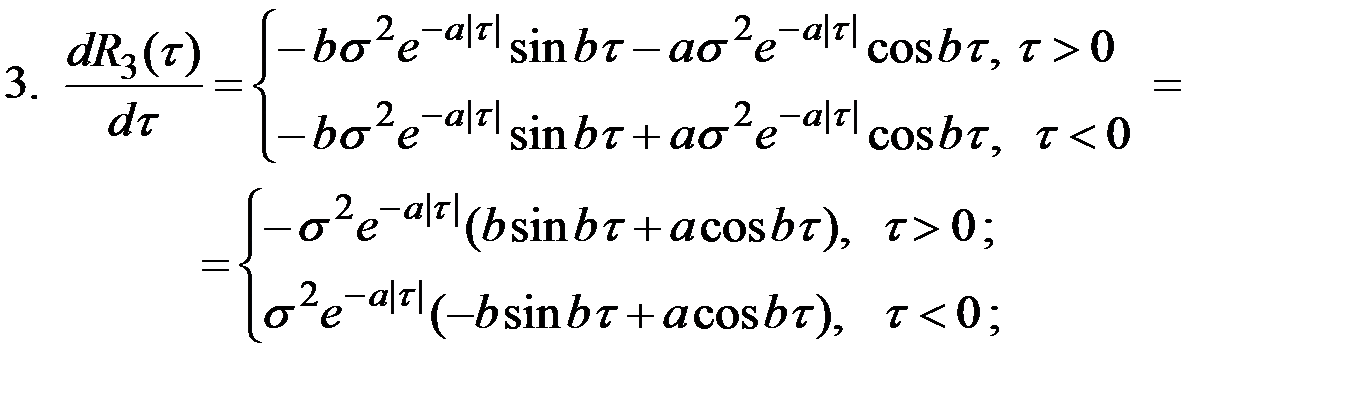
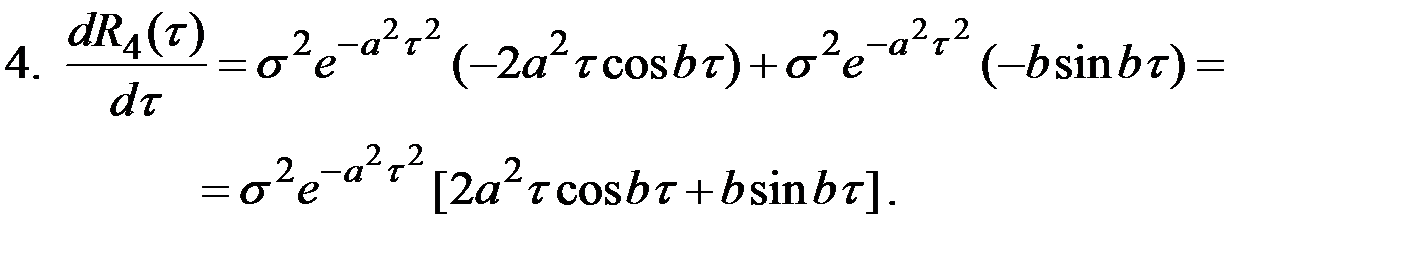
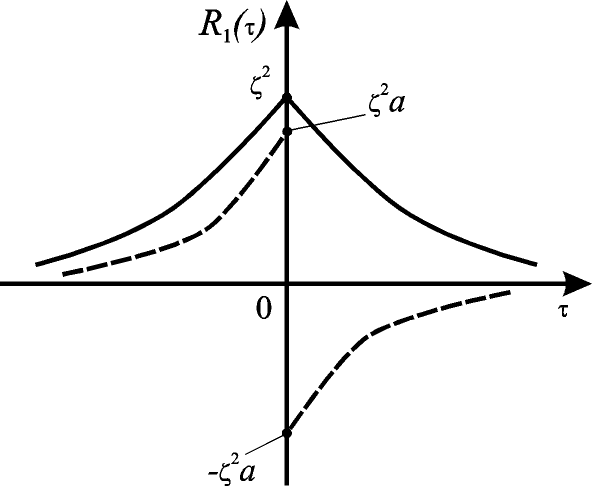
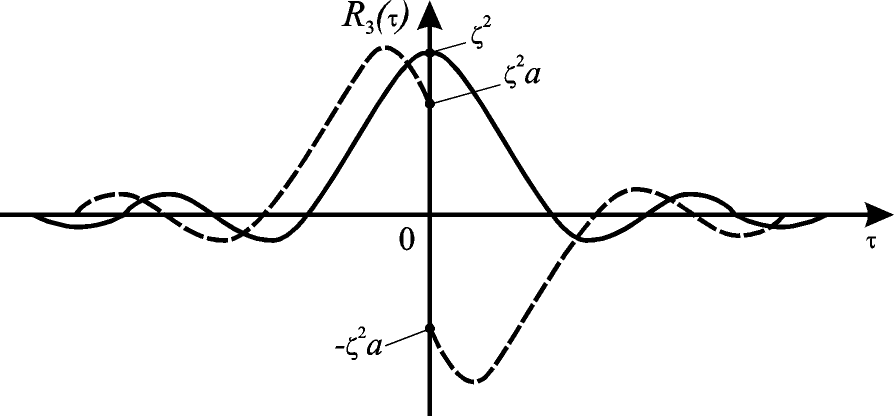
Рис.7.8. Графики корреляционных функций некоторых процессов
АКФ 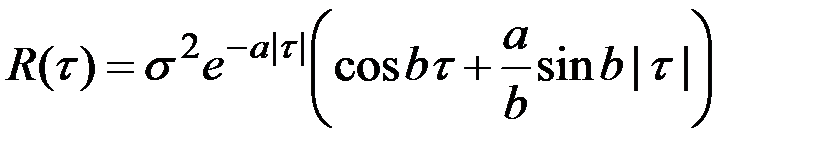 также описывает дифференцируемый процесс, так как производная
также описывает дифференцируемый процесс, так как производная 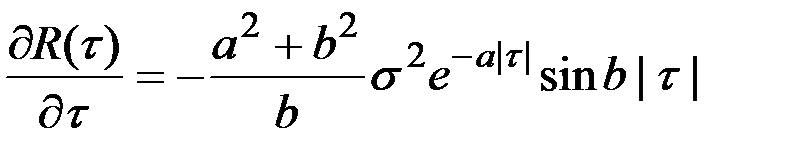 в нуле непрерывна и дифференцируема.
в нуле непрерывна и дифференцируема.
Дифференцируемому процессу также соответствует корреляционная функция 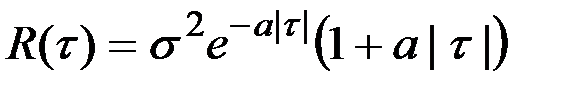 .
.
Непрерывные СФ, не имеющие производных, довольно часто встречаются в приложениях. Подобные функции возникают, например, в тех случаях, когда ордината случайной функции получается в результате суммирования бесконечно большого числа бесконечно малых взаимно независимых приращений.
Пусть СФ 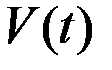 является производной СФ
является производной СФ 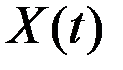 :
:
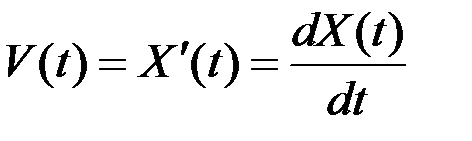 .
.
Тогда АКФ производной равна второй смешанной частной производной от корреляционной функции дифференцируемого процесса:
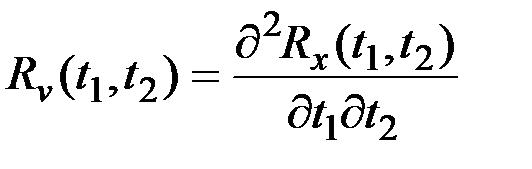 ,
,
Если функция Х(t) дифференцируема, то её производная в свою очередь является СФ времени, имеющей свои многомерные законы распределения и свою корреляционную функцию.
Законы распределения ординат производной от СФ легко определяются только в некоторых случаях, тогда как АКФ производной легко выражается через АКФ процесса.
Если функция Х(t) стационарна, т.е. справедливы соотношения 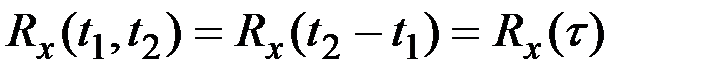 ;
;
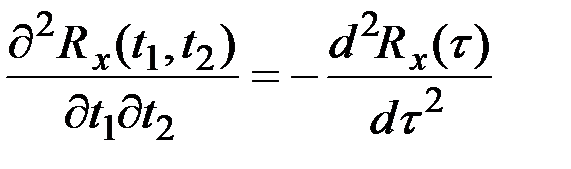 ,
,
то получим для производной: 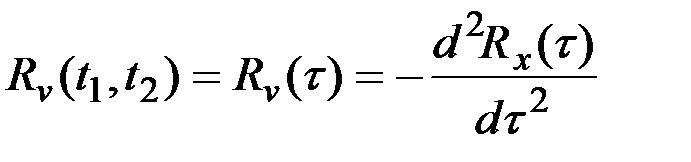 ,
,
т.е. корреляционная функция производной зависит только от τ.
Следовательно, производная от стационарной СФ является также стационарной СФ.
7.4.2. Интегрирование случайных процессов
Интеграл 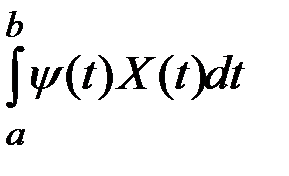 (где
(где 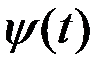 – неслучайная функция; a, b – постоянные величины) понимается как предел соответствующей интегральной суммы:
– неслучайная функция; a, b – постоянные величины) понимается как предел соответствующей интегральной суммы:
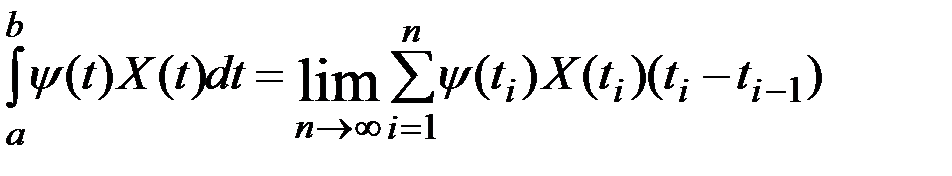 ,
,
где при 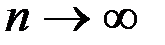 длина каждого интервала
длина каждого интервала 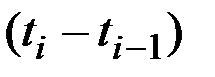 стремится к нулю, а предел понимается в смысле среднего квадратического.
стремится к нулю, а предел понимается в смысле среднего квадратического.
Для существования интеграла от СФ указанного вида должен существовать интеграл от соответствующей корреляционной функции вида
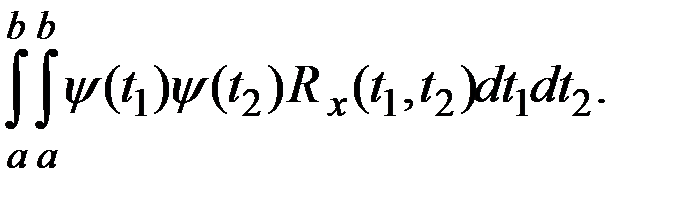 .
.
Пусть в частном случае 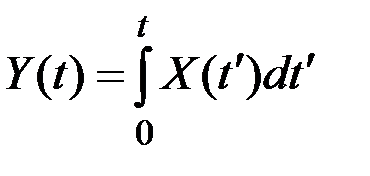 .
.
Здесь 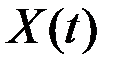 – случайный процесс, корреляционная функция которого предполагается известной, а его математическое ожидание без нарушения общности будем считать равным нулю.
– случайный процесс, корреляционная функция которого предполагается известной, а его математическое ожидание без нарушения общности будем считать равным нулю.
Для существования этого интеграла в определённой области изменения верхнего предела 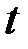 должен существовать в той же области двойной интеграл
должен существовать в той же области двойной интеграл 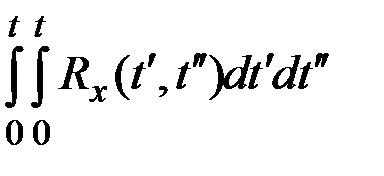 .
.
Предположим, что это условие выполнено и определим корреляционную функцию 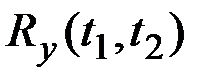 . Имеем:
. Имеем:
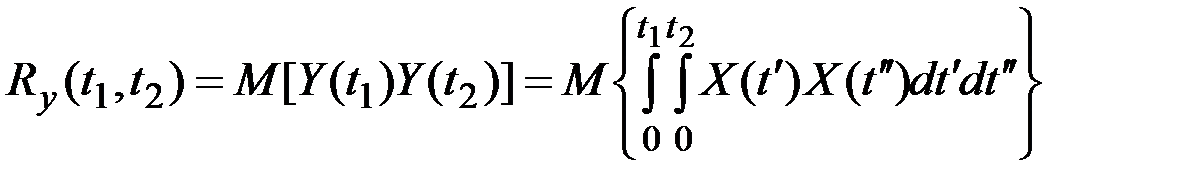 .
.
Меняя местами операцию интегрирования и операцию нахождения математического ожидания, получим:
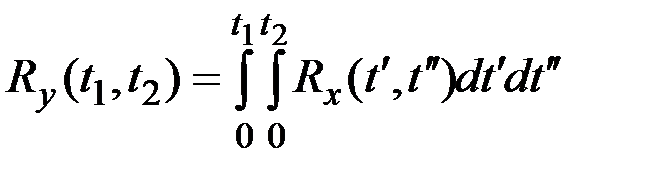 .
.
Для стационарной СФ будем иметь
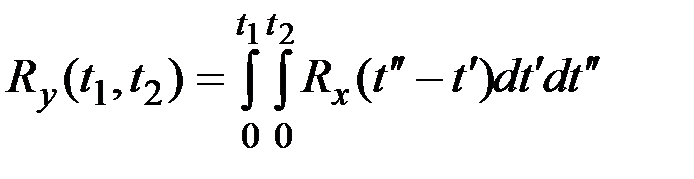 .
.
Выражение, стоящее справа, зависит в отдельности от 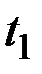 и
и 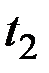 , а не от их разности, и, следовательно, интеграл от стационарной функции не обладает свойством стационарности. Однако, вследствие стационарности
, а не от их разности, и, следовательно, интеграл от стационарной функции не обладает свойством стационарности. Однако, вследствие стационарности 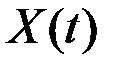 последнюю формулу можно упростить:
последнюю формулу можно упростить:
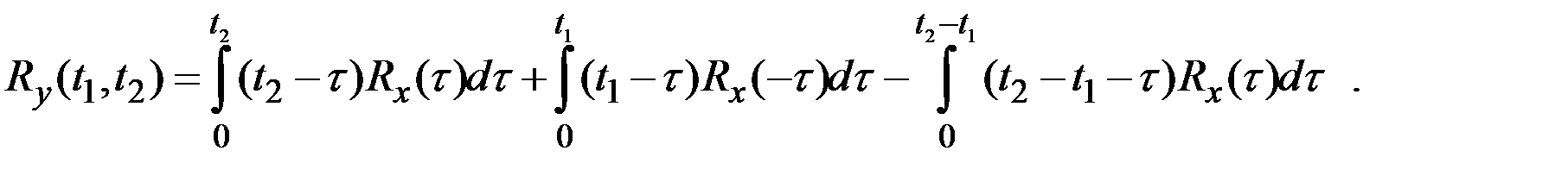
При 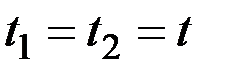 , для дисперсии интеграла
, для дисперсии интеграла 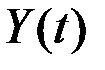 получим выражение, явно зависящее от t. Это означает, что в общем случае интеграл от стационарной СФ свойством стационарности не обладает:
получим выражение, явно зависящее от t. Это означает, что в общем случае интеграл от стационарной СФ свойством стационарности не обладает:
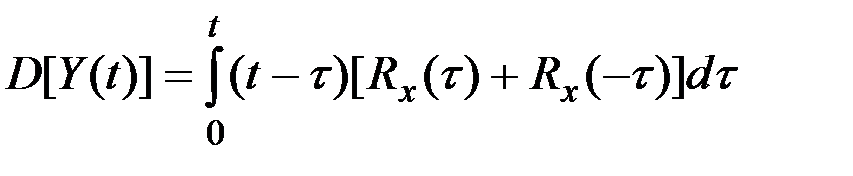 .
.
Тогда для вещественной случайной функции можно записать
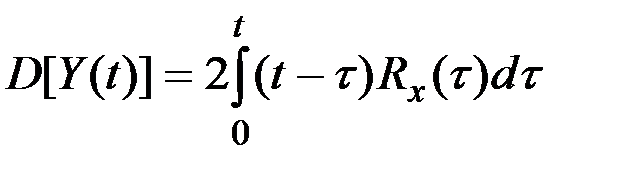 .
.
При выводе формул для корреляционной функции производной и интеграла от случайного процесса мы считали, что математическое ожидание 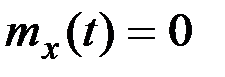 . Если бы это условие не выполнялось, то формулы для корреляционной функции остались бы без изменения, значение
. Если бы это условие не выполнялось, то формулы для корреляционной функции остались бы без изменения, значение 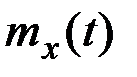 нужно было бы учесть только при вычислении математического ожидания производной и интеграла.
нужно было бы учесть только при вычислении математического ожидания производной и интеграла.
В случае дифференцирования, находя математическое ожидание от обеих частей равенства 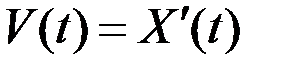 , и учитывая, что операцию нахождения математического ожидания и операцию дифференцирования можно лишь менять местами, получим
, и учитывая, что операцию нахождения математического ожидания и операцию дифференцирования можно лишь менять местами, получим
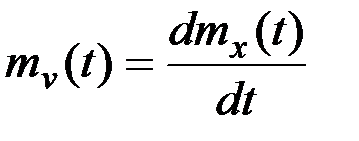 .
.
Для интегрирования случайного процесса, применяя операцию нахождения математического ожидания к обеим частям равенства
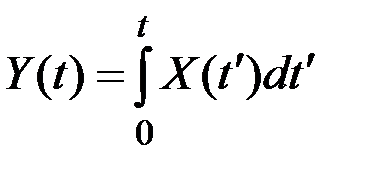 ,
,
получим 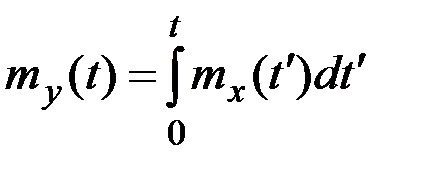 .
.
Все результаты этого раздела применимы как к нормальным случайным процессам, так и к процессам, не являющимся нормальными.
Однако у нормальных процессов имеется одна особенность, существенно облегчающая использование полученных соотношений.
Известно, что сумма любого числа слагаемых, образующих систему нормальных СВ, даёт нормальную СВ. Поэтому можно утверждать, что как производная, так и интеграл от нормального случайного процесса являются также нормальными процессами, которые полностью могут быть охарактеризованы их математическими ожиданиями и корреляционными функциями.
Следовательно, формулы для нормального процесса позволяют характеризовать его производную и интеграл не только в рамках корреляционной теории, но дают исчерпывающую характеристику этих процессов.
7.4.3. Линейные преобразования случайных процессов
Если случайную функцию 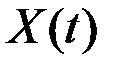 подвергают некоторому преобразованию
подвергают некоторому преобразованию 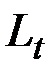 , то получается другая СФ
, то получается другая СФ
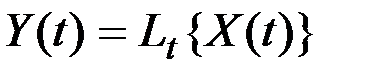 .
.
Преобразование 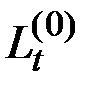 (оператор) называется линейным однородным, если выполняются условия аддитивности и однородности:
(оператор) называется линейным однородным, если выполняются условия аддитивности и однородности:
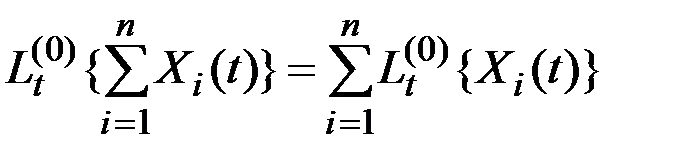 ;
;
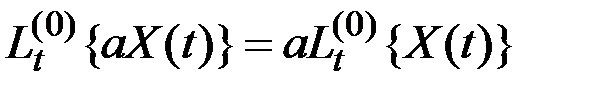 , где
, где  .
.
Примеры линейных однородных операторов:
1) оператор дифференцирования: 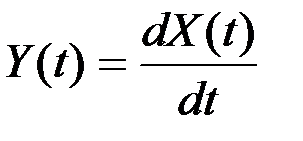 ;
;
2) оператор интегрирования: 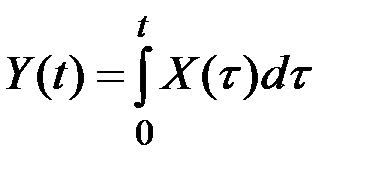 ;
;
3) оператор умножения на определенную функцию 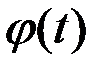 :
:
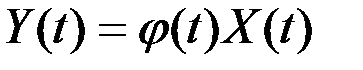 ;
;
4) оператор интегрирования с заданным весом 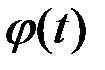 :
:
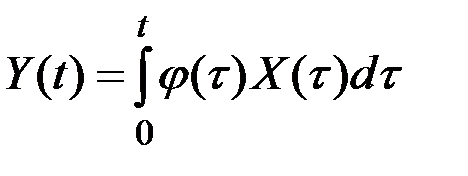 .
.
Преобразование 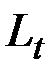 называется линейным неоднородным, если
называется линейным неоднородным, если
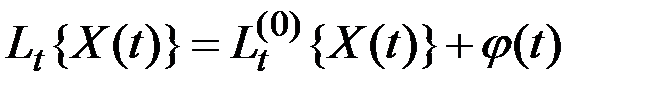 ,
,
где 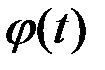 – любая функция, никак не связанная с
– любая функция, никак не связанная с 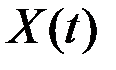 .
.
Однородная компонента 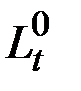 однозначно определена по
однозначно определена по 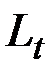 .
.
Примеры линейных неоднородных операторов:
1) 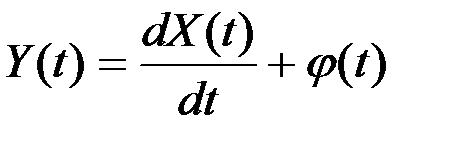 ;
;
2) 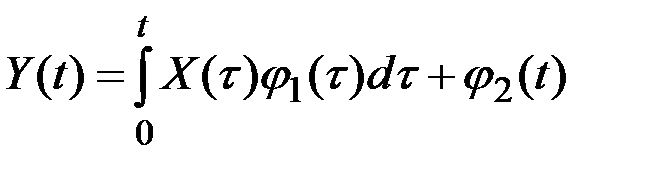 ;
;
3) 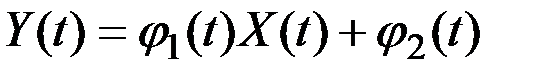 .
.
Если СФ 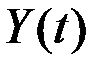 связана со СФ
связана со СФ 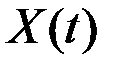 линейным преобразованием
линейным преобразованием
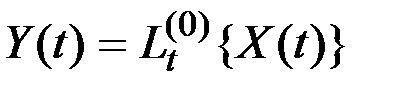 ,
,
то её математическое ожидание 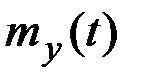 получается из
получается из 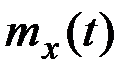 тем же линейным преобразованием
тем же линейным преобразованием
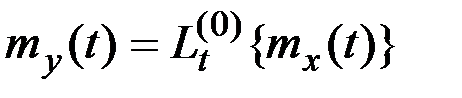 ,
,
а для нахождения  нужно дважды подвергнуть функцию
нужно дважды подвергнуть функцию 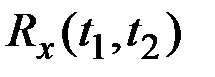 , соответствующему линейному однородному преобразованию, один раз по
, соответствующему линейному однородному преобразованию, один раз по 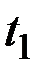 , другой раз по
, другой раз по 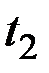 :
:
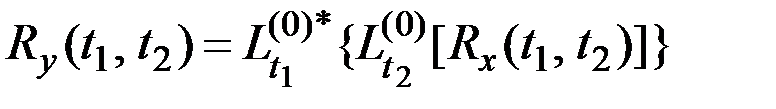 ,
,
где 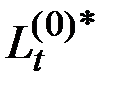 – оператор, полученный из
– оператор, полученный из 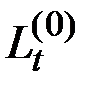 путём замены всех коэффициентов на комплексно–сопряжённые (для конечномерных операторов).
путём замены всех коэффициентов на комплексно–сопряжённые (для конечномерных операторов).
При воздействии линейного неоднородного оператора
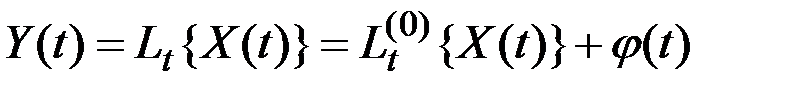
характеристики процесса 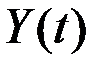 определяются следующим образом:
определяются следующим образом:
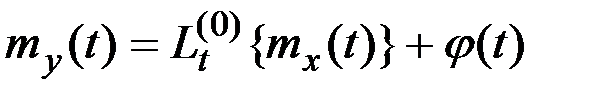 ;
;
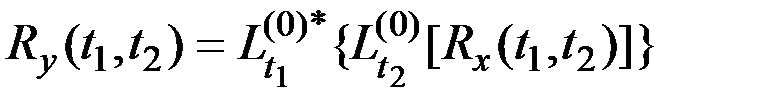 .
.
Возможность применения оператора к процессу должна быть проверена в каждом конкретном случае.
Случайный процесс дифференцируем (один раз), если его корреляционная функция имеет вторую смешанную частную производную при равных значениях её аргументов, что для стационарных СФ эквивалентно существованию второй производной от 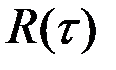 при
при 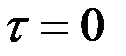 .
.
При прибавлении к СФ неслучайного слагаемого 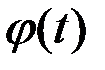 к её математическому ожиданию прибавляется то же неслучайное слагаемое, а корреляционная функция не изменяется.
к её математическому ожиданию прибавляется то же неслучайное слагаемое, а корреляционная функция не изменяется.
При умножении СФ 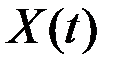 на неслучайный множитель
на неслучайный множитель 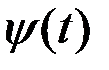 её математическое ожидание умножается на тот же множитель
её математическое ожидание умножается на тот же множитель 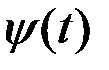 , а корреляционная функция на
, а корреляционная функция на 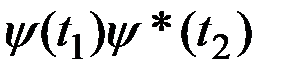 , т.е. если
, т.е. если
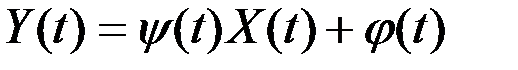 ,
,
то 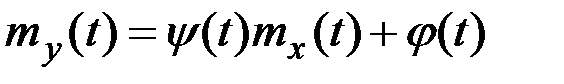 ,
,
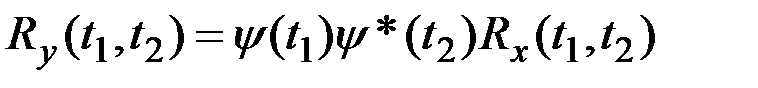 ,
,
где 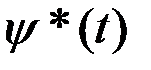 получается из
получается из 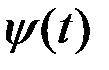 заменой всех коэффициентов на комплексно–сопряжённые.
заменой всех коэффициентов на комплексно–сопряжённые.
Если 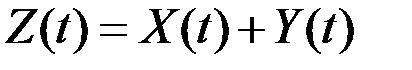 ,
,
то
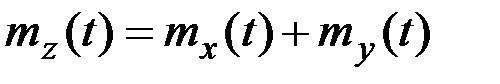 ;
;
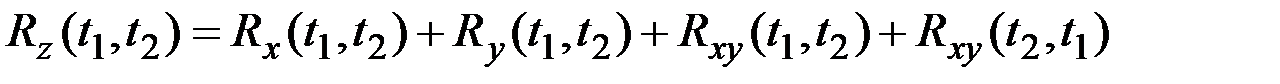 .
.
В общем случае, если 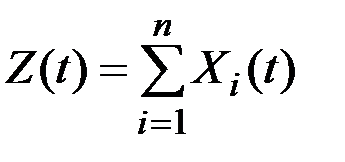 , то
, то
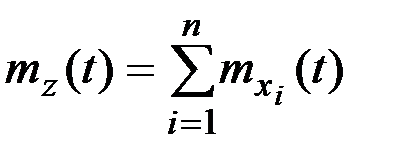 ;
;
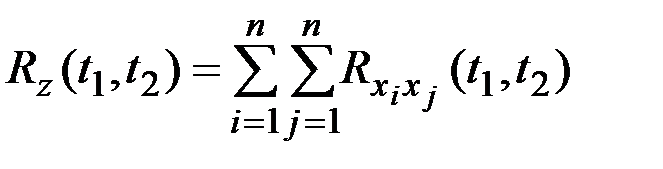 .
.
Линейное преобразование нормального стационарного процесса даёт также нормальный (не обязательно стационарный из–за неслучайного множителя) процесс.
Встречаются также и нелинейные операторы, нелинейные преобразования процессов, например:
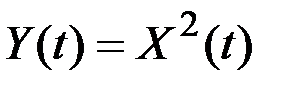 ;
; 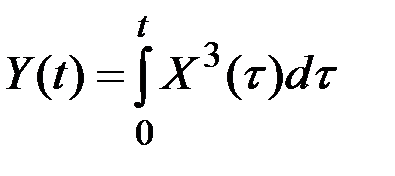 ;
; 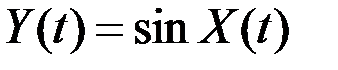 .
.
Методы исследования нелинейных систем значительно сложнее линейных. Однако многие реальные системы в известных пределах допускают линеаризацию. Если случайные возмущения на входе системы достаточно малы, то практически любая система может рассматриваться (в пределах этих малых возмущений) как приближённо линейная, подобно тому как при достаточно малых случайных изменениях аргументов практически любая функция может быть линеаризована.
Пример 7.7. На вход дифференцирующего механизма поступает случайный сигнал 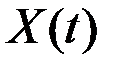 с математическим ожиданием
с математическим ожиданием 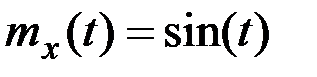 и корреляционной функцией
и корреляционной функцией 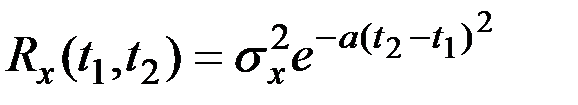 . Определить математическое ожидание и дисперсию сигнала на выходе системы.
. Определить математическое ожидание и дисперсию сигнала на выходе системы.
Решение. Случайная функция 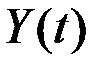 на выходе системы связана с
на выходе системы связана с 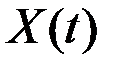 оператором дифференцирования
оператором дифференцирования
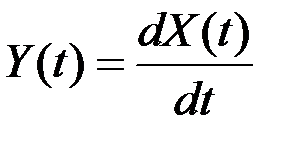 .
.
Применяя общие правила, имеем:
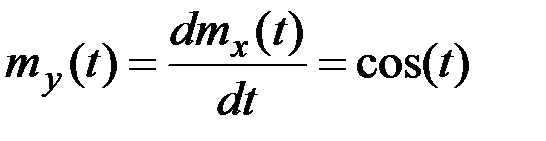 ;
;
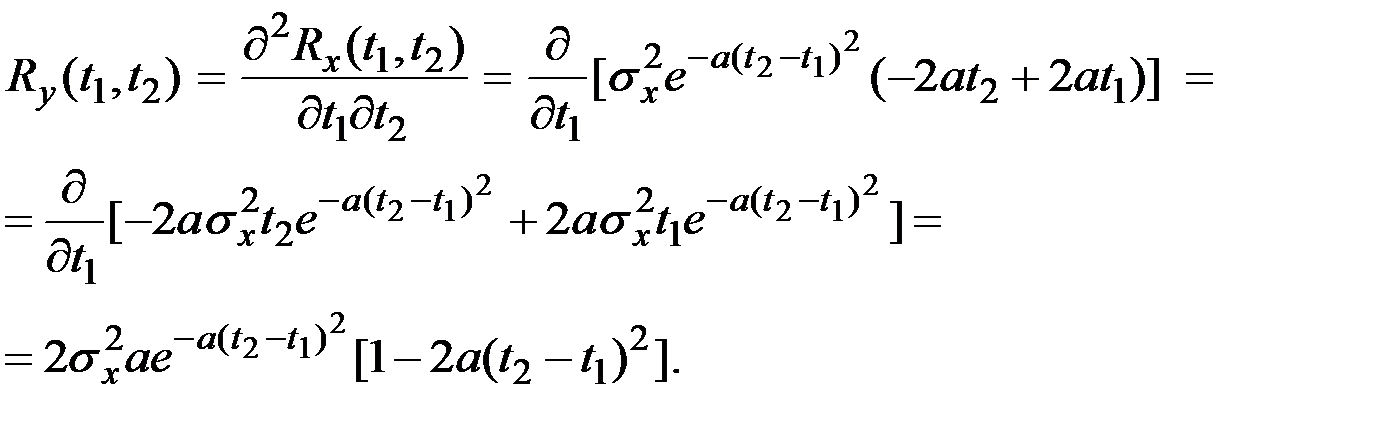
Полагая  , имеем
, имеем 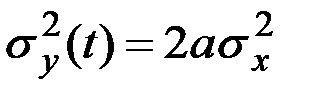 , т.е. дисперсия на выходе является постоянной величиной.
, т.е. дисперсия на выходе является постоянной величиной.
7.4.4. Каноническое представление случайных процессов
При линейных преобразованиях СФ её математическое ожидание подвергается тому же линейному преобразованию, а корреляционная функция подвергается этому линейному преобразований дважды.
Это правило часто приводит к громоздким вычислениям, что затрудняет практическое применение общих методов.
Например, для преобразования 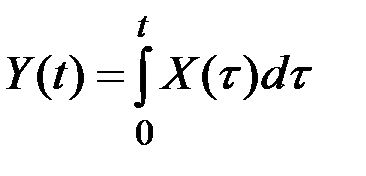 автокорреляционную функцию на выходе системы вычисляем по соотношению
автокорреляционную функцию на выходе системы вычисляем по соотношению
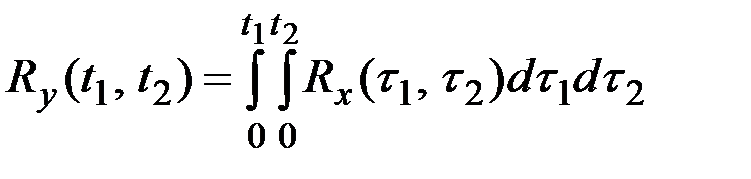 .
.
Часто бывает, что полученная из опыта АКФ не имеет аналитического выражения и задана таблицей, тогда двойной интеграл надо вычислять численно. Эта задача достаточно трудоёмкая. Если даже аппроксимировать подынтегральную функцию каким–либо выражением, то и в этом случае интеграл часто не выражается через известные функции.
В связи с этим на практике применение общих методов линейных преобразований СФ часто оказывается слишком сложным.
При решении практических задач чаще применяются другие методы, приводящие к более простым преобразованиям.
Один из них – метод канонических разложений.
Идея метода состоит в том, что СФ 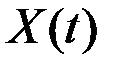 представляется в виде суммы элементарных СФ.
представляется в виде суммы элементарных СФ.
Функция называется элементарной, если она представлена в виде произведения случайной величины на неслучайную функцию:
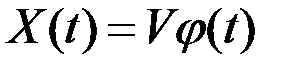 .
.
Например: 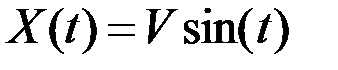 ;
; 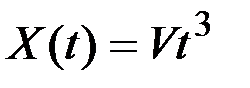 .
.
Вся случайность элементарной функции сосредоточена в коэффициенте, а зависимость от времени – в функции 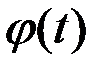 .
.
Пусть СФ представлена в виде разложения по элементарным СФ:
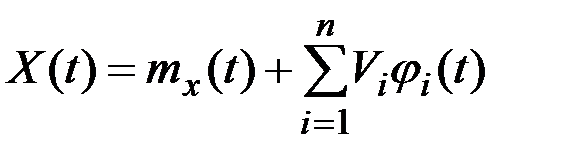 ,
,
где 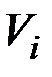 – коэффициенты разложения, т.е. центрированные СВ с дисперсиями
– коэффициенты разложения, т.е. центрированные СВ с дисперсиями 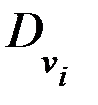 (
(  ; может быть и
; может быть и 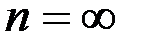 ) и
) и 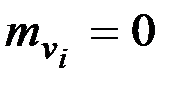 ;
;
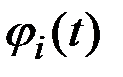 – неслучайные координатные функции.
– неслучайные координатные функции.
При линейном преобразовании случайной функции 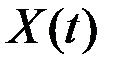 , заданной таким разложением, получается случайная функция
, заданной таким разложением, получается случайная функция 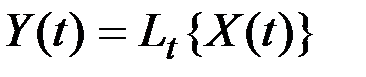 в виде разложения
в виде разложения
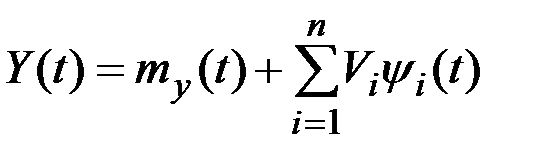 ,
,
где 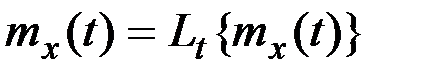 ;
;
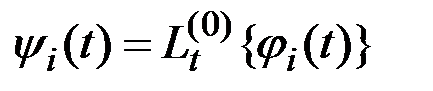 .
.
При линейном преобразовании СФ, заданной разложением по элементарным СФ, её математическое ожидание подвергается тому же линейному преобразованию, а координатные функции – соответствующему линейному однородному преобразованию.
Корреляционная функция процесса 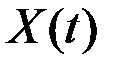 , заданного разложением по элементарным СФ, определяется соотношением
, заданного разложением по элементарным СФ, определяется соотношением
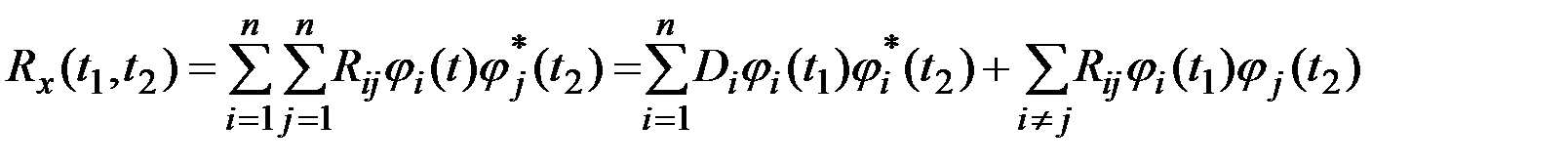 ,
,
где 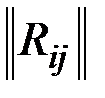 – корреляционная матрица системы величин
– корреляционная матрица системы величин 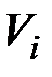 и
и 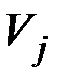 .
.
(корреляционные моменты между 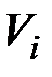 и
и 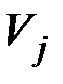 ).
).
Если величины 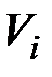 некоррелированы, т.е.
некоррелированы, т.е. 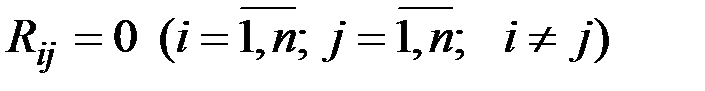 , то разложение называется каноническим.
, то разложение называется каноническим.
В этом случае
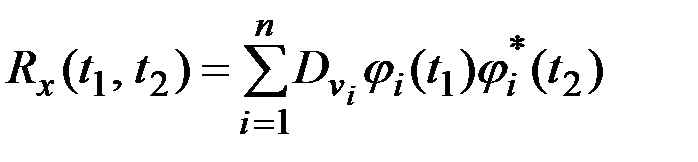
В частности, при 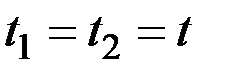 имеем
имеем
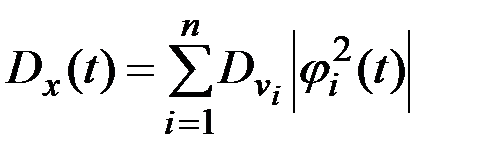 .
.
Таким образом, зная каноническое разложение СФ, можно найти каноническое разложение её корреляционной функции.
Справедливо и обратное.
Если дано каноническое разложение АКФ
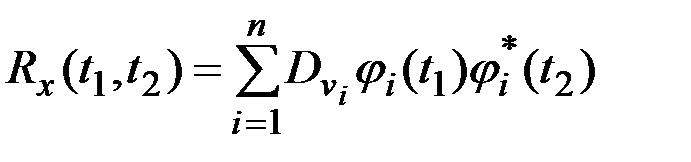 ,
,
то для 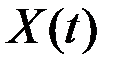 справедливо каноническое разложение
справедливо каноническое разложение
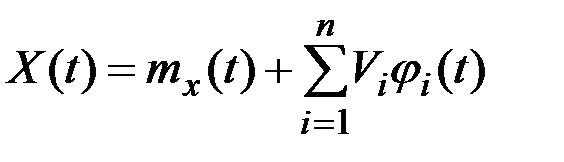 .
.
Если известны математическое ожидание 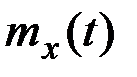 , дисперсия
, дисперсия 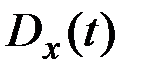 и корреляционная функция
и корреляционная функция 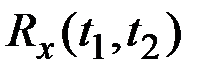 случайного процесса
случайного процесса 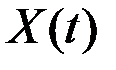 , то для определения дисперсии
, то для определения дисперсии 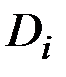 случайных величин
случайных величин 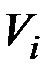 и координатных функций
и координатных функций 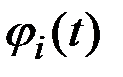 при представлении процесса в канонической форме используются следующие зависимости:
при представлении процесса в канонической форме используются следующие зависимости:
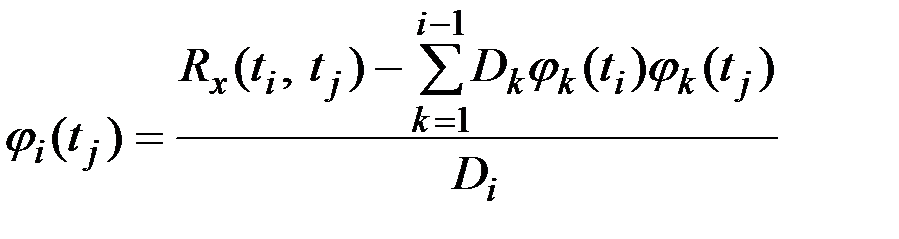 ;
;
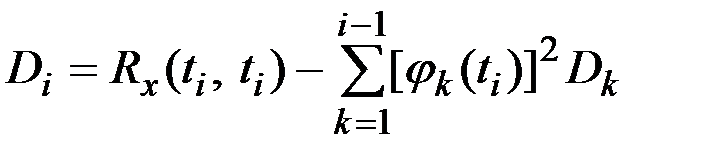 .
.
При этом следует иметь в виду, что при 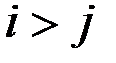
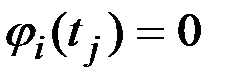 .
.
Пример 7.8. Представить в каноническом виде процесс, имеющий следующую корреляционную функцию в виде табл.7.2.
Таблица 7.2
Табличное представление автокореляционной функции
| tj ti | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,16 | 0,14 | 0,11 | 0,08 | 0,05 |
| 2 | 0,20 | 0,18 | 0,17 | 0,14 | |
| 3 | 0,23 | 0,20 | 0,19 | ||
| 4 | 0,26 | 0,22 | |||
| 5 | 0,28 |
Решение. Для определения дисперсии 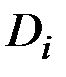 случайных величин
случайных величин 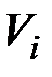 и координатных функций
и координатных функций 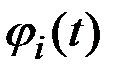 при представлении процесса в канонической форме используем приведенные выше зависимости.
при представлении процесса в канонической форме используем приведенные выше зависимости.
Получаем (рис.7.9):
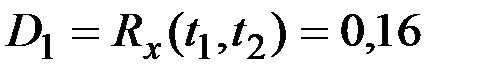 ;
;
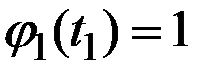 ;
;
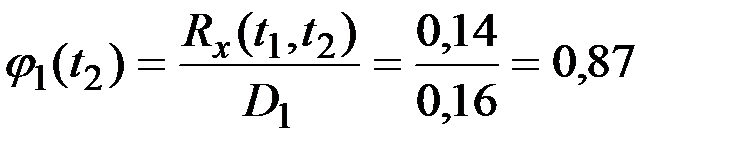 .
.
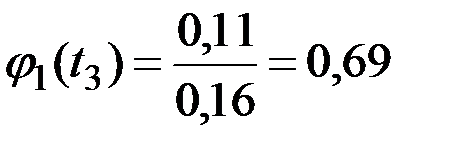 ;
;
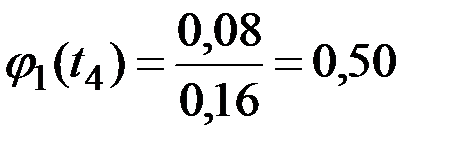 ;
;
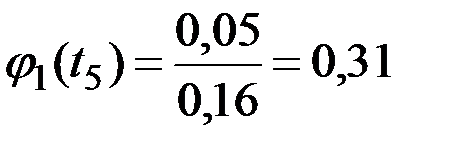 ;
;
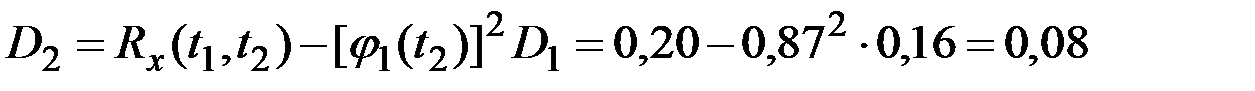 ;
;
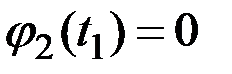 ;
;
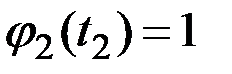 ;
;
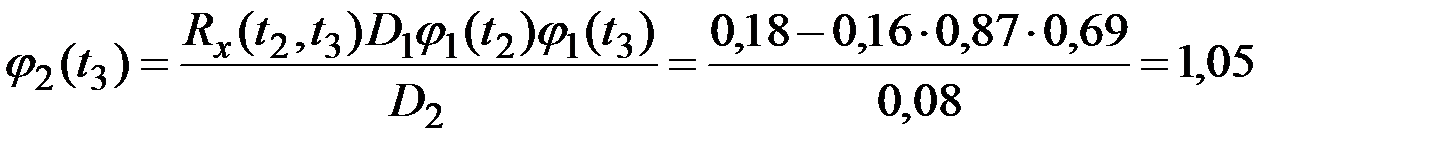 .
.
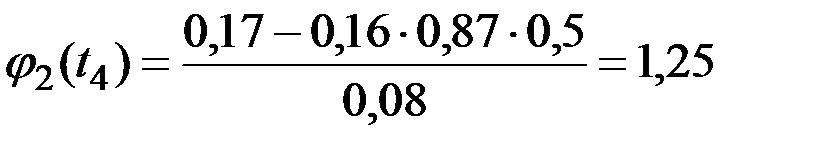 ;
;
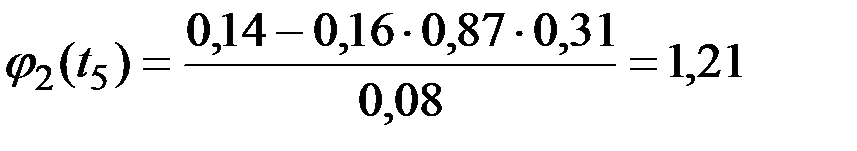 ;
;
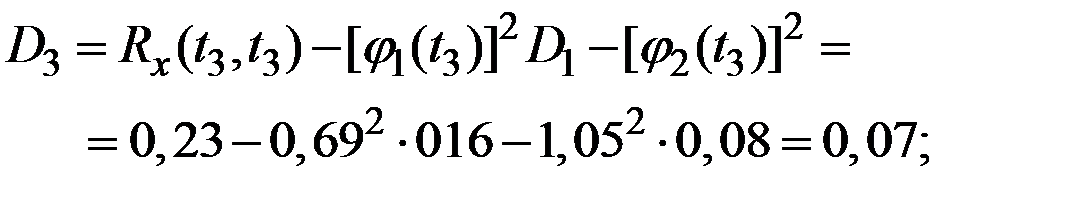
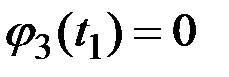 ;
;
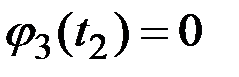 ;
;
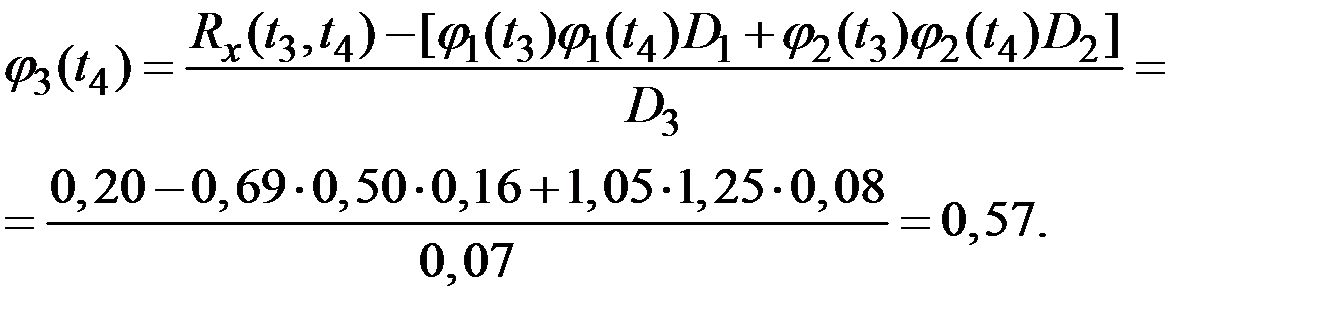
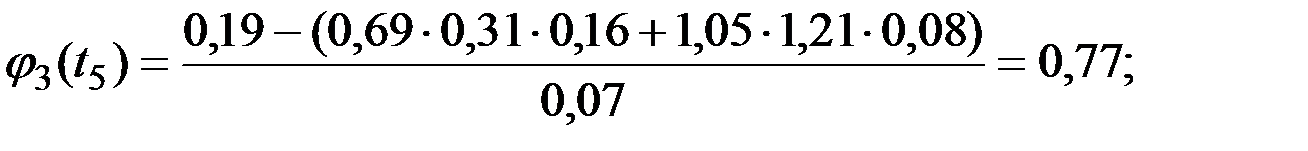
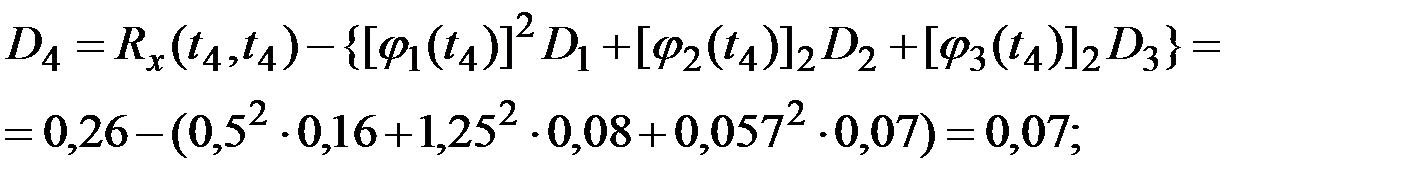
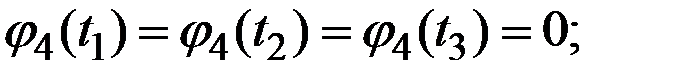
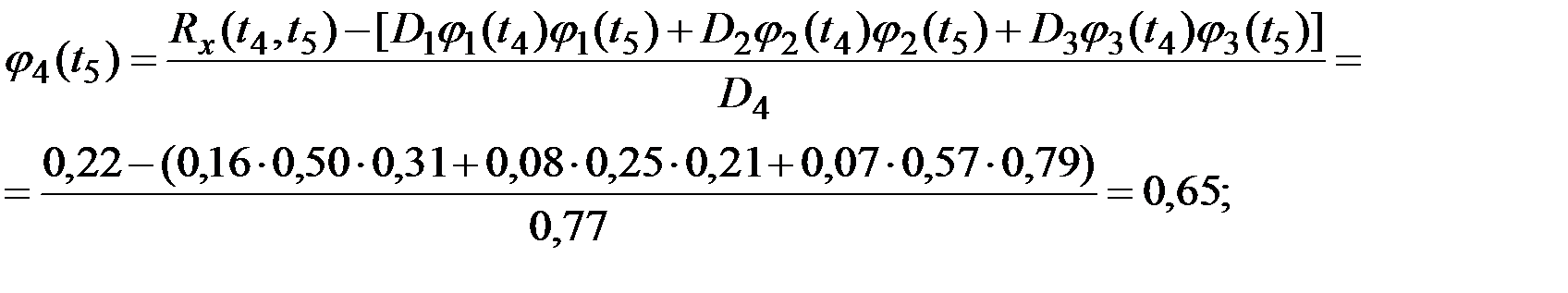
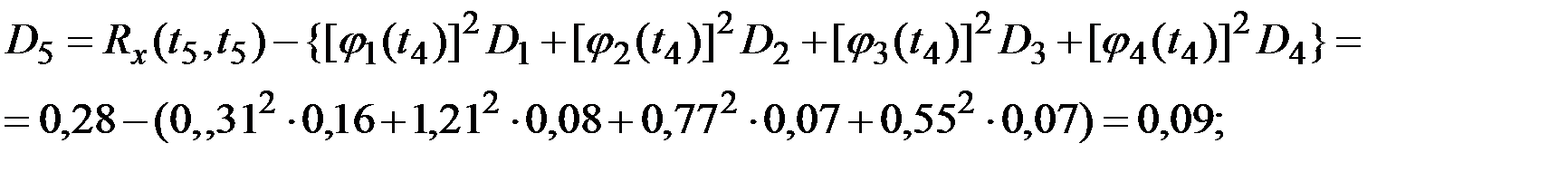
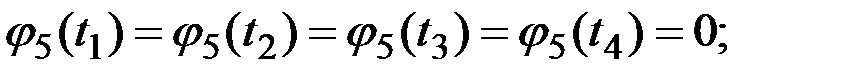
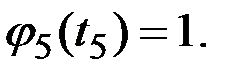

Рис.7.9. Координатные функции канонического разложения процесса
7.5. Выбросы случайных процессов
Выбросом случайной функции X(t) за данный уровень a называется событие [X(t) > a], т.е. пересечение снизу вверх графиком процесса горизонтальной прямой, отстоящей от оси t на расстояние a.
Вероятность того, что выброс произойдёт в бесконечно малом интервале времени dt, расположенном вблизи точки t, равна 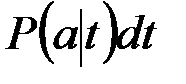 , где
, где
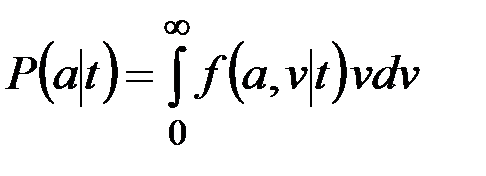 .
.
То есть, временная плотность вероятности 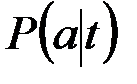 выражается через плотность вероятности
выражается через плотность вероятности 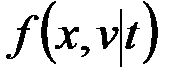 ординаты СФ X(t) и её производной
ординаты СФ X(t) и её производной 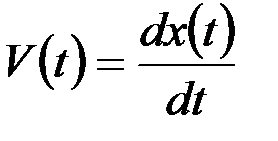 , вычисленной для момента времени t.
, вычисленной для момента времени t.
При малом среднем числе выбросов в течение интервала времени T вероятность 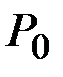 непоявления ни одного выброса за этот промежуток времени может быть приближенно оценена по формуле
непоявления ни одного выброса за этот промежуток времени может быть приближенно оценена по формуле 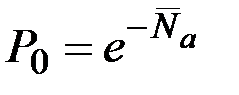 , т.е. число выбросов в данном интервале времени можно считать подчиняющимся закону Пуассона:
, т.е. число выбросов в данном интервале времени можно считать подчиняющимся закону Пуассона:
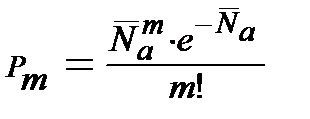 .
.
Для нормальных стационарных функций
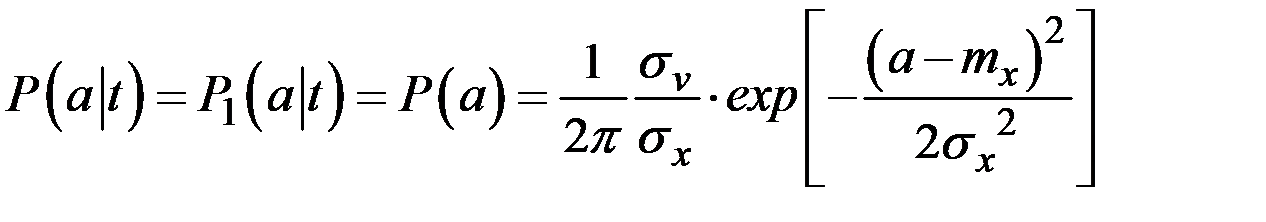 .
. 
Для стационарного процесса с одномерной плотностью f(x) и плотностью двумерного вектора 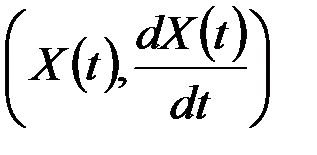 , равной f(x,v), среднее время
, равной f(x,v), среднее время 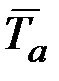 пребывания случайного процесса x(t) выше уровня в течение времени T, среднее число выбросов
пребывания случайного процесса x(t) выше уровня в течение времени T, среднее число выбросов 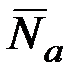 за этот же промежуток времени за уровень a и средняя длительность
за этот же промежуток времени за уровень a и средняя длительность 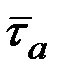 одного такого выброса определяются формулами
одного такого выброса определяются формулами
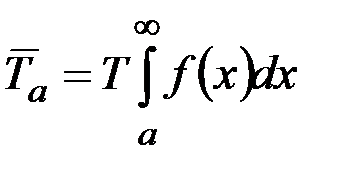 ;
;
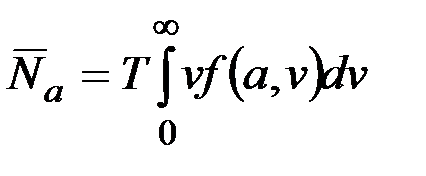 ;
;
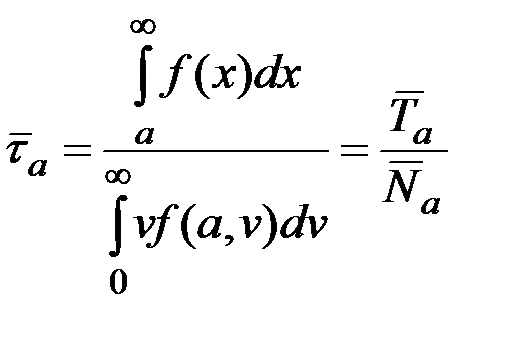 .
.
Среднее число выбросов стационарного процесса в единицу времени
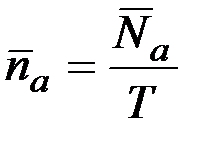 .
.
Для стационарного и нормального процесса эти формулы имеют вид
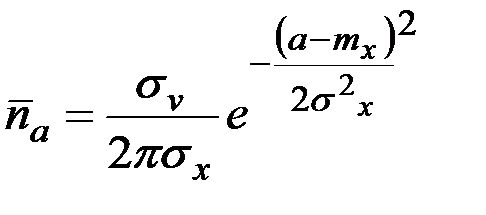 ;
;
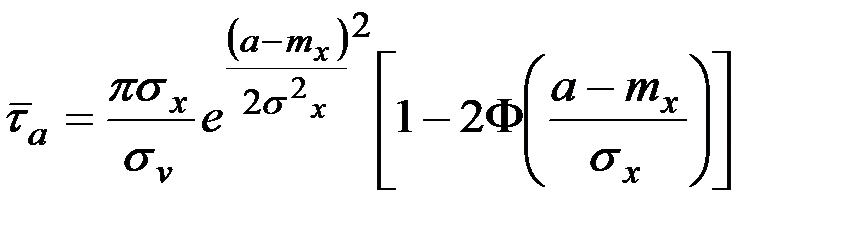 ;
;
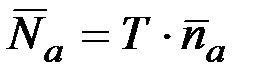 ;
; 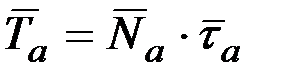 .
.








