Если функции меняются с изменением t, случайный процесс (фигурные скобки означают ансамбль, множество выборочных функций) называется нестационарным.
Если выполняются условия
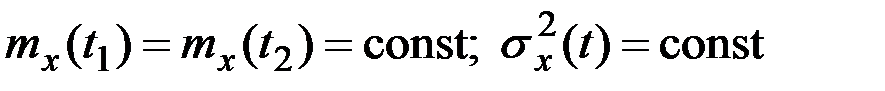(для всех 
);
,
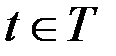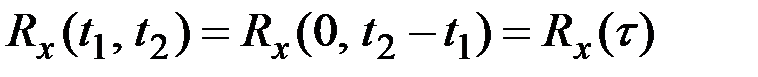то процесс будет слабо стационарным или стационарным в широком смысле, т.е. математическое ожидание и дисперсия стационарной СФ являются постоянными величинами, а корреляционная функция зависит от разности моментов времени, а не от самих моментов.
Когда все начальные и смешанные моменты распределений случайного процесса {X(t)} не зависят от времени (предполагается, что они существуют), случайный процесс называют стационарным или стационарным в узком смысле.
Случайный процесс стационарный в узком смысле, одновременно является стационарным и в широком смысле, но не наоборот.
Понятия стационарности в обоих смыслах совпадают только для гауссовских случайных процессов, плотности вероятностей в которых полностью определяются параметрами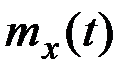 
и 
.
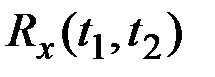Сумма двух нестационарных случайных процессов может оказаться стационарным случайным процессом.
Стационарный случайный процесс X(t) называется эргодическим, если его математическое ожидание и корреляционная функция одинаковы для различных выборочных функций.
Для эргодических стационарных функций одна реализация эквивалентна множеству реализаций.
Рассмотрим, например, две стационарные функции, представленных на рис.7.4.
а) б)
Рис.7.4. Два вида стационарных процессов
Каждая реализация СФ, изображенной на рис.7.4.а, обладает одними и теми же характерными признаками: средним значением, вокруг которого происходят колебания, и средним размахом этих колебаний.
Очевидно, что одна из таких произвольно выбранных реализаций при достаточно большом времени испытания сможет дать нам достаточно хорошее представление о свойствах СФ. В частности, усреднив значения этой реализации по времени, можно получить приближённое значение математического ожидания СФ.
Про СФ, каждая достаточно продолжительная реализация которой является как бы “полномочным представителем” всей совокупности возможных реализаций, говорят, что она обладает эргодическим свойством.
Если стационарная СФ X(t) обладает эргодическим свойством, то:
1) её математическое ожидание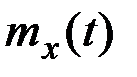 
приближённо равно средней по времени ординате одной произвольно взятой реализации x(t) достаточной продолжительности, т.е.
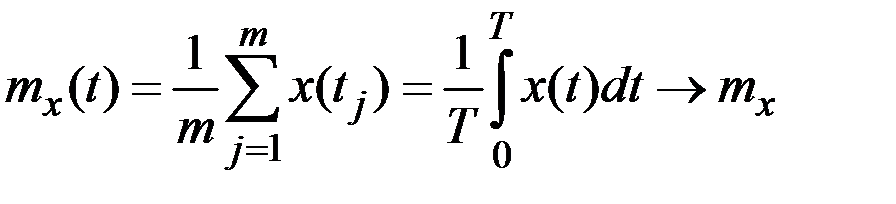при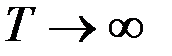 
;
2) значение корреляционной функции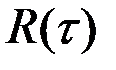 
при любом τ приближённо равно средней по времени произведений отклонений ординат реализации x(t) в точках, отстоящих друг от друга на величину τ, от математического ожидания стационарной СФ 
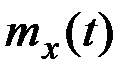, т.е.
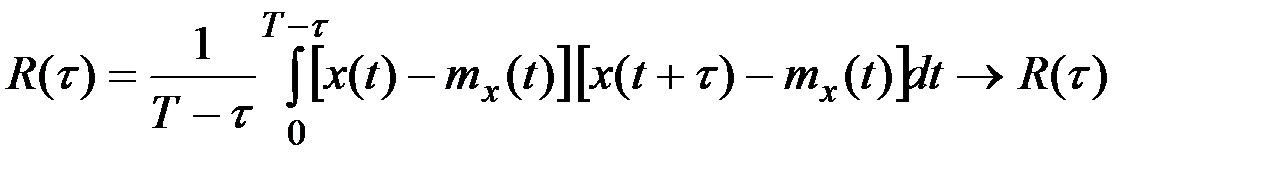при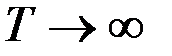 
.