– значение СФ, количество проданного товара в i–м магазине в момент времени (день) , причем ; .
Оценкой математического ожидания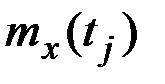 
ординаты 
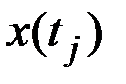является средняя арифметическая 
:
.
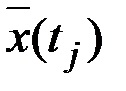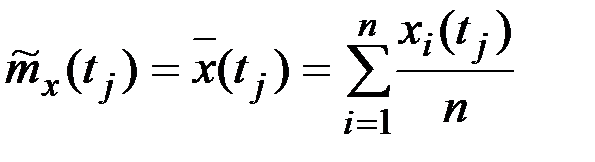За оценку математического ожидания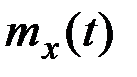 
случайной функции X(t) принимается совокупность оценок математических ожиданий ординат 
.
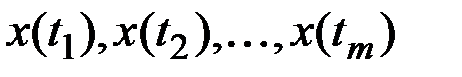За оценку дисперсии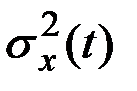 
функции X(t) принимается совокупность эмпирических дисперсий 
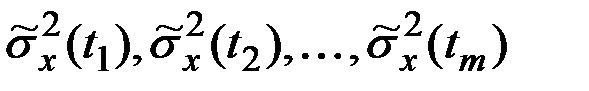, где
.
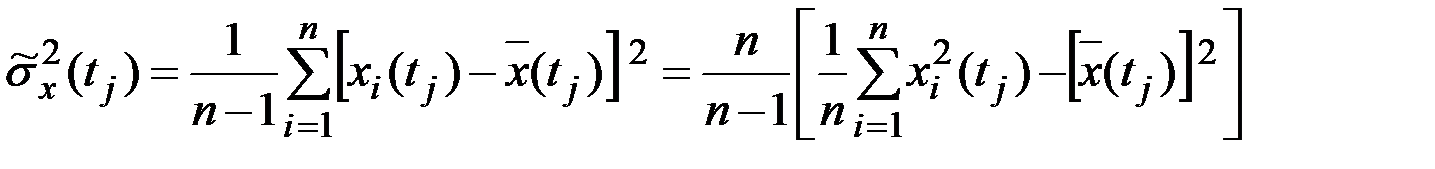Оценкой корреляционного момента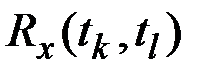 
ординат 
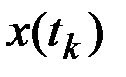и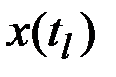 
является эмппрический корреляционный момент 
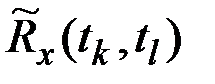, вычисляемый по формуле
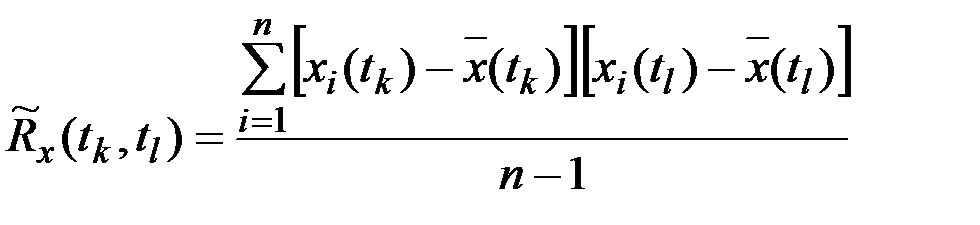
или по тождественной формуле
.
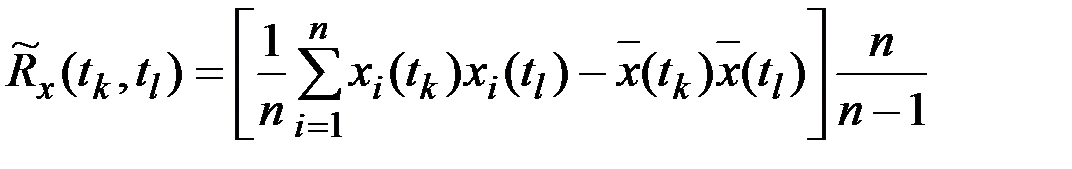За оценку корреляционной функции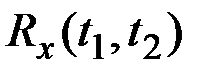 
принимается совокупность эмпирических корреляционных моментов, вычисленных для всевозможных пар из m ординат 
.
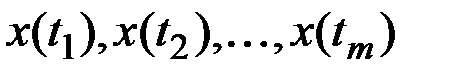За оценку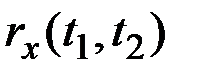 
нормированной корреляционной функции принимается совокупность эмпирических коэффициентов корреляции
,
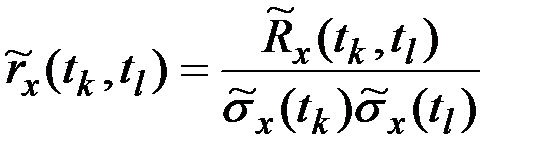вычисленных для всевозможных пар из m ординат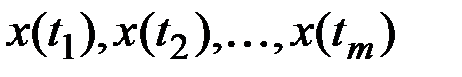 
.
Эмпирическую корреляционную функцию обычно аппроксимируют простым аналитическим выражением (для удобства дальнейших исследований).
Аппроксимирующее выражение должно отображать наиболее характерные свойства графика эмпирической функции и сглаживать случайные колебания при больших значениях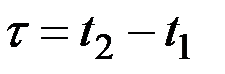 
, т.е. в точках, полученных осреднением небольшого числа данных и потому ненадёжных.
Наиболее часто встречаются следующие виды аппроксимирующих выражений:
;
.
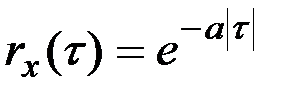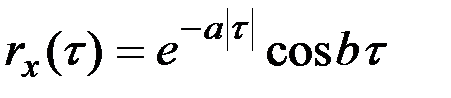Определение неизвестных параметров аппроксимирующих функций производится обычно методом наименьших квадратов.
7.2. Стационарные случайные процессы
Стационарные СФ характеризуются однородностью протекания во времени.
Предположим, что в результате проведения опытов получено несколько реализаций СФ и найдены оценки математического ожидания, дисперсии и корреляционной функции. Используя теорию статистической проверки гипотез, можно выяснить, случайны или нет изменения средних арифметических и эмпирических дисперсий ординат и изменения оценок корреляционных моментов при фиксированной разности моментов времени, для которых взяты ординаты.
Если изменения носят случайный характер, то математическое ожидание и дисперсию СФ можно считать постоянными величинами, а корреляционную функцию зависящей только от промежутка времени между ординатами, т.е. случайная функция стационарна.
Однако, при решении практических задач, как правило, исследователь ограничен небольшим числом реализаций СФ. Это может привести к тому, что теория статистической проверки гипотез, предполагающая достаточно большое число наблюдений, не подтвердит гипотезы о стационарности функции, хотя природа явления позволяет судить о том, что оно должно описываться стационарной функцией. Поэтому решить, стационарна или нет исследуемая функция, можно только изучив внутреннюю структуру исследуемого явления.