Зафиксируем некоторое значение аргумента, например, и найдём значения n реализаций для данного .
Полученные значения 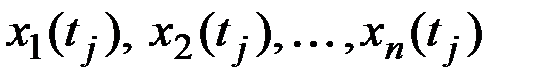 называют сечением n реализаций случайной функции при
называют сечением n реализаций случайной функции при 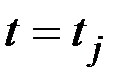 .
.
Сечение можно рассматривать как n значений, принятых случайной величиной – ординатой 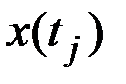 случайной функции (рис.7.1).
случайной функции (рис.7.1).
В связи с этим часто СФ определяют как множество случайных величин 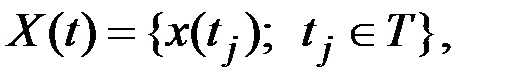 где Т – область задания СФ.
где Т – область задания СФ.
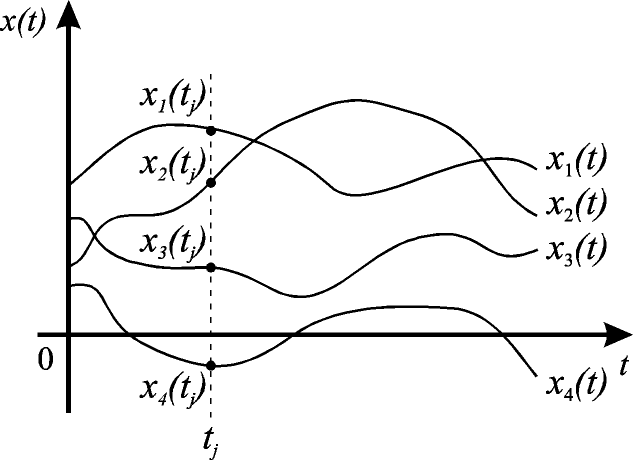
Рис.7.1. Реализации случайных функций
Строго говоря, СФ мы не можем изобразить с помощью кривой на графике – начертить мы можем лишь её конкретные реализации.
В зависимости от того принадлежат ли возможные значения аргумента t и функции X(t) дискретному множеству чисел или отрезку различают четыре типа СФ.
1. Непрерывный случайный процесс. В этом случае t и X(t) могут принимать любые значения на отрезке или на всей оси (изменение с течением времени точности настройки станка, износ инструмента).
2. Дискретный случайный процесс. В этом случае t непрерывно, а X(t) принимает дискретные значения (количество посетителей в фирме, изменение с течением времени количества машин на заправке).
3. Непрерывная случайная последовательность. Здесь t дискретно, а X(t) может принимать любые значения на отрезке или на всей оси (котировки ценных бумаг, объём реализованного товара).
4. Дискретная случайная последовательность. Аргумент t и функция X(t) дискретны (количество участников торговых сессий, количество сделок на бирже, результаты проверки изделий на брак, количество студентов на лекции).
Реализации дискретных СФ – ступенчатые функции.
Классификацию случайных процессов (функций) можно выполнить и по другим признакам.
Могут быть использованы следующие критерии: 1) зависимость или независимость свойств этих функций от начала отсчёта времени; 2) вид закона распределения СФ; 3) зависимость дальнейшего поведения СФ от её значений в настоящий и предшествующие моменты времени.
В первом случае различают стационарные и нестационарные случайные функции.
Для функций первого типа все k–мерные законы распределения зависят от взаимного расположения моментов времени, но не от самих значений этих величин. Для стационарной СФ при любом k = 1, 2, … должно выполняться равенство
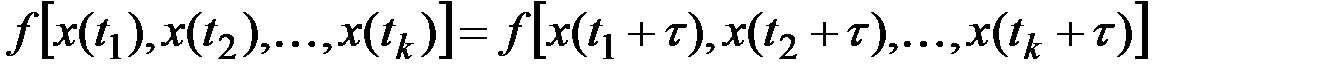 ,
,
где τ – любое число.
В частном случае, при k = 1 и k = 2, полагая 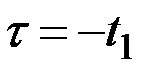 , имеем
, имеем
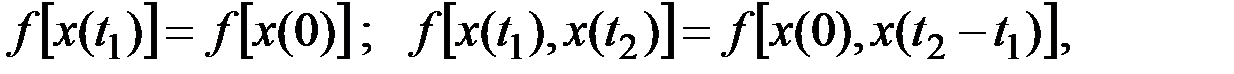
т.е. одномерный закон распределения не зависит от момента времени, для которого он рассматривается, двумерный же закон распределения зависит от разности между моментами времени и не зависит от начала отсчёта времени.
По виду закона распределения выделяются, прежде всего, нормальные (гауссовские) случайные процессы, которые имеют широкое практическое применение.
В конкретных задачах могут встречаться процессы с различными законами распределения (экспоненциальным, биномиальным, Релея, Пуассона, логнормальным, Стьюдента, 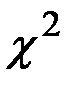 –распределением, равномерным, β–распределением, γ–распределением и др.).
–распределением, равномерным, β–распределением, γ–распределением и др.).
В третьем случае, если в каждый момент времени дальнейшее поведение функции обусловлено её состоянием в данный момент времени и не зависит от поведения функции в предшествующий период, то такая случайная функция называется марковской (по имени русского математика А.А. Маркова, впервые рассмотревшего функции такого типа).
В конкретном сечении 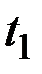 случайная функция превращается в случайную величину, которую полностью можно охарактеризовать своим законом распределения.
случайная функция превращается в случайную величину, которую полностью можно охарактеризовать своим законом распределения.
В большинстве задач одномерные законы распределения не могут служить полной характеристикой СФ, так как они не отражают взаимную зависимость её ординат.
Для получения более детальной характеристики пользуются двумерным законом: 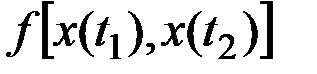 (совместным законом распределения ординат
(совместным законом распределения ординат 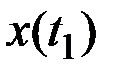 и
и 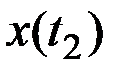 ), где
), где 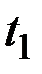 и
и 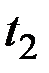 – произвольные значения аргумента СФ.
– произвольные значения аргумента СФ.
Выбрав три значения аргумента 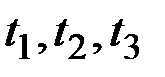 и указав трёхмерный закон распределения
и указав трёхмерный закон распределения 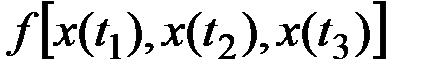 , получим ещё более подробную характеристику случайной функции.
, получим ещё более подробную характеристику случайной функции.
Совместный закон распределения 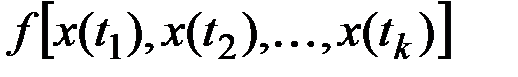 k ординат называется k–мерным законом распределения СФ.
k ординат называется k–мерным законом распределения СФ.
Случайная функция полностью определена, если заданы все k–мерные законы распределения (k = 1, 2, …).
Определение СФ с помощью k–мерных законов распределения не всегда удобно вследствие их громоздкости. Поэтому часто ограничиваются заданием вероятностных характеристик СФ.
Характеристики случайных процессов представляют собой в общем случае функции (в частном случае числа).
Математическим ожиданием процесса X(t) называется неслучайная функция 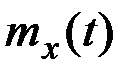 , которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения процесса:
, которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения процесса:
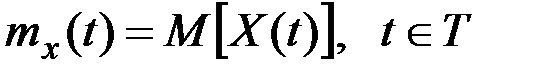 .
.
Среднее значение случайного процесса в момент времени 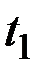 может быть найдено путём суммирования мгновенных значений каждой выборочной функции ансамбля в момент
может быть найдено путём суммирования мгновенных значений каждой выборочной функции ансамбля в момент 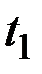 и деления этой суммы на число выборочных функций:
и деления этой суммы на число выборочных функций:
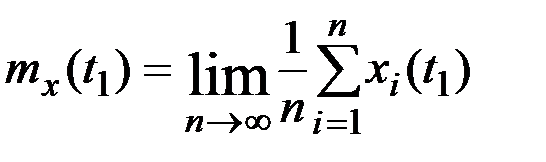 .
.
С геометрической точки зрения математическое ожидание СФ представляет собой некоторую среднюю функцию, около которой группируются и относительно которой колеблются всевозможные реализации СФ (рис.7.2).

Рис.7.2. Математическое ожидание случайного процесса
Дисперсией случайного процесса X(t) называется неслучайная функция 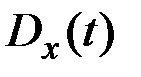 , значение которой для каждого t равно дисперсии соответствующего сечения процесса:
, значение которой для каждого t равно дисперсии соответствующего сечения процесса: 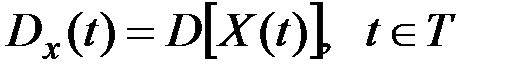 .
.
Дисперсия является мерой разброса возможных реализаций случайного процесса относительно его математического ожидания: чем больше этот разброс, тем больше дисперсия.
Функция σx(t) = 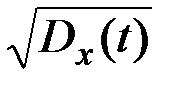 называется средним квадратическим отклонением случайного процесса X(t).
называется средним квадратическим отклонением случайного процесса X(t).
Корреляционная функция (иначе – автокорреляционная функция, АКФ) 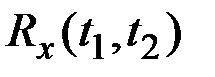 характеризует зависимость между сечениями процесса, относящимися к различным t. Это неслучайная функция двух аргументов, которая при каждой паре значений
характеризует зависимость между сечениями процесса, относящимися к различным t. Это неслучайная функция двух аргументов, которая при каждой паре значений 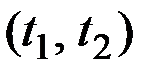 равна корреляционному моменту соответствующих сечений:
равна корреляционному моменту соответствующих сечений:
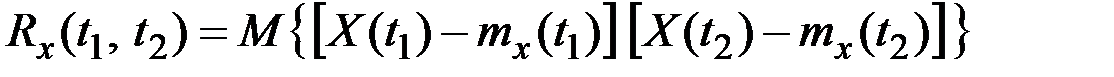 .
.
При 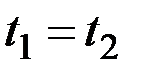 АКФ обращается в дисперсию процесса.
АКФ обращается в дисперсию процесса.
Корреляция между значениями случайного процесса в два различных момента времени определяется путём осреднения (по ансамблю реализаций) произведений отклонений от математического ожидания мгновенных значений процесса в моменты t и 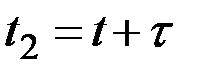 , т.е.
, т.е.
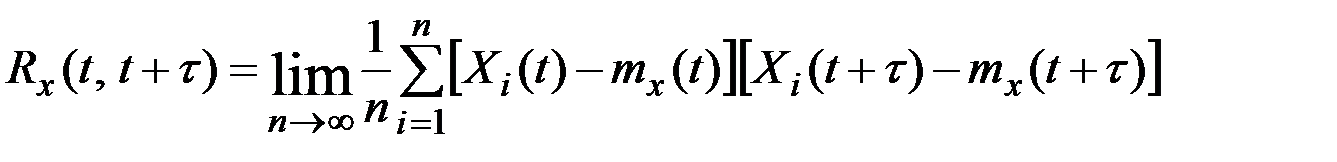 .
.
Если 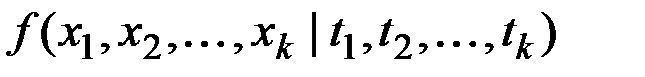 есть плотность вероятности совместного распределения ординат процесса в моменты времени
есть плотность вероятности совместного распределения ординат процесса в моменты времени 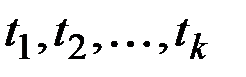 , то математическое ожидание и корреляционная функция определяются функциями
, то математическое ожидание и корреляционная функция определяются функциями 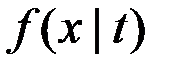 и
и 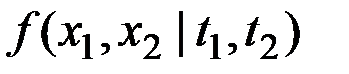 по формулам
по формулам
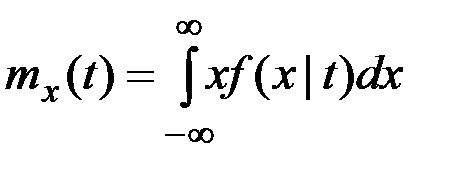 ;
;
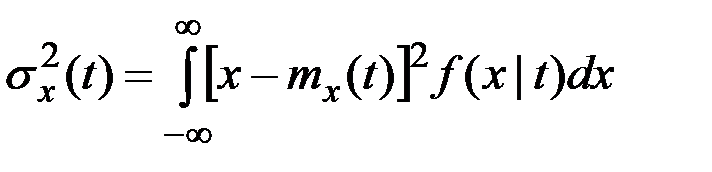 ;
;
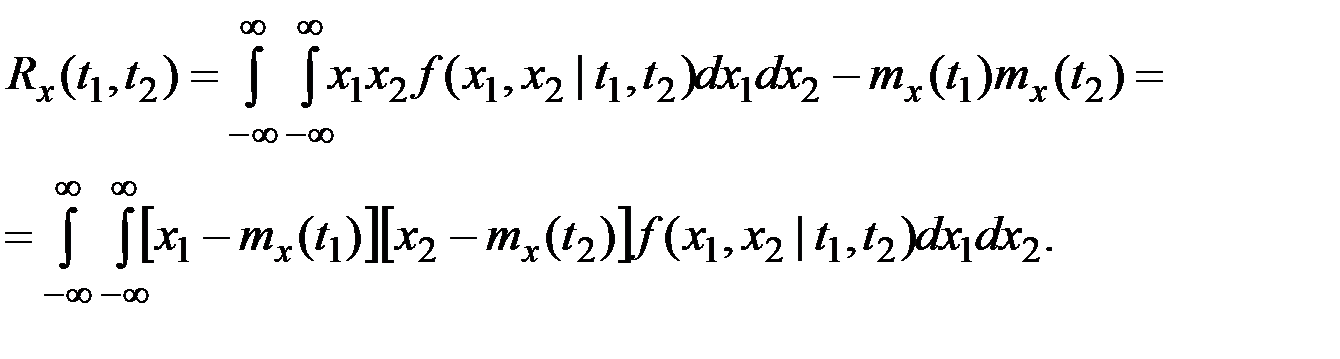
Случайная функция называется нормальной, если закон распределения системы любого числа k её сечений представляет собой k–мерный нормальный закон.
Для нормального случайного процесса совместное распределение ординат в k моментов времени (закон распределения k–го порядка) полностью определяется функциями 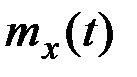 и
и 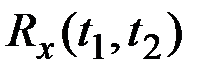 по формулам для закона распределения системы нормальных СВ, математические ожидания которых равны соответственно
по формулам для закона распределения системы нормальных СВ, математические ожидания которых равны соответственно 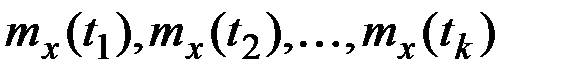 , а элементы корреляционной матрицы
, а элементы корреляционной матрицы 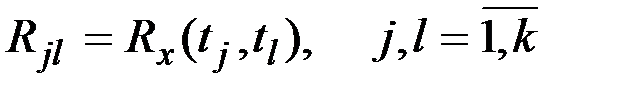 .
.
Основные свойства корреляционной функции (рис.7.3):
а) 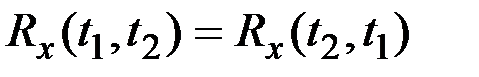 (симметричность);
(симметричность);
б) 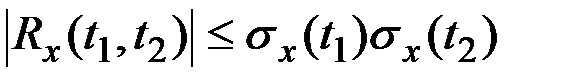 (ограниченность);
(ограниченность);
в) функция 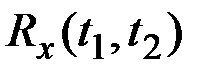 положительно определенная, т.е.
положительно определенная, т.е.
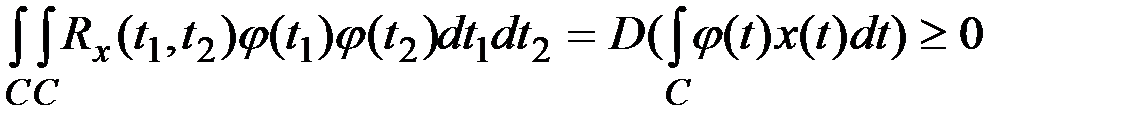 ,
,
где 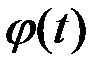 – любая функция; С – любая область интегрирования, одинаковая для обоих аргументов.
– любая функция; С – любая область интегрирования, одинаковая для обоих аргументов.
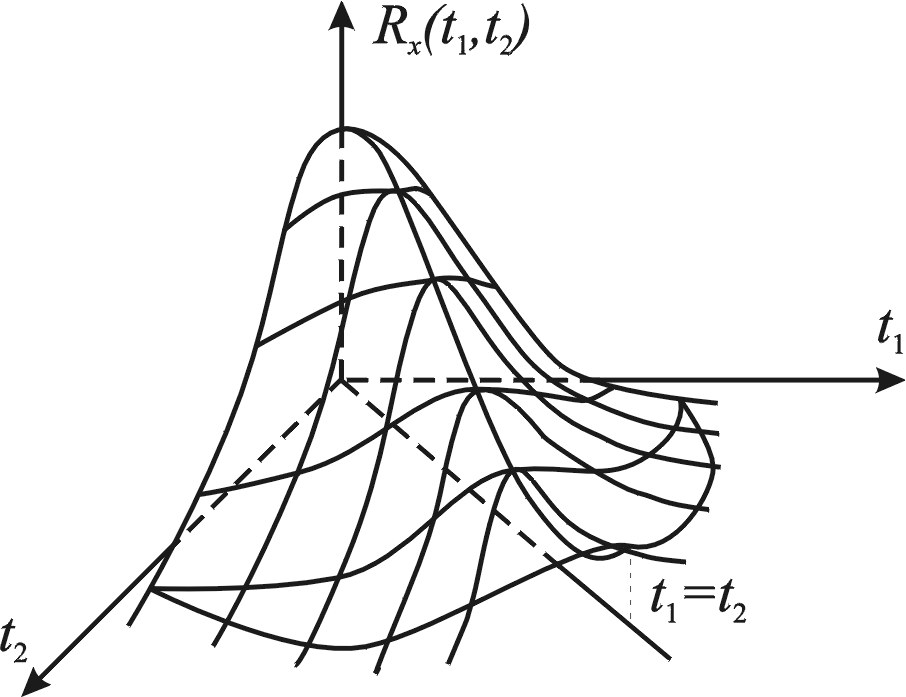
Рис.7.3. Типичный вид автокорреляционной функции процесса
Нормированная корреляционная функция представляет собой коэффициент корреляции случайных величин 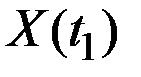 и
и 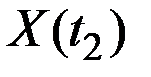 для различных сочетаний аргументов
для различных сочетаний аргументов 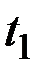 и
и 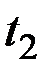 :
:
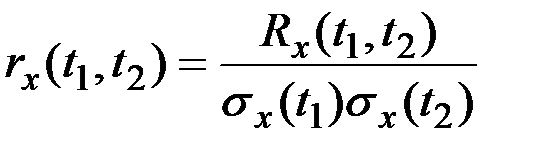 .
.
Нормированная АКФ заключена в пределах
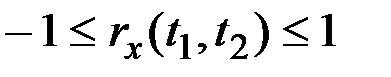 .
.
Раздел теории случайных функций, оперирующий только с моментами первых двух порядков, носит название корреляционной теории случайных функций. Многие технические и экономические задачи могут быть решены в рамках корреляционной теории.
Практически интересные задачи, требующие привлечения аппарата СФ, могут быть разбиты на 3 основные группы.
1. К первой группе относятся задачи, связанные с определением вероятностных характеристик случайных процессов по экспериментальным данным: определение корреляционной функции по известным реализациям; определение соответствующих законов распределения для ординат случайного процесса.
При решении задач этого типа используют обычные приёмы обработки опытного материала в математической статистике, но возникают некоторые специфические особенности, связанные с наличием зависимости между ординатами реализаций СФ.
2. Ко второй группе можно отнести задачи, в которых по известным свойствам СФ требуется определить те или иные вероятностные характеристики процесса.
Сюда относятся, например, определение дисперсии ординаты СФ в заданный момент времени; определение вероятности того, что ордината процесса в заданный момент времени не выйдет за пределы некоторого интервала; определение вероятности того, что процесс в течение заданного интервала изменения своего аргумента не выйдет за определенные пределы (задачи о "выбросах" процесса за заданный уровень) и другие задачи.
Для решения этих задач необходимо располагать теми или иными вероятностными характеристиками процессов, причём для решения простейших из них достаточно знать только моменты второго порядка СФ, в то время как для решения задачи о выбросах необходимо иметь более подробную информацию о свойствах СФ.
3. К третьей группе относятся задачи, связанные с определением вероятностных свойств СФ, получаемых путём применения к известным СФ (с известными вероятностными характеристиками) определённых математических операций.
Задачи подобного типа весьма распространены в технике, так как исследование поведения различных динамических систем обычно сводится к определению вероятностных характеристик СФ, получаемых на "выходе" системы по вероятностным характеристикам СФ, поступающим на "вход" системы, и динамическим свойствам самой системы.
К этому же типу задач относятся задачи экстраполирования (прогнозирования) и фильтрации СФ.
При вычислении основных характеристик СФ (математического ожидания, дисперсии и корреляционной функции) необходимо знать одномерный и двумерный законы распределения СФ, которые, как правило, неизвестны. Поэтому вместо вероятностных характеристик СФ рассматривают их оценки, вычисленные по данным наблюдений.
Пусть в результате проведения n независимых опытов получено n реализаций случайной функции X(t).
Промежуток времени 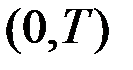 , в течение которого проводятся наблюдения, разобьём на равные интервалы точками
, в течение которого проводятся наблюдения, разобьём на равные интервалы точками 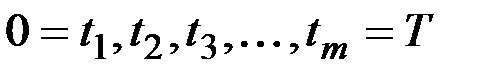 .
.
Для каждого значения аргумента 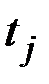 найдём значения n реализаций СФ X(t), которые запишем в табл.7.1.
найдём значения n реализаций СФ X(t), которые запишем в табл.7.1.
Таблица 7.1
Результаты наблюдений случайного процесса
| Номер наблюдения | Моменты времени наблюдений | ||||
| 1 | 2 | 3 | … | m | |
| 1 | 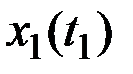
| 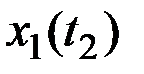
| 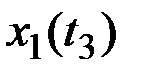
| … | 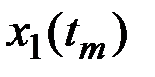
|
| 2 | 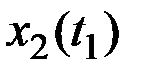
| 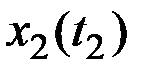
| 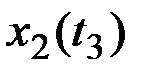
| … | 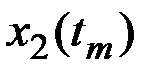
|
| … | … | … | … | … | |
| n | 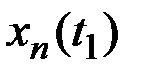
| 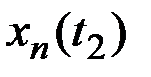
| 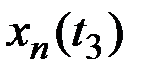
| … | 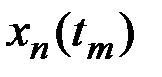
|
Здесь X – случайная величина, например, количество проданного товара за один день (в стоимостном выражении);








