Контрольные задачи к разделу 6
6.1. Ряд распределения случайной величины X представлен таблицей:
| X | –2 | 0 | 2 |
| P | ¼ | ½ | ¼ |
Найти характеристическую функцию случайной величины X.
6.2. Найдите характеристическую функцию непрерывной случайной величины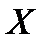 
, имеющей плотность распределения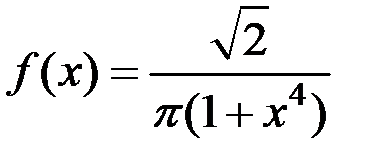 
6.3. Найдите характеристическую функцию случайной величины 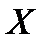, ряд распределения которой представлен в таблице:
|
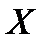
| 0 | 1 | 2 | 3 |
| 
| 
| 
| 
|
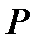
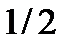
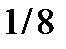
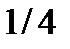
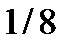
6.4. Найти характеристическую функцию случайной величины X, имеющей равномерное на интервале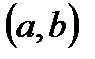 
распределение:
6.5. Найдите плотность распределения случайной величины, имеющей характеристическую функцию
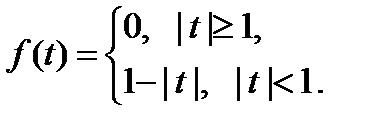
6.6. Найдите характеристическую функцию непрерывной случайной величины 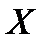, имеющей плотность распределения
6.7. Независимые случайные величины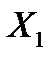 
и 
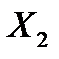распределены по экспоненциальному закону с параметрам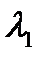и 
и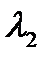 
. Найти характеристическую функцию случайной величины 
.
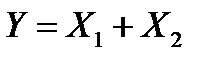6.8. Случайная величина X имеет плотность распределения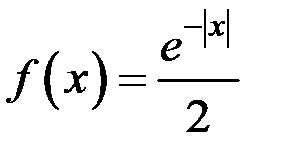 
. Найти характеристическую функцию случайной величины X.
6.9. Найдите характеристическую функцию случайной величины 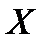, ряд распределения которой представлен в таблице:
|
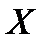
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
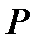
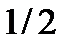
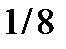
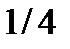
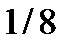
6.10. Найдите характеристическую функцию непрерывной случайной величины 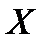, имеющей плотность распределения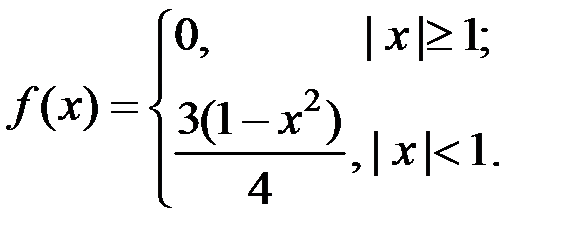 
6.11. Найдите характеристическую функцию неотрицательной целочисленной случайной величины 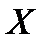, распределение которой задается вероятностями
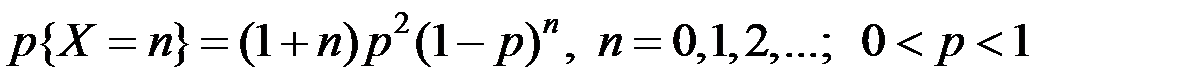
6.12. Случайная величина 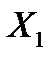распределена равномерно на интервале 
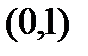, а случайная величина 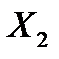имеет стандартное нормальное распределение. Найдите характеристическую функцию случайной величины 
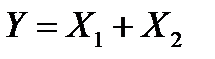, если известно, что 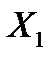и 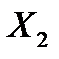являются независимыми.
6.13. Найти закон распределения случайной величины, характеристическая функция которой равна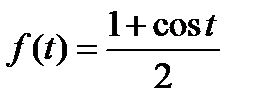 
.
6.14. Найдите характеристическую функцию случайной величины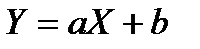 
, где Х – случайная величина, имеющая плотность распределения
.
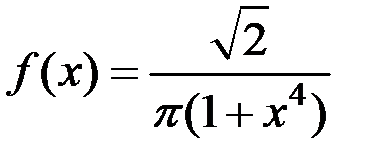6.15. Найдите математическое ожидание и дисперсию случайной величины Х, имеющей характеристическую функцию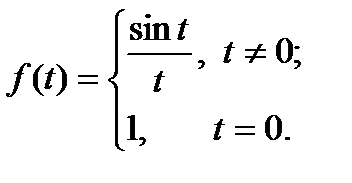 
6.16. Найти математическое ожидание и дисперсию случайной величины X, имеющей характеристическую функцию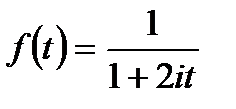 
.
6.17. Найти закон распределения случайной величины X, характеристическая функция которой равна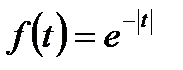 
.
7. СЛУЧАЙНЫЕ ПРОЦЕССЫ
7.1. Основные понятия и характеристики случайных процессов
Все наблюдаемые процессы, характеризующие физические явления, можно классифицировать в самом общем виде как детерминированные и недетерминированные.
К детерминированным относятся процессы, которые могут быть описаны точными математическими соотношениями.
Случайным процессом (или случайной функцией, СФ) называется процесс, который в результате опыта может принять тот или иной конкретный вид, причём заранее неизвестно, какой именно.
Конкретный вид, принимаемый процессом в результате опыта, называется реализацией или выборочной функцией случайного процесса.
В зависимости от целей исследования аргументом СФ могут быть время, пространственная координата и другие неслучайные параметры.
На практике встречаются также СФ, зависящие не от одного, а от нескольких аргументов. Например, температура есть функция четырёх аргументов: трёх пространственных координат и времени.
Если независимый аргумент – время, то говорят о случайном процессе, если пространственная координата или другие неслучайные параметры, то говорят о случайной функции.
Будем рассматривать случайные функции одного аргумента t .
Пусть произведено n независимых опытов, в результате которых получено n реализаций. Например, при обработке детали на её поверхности остаются неровности, являющиеся результатом неравномерности процесса резания, пластических деформаций детали и других причин, повторяющихся нерегулярно.
Если сделать сечения детали перпендикулярно к обрабатываемой поверхности, то кривые профиля отличаются друг от друга.
Обозначим реализации СФ через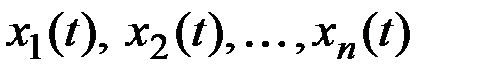 
.
Каждая реализация есть обычная (неслучайная) функция.