Характеристической функцией (ХФ) действительной скалярной СВ Х называется математическое ожидание величины , рассматриваемое как комплексная функция действительной переменной t .
ХФ – есть интеграл Фурье от функции плотности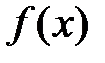 
:
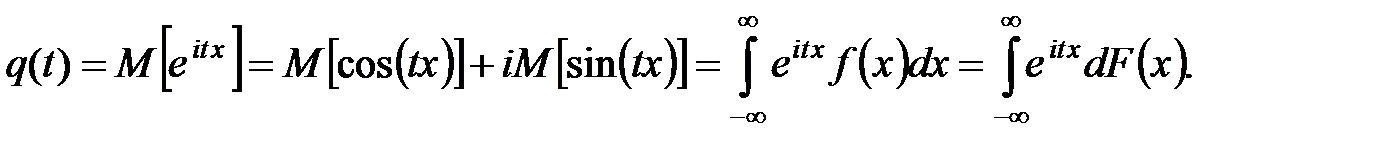
Здесь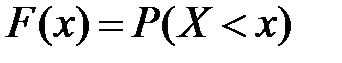 
– функция распределения СВ Х.
Для дискретной СВ Х
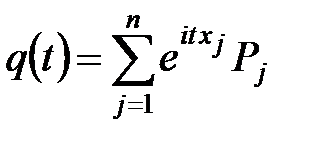, где 
.
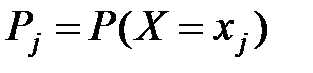Для векторной величины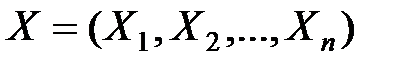 
ХФ определяется в виде
.
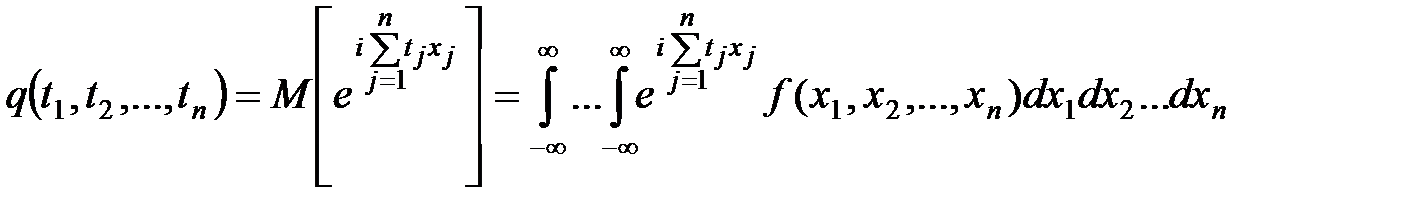Или в векторной форме
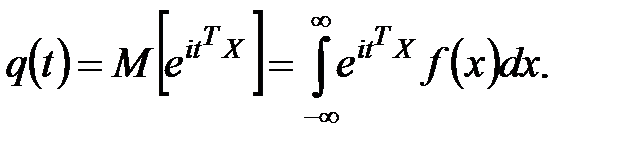
Здесь t, Х – векторы–столбцы размерности n;
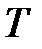– индекс транспонирования.
Свойства характеристических функций
1. Так как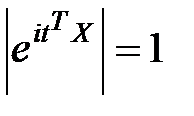 
для всех действительных t, то любая действительная случайная величина имеет ХФ.
2. ХФ непрерывна; для ХФ выполняются следующие соотношения:
.
3. ХФ положительно определенная функция, т.е. для любых значений 
, 
,..., 
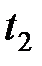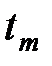переменной t и любых комплексных 
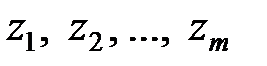выполняется условие:
,
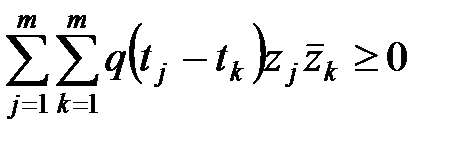где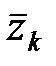 
– комплексно сопряженная величина.
Действительно, из определения характеристической функции и свойств математических ожиданий следует:
.
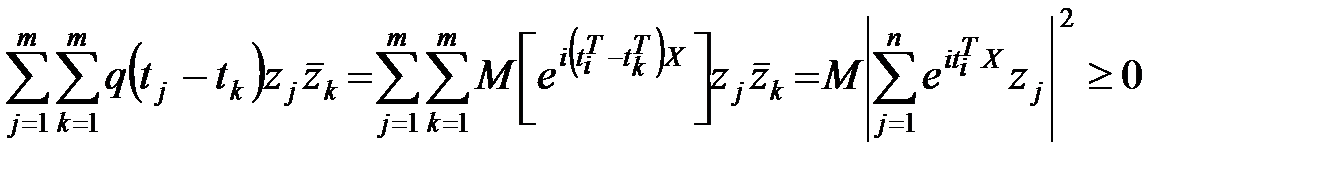Можно доказать, что любая положительно определенная функция 
, у которой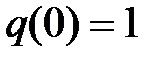 
, может быть XФ (теорема Бохнера – Хинчина).
4. Характеристическая функция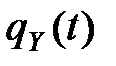 
величины 
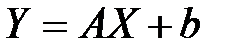, полученной в результате линейного преобразования 
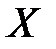, выражается через ХФ 
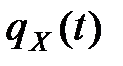формулой
.
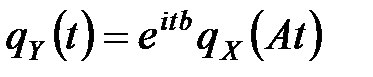Действительно, по определению (для одномерной величины) имеем
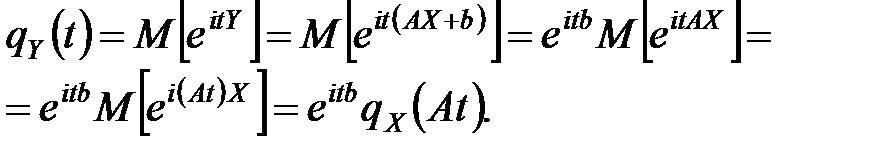
5. Характеристическая функция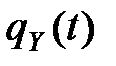 
суммы независимых случайных величин 
равна произведению их ХФ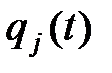 
:
;
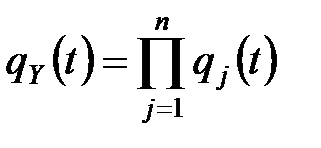где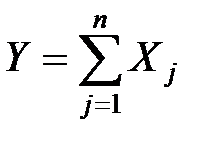 
.
Можно доказать, что СВ 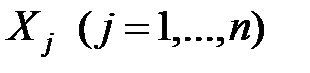независимы тогда и только тогда, когда их совместная XФ равна произведению их ХФ.
6. ХФ СВ полностью и однозначно определяет ее распределение.
Функция плотности выражается через ХФ в виде интеграла Фурье
.
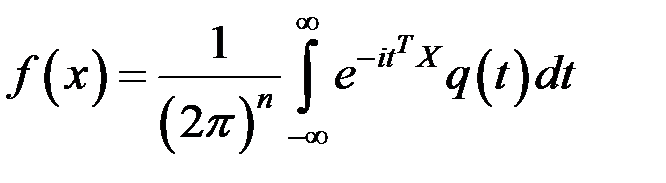Для одномерного случая имеем соотношение
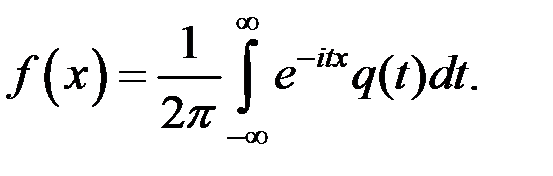
Эти формулы определяет плотность как для непрерывных, так и для дискретных или непрерывно–дискретных СВ, так как плотность дискретной СВ можно выразить через импульсную дельта–функцию Дирака:
.
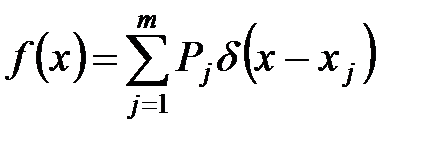Дельта–функция имеет следующие свойства:
, 
,
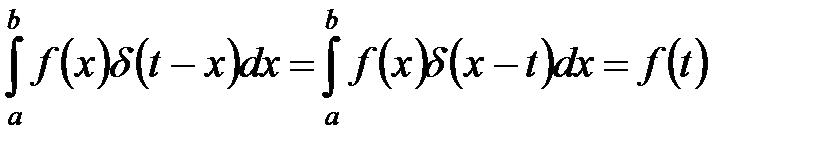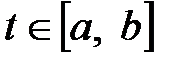а при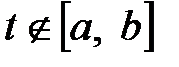 
оба интеграла равны нулю;
,
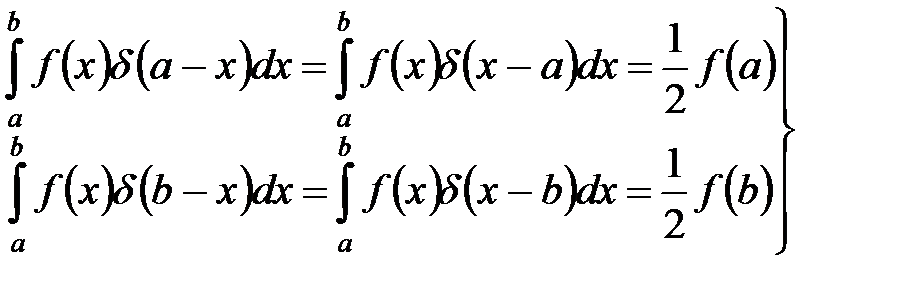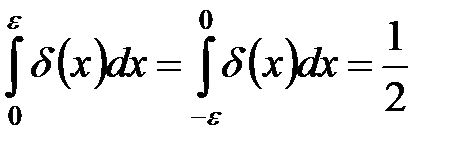при любом 
.
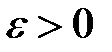Функция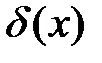 
есть предел единичного прямоугольного импульса при стремлении ширины импульса к нулю.
Дельта–функция Дирака для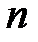 
–мерного вектора 
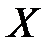представляется интегралом Фурье:
;
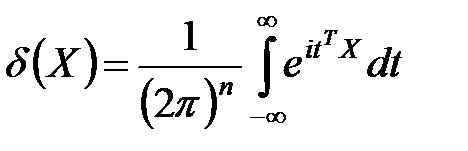(здесь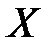 
, t – матрицы–столбцы).
Пример 6.1. Найти ХФ для распределений: биноминального, Пуассона равномерного, нормального.
Решение.
1) ХФ дискретной величины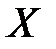 
с возможными значениями 
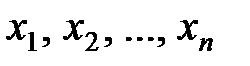и их вероятностями 
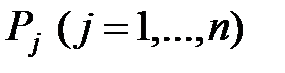определяются формулой:
.
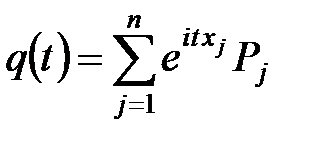Тогда для биномиального распределения имеем:
.
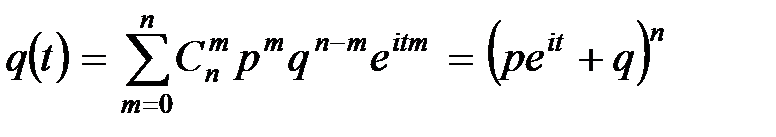2) Для распределения Пуассона имеем
,
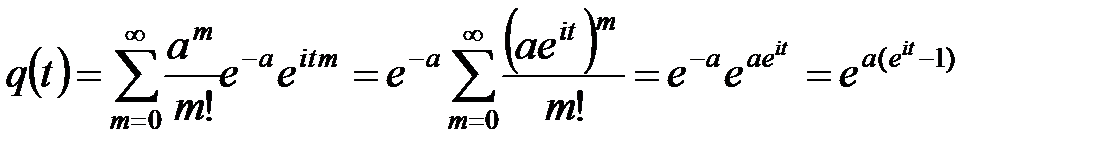так как
.
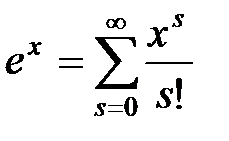3) Для равномерного распределения в интервале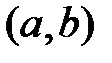 
.
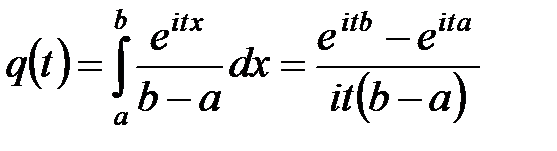В частности, ХФ равномерно распределенной СВ на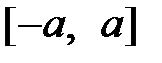 
:
.
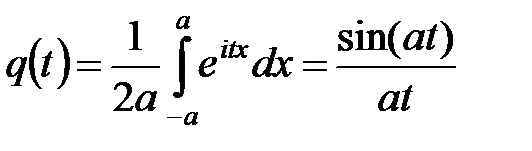4) Для нормальной СВ имеем:
,
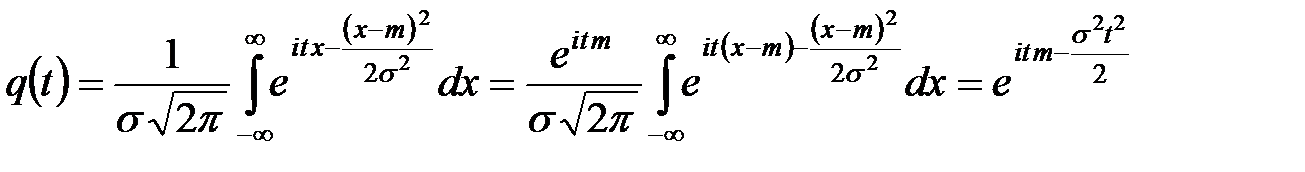так как
.
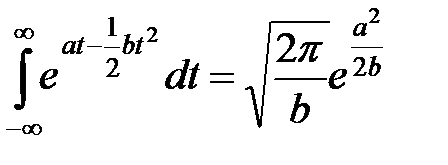Для n–мерного нормального распределения случайного вектора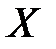 
.
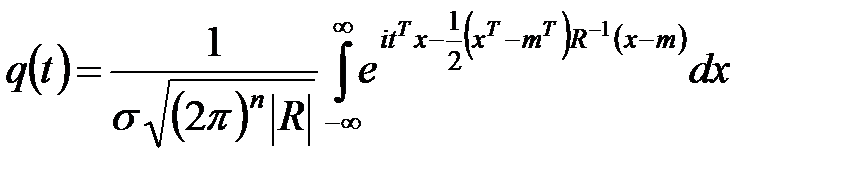Так как
,
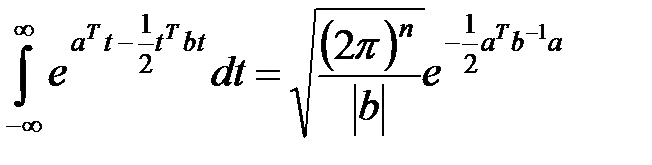то получим
.
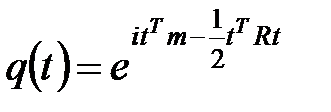6.3. Использование характеристических функций
Начальные моменты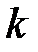 
– го порядка 
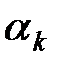вычисляются через 
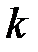–ую производную ХФ в нуле:
.
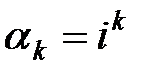
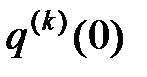Центральные моменты СВ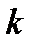 
–го порядка 
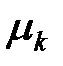выражаются через ХФ следующим образом:
.
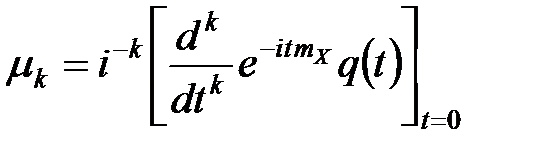ХФ можно вычислить через моменты по формулам Маклорена
; 
,
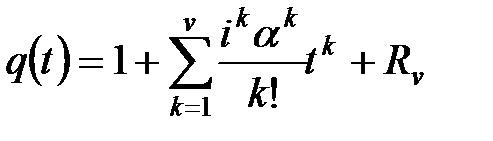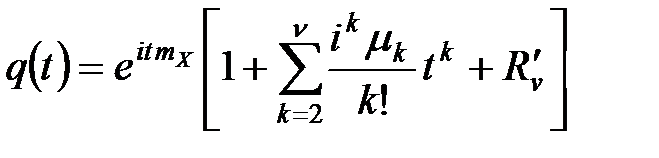где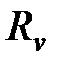 
– остаточный член при использовании моментов до порядка v включительно. Он имеет порядок 
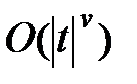, такой же порядок имеют и производные 
.
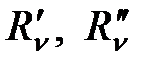Аналогично для n–мерного случайного вектора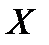 
формулы для моментов имеют вид:
;
.
.
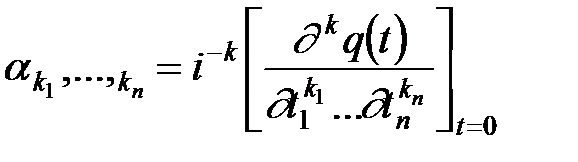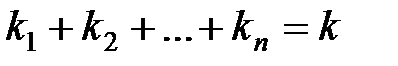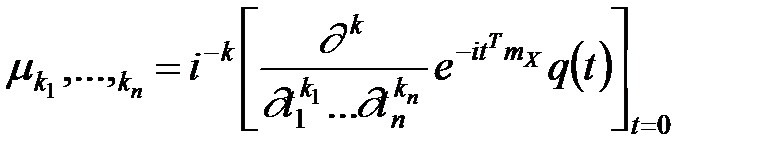Характеристическая функция для n–мерного случайного вектора 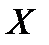определяется выражениями
,
.
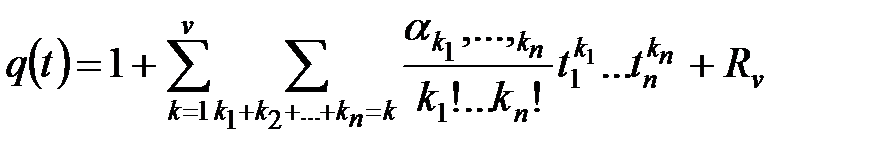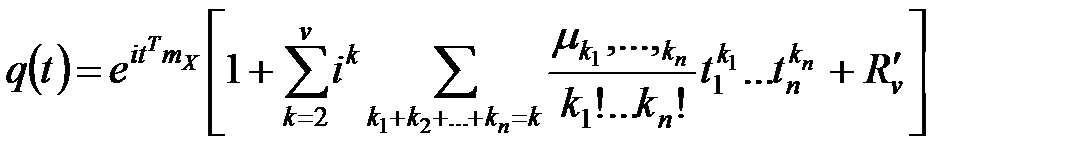Внутренние суммы распространяются на все значения
, 
,
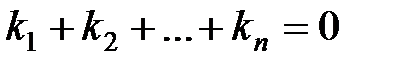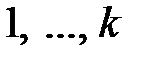сумма которых равна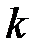 
.
Указанные выше соотношения дают два простых и удобных способа вычисления моментов СВ: способ дифференцирования ХФ и способ разложения ХФ по степеням t.
Можно доказать, что если распределение СВ полностью сосредоточено в ограниченной области, то ее моменты всех порядков существуют и полностью определяют ее распределение.
Пример 6.2. Получить выражение для всех центральных моментов нормальной СВ.
Решение. Для нормальной СВ ХФ имеет вид
.
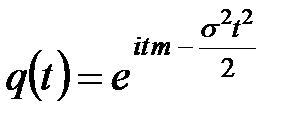С другой стороны ХФ выражается через центральные моменты по соотношению
.
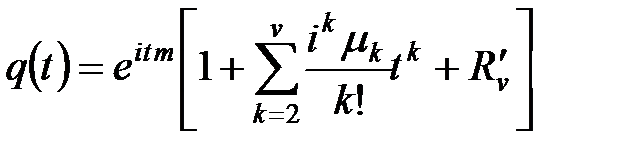Приравнивая эти выражения и учитывая, что
,
,
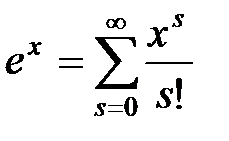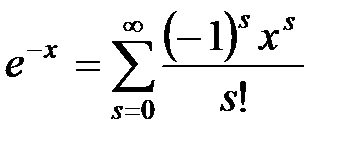получим:
;
;
; 
;
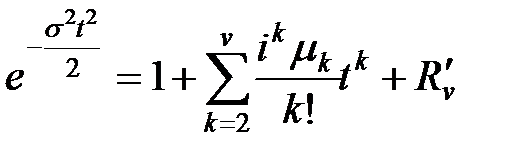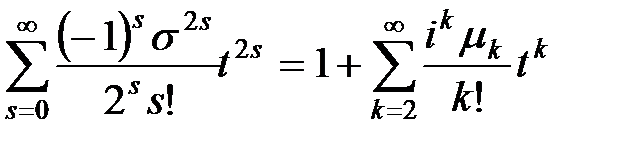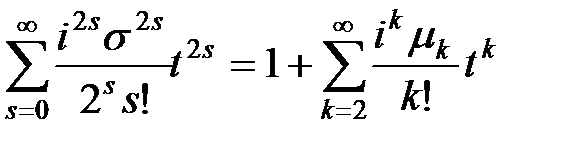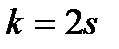При определении плотности функции случайного аргумента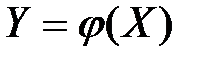 
часто целесообразно использовать ХФ. Согласно определению ХФ 
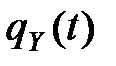функции 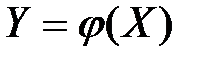определяется формулой:
.
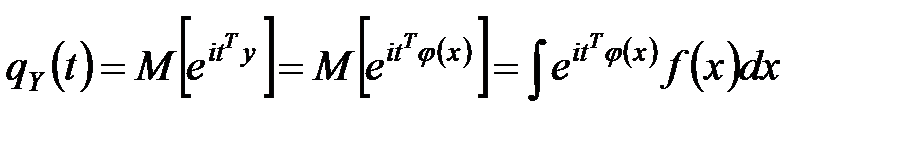Здесь 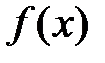– плотность СВ 
.
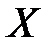Определив таким путем ХФ величины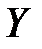 
можно затем найти ее плотность
.
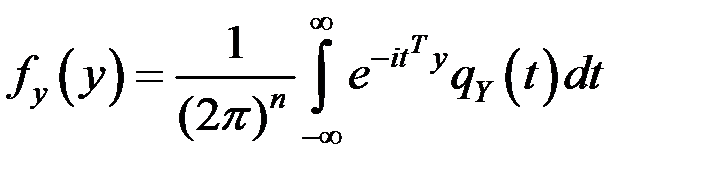Наибольшую пользу аппарат ХФ приносит при исследовании распределения сумм независимых СВ.
Пример 6.3. Найти ХФ суммы двух независимых распределений Пуассона с параметрами a и b.
Решение. ХФ суммы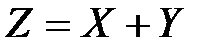 
двух независимых СВ равна произведению соответствующих ХФ. Поэтому получаем:
.
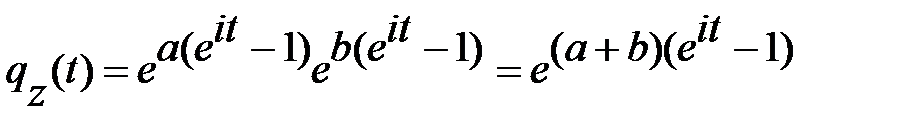Полученное выражение соответствует форме ХФ пуассоновского распределения с параметрами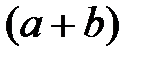 
, то есть сумма двух законов Пуассона дает снова закон Пуассона с соответствующими параметрами.
Пример 6.4. Найти распределение суммы всех независимых СВ 
и 
, распределенных равномерно в интервалах 
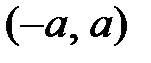и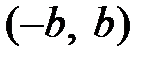 
соответственно 
.
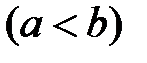Решение. Имеем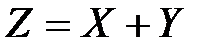 
.
Тогда
.
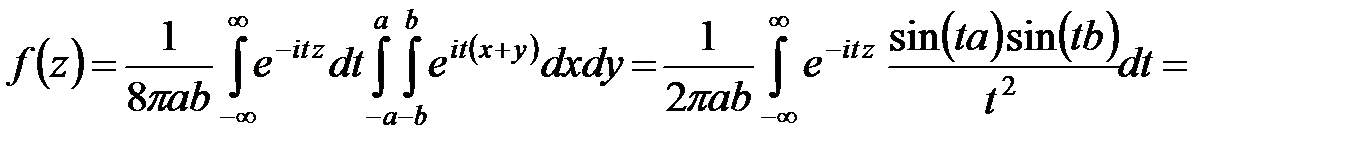
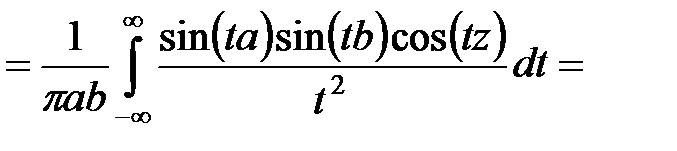
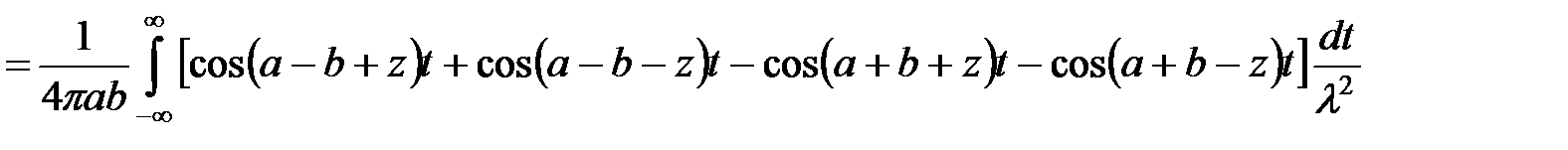Отсюда на основании известной формулы
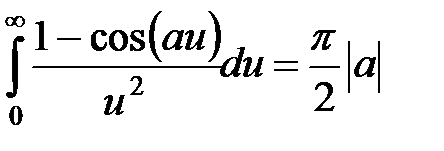
получаем:
.
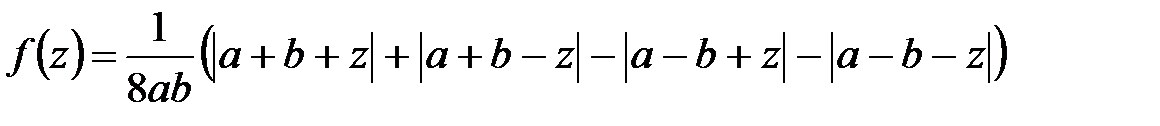6.3. Семиинварианты
В некоторых случаях удобно пользоваться разложением по степеням t не самой ХФ, а ее логарифма. Если существуют моменты скалярной СВ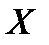 
до порядка v включительно, то на основании формулы Маклoрена имеем:
.
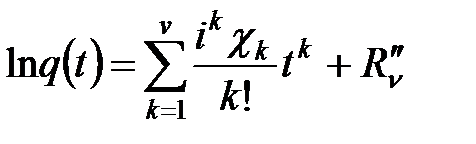Коэффициенты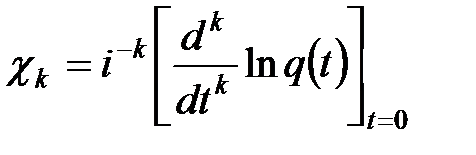 
, 
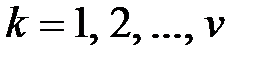называются семиинвариантами или кумулянтами СВ 
.
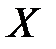Выразив производные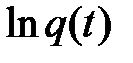 
через соответствующие производные ХФ, можно выразить семиинварианты СВ через ее моменты, и наоборот.
Если воспользоваться формулой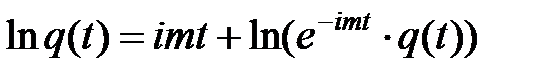 
и принять во внимание выражение центральных моментов через ХФ, то получим соотношения семиинвариантов СВ через ее математическое ожидание и центральные моменты:
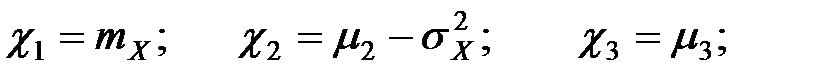
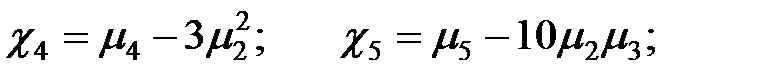
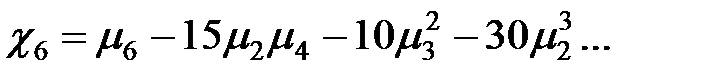
Для n–мерного случайного вектора X формула Маклорена дает:
.
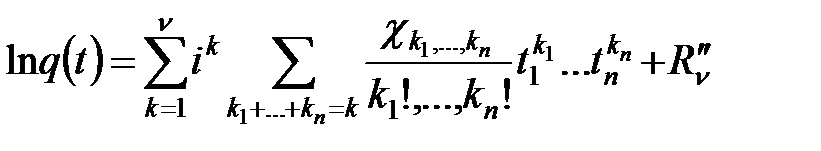Коэффициенты
, 
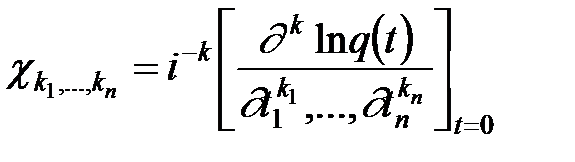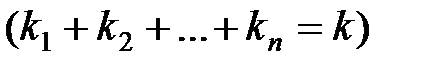
называются семиинвариантами или кумулянтами случайного вектора X.
Cемиинварианты порядка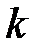 
выражаются через моменты до порядка 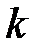включительно и наоборот.
Для нормальной СВ все семиинварианты выше второго порядка равны нулю. Следовательно, семиинварианты СВ, начиная с третьего порядка характеризуют отклонение её распределения от нормального.
Семиинварианты суммы независимых СВ равны суммам соответствующих семиинвариантов слагаемых.
Связь семиинвариантов и начальных моментов выражается формулой
.
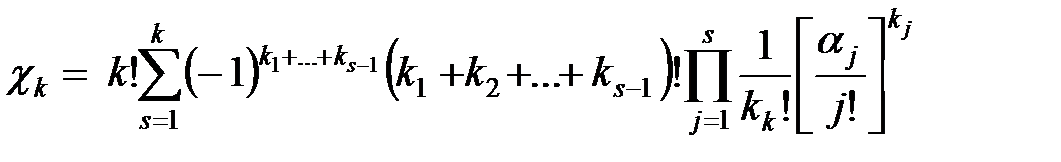Суммирование производится по всем целым неотрицательным решениям уравнения:
.
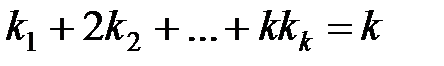