Если же и вероятность р не мала, то для подсчёта искомой вероятности нужно обратиться к формуле Бернулли.
Формула Пуассона применяется в случае, когда при большом числе испытаний n вероятность наступления события в каждом испытании весьма мала, а число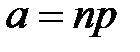 
невелико (не больше 10).
2. Интегральная теорема Лапласа (Муавра–Лапласа).
Если число независимых опытов n велико (порядка сотни), то вероятность появления события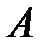 
не менее 
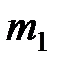и не более 
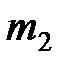раз определяется по формуле:
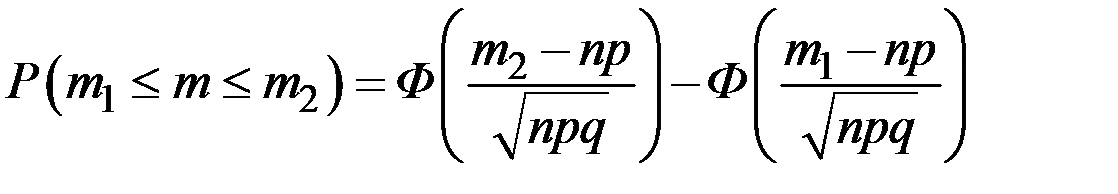, где 
.
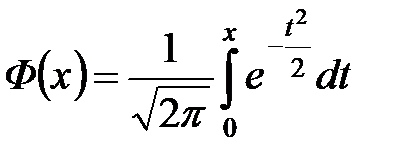Из интегральной теоремы Муавра–Лапласа следует, что вероятность того, что относительная частота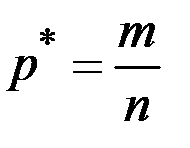 
события отклоняется от его вероятности в отдельном испытании р по абсолютной величине не более, чем на 
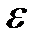, определяется по формуле
.
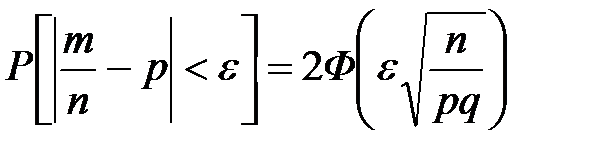Пример 5.7. Время настройки прибора имеет экспоненциальное распределение со средним значением 0,5 минут. Определить вероятность того, что на настройку 100 приборов потребуется не менее 57 минут.
Решение. Используем центральную предельную теорему для суммы 100 случайных величин с одинаковым законом распределения. Тогда
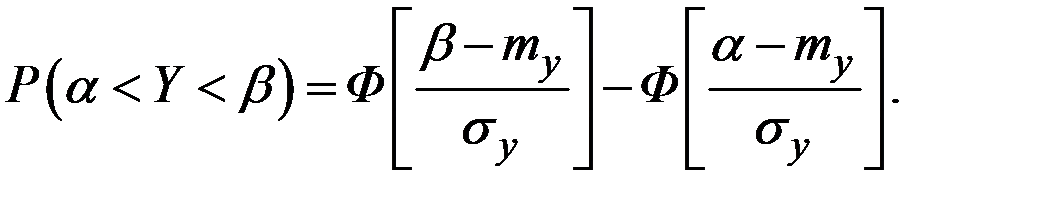
Для наших условий имеем:
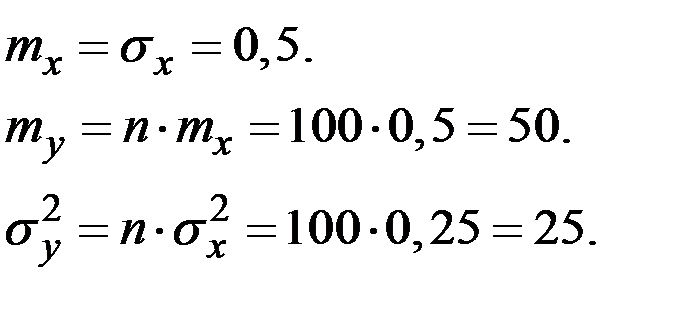
Тогда искомая вероятность
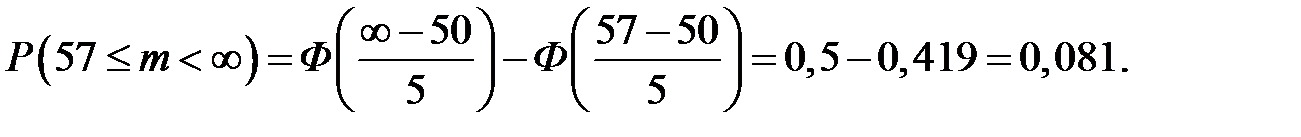
Пример 5.8. Двое играют в следующую игру. Игрок А подбрасывает игральную кость. Если доля выпавших шестёрок отличается от 1/6 менее, чем на 0,01, выигрывает игрок А, в противном случае выигрывает игрок В. При какой количестве подбрасываний выигрыш игрока А оказывается вероятнее, чем выигрыш игрока В?
Решение.
1. Используем формулу Бернулли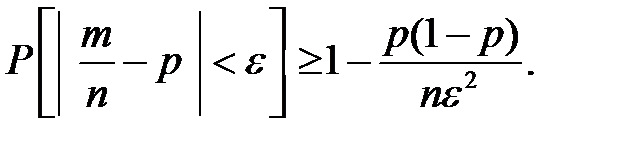 
Получаем
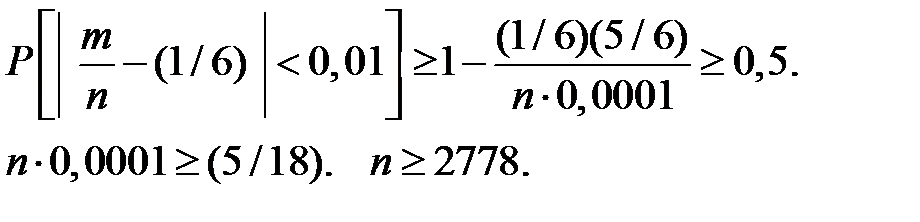
2. Из интегральной теоремы Муавра–Лапласа следует, что вероятность того, что относительная частота 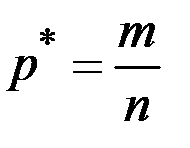события отклоняется от его вероятности в отдельном испытании р по абсолютной величине не более, чем на 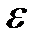, определяется по формуле
.
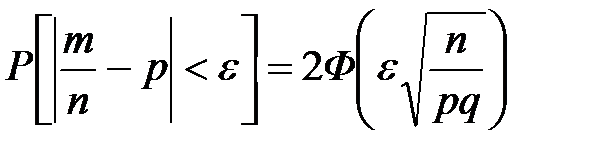Получаем
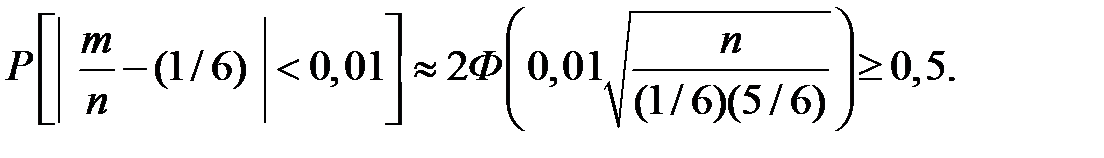
Функция Лапласа равна 0,25 при значении аргумента 0,67.
Тогда
. 
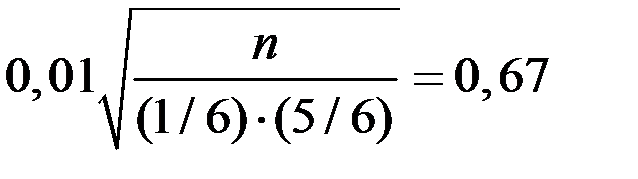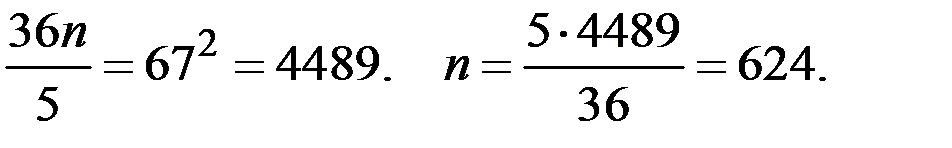
Пример 5.9. 4 станка производят детали из стали марки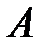 
, 6 других – из стали марки 
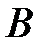. Определить вероятность того, что из 500 взятых деталей количество деталей из стали марки 
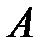будет заключено в пределах от 180 до 220.
Решение. Воспользуемся неравенством Чебышёва для оценки нижней границы искомой вероятности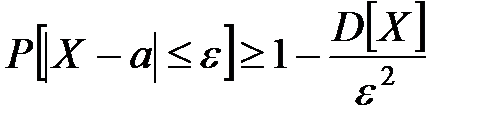 
.
Имеем параметры
.
.
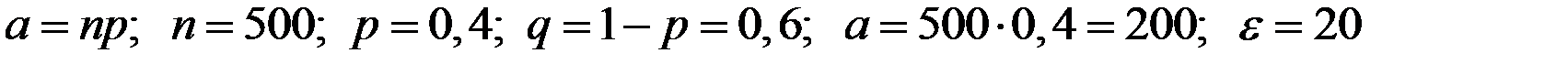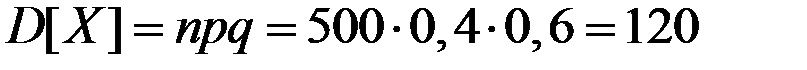Получаем нижнюю оценку искомой вероятности:
.
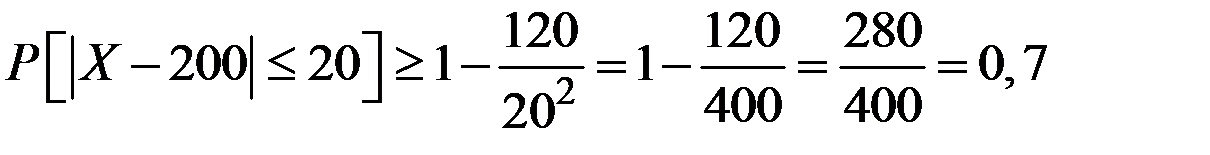С другой стороны, эту вероятность можно более точно вычислить (оценить) по теореме Муавра–Лапласа:
,
.
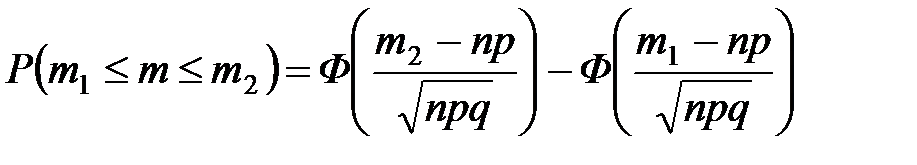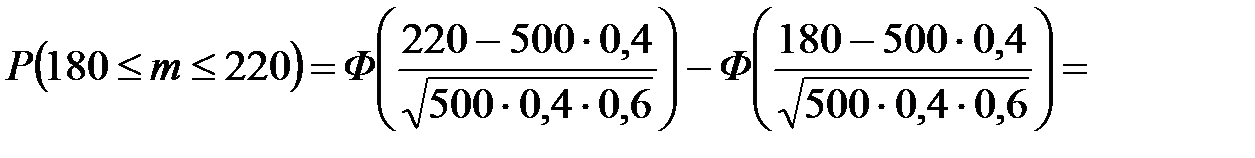
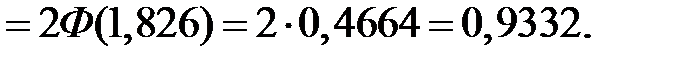
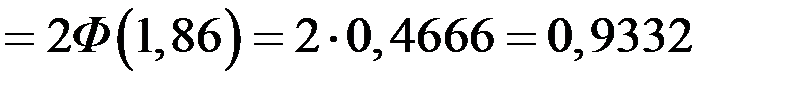5.3. Решение типовых задач главы 5
Пример 5.10. Среднее значение скорости ветра в данной местности равно 16 км/час. Оценить вероятность того, что в данной местности скорость ветра (при одном наблюдении) не превышает 80 км/час.
Решение. По первой форме неравенства Чебышёва находим
.
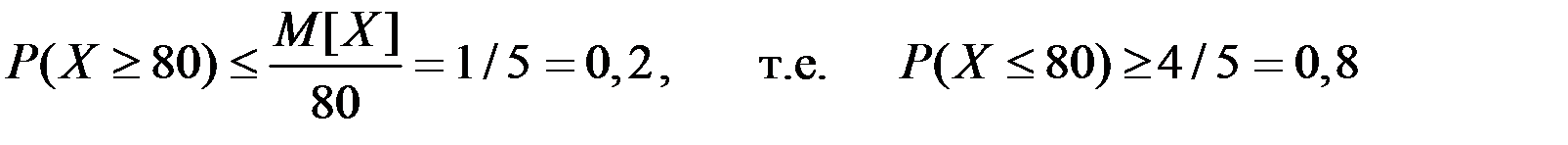Пример 5.11. В страховой компании (фирме) застраховано 8 тысяч лиц одного возраста и одной социальной группы. Вероятность смерти в течение года для каждого лица равна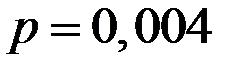 
. Каждый застрахованный в начале года вносит 30 долларов страховой премии, и, в случае смерти, его родственники получают от фирмы 5 тысяч долларов.
Найти вероятность того, что: 1) фирма разорится (будут убытки);
2) фирма получит прибыль, не меньшую чем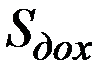 
долларов.
Вычислить эту вероятность для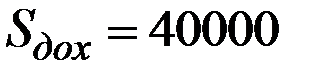 
и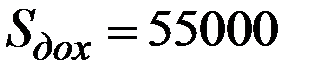 
.
Решение. Страховой фонд компании составил (8000 человек)∙(30 долл.) = 240000 долл.
Вероятность убытков для страховой фирмы (когда израсходуется весь собранный фонд) есть вероятность смерти в течение года более чем 240000/5000 = 48 застрахованных.
Пусть m – число умерших за рассматриваемый период времени.
Тогда по формуле Муавра–Лапласа имеем вероятность смерти в течение года более чем 48 застрахованных.
У нас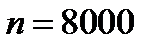 
; 
; 
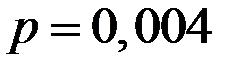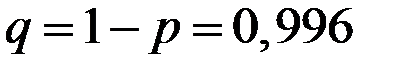. Тогда
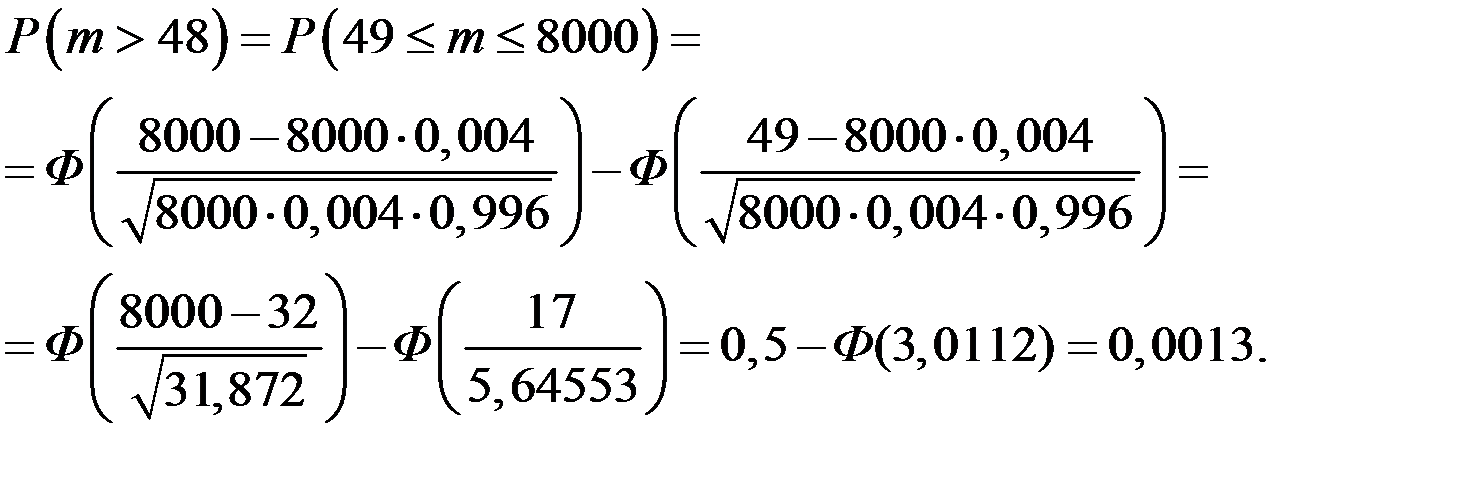
Получение прибыли фирмой возможно, если в течение года из застрахованных умрёт не более чем
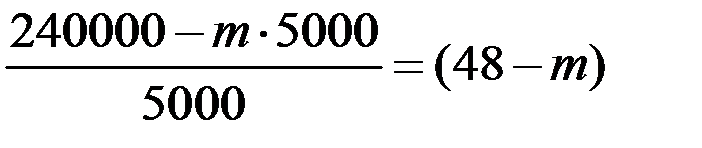человек.
Прибыль (доход фирмы) в этом случае выражается зависимостью
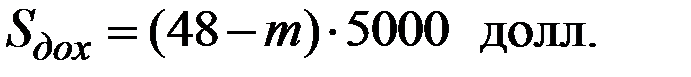
Для получения заданного дохода 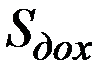количество умерших должно быть не более величины
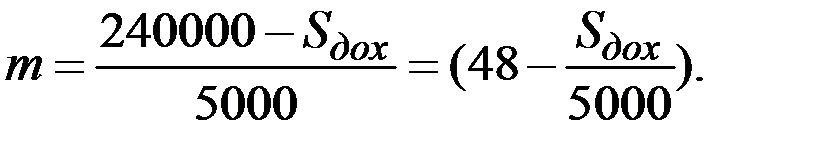
При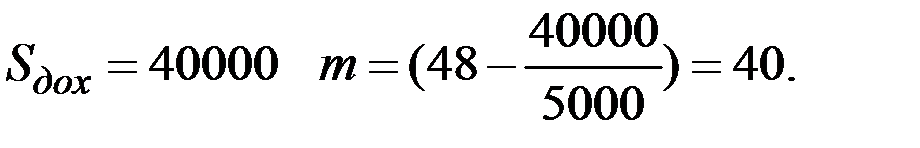 
Вероятность получения фирмой указанной прибыли определяется соотношением для количества умерших:
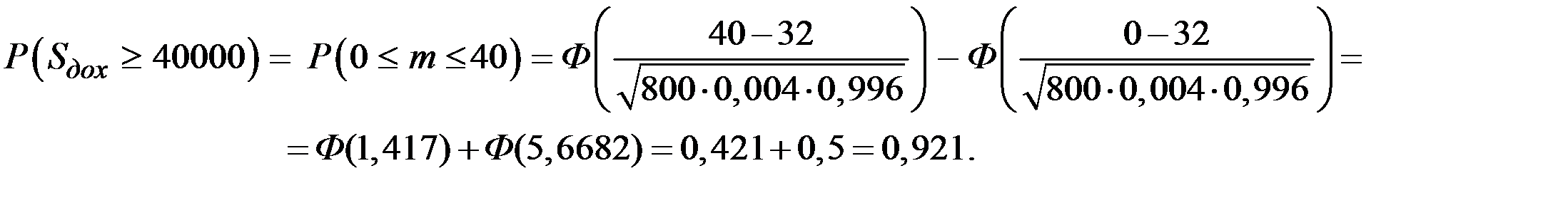
При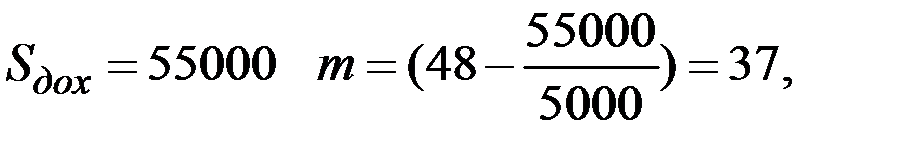 
тогда:
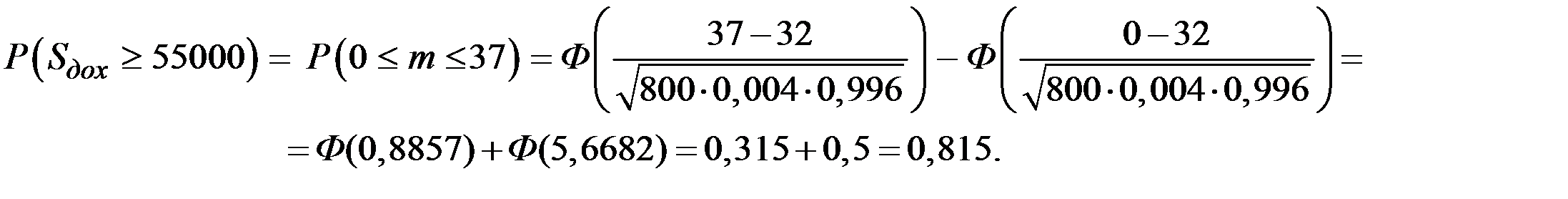
Пример 5.12. Вероятность изделию быть бракованным равна 0,05. Сколько изделий надо взять, чтобы с вероятностью не меньшей 0,9 среди них оказалось не менее 50 бракованных?
Решение. Необходимо найти число n, удовлетворяющее интегральной формуле Муавра–Лапласа
P(50 Ј m Ј n) =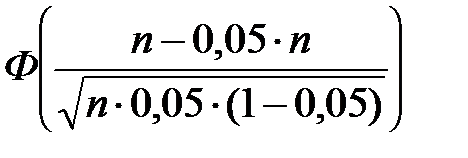 
– 
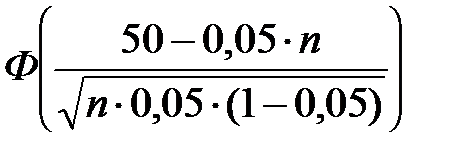і 0,9 .
Оценим значение
= 
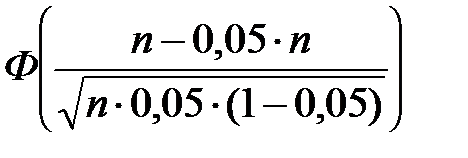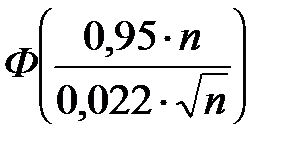» Ф(4,3 
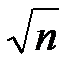) і Ф(30) » 0,5.
Тогда 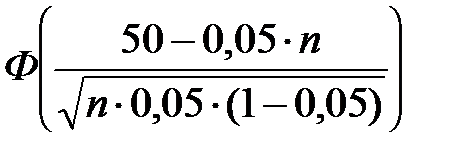Ј – 0,4.
По таблице функции Лапласа находим, что Ф(х) = – 0,4 при х = 1,28.
Поэтому получаем соотношение
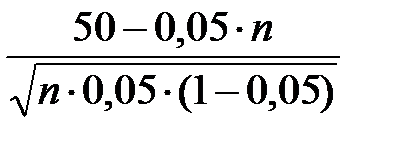Ј 1,28
или
0,05Ч n – 0,282Ч 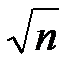– 50 і 0.
Решая последнее неравенство, находим n і 1196, то есть следует взять не менее 1196 изделий.
Пример 5.13. Станок–автомат производит детали высшего качества с вероятностью 0,8. Сколько надо произвести деталей, чтобы с вероятностью 0,90 гарантировать производство 75 деталей высшего качества?
Решение. Необходимо найти число n, удовлетворяющее интегральной формуле Муавра–Лапласа
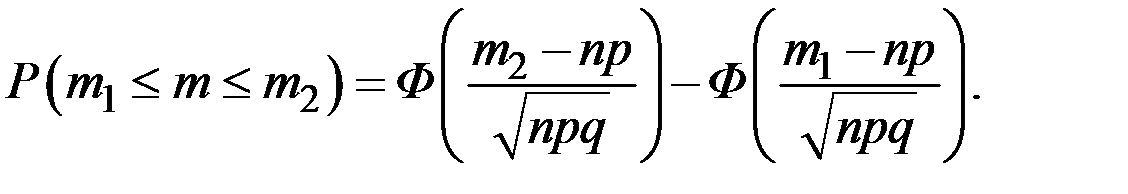
Имеем параметры
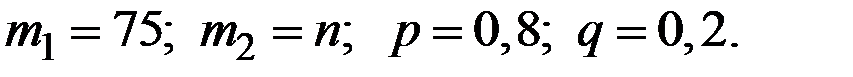
Тогда имеем соотношение
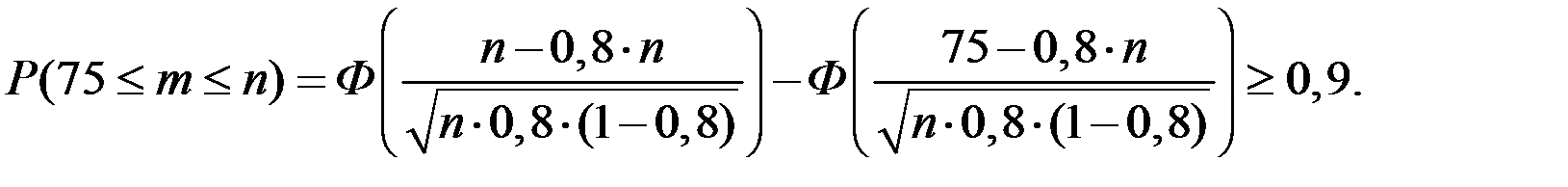
Оценим значение при n > 75
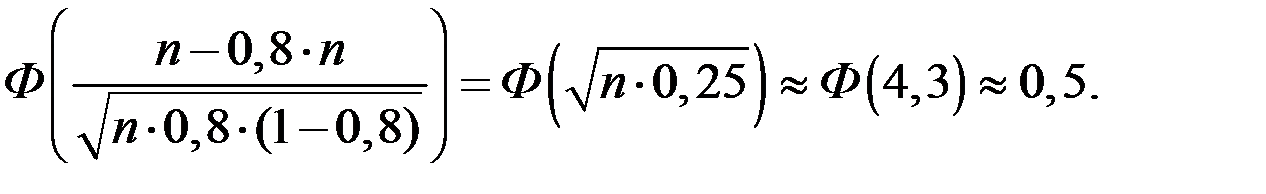
Тогда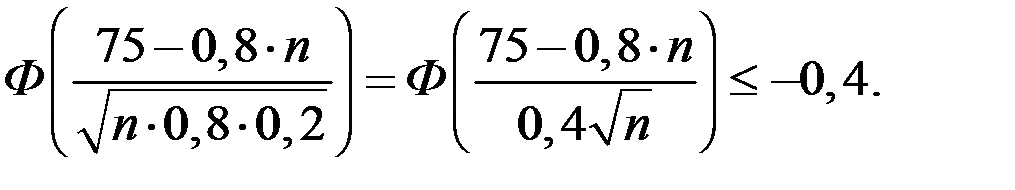 
По таблице функции Лапласа находим, что Ф(х) = – 0,4 при х = 1,28.
Поэтому получаем граничное соотношение
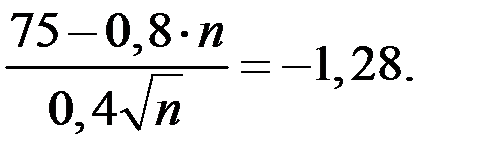
Сводим это соотношение к решению квадратного уравнения.
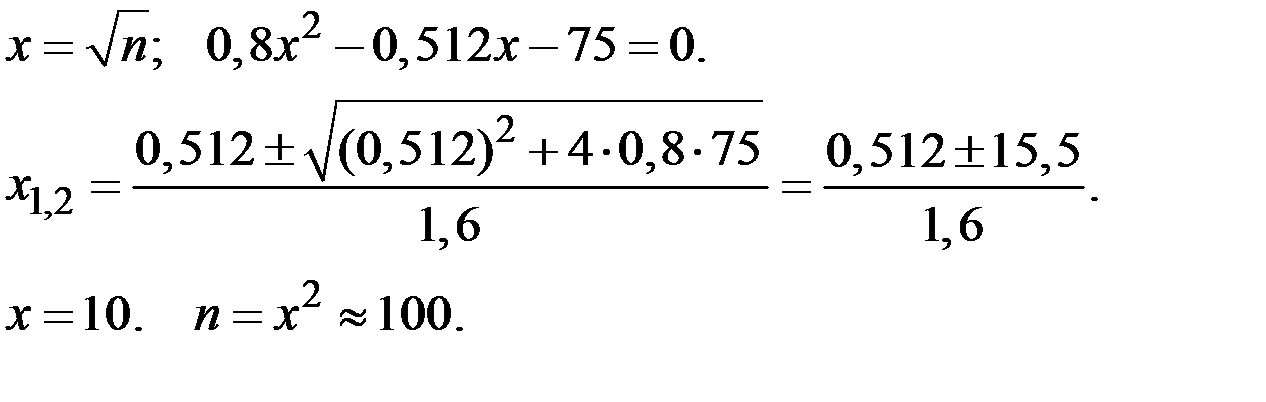
Следует произвести не менее 100 деталей.
Пример 5.14. Три станка, производительности которых соотносятся как 5:3:2, производят детали на общий конвейер. Определить вероятность того, что из 240 деталей, взятых случайным образом с конвейера, деталей, произведённых вторым станком, будет от 60 до 70.
Решение. Искомую вероятность определяем по интегральной формуле Муавра–Лапласа:
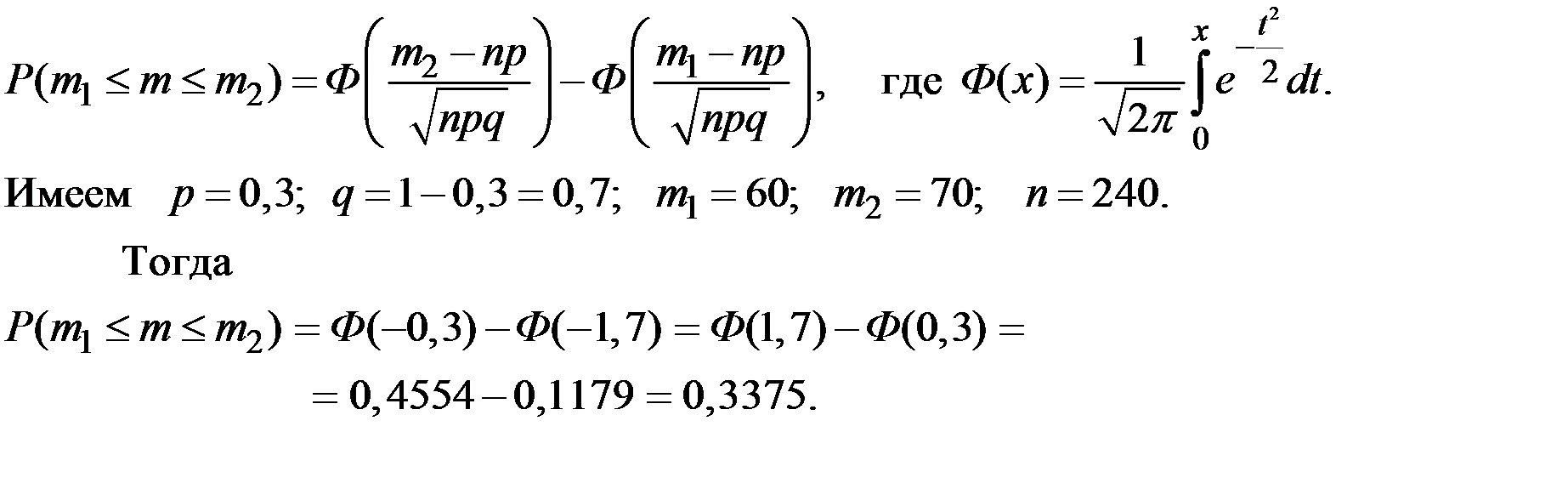
Пример 5.15. Известно, что вероятность опоздания ежедневного поезда на станцию равна 0,2. Какова вероятность того, что в течение 200 дней поезд опоздает на станцию: 1) 50 раз; 2) от 15 до 45 раз?
Решение. Целесообразно использовать формулы Муавра–Лапласа.
1. Локальная теорема Лапласа (Муавра–Лапласа).
Если число независимых опытов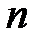 
велико, то
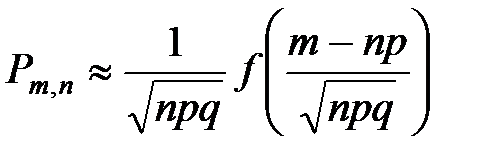, где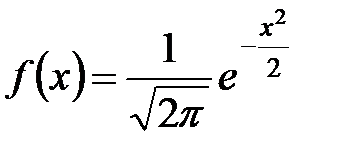 
.
Вероятность того, что событие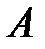 
в n опытах произойдёт ровно m раз, вычисляется через нормированную плотность нормального закона.
По локальной теореме Муавра–Лапласа получаем
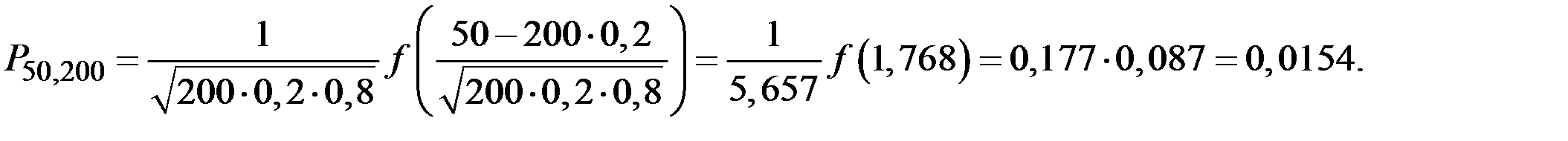
2. Интегральная теорема Лапласа (Муавра–Лапласа).
Если число независимых опытов n велико, то вероятность появления события 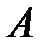не менее 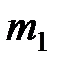и не более 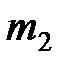раз определяется по формуле:
,
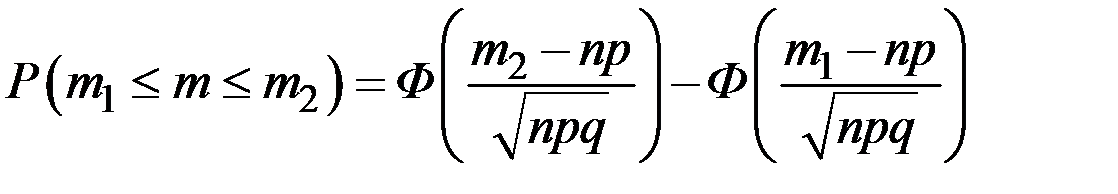где .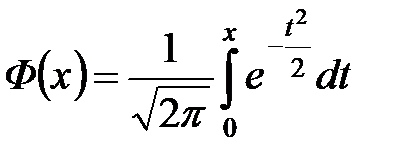
По интегральной теореме Муавра–Лапласа получаем:
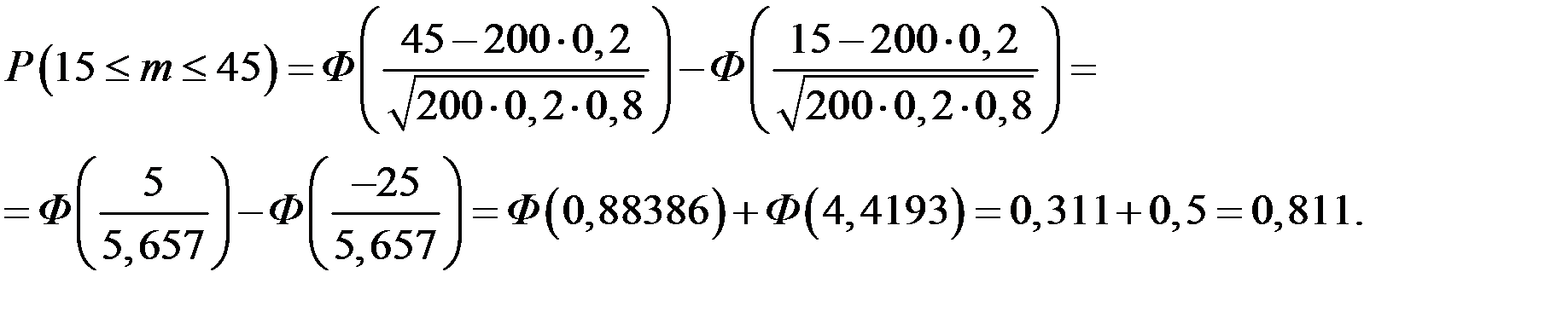
Контрольные задачи к главе 5
5.1. Среднее потребление электроэнергии в мае в некотором населённом пункте составляет 350000 кВт.ч. Оцените с помощью первого неравенства Чебышёва вероятность того, что потребление электроэнергии в мае текущего года в этом населённом пункте превысит 106 кВт.ч.
5.2. Найти вероятность того, что при 720 бросаниях игральной кости «шестёрка» выпадает от 100 до 130 раз.
5.3. Среднее квадратическое отклонение погрешности изменения курса самолёта равно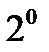 
. Считая математическое ожидание погрешности измерения равным нулю, оцените с помощью второго неравенства Чебышёва вероятность того, что погрешность одного измерения курса самолёта превысит 
.
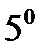5.4. Вероятность появления события A в одном опыте равна 0,5. Можно ли с вероятностью, большей 0,97, утверждать, что число появлений события A в 1000 независимых опытов будет в пределах от 400 до 650?
5.5. Средний расход воды в населённом пункте составляет 50000 литров в день. Оценить вероятность того, что в этом населённом пункте в данный день расход воды не превысит 150000 литров.
5.6. Вероятность наступления события A в каждом испытании равна 2/3. Используя неравенство Чебышёва, оценить вероятность того, что в 10000 испытаний отклонение относительной частоты события A от вероятности его появлений не превзойдёт 0,01.
5.7. Среднее квадратическое изменение курса акции компании в течение одних биржевых торгов составляет 0,3%. Оценить вероятность того, что на ближайших торгах курс изменится более чем на 3%.
5.8. Отделение банка обслуживает в среднем 100 клиентов в день. Оценить вероятность того, что сегодня в отделении банка будет обслужено не более 200 клиентов.
5.9. Электростанция обслуживает сеть на 1600 электроламп, вероятность включения каждой из которых равна 0,9. Оценить вероятность того, что число ламп, включённых в сеть вечером, отличается от своего математического ожидания не более чем на 100 (по абсолютной величине).
5.10. Вероятность того, что акции, переданные на депозит, будут востребованы, равна 0,08. Оценить с помощью неравенства Чебышёва вероятность того, что среди 1000 клиентов от 70 до 90 востребуют свои акции.
5.11. Среднее значение длины детали 50 см, а дисперсия – 0,1. Оценить с помощью неравенства Чебышёва вероятность того, что случайно взятая деталь окажется по длине не менее 49,5 см и не более 50,5 см. Уточнить вероятность того же события, если известно, что длина случайно взятой детали имеет нормальный закон распределения.
5.12. В течение времени t эксплуатируются 500 приборов. Каждый прибор имеет надёжность 0,98 и выходит из строя независимо от других. Оценить с помощью неравенства Чебышёва вероятность того, что доля надёжных приборов отличается от 0,98 не более чем на 0,1 (по абсолютной величине).
5.13. Вероятность сдачи в срок всех экзаменов студентом факультета равна 0,7. Оценить с помощью неравенства Чебышёва вероятность того, что доля сдавших в срок все экзамены из 2000 студентов заключена в границах от 0,66 до 0,74.
5.14. В среднем 10% работоспособного населения некоторого региона – безработная. Оценить с помощью неравенства Чебышёва вероятность того, что уровень безработицы среди обследованных 10000 работоспособных жителей города будет в пределах от 9 до 11% включительно.
5.15. Сколько нужно провести измерений, чтобы с вероятностью, равной 0,9973, утверждать, что погрешность средней арифметической результатов этих измерений не превысит 0,01, если измерение характеризуется средним квадратическим отклонением, равным 0,03?
5.16. Случайная величина Х является средним арифметическим из n независимых одинаково распределённых случайных величин, дисперсия каждой из которых равна 5. Оцените, какое число слагаемых n нужно взять для того, чтобы с вероятностью не менее 0,9973 случайная величина Х отклонялась от своего среднего не более чем на 0,01.
5.17. Среднее квадратическое отклонение погрешности изменения курса самолёта равно 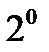. Считая математическое ожидание погрешности измерения равным нулю, оцените с помощью второго неравенства Чебышёва вероятность того, что погрешность одного измерения курса самолёта превысит .
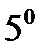5.18. Случайная величина Х является средним арифметическим из 3200 независимых случайных величин, причём каждое слагаемое имеет математическое ожидание 3 и дисперсию 2. Оценим вероятность того, что Х попадает в интервал (2,925, 3,075).
5.19. Производится выборочное обследование партии электрических лампочек. Среднее квадратическое отклонение времени горения лампочки равно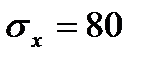 
ч. Из всей партии наудачу выбирается 400 лампочек. Оценить вероятность того, что среднее время горения лампочки будет отличаться от наблюдаемого среднего времени горения выбранных 400 лампочек не более чем на 10 ч.
5.20. Три станка, производительности которых соотносятся как 3:2:1,производят детали на общий конвейер. Определить вероятность того, что из 200 деталей, взятых случайным образом с конвейера, деталей, произведённых вторым станком будет от 50 до 70.
5.21. 3 станка производят детали из стали марки A, 7 других – из стали марки B. Определить вероятность того, что из 400 взятых деталей количество деталей из стали марки A будет заключено в пределах от 100 до 130.
5.22. Отделение банка обслуживает в среднем 100 клиентов в день. Оценить вероятность того, что сегодня в отделении банка будет обслужено более 150 клиентов.
5.23. Три станка, производительности которых соотносятся как 5:3:2, производят детали на общий конвейер. Определить вероятность того, что из 200 деталей, взятых случайным образом с конвейера, деталей, произведённых вторым станком будет от 50 до 65.
5.24. Вероятность появления некоторого события в каждом из 800 независимых испытаний равна 1/4. Воспользовавшись вторым неравенством Чебышёва, оцените вероятность того, что число Х появлений этого события заключено в пределах от 150 до 250.
5.25. Найти вероятность того, что при 430 бросаниях игральной кости «шестёрка» выпадает от 50 до 90 раз.
5.26. Три станка, производительности которых соотносятся как 4:3:1, производят детали на общий конвейер. Определить вероятность того, что из 260 деталей, взятых случайным образом с конвейера, деталей, произведённых первым станком будет от 60 до 80.
5.27. 4 станка производят детали из стали марки A , 7 других – из стали марки B. Определить вероятность того, что из 440 взятых деталей количество деталей из стали марки A будет заключено в пределах от 120 до 220.
5.28. Среднее потребление электроэнергии за месяц в летний период населением одного из микрорайонов города равно 45000 квт 
ч. Оценить вероятность того, что среднемесячное потребление электроэнергии в летний период данного года превзойдёт 120000 квт ч.
5.29. Оценить вероятность того, что отклонение любой случайной величины от её математического ожидания будет не более двух средних квадратических отклонений (по абсолютной величине).
5.30. Производится выборочное обследование большой партии электрических лампочек. Среднее квадратическое отклонение времени горения лампочки равно 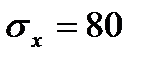ч. Из всей партии наудачу выбирается 400 лампочек. Оценить вероятность того, что среднее время горения лампочки будет отличаться от наблюдаемого среднего времени горения выбранных 400 лампочек не более чем на 10 ч.
5.31. Вероятность появления некоторого события в каждом из 900 независимых испытаний равна 2/5. Воспользовавшись вторым неравенством Чебышёва, оцените вероятность того, что число Х появлений этого события заключено в пределах от 140 до 230.
5.32. Среднее квадратическое изменение курса акции компании в течение одних биржевых торгов составляет 0,2%. Оценить вероятность того, что на ближайших торгах курс изменится более чем на 5%.
5.33. Станок–автомат производит детали высшего качества с вероятностью 0,85. Сколько надо произвести деталей, чтобы с вероятностью 0,95 гарантировать производство 70 деталей высшего качества?
5.34. В среднем за сутки со склада отпускается 19 тонн товара. Оценить вероятность того, что завтра будет отпущено более 35 тонн товара.
6. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
СЛУЧАЙНЫХ ВЕЛИЧИН
6.1. Определение и свойства характеристической функции
Комплексная СВ состоит из двух действительных СВ:
.
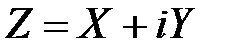При этом
.
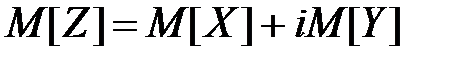Комплексные СВ независимы, если независимы их действительные и мнимые части.