Теорема. Если – независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием m и диcперсией , то при неограниченном увеличении закон распределения их суммы
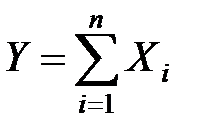
неограниченно приближается к нормальному.
Эта теорема в достаточно широком классе условий справедлива и для неодинаково распределённых слагаемых.
Практически центральной предельной теоремой можно пользоваться и тогда, когда речь идёт о сумме сравнительно небольшого числа (порядка десяти) случайных величин.
В практических задачах часто применяют центральную предельную теорему для вычисления вероятности того, что сумма нескольких случайных величин окажется в заданных пределах.
Пусть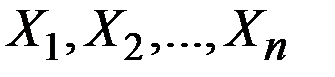 
– независимые случайные величины с математическими ожиданиями 
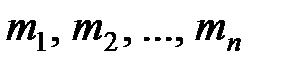и дисперсиями 
.
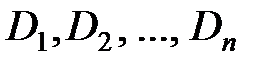Предположим, что условия центральной предельной теоремы выполнены, т.е. величины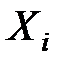 
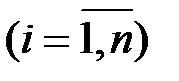сравнимы по порядку своего влияния на рассеивание суммы и число слагаемых n достаточно для того, чтобы закон распределения величины 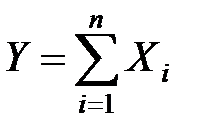можно было считать приближённо нормальным.
Тогда вероятность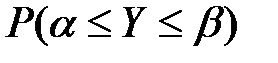 
того, что случайная величина 
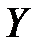попадает в пределы участка 
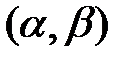, выражается формулой:
,
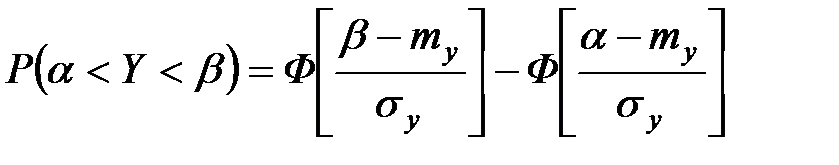где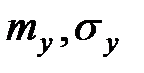 
– математическое ожидание и среднее квадратическое отклонение величины 
;
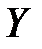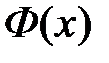– нормальная функция распределения или функция Лапласа.
Согласно теоремам сложения математических ожиданий и дисперсий имеем
;
.
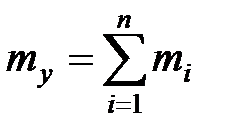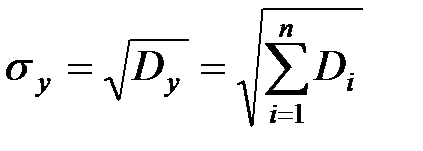Таким образом, для того, чтобы приближённо найти вероятность попадания суммы большого количества случайных величин на заданный участок, не требуется знать законы распределения этих величин, а достаточно знать лишь их характеристики (при выполнении условий центральной предельной теоремы).
Центральная предельная теорема может применяться не только к непрерывным, но и к дискретным случайным величинам при условии, что мы будем оперировать не плотностями, а функциями распределения.
Частным случаем центральной предельной теоремы для дискретных случайных величин является теорема Лапласа: если производится n независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение
,
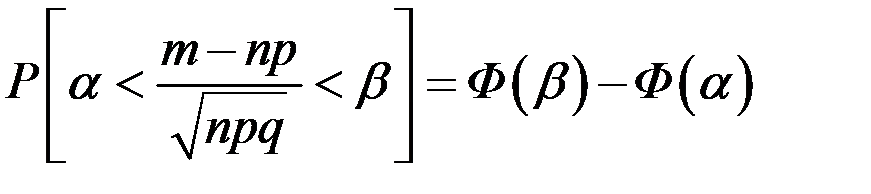где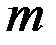 
– число появлений события 
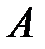в n опытах, 
.
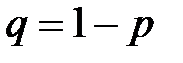На практике эта теорема встречается в двух модификациях.
1. Локальная теорема Лапласа (Муавра–Лапласа).
Если число независимых опытов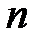 
велико (несколько сотен), то
,
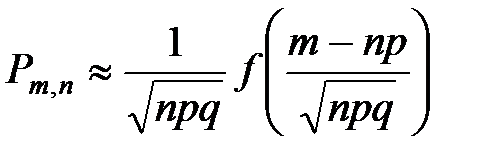где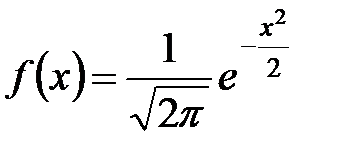 
.
Вероятность того, что событие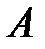 
в n опытах произойдёт ровно m раз, вычисляется через нормированную плотность нормального закона.
Пример 5.6. Станок–автомат требует подналадки в среднем один раз за 4 часа работы. Определить вероятность того, что за 10 суток непрерывной работы подналадка осуществлялась ровно 70 раз.
Решение. Имеем n = 240; m = 70; p = 0,25; q = 0,75.
По локальной теореме Муавра–Лапласа получаем
.
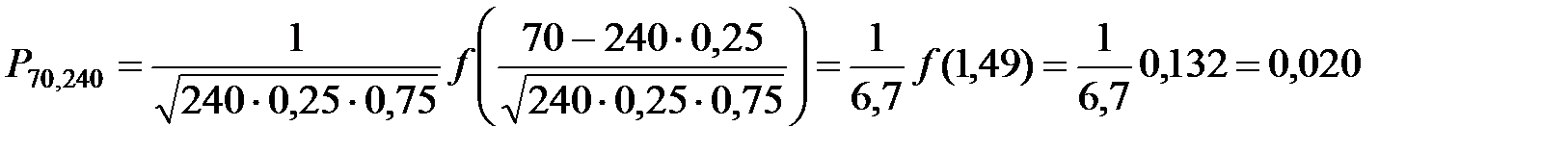По закону Пуассона (параметр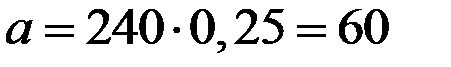 
) эта вероятность составит величину
.
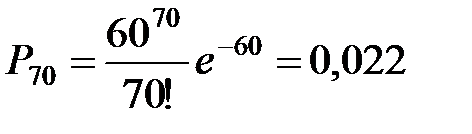Примечание.
Формула Бернулли, локальная теорема Муавра–Лапласа и формула закона Пуассона дают ответ на один и тот же вопрос. Они определяют вероятность того, что в n независимых испытаниях некоторое событие наступит ровно m раз, если в каждом испытании это событие может наступить с постоянной вероятностью р.
По формуле Бернулли получаем точное значение вероятности этого события. Однако из–за вычислительных трудностей эта формула применяется только в случаях, когда число испытаний n невелико.
Если число испытаний будет большим, то используется локальная теорема Муавра–Лапласа, а если, кроме того, вероятность поступления события в отдельном испытании мала, то – формула Пуассона.
Вероятность искомого события, получаемая по локальной теореме Муавра–Лапласа, оказывается достаточно точной, если число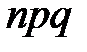 
не меньше 20 
.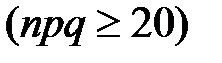