Пример 5.1. Дана случайная величина с математическим ожиданием и дисперсией . Оценить сверху вероятность того, что величина отклонится от своего математического ожидания не меньше, чем на .
Решение. Полагая во втором неравенстве Чебышёва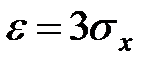 
, получим
,
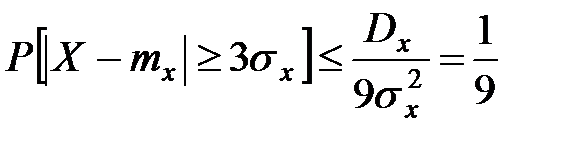т.е. вероятность того, что отклонение случайной величины от её математического ожидания выйдет за пределы трёх средних квадратических отклонений, не может быть больше 1/9 ни при каком законе распределения.
Замечание. На практике в большинстве случаев вероятность того, что величина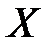 
выйдет за пределы участка 
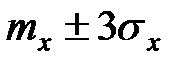, значительно меньше 1/9. Например, для нормального закона эта вероятность приблизительно равна 0,003.
Пример 5.2. В среднем за сутки отпускается со склада 16 тонн различных товаров. Оценить вероятность того, что сегодня будет отпущено не менее 40 тонн.
Решение. По первой форме неравенства Чебышёва находим
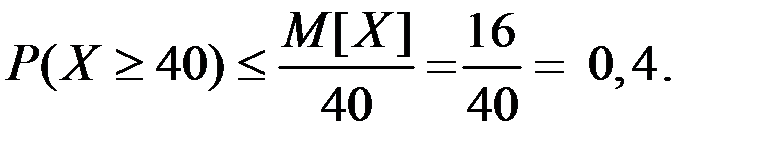
Пример 5.3. Средняя месячная заработная плата в фирме составляет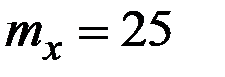 
тыс. руб. Среднее квадратическое отклонение зарплаты 
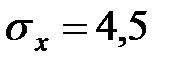тыс. руб. В каких границах находится зарплата у 90% работников фирмы?
Решение. Пусть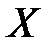 
– месячная заработная плата в фирме.
Тогда по второму неравенству Чебышёва имеем
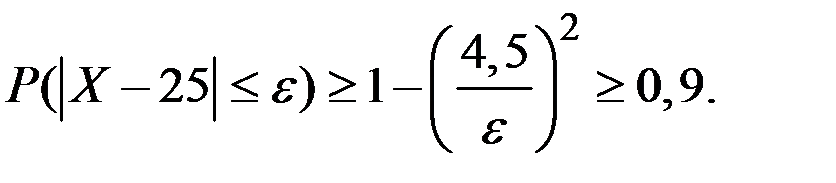
Из этого неравенства находим допустимое отклонение e:
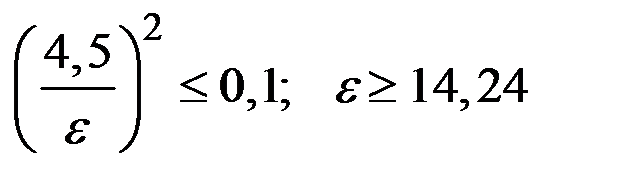тыс. руб.
Следовательно, с вероятностью, не меньшей 0,9, имеем границы зарплаты у 90% работников фирмы:
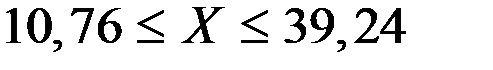тыс. руб.
5.1.2. Теорема Чебышёва (закон больших чисел).
Если последовательность попарно независимых случайных величин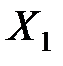 
, 
,..., 
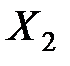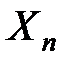имеет конечные математические ожидания и дисперсии этих величин равномерно ограничены (не превышают некоторого постоянного числа 
: 
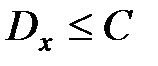), то среднее арифметическое случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий, т.е., если e – любое положительное число, то
.
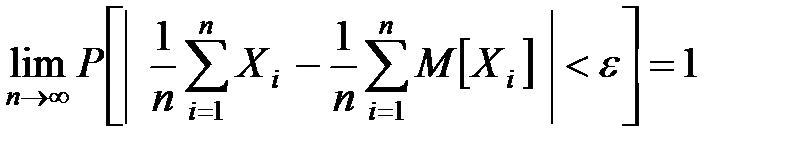5.1.3. Теорема Хинчина (как частный случай) возникает из теоремы Чебышёва при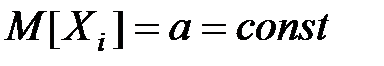 
:
.
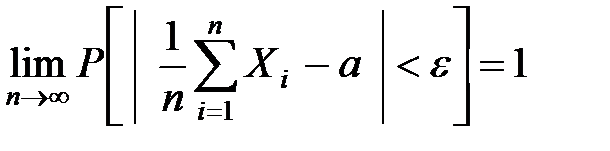В другом виде эту теорему можно записать:
.
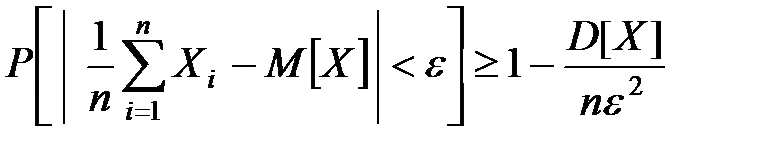5.1.4. Обобщение закона больших чисел (теоремы Чебышёва) на случай зависимых случайных величин принадлежит А.А. Маркову.
Теорема Маркова. Если имеются зависимые случайные величины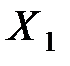 
, 
,..., 
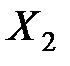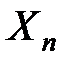, и если при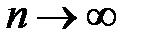 
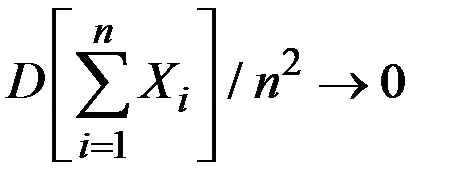, то среднее арифметическое наблюдаемых значений случайных величин 
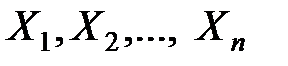сходится по вероятности к среднему арифметическому их математических ожиданий.
5.1.5. Следствием закона больших чисел являются теоремы Бернулли и Пуассона.
Теорема Я. Бернулли утверждает, что при неограниченном увеличении числа опытов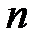 
частота события 
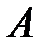сходится к его вероятности:
,
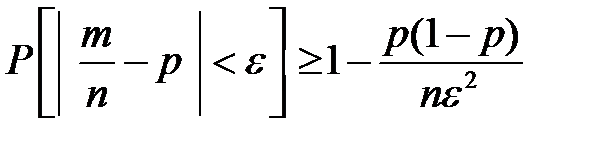где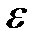 
– сколь угодно малое положительное число,
m – количество наступлений события А.
Теорема Бернулли утверждает устойчивость частоты при постоянных условиях опыта. Но и при изменяющихся условиях опыта аналогичная устойчивость также существует.
Теорема Пуассона устанавливает свойство устойчивости частот при переменных условиях опыта и формулируется следующим образом.
Если производится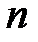 
независимых опытов и вероятность появления события 
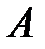в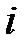 
–м опыте равна 
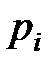, то при увеличении 
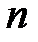частота события 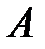сходится по вероятности к среднему арифметическому вероятностей 
.
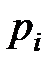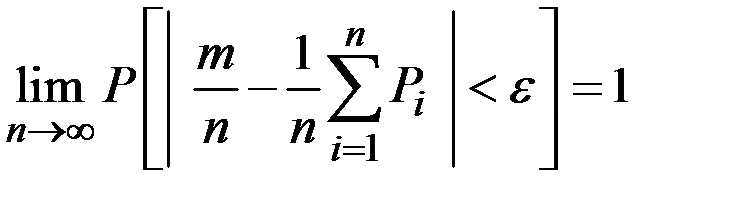
Пример 5.4. Вероятность того, что дилер, торгующий ценными бумагами, продаёт их, равна 0,6. При каком числе ценных бумаг вероятность отклонения доли проданных среди них отклонится от 0,6 не более чем на 0,3 (по абсолютной величине) превысит 0,94?
Решение. Имеем исходные данные
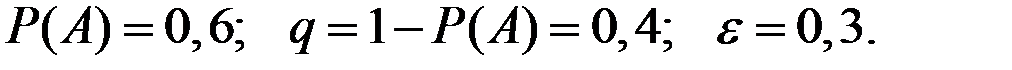
Тогда по теореме Бернулли получаем
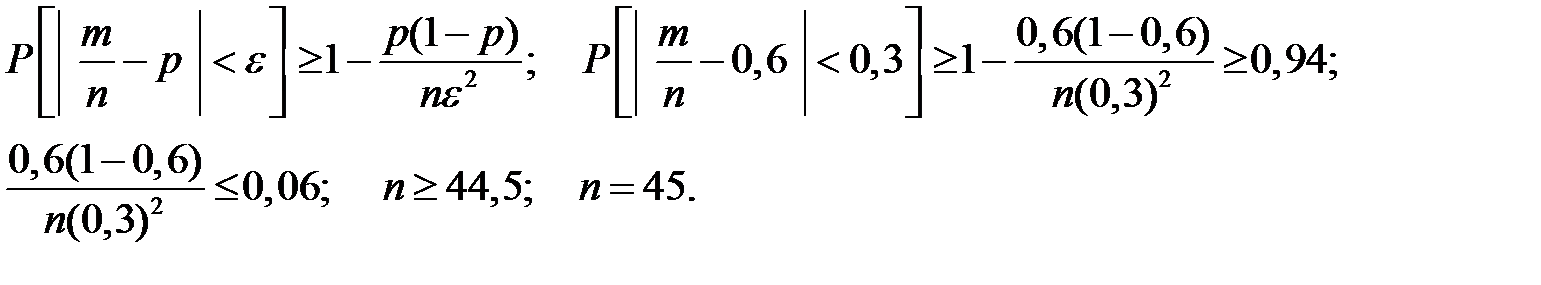
Пример 5.5. Средняя величина вклада в сбербанке составляет 15000 руб. Определить вероятность того, что случайно выбранный вклад не превышает 120000 руб.
Решение. По первому неравенству Чебышёва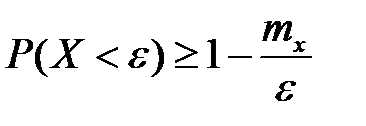 
получим нижнюю оценку искомой вероятности:
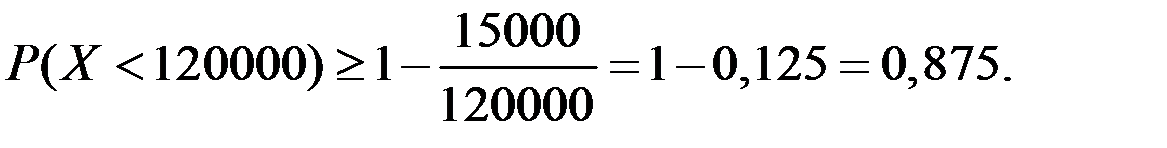
5.2. Центральная предельная теорема
Все формы закона больших чисел утверждают одно: факт сходимости по вероятности тех или иных случайных величин к определённым постоянным. Ни в одной из форм закона больших чисел мы не имеем дела с законами распределения случайных величин.
Все формы центральной предельной теоремы (предельных законов распределения) посвящены установлению условий, при которых возникает нормальный закон распределения.
Различные формы центральной предельной теоремы отличаются между собой условиями, накладываемыми на распределения образующих сумму случайных слагаемых.
Одна из самых простых форм относится к случаю одинаково распределённых слагаемых.