5. Предельные теоремы теории вероятностей
5.1. Закон больших чисел
Свойство устойчивости массовых случайных явлений сводится к следующему. Конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате массы таких явлений. Случайные отклонения от среднего, неизбежные в каждом отдельном явлении, в большой массе явлений взаимно погашаются, нивелируются, выравниваются.
Физическое содержание "закона больших чисел", понимаемого в широком смысле слова, заключается в следующем. При очень большом числе случайных явлений средний их результат практически перестаёт быть случайным и может быть предсказан с большой степенью определённости.
В узком смысле слова под "законом больших чисел" понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к некоторым определённым постоянным.
Различные формы "закона больших чисел" (теоремы Бернулли, Чебышёва, Маркова и др.) вместе с различными формами центральной предельной теоремы (группа теорем, касающихся уже не предельных значений случайных величин, а предельных законов распределения) образуют совокупность так называемых предельных теорем теории вероятностей.
Предельные теоремы дают возможность не только осуществлять научные прогнозы в области случайных явлений, но и оценивать точность этих прогнозов.
5.1.1. Неравенства Чебышёва.
Первая форма (первое неравенство Чебышёва): если СВ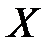 
неотрицательна ( 
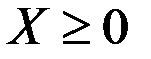) и имеет математическое ожидание, то
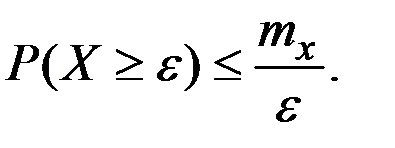
В другом виде это неравенство можно записатьтак:
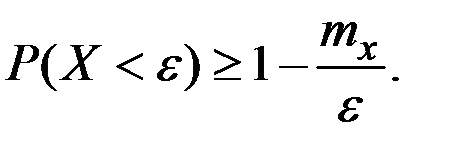
Вторая форма: (второе неравенство Чебышёва): если дисперсия случайной величины Х ограничена (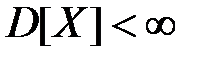 
), то вероятность того, что отклонение величины Х от её математического ожидания по абсолютной величине на значение, меньшее положительного числа e, не меньше, чем 
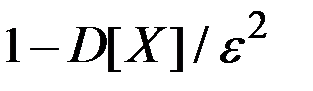, т.е.
;
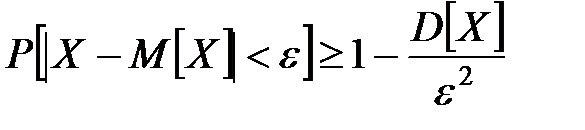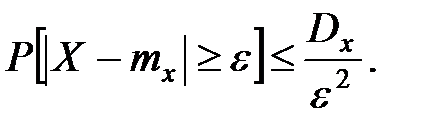
Неравенства Чебышёва дают только верхнюю границу вероятности рассматриваемого отклонения, выше этой границы вероятность не может быть ни при каком законе распределения.
Наиболее часто используется вторая форма неравенства.