4.2. Известно, что . Найти закон распределения Y.
4.3. На окружности радиуса 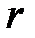 случайным образом располагаются две точки, которые затем соединяются между собой и с центром окружности. Найти математическое ожидание площади полученного треугольника.
случайным образом располагаются две точки, которые затем соединяются между собой и с центром окружности. Найти математическое ожидание площади полученного треугольника.
4.4. Пусть X, Y, Z – случайные величины: X – выручка фирмы, Y – её затраты, Z = X – Y – прибыль.
| X: | 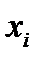
| 3 | 4 | 5 | Y: | 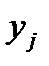
| 1 | 2 | |
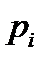
| 1/3 | 1/3 | 1/3 | 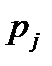
| 1/2 | 1/2 |
Найти распределения прибыли Z .
4.5. Вес гайки и болта являются нормально распределёнными величинами с математическими ожиданиями 15 и 40 гр. и средними квадратическими отклонениями 2 и 5 гр., соответственно. Ковариационный момент этих величин равен 7 гр.2. Найти среднее квадратическое отклонение веса всего узла «гайка + болт».
4.6. Дискретные независимые СВ заданы своими распределениями:
| X | 2 | 3 | Y | 4 | 5 |
| P | 0,3 | 0,7 | P | 0,6 | 0,4 |
Найти коэффициент вариации величины Z = X + Y.
4.7. Независимые СВ X и Y заданы плотностью распределения:
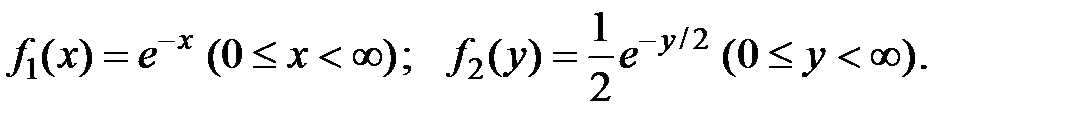
Найти плотность распределения СВ Z = X + Y.
4.8. Ошибка прибора выражается функцией 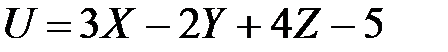 , где
, где  – так называемые первичные ошибки, представляющие собой систему случайных величин, которая характеризуется математическими ожиданиями
– так называемые первичные ошибки, представляющие собой систему случайных величин, которая характеризуется математическими ожиданиями 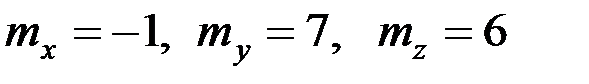 и корреляционной матрицей
и корреляционной матрицей 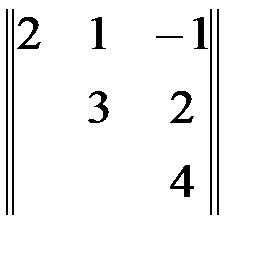 . Найти среднее квадратическое отклонение ошибки прибора.
. Найти среднее квадратическое отклонение ошибки прибора.
4.9. Дискретная случайная величина  имеет ряд распределения, представленный в таблице.
имеет ряд распределения, представленный в таблице.
| 1 | 2 | 3 | 4 |
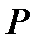
| 0,1 | 0,4 | 0,3 | 0,2 |
Найдите математическое ожидание и дисперсию величины 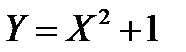 .
.
4.10. Связь между нормально распределёнными показателями Х и Y выражается зависимостью Y = 1,3х + 0,5. При этом дисперсия Y в 4 раза выше дисперсии Х. Найти степень тесноты связи величин Х и Y.
4.11. Показатель Y выражается формулой 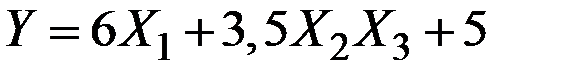 , где
, где 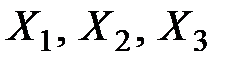 представляют собой величины с математическими ожиданиями
представляют собой величины с математическими ожиданиями 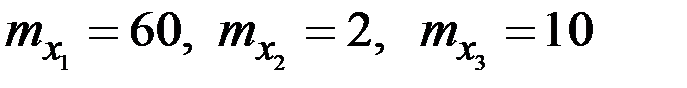 и средними квадратическими отклонениями
и средними квадратическими отклонениями 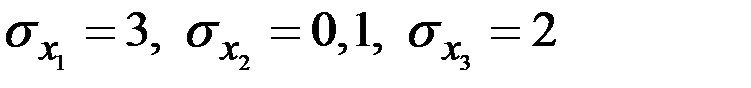 Нормированная корреляционная матрица системы имеет вид:
Нормированная корреляционная матрица системы имеет вид: 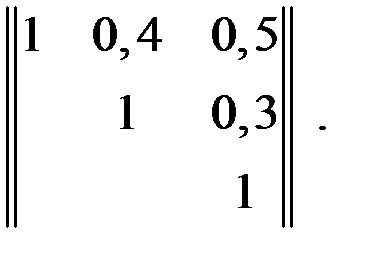 Найти среднее квадратич. отклонение СВ Y.
Найти среднее квадратич. отклонение СВ Y.
4.12. Случайные величины 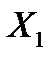 и
и 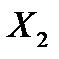 имеют математические ожидания
имеют математические ожидания 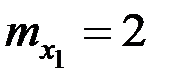 ,
, 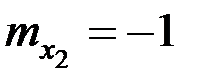 , дисперсия
, дисперсия 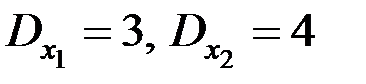 и ковариацию
и ковариацию 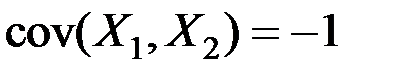 . Найдите математическое ожидание и дисперсию случайной величины
. Найдите математическое ожидание и дисперсию случайной величины
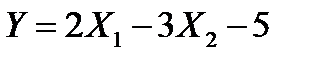 .
.
4.13. Независимые случайные величины 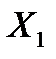 и
и 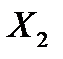 имеют экспоненциальное распределение с параметрами
имеют экспоненциальное распределение с параметрами 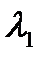 и
и 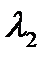 соответственно. Найти математическое ожидание случайной величины
соответственно. Найти математическое ожидание случайной величины 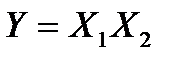 .
.
4.14. Два стрелка независимо один от другого производят по одному выстрелу в мишень. Вероятность попадания для каждого из стрелков равна 0,6. Пусть случайные величины X и Y означают число попаданий в мишень для первого и для второго стрелка соответственно. Построить закон распределения и найти математическое ожидание для случайной величины 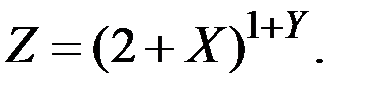
4.15. СВ X задана плотностью распределения f(x) = (1/2)sin(x) в интервале (0,p); вне интервала f(x) = 0. Найти дисперсию величины Y=X2.
4.16. Случайная величина X задана плотностью вероятности 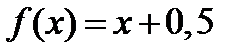 в интервале (0;1); вне этого интервала
в интервале (0;1); вне этого интервала 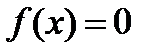 . Найти математическое ожидание функции
. Найти математическое ожидание функции 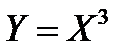 .
.
4.17. Две случайные величины (X и Y) имеют характеристики: 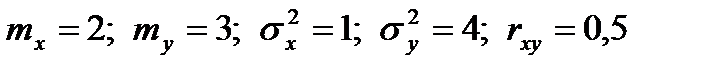 . Определить дисперсию суммы и разности этих величин.
. Определить дисперсию суммы и разности этих величин.
4.18. Две независимые случайные величины (X и Y) распределены равномерно: Х на интервале[- 5; 1], Y на интервале [3; 6]. Найти математическое ожидание и дисперсию случайной величины 7Х - 9Y + 8.
4.19. Ребро куба измерено приближённо, причём 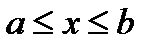 . Рассматривая ребро куба как случайную величину X, распределённую равномерно в интервале (a, b), найти математическое ожидание объёма куба.
. Рассматривая ребро куба как случайную величину X, распределённую равномерно в интервале (a, b), найти математическое ожидание объёма куба.
4.20. Дискретные независимые СВ заданы своими распределениями:
| X | 1 | 3 | Y | 2 | 4 |
| P | 0,3 | 0,7 | P | 0,6 | 0,4 |
Найти коэффициент вариации величины Z = 2X + 3Y.
4.21. Предприятие состоит из двух подразделений. Месячная прибыль каждого подразделения является нормально распределённой величиной с математическими ожиданиями 550 и 400 тыс. руб. и средними квадратическими отклонениями 60 и 50 тыс. руб., соответственно. Ковариационный момент этих величин равен 70 тыс. руб.2 Найти коэффициент вариации прибыли всего предприятия.
4.22. Один станок даёт в среднем 3% брака, другой – 5%. Производительности станков одинаковы. Каков коэффициент вариации числа бракованных изделий в общей продукции из 100 деталей?
4.23. Две СВ (X и Y) имеют характеристики:
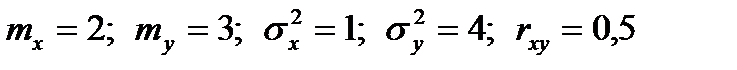 .
.
Определить дисперсию суммы этих величин.
4.24. Вес гайки и болта являются нормально распределёнными величинами с математическими ожиданиями 10 и 40 гр. и средними квадратическими отклонениями 2 и 5 гр., соответственно. Ковариационный момент этих величин равен 7 гр.2. Найти среднее квадратическое отклонение веса всего узла «гайка + болт».
4.25. Погрешность в изготовлении детали образуются в результате суммарного воздействия трёх факторов А, В и С. Их характеристики известны:
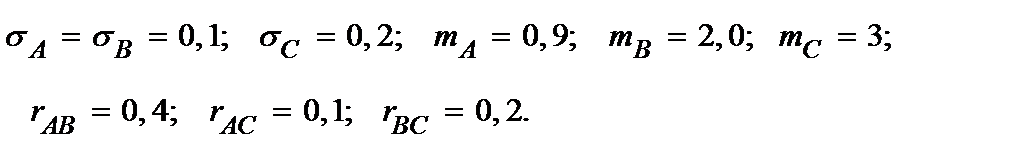
Найти среднее квадратичное отклонение погрешности изготовления детали.
4.26. Даны законы распределения двух независимых СВ Х и Y
| X | 1 | 2 | 3 | Y | – 1 | 1 | 2 | 4 |
| P | 0,3 | 0,6 | 0,1 | P | 0,15 | 0,25 | 0,2 | 0,4 |
Найти характеристики М(ХY – 5Х + 2Y – 7), D(8Х – 3Y + 4).
4.27. Независимые СВ X и Y заданы плотностью распределения:
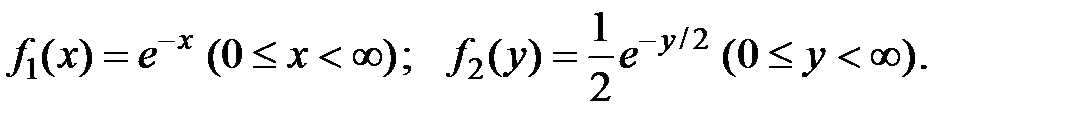
Найти плотность распределения СВ Z = X + Y.
4.28. Время настройки прибора подчинено показательному распределению со средним значением 3 минуты. Чему среднее значение квадрата времени настройки прибора?
4.29. Размеры квадратного листа фанеры равномерно распределены в интервале от 31 до 33 сантиметров. Найти среднюю площадь листа.
4.30. Вероятность брака деталей, производимых станком–автоматом, равна 0,025. Найти математическое ожидание квадрата числа бракованных деталей в ящике из 200 деталей.
4.31. Сопротивление каждого из двух последовательно соединённых резисторов распределено равномерно в диапазоне 100 – 120 ом. Найти функцию распределения сопротивления всей цепи и вероятность того, что это сопротивление превысит 210 ом.








