Если система случайных величин распределена по нормальному закону, но величины X и зависимы, то закон распределения величины также является нормальным.
Центры рассеивания складываются алгебраически, но для средних квадратичных отклонений правило становится более сложным:
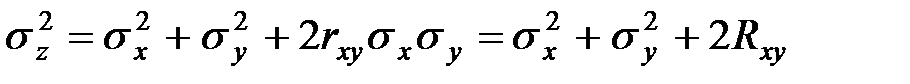 ,
,
где 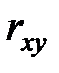 – коэффициент корреляции величин
– коэффициент корреляции величин 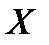 и
и 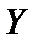 .
.
Если 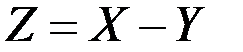 , то
, то 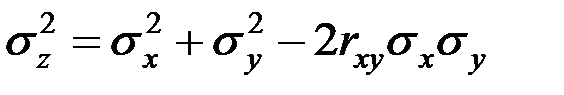 .
.
При сложении нескольких зависимых случайных величин, подчинённых в своей совокупности нормальному закону, закон распределения их суммы 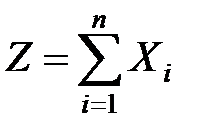 , также оказывается нормальным с параметрами
, также оказывается нормальным с параметрами
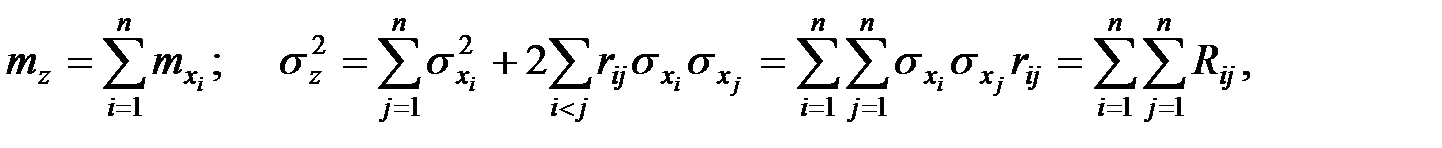
где 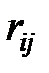 – коэффициент корреляции величин
– коэффициент корреляции величин 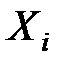 и
и 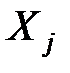 , а суммирование распространяется на все различные попарные комбинации величин
, а суммирование распространяется на все различные попарные комбинации величин 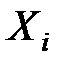 .
.
Свойством устойчивости обладают весьма немногие законы распределения. Например, закон равномерной плотности неустойчив: при композиции двух законов равномерной плотности получается закон Симпсона. Устойчивостью обладает и закон Пуассона.
Пример 4.11. Имеются две независимые случайные величины (X,Y). СВ Х имеет показательное распределение со средним значением 0,5. СВ Y имеет равномерное распределение для значений 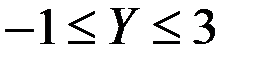 . Найти математическое ожидание, дисперсию и закон распределения их суммы.
. Найти математическое ожидание, дисперсию и закон распределения их суммы.
Решение. Имеем характеристики для СВ Х:
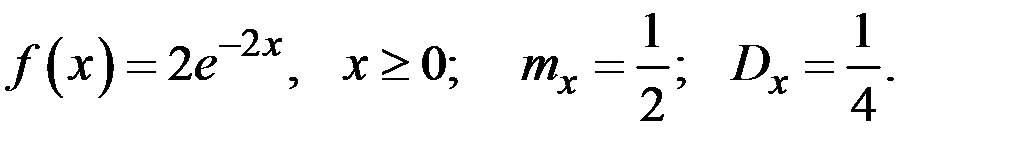
Имеем характеристики для СВ Y:
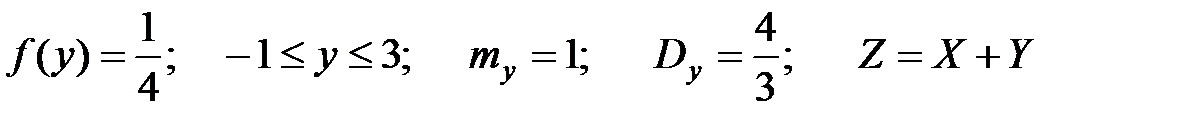 .
.
Используем композицию законов распределения
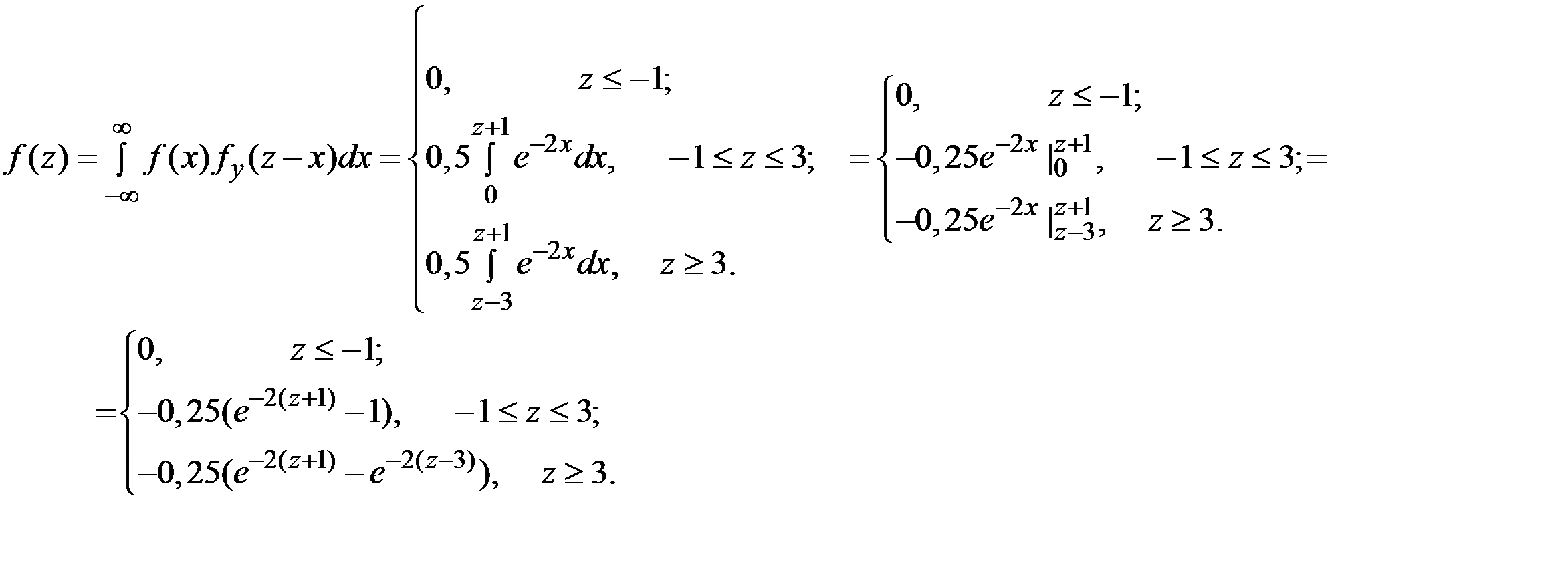
Окончательно имеем:
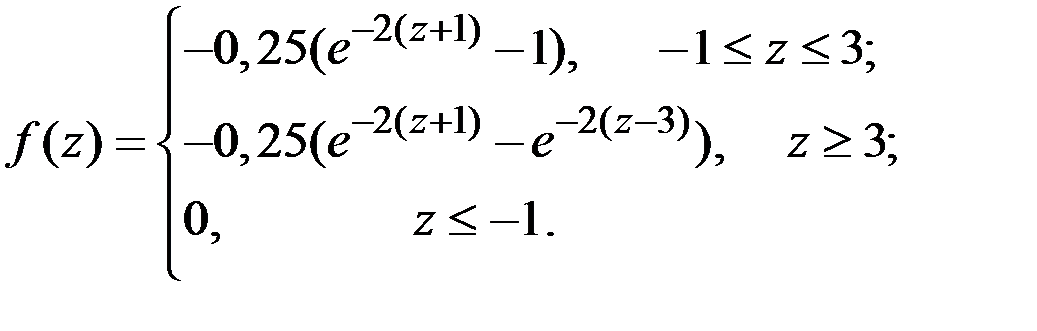
Математическое ожидание и дисперсия величины 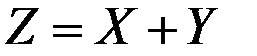 соответственно равны значениям:
соответственно равны значениям:
Пример 4.12. Найти закон распределения суммы двух независимых равномерно распределённых на отрезке [a, b] случайных величин.
Решение. Используем правило композиции двух законов распределения.
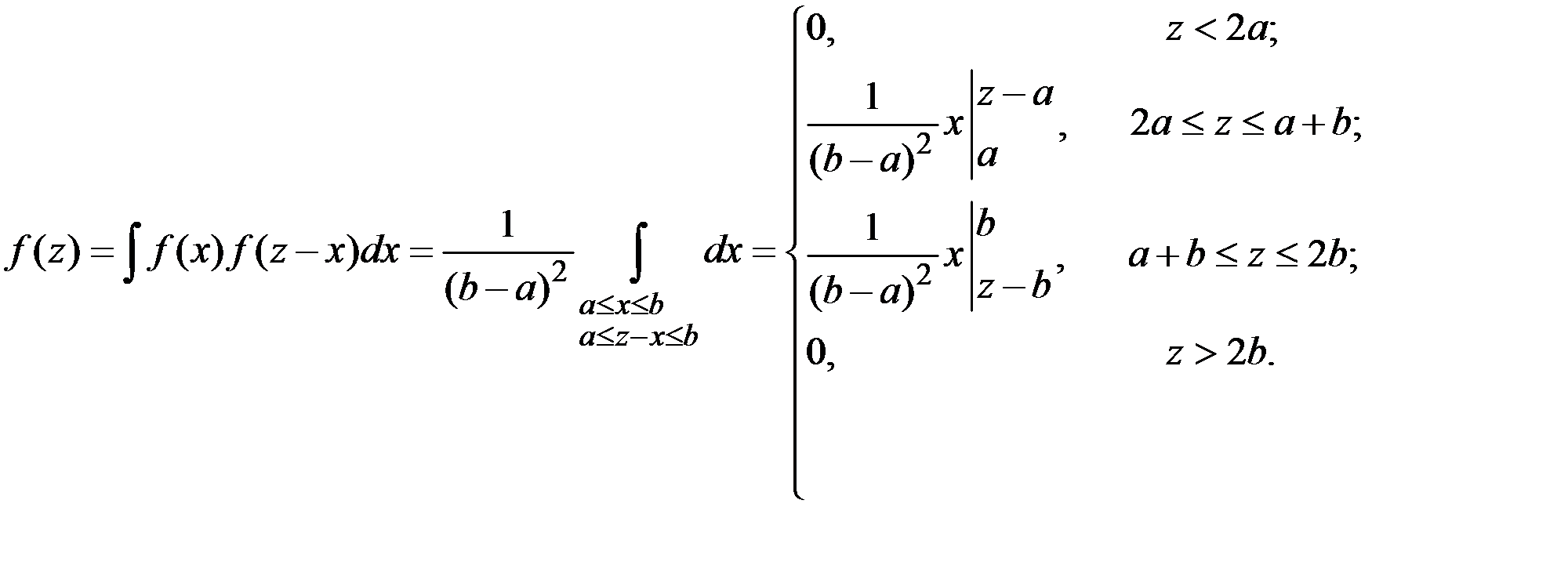 Окончательно получаем:
Окончательно получаем:
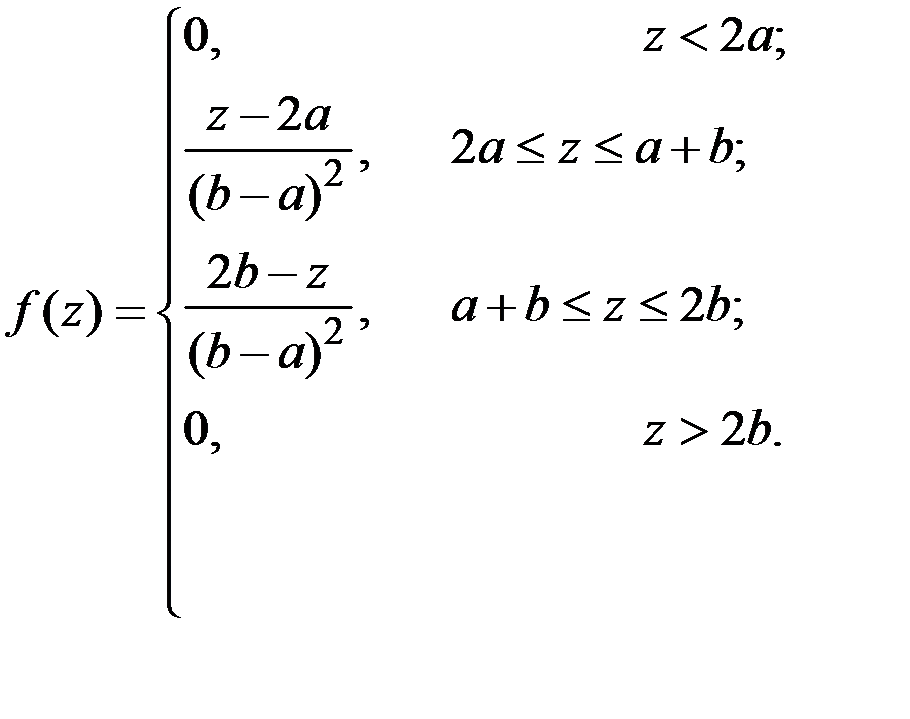
Получили треугольное распределение с вершиной в точке
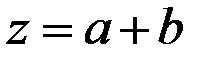 .
.
Функция плонности в этой точке
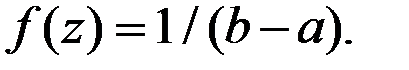
4.4. Решение типовых задач главы 4
Пример 4.13. Случайные величины 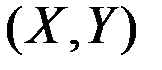 имеют характеристики
имеют характеристики 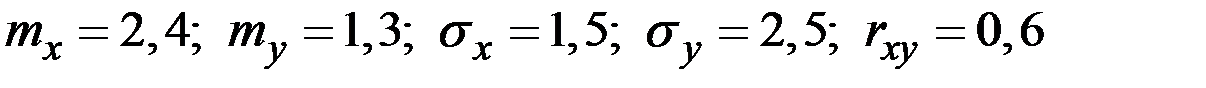 . Вычислить дисперсию разности величин
. Вычислить дисперсию разности величин 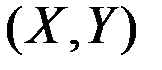 .
.
Решение. Дисперсия разности величин 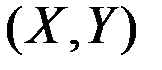 вычисляется по соотношению:
вычисляется по соотношению:
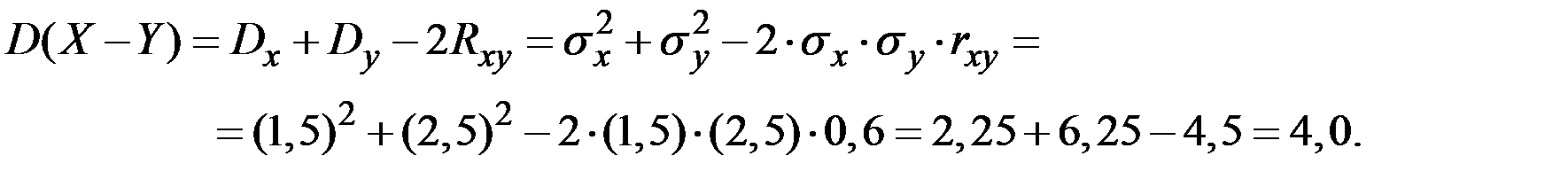
Пример 4.14. Найти распределение куба нормальной СВ с нулевым математическим ожиданием.
Решение.
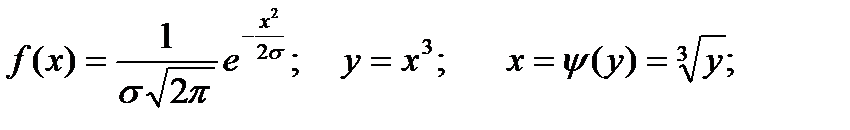
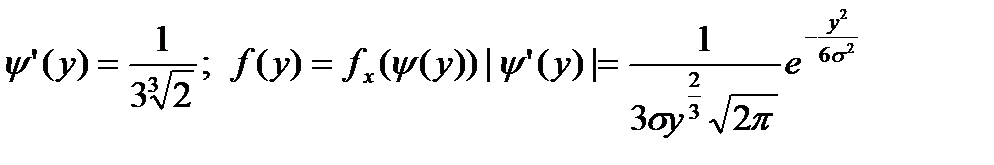
Пример 4.15. Размеры прямоугольного листа бумаги равномерно распределены в интервалах [10; 12] и [19; 21] сантиметров. Коэффициент корреляции между размерами равен 0,8. Найти среднюю площадь листа.
Решение. Математическое ожидание произведения двух величин определяется соотношением
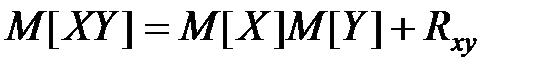 . Имеем:
. Имеем:
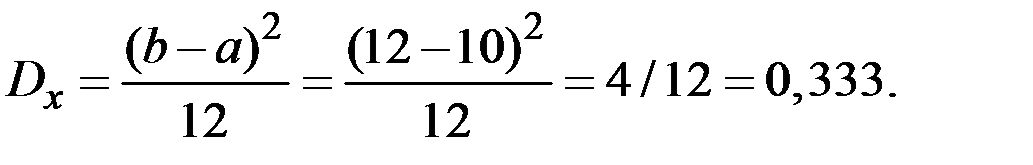
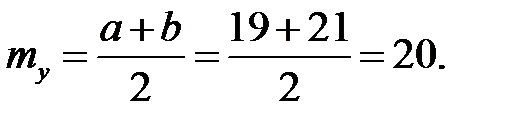
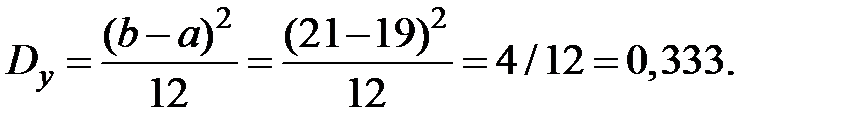
Тогда
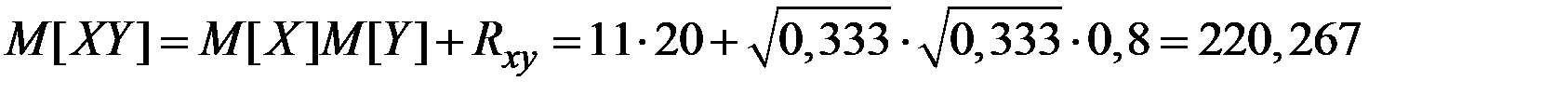 (см.)2.
(см.)2.
Пример 4.16. Две независимые случайные величины Х и У распределены равномерно: величина Х на интервале [– 4; 1], величина У на интервале [3; 5]. Найти математическое ожидание случайной величины Z = 6Х - 3У + 5.
Решение. Имеем дисперсии величин из свойств равномерного закона:
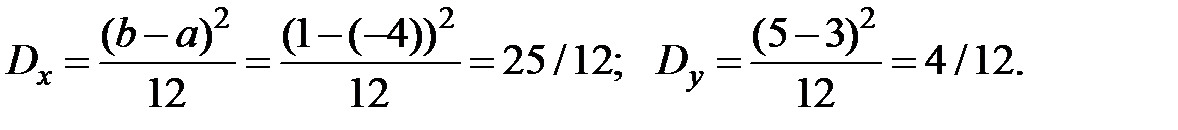
Тогда дисперсия случайной величины Z:
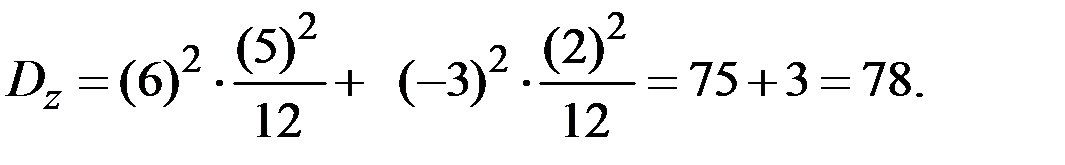
Пример 4.17. Время настройки прибора подчинено показательному распределению со средним значением 3 минуты. Чему среднее значение квадрата времени настройки прибора?
Решение. Имеем закон распределения времени настройки  прибора в виде
прибора в виде
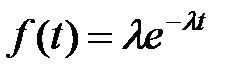 , где
, где 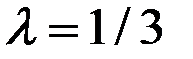 .
.
У показательного распределения
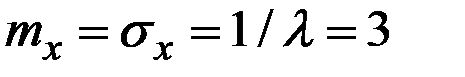 минуты.
минуты.
Дисперсия величины Х:
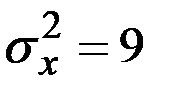 (мин.)2.
(мин.)2.
Среднее значение квадрата времени настройки прибора:
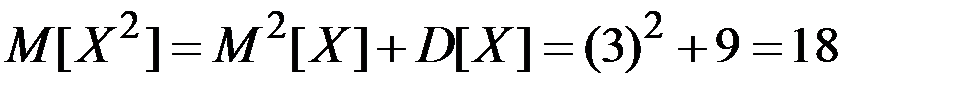 (мин.)2.
(мин.)2.
Пример 4.18. Погрешность в изготовлении детали образуется в результате суммарного воздействия трёх факторов А, В, С.
Их характеристики известны:
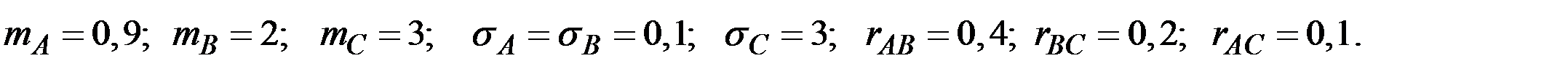
Найти дисперсию отклонение погрешности изготавливаемых детали.
Решение. Имеем характеристики трёх СВ:
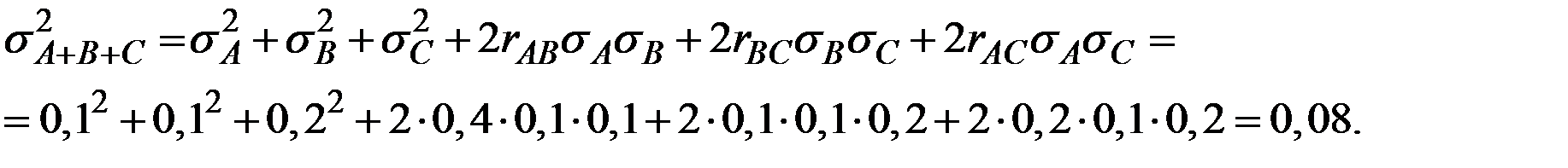
Пример 4.19. Найти коэффициент корреляции r(X, X + Y), где X и Y независимы и распределены по стандартному нормальному закону.
Решение.
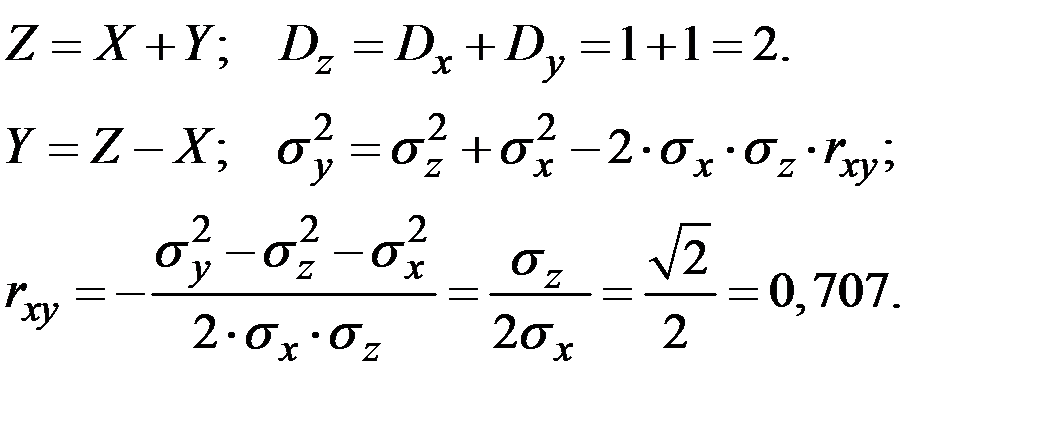
Пример 4.20. Случайные величины 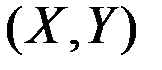 независимы и имеют характеристики
независимы и имеют характеристики 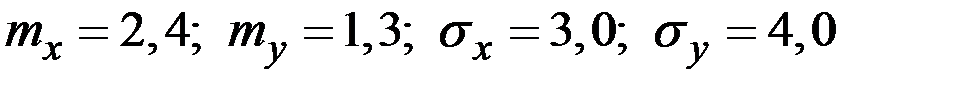 .
. 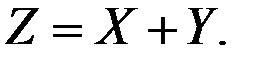 Вычислить дисперсию величины
Вычислить дисперсию величины 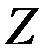 и все парные коэффициенты корреляции.
и все парные коэффициенты корреляции.
Решение. В силу независимости величин 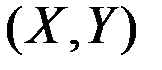 их коэффициент корреляции равен нулю:
их коэффициент корреляции равен нулю: 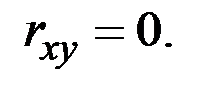
Дисперсию величины  вычисляется по соотношению:
вычисляется по соотношению:
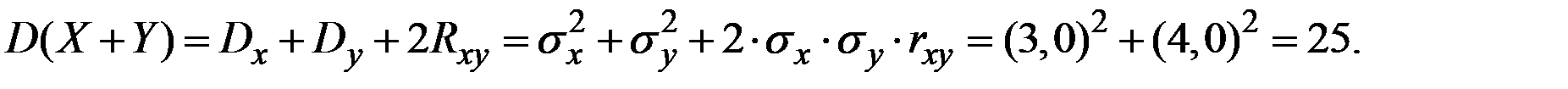
Для случайной величины 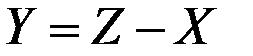 имеем соотношение
имеем соотношение
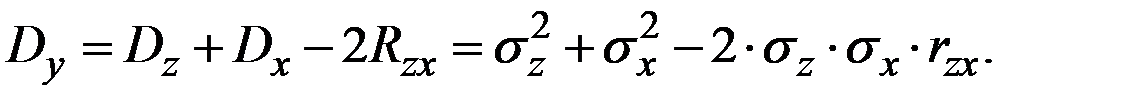
Отсюда:
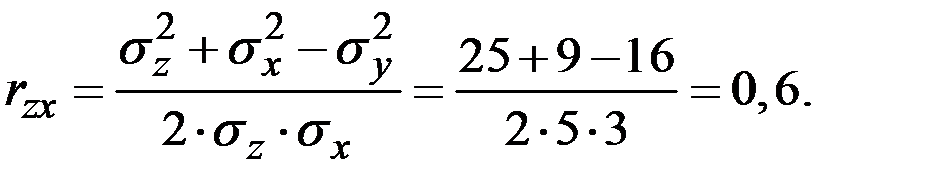
Аналогично 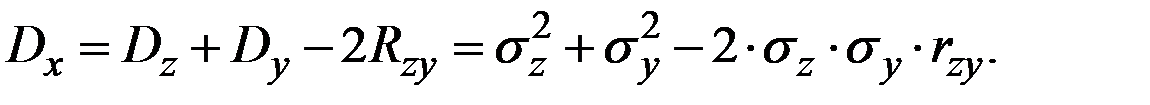
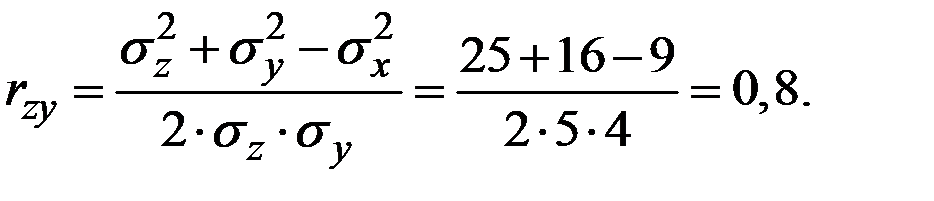
Пример 4.21. Величина Х имеет характеристики 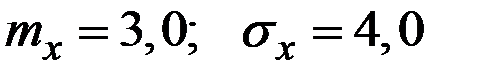 . Величина Y = 4+6 Х. Вычислить характеристики
. Величина Y = 4+6 Х. Вычислить характеристики 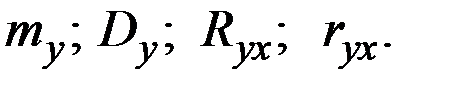
Решение.
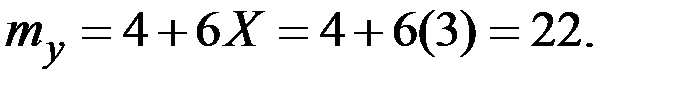
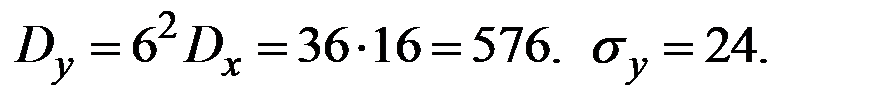
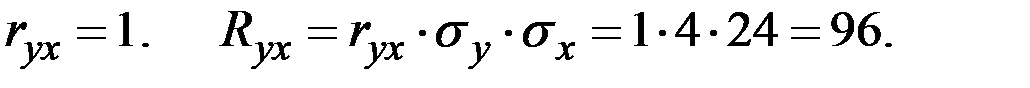
Пример 4.22. Величина Х имеет характеристики 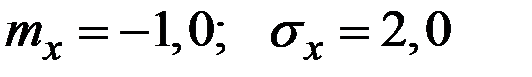 . Величина Y = 2 – 3 Х. Вычислить характеристики
. Величина Y = 2 – 3 Х. Вычислить характеристики 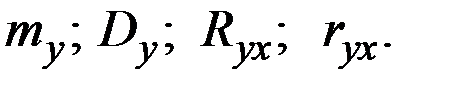
Решение.
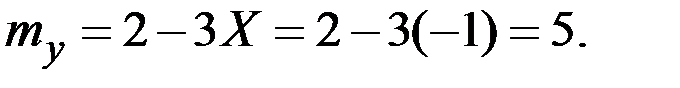
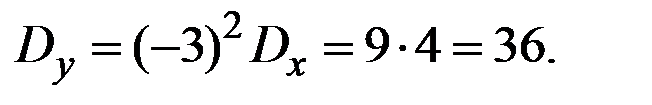
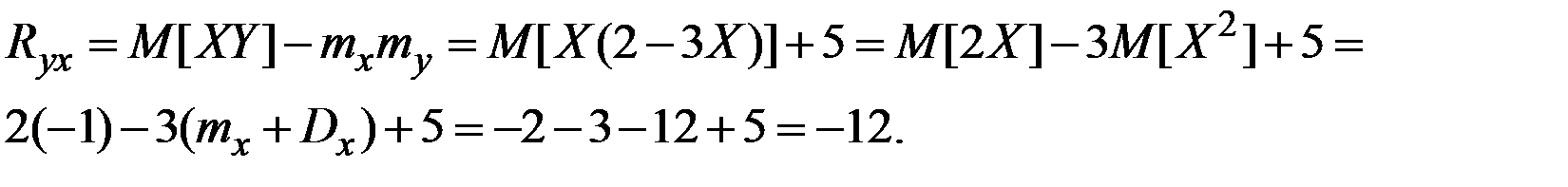
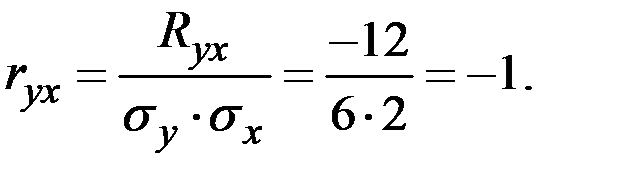
Пример 4.23. Величина Х имеет характеристики 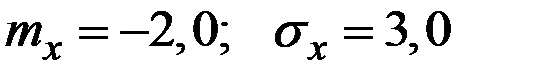 . Величина Y = 3 – 5 Х. Вычислить характеристики
. Величина Y = 3 – 5 Х. Вычислить характеристики 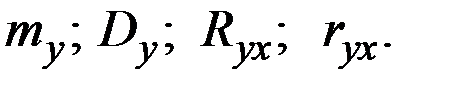
Решение.
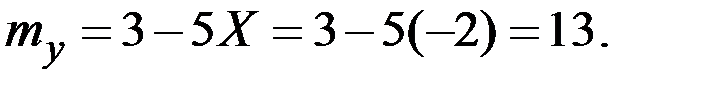
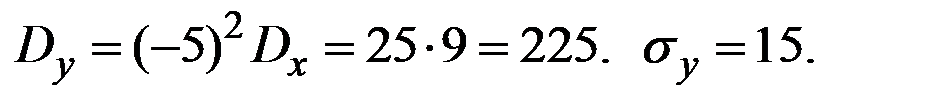
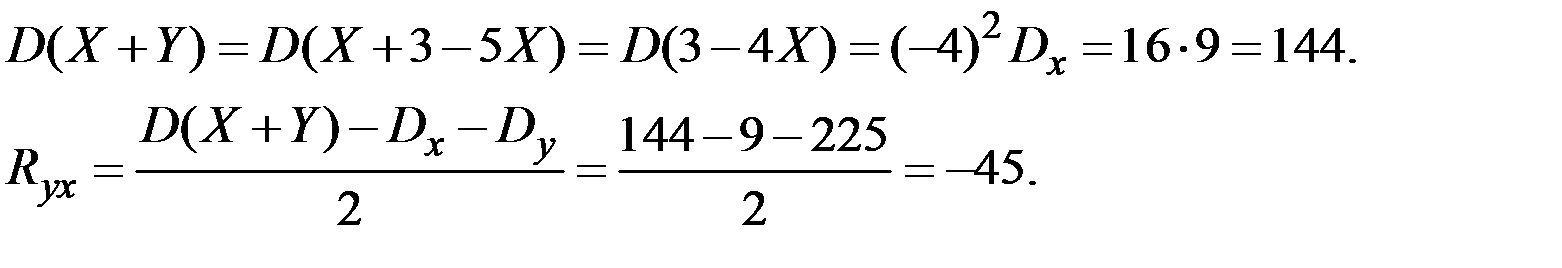
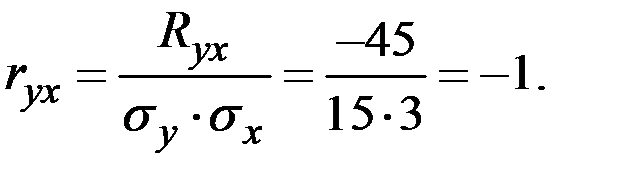
Пример 4.24. Величины X и Y независимы и имеют одинаковое распределение с математическим ожиданием m и дисперсией σ2. Найти коэффициент корреляции случайных величин U = aX + bY и V = aX – bY .
Решение. Имеем
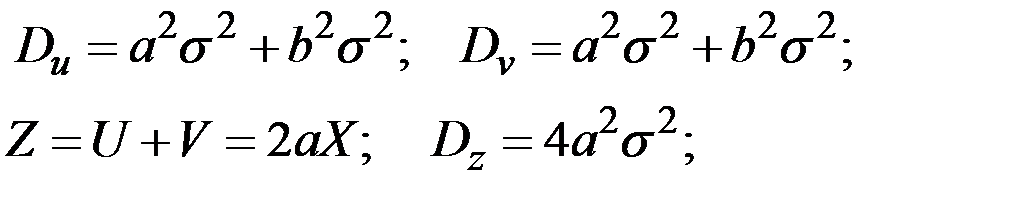
С другой стороны
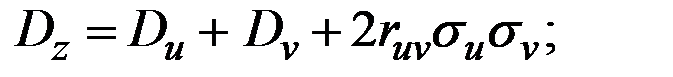
Отсюда:
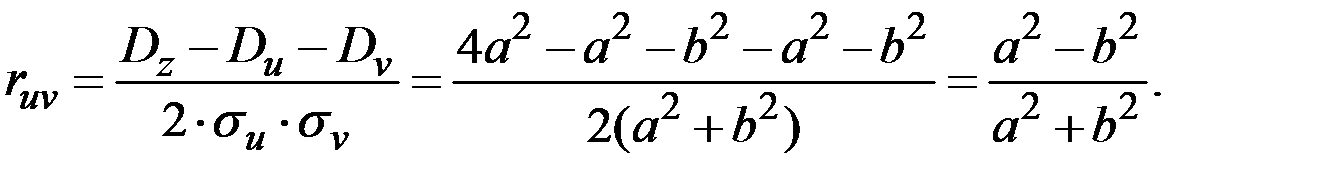
Пример 4.25. Пусть X – непрерывная случайная величина с плотностью распределения:
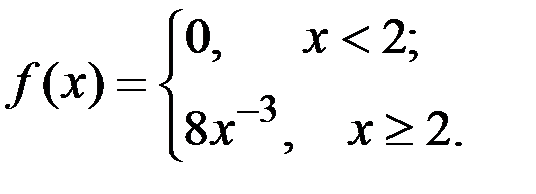
Найти функцию плотности распределения для случайной величины
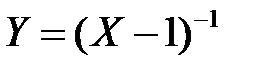 при 0 < y ≤ 1.
при 0 < y ≤ 1.
Решение. Так как обратная функция 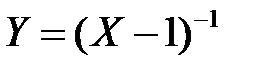 монотонная на участке
монотонная на участке 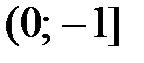 , то
, то
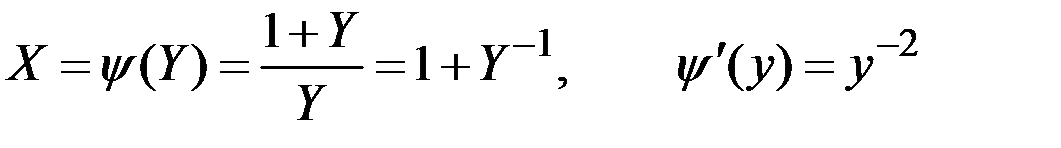 .
.
Следовательно, используем соотношение
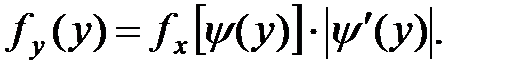
Получаем функцию плотности распределения величины Y:
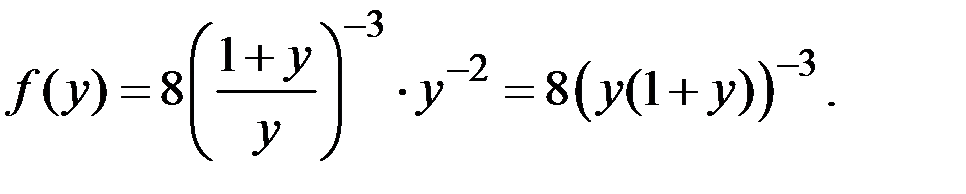
Пример 4.26. Предприятие состоит из двух подразделений. Месячная прибыль каждого подразделения является нормально распределённой величиной с математическими ожиданиями 550 и 400 тыс. руб. и средними квадратическими отклонениями 60 и 50 тыс. руб., соответственно. Ковариационный момент этих величин равен 70 тыс. руб.2 Найти коэффициент вариации прибыли всего предприятия.
Решение. Имеем характеристики двух СВ:
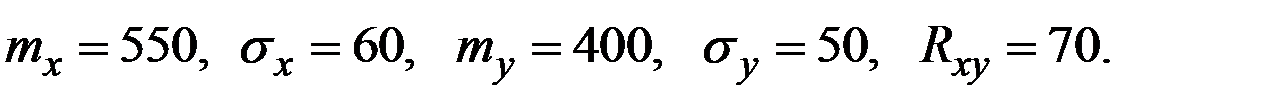
Используем формулу для дисперсии суммы:
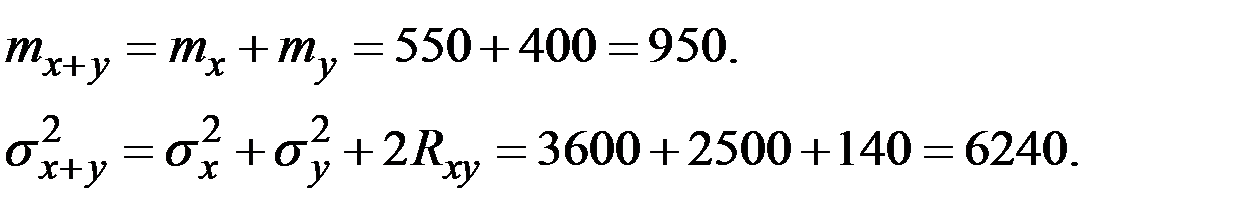
Следовательно
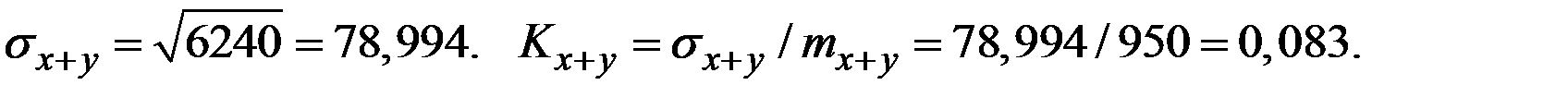
Пример 4.27. Две СВ имеют характеристики
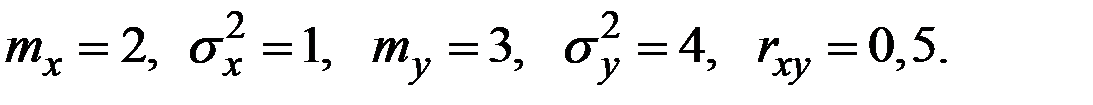
Определить дисперсию суммы этих величин.
Решение. Используем формулу для дисперсии суммы:
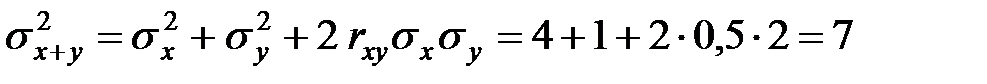 .
.
Контрольные задачи к главе 4
4.1. Из накопителя перед первой технологической операцией детали забираются на обработку регулярно через каждые 10 минут. Из накопителя перед второй технологической операцией детали забираются на обработку регулярно через каждые 30 минут. Найти в процентах коэффициент вариации суммарного времени ожидания детали в накопителях (при случайном её попадании туда).








