То есть, если функция монотонная, для которой обратная функция однозначная, то плотность распределения СВ Y определяется формулой
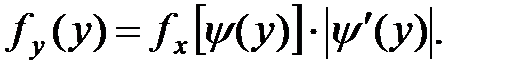
Если на интервале возможных значений X обратная функция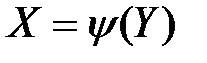 
неоднозначна (рис. 4.2), то есть одному значению y соответствует несколько значений X: 
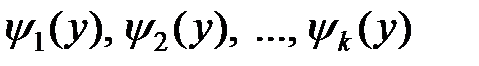, то плотность распределения случайной величины Y определяется формулой
.
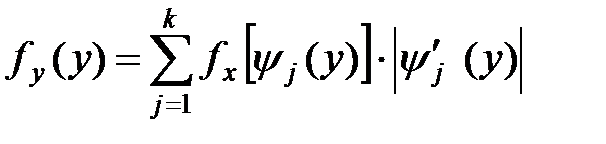Рис. 4.2. Неоднозначная функция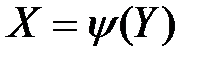 
Для случая двух переменных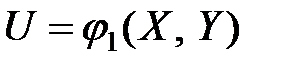 
и 
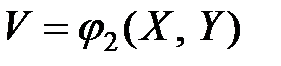аналогично можно получить:
,
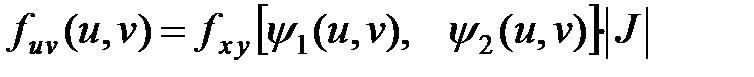где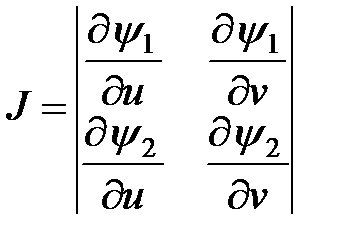 
– Якобиан преобразования.
В общем случае n переменных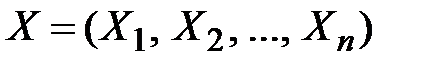 
и преобразований 
, ... , 
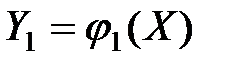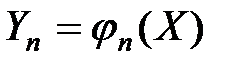плотность вероятности преобразованных величин равна 
.
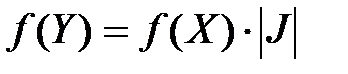Якобиан в этом случае равен: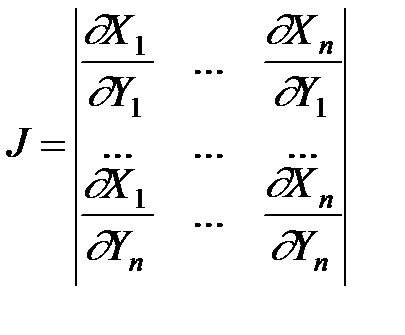 
.
Якобиан существует, конечно, при условии существования и единственности всех частных производных, входящих в него.
Пример 4.1. Случайная величина X подчинена закону Коши с плотностью распределения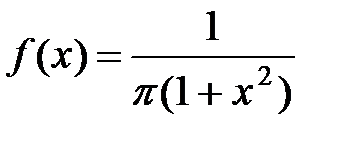 
, величина Y связана с X зависимостью 
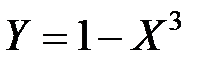. Найти плотность распределения величины Y.
Решение. Так как обратная функция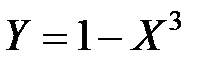 
монотонная на участке 
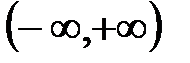, то
.
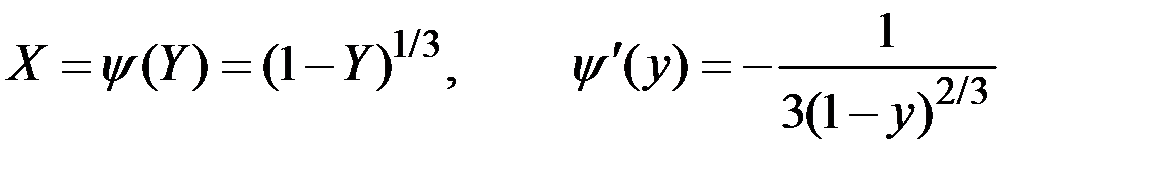Следовательно
.
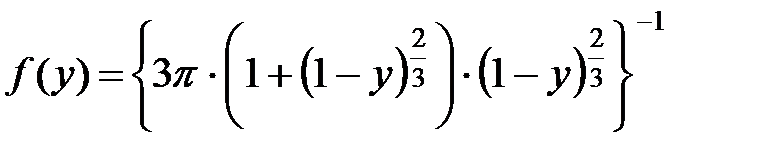Пример 4.2. Найти распределение куба нормальной СВ с нулевым математическим ожиданием.
Решение.
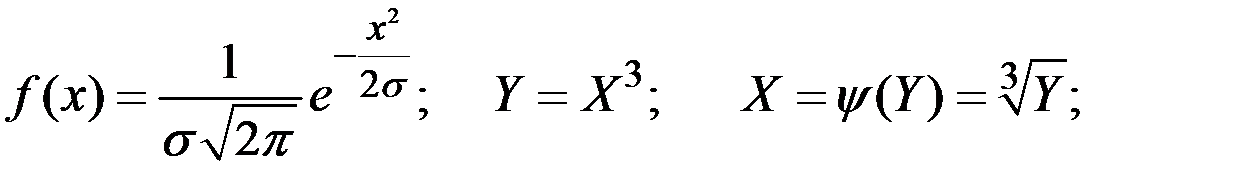
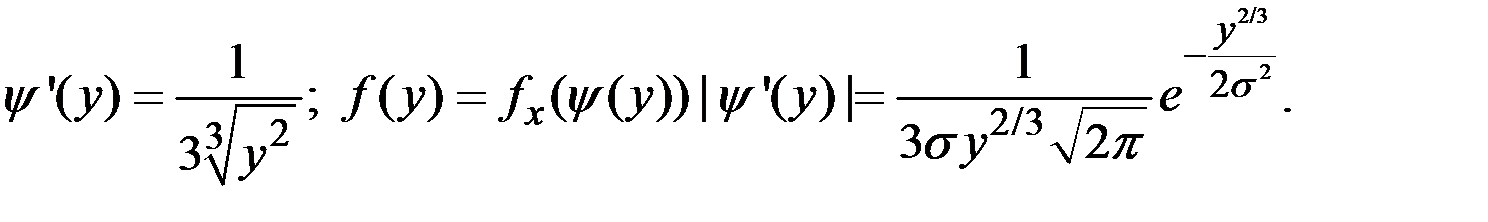
Пример 4.3. Случайная величина X подчинена закону с плотностью распределения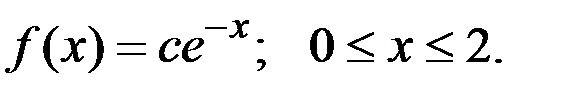 
Величина Y связана с X зависимостью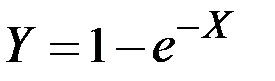 
.
Найти плотность распределения величины Y.
Решение. Найдём параметр 
из условия нормировки, а затем найдём плотность распределения величины Y . Получаем:
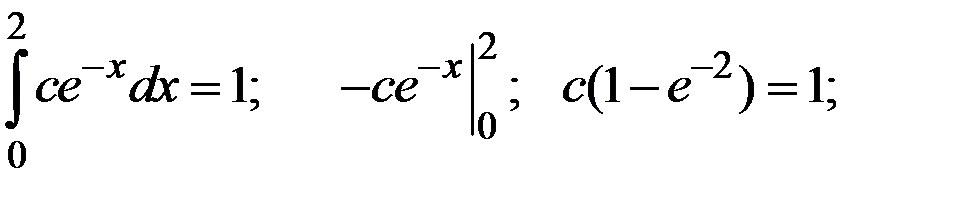
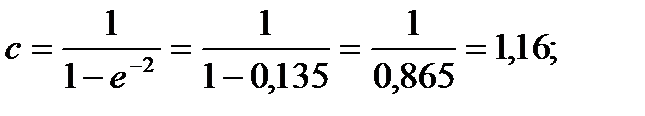
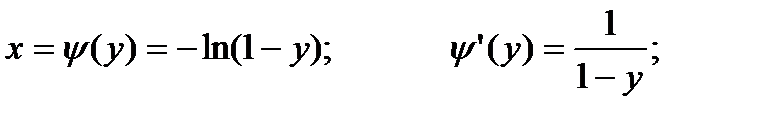
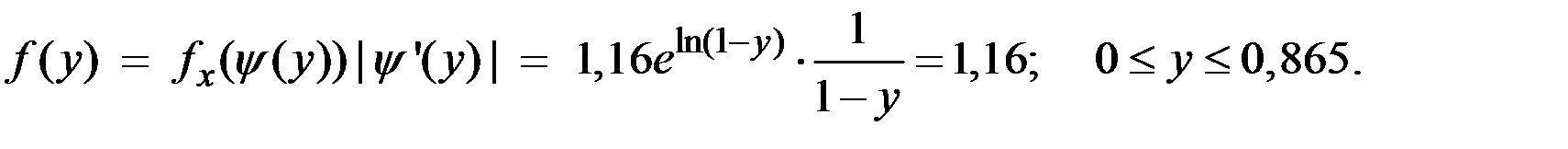
4.2. Числовые характеристики функций случайных величин
Часто на практике возникает задача определения числовых характеристик функций случайных величин помимо законов распределения этих функций.
Если X – дискретная случайная величина с рядом распределения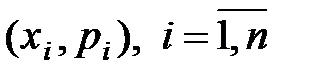 
, или X – непрерывная случайная величина с плотностью распределения 
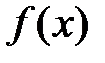, а величина 
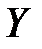связана с X функциональной зависимостью 
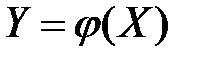, то математическое ожидание величины 
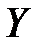равно
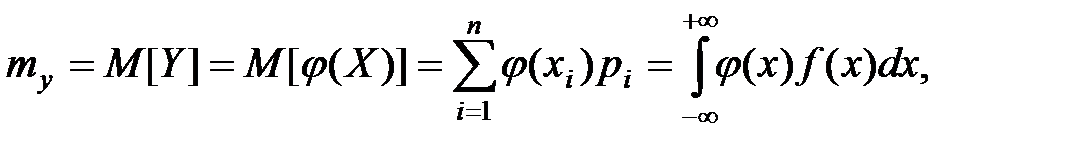
а дисперсия Y выражается для дискретной и непрерывной СВ формулами:
.
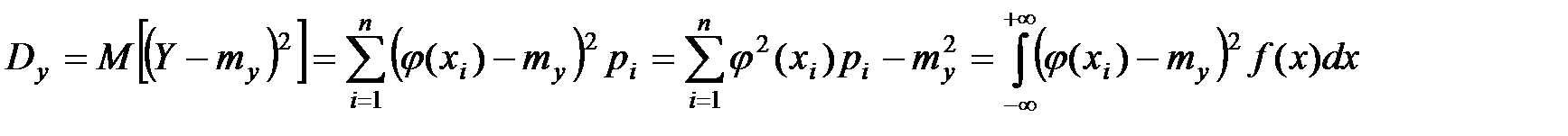Если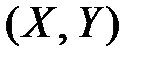 
– система двух дискретных случайных величин, распределение которой характеризуется вероятностями 
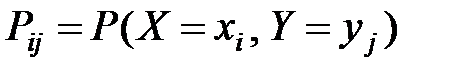, или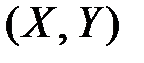 
– система двух непрерывных случайных величин с плотностью распределения 
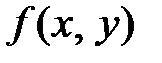, а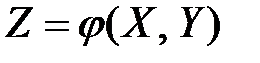 
, то математическое ожидание и дисперсия величины 
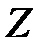вычисляются по соотношениям:
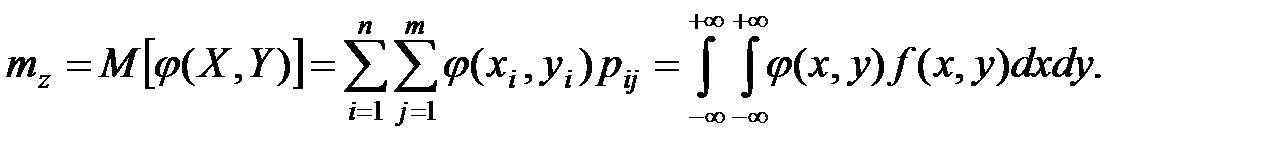
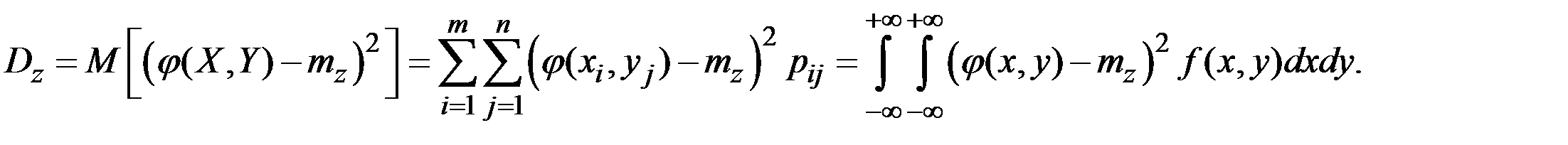
Частные случаи.
Если X – случайная величина, а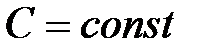 
, то справедливы соотношения:
, 
, 
.
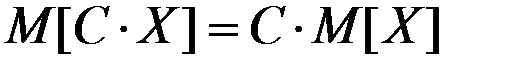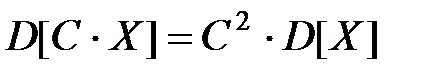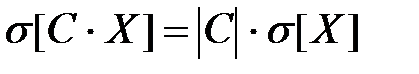Математическое ожидание линейной функции нескольких случайных величин
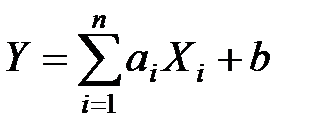
равно той же линейной функции от их математических ожиданий
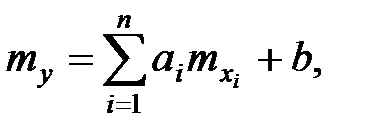
а дисперсия в этом случае равна
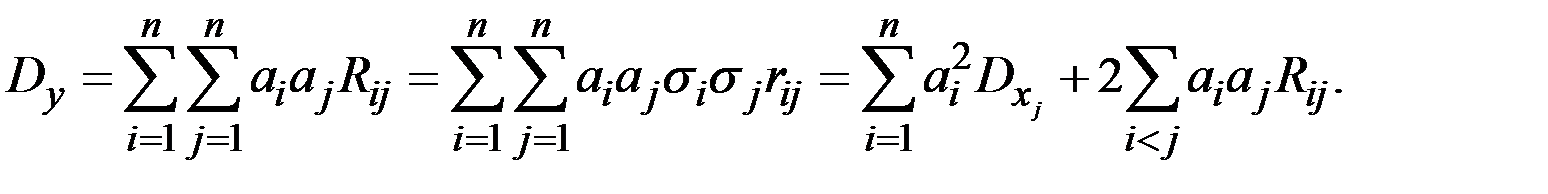
Математическое ожидание произведения двух величин определяется соотношением
.
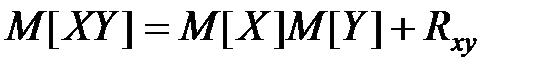В частности:
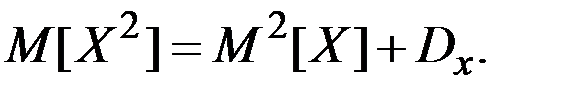
Дисперсия произведения двух независимых случайных величин X и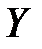 
выражается формулой
.
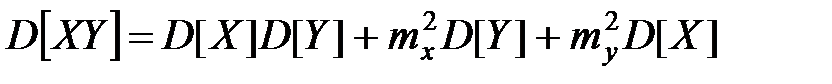На практике часто встречаются случаи, когда исследуемая функция случайных величин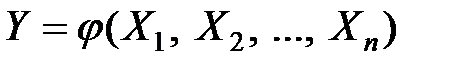 
не является линейной.
В этом случае можно использовать линеаризацию.
Математическое ожидание и дисперсия в этом случае вычисляются по формулам:
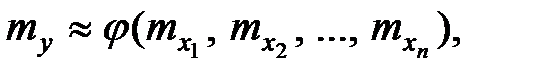
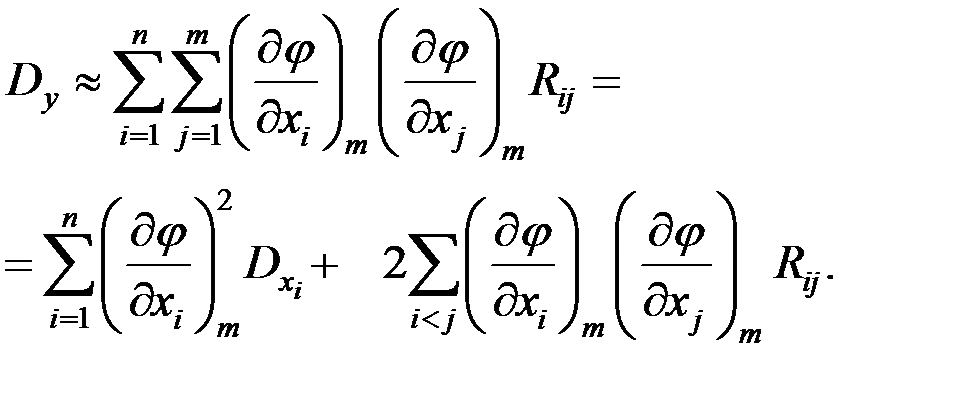
Символ m у скобок указывает, что соответствующие производные вычисляются в точках математических ожиданий.
Пример 4.4. Ошибка некоторого прибора выражается функцией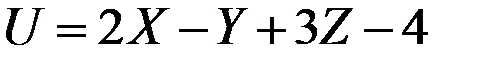 
, где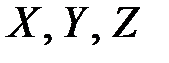 
– так называемые первичные ошибки, представляющие собой систему случайных величин, которая характеризуется математическими ожиданиями 
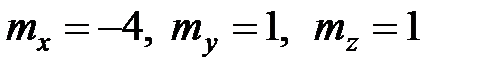и корреляционной матрицей 
.
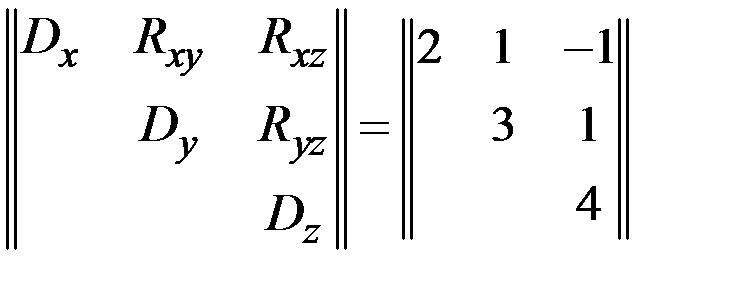Найти математическое ожидание и дисперсию ошибки прибора.
Решение. Так как функция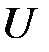 
линейна, то
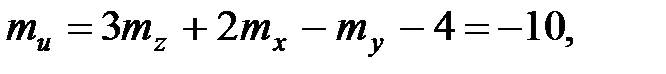
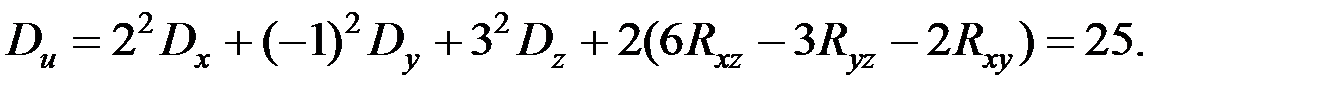
Пример 4.5. Абсцисса точки попадания снаряда выражается формулой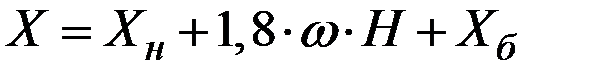 
, где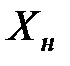 
(ошибка наводки, м), 
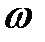(угловая скорость, рад/сек), 
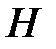(дальность стрельбы, м), 
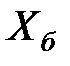(баллистическая ошибка, м) представляют собой случайные величины с математическими ожиданиями 
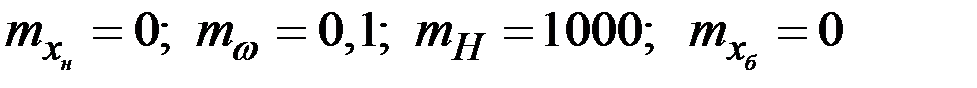и средними квадратическими отклонениями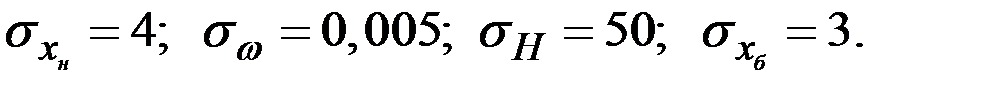 
Нормированная корреляционная матрица системы имеет вид:
Найти мат. ожидание и среднее квадратич. отклонение величины X.
Решение. Применяем формулы для нелинейной функции.
Подставляя в исходную формулу математические ожидания аргументов, имеем математическое ожидание величины X:
.
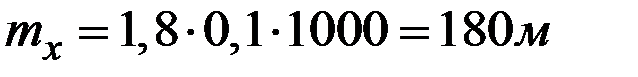Для определения среднего квадратического отклонения величины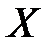 
найдём частные производные:
;
.
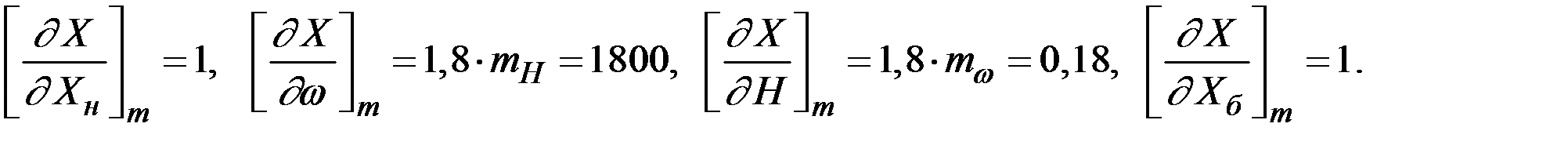
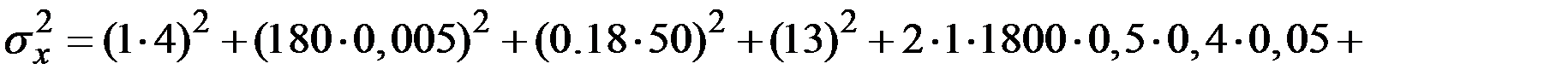
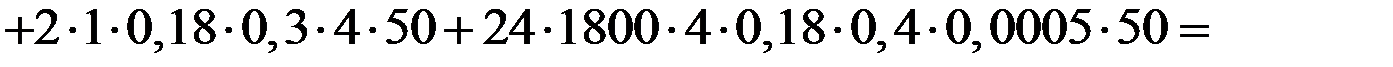
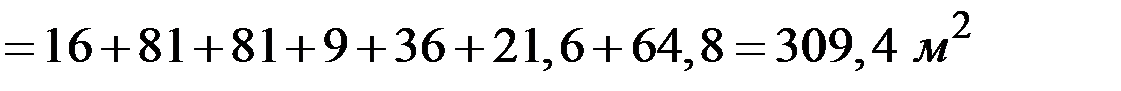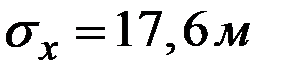Пример 4.6. На окружности радиуса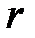 
случайным образом располагаются две точки, которые затем соединяются между собой и с центром окружности. Найти мат. ожидание площади полученного треугольника.
Решение. Если зафиксировать одну точку, то другая полностью определяется равномерно распределённым случайным углом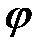 
, образованным радиусами, проведёнными к этим точкам из центра круга.
Имеем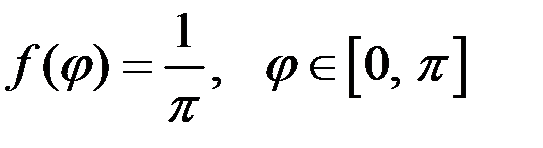 
, 
.
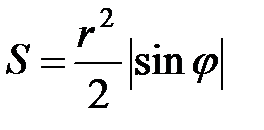Тогда математическое ожидание площади треугольника
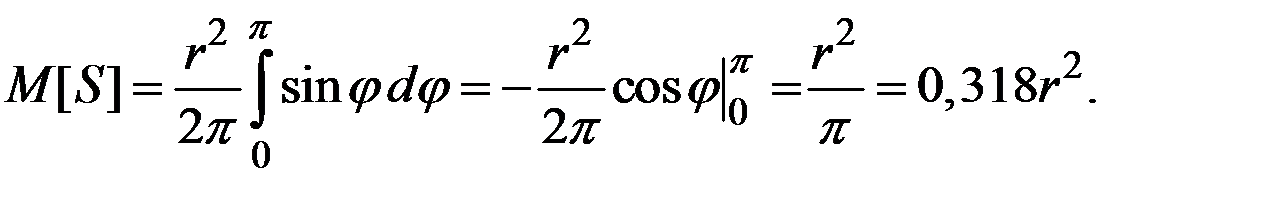
Пример 4.7. Величина Х имеет характеристики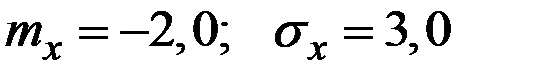 
.
Величина Y связана с Х зависимостью Y = 3 – 5 Х.
Вычислить характеристики: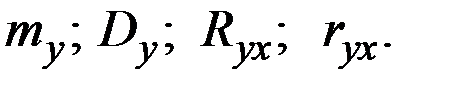 
Решение. Используем соотношения для основных числовых характеристик линейных преобразований.
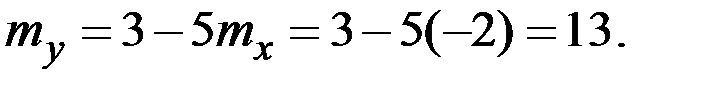
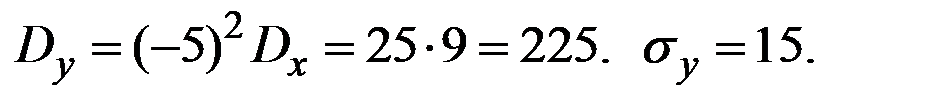
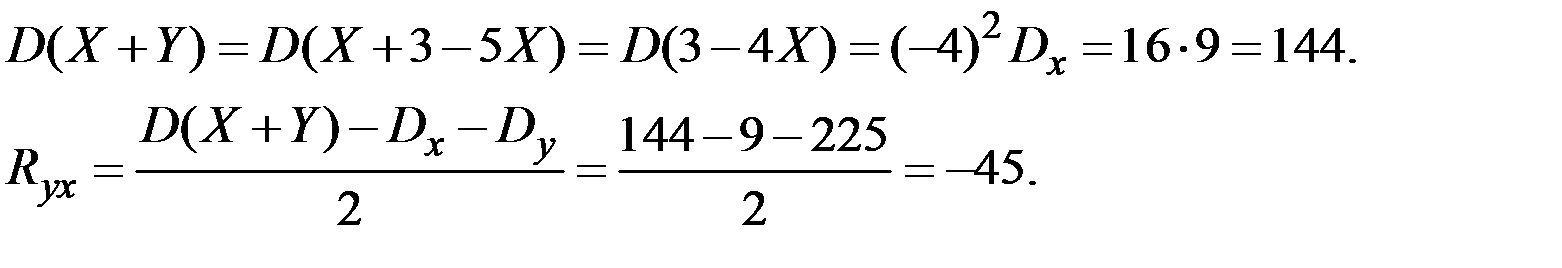
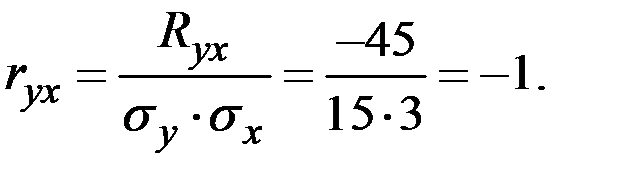
Пример 4.8. Стержень длиной 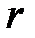закреплён в одной точке и случайно вращается так, что все его направления равновероятны. Найти математическое ожидание проекции этого стержня на неподвижную ось.
Решение. Если зафиксировать одну точку, то другая полностью определяется равномерно распределённым случайным углом 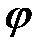, образованным радиусами, проведёнными к этим точкам из центра круга.
Имеем .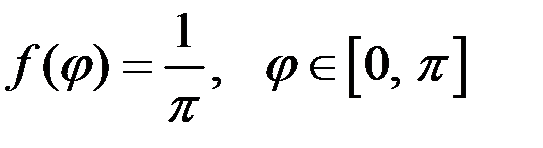
Проекция стержня определяется выражением: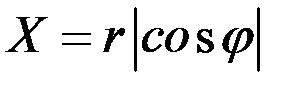 
.
Тогда математическое ожидание проекции
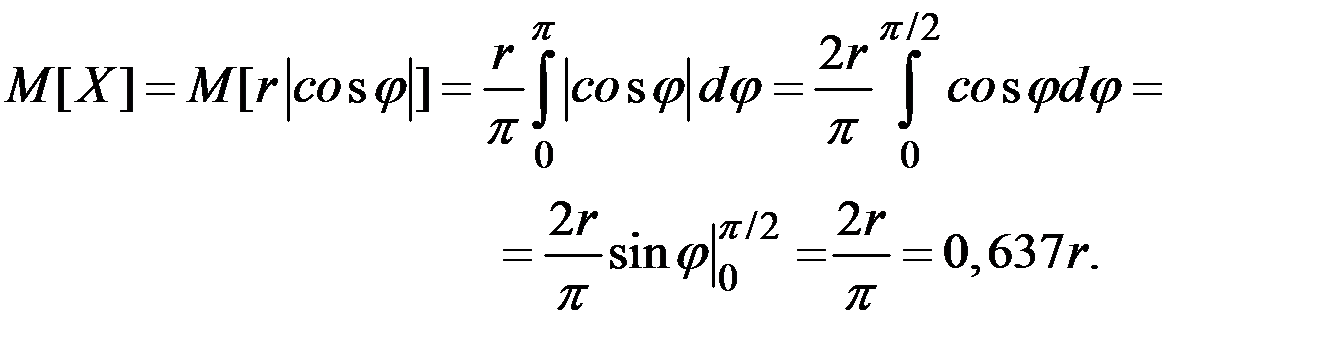
Пример 4.9. Размеры квадратного листа фанеры равномерно распределены в интервале от 10 до 12 сантиметров. Найти среднюю площадь листа.
Решение. У равномерного распределения имеем параметры
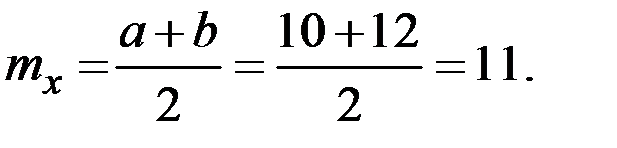
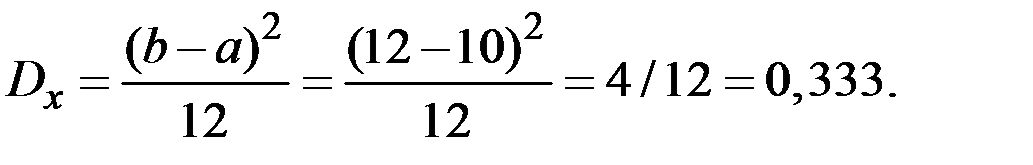
Тогда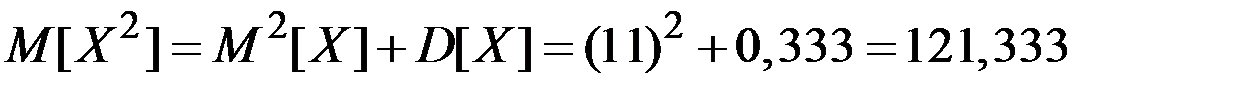 
(см.)2.
4.3. Композиция законов распределения
На практике иногда требуется найти закон распределения суммы двух случайных величин.
Если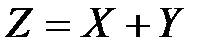 
, то плотность распределения величины 
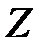определяется из двумерного закона 
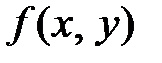по соотношению
.
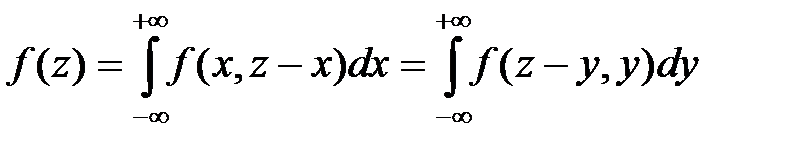Есл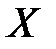и 
и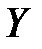 
независимые величины, то говорят о композиции законов распределения.
Тогда
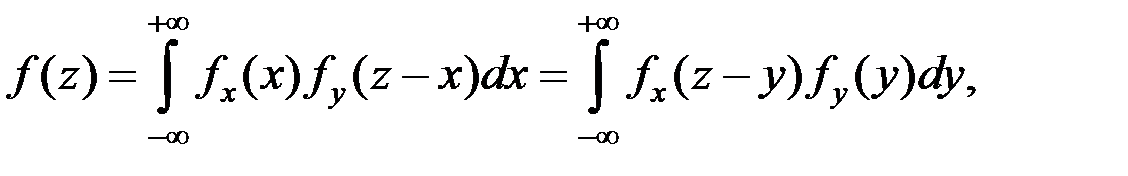
где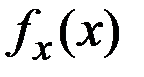 
и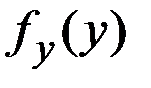 
– законы распределения X и 
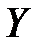соответственно.
При вычислении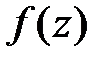 
по приведённым формулам важно правильно определить область существования соответствующего интеграла при известных ограничениях на величины X и 
.
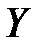Пример 4.10. Технологический процесс обработки деталей состоит из двух этапов. На каждом этапе имеется накопительный бункер. Из первого бункера детали забираются на дальнейшую обработку регулярно через каждые 2 минуты, а из второго – регулярно через каждые 10 минут. Найти закон распределения суммарного времени нахождения детали в бункерах.
Решение. Пусть X – время нахождения детали в первом бункере, а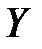 
– во втором. По известным законам распределения X и 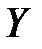найдём закон распределения их суммы 
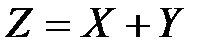. Имее6м:
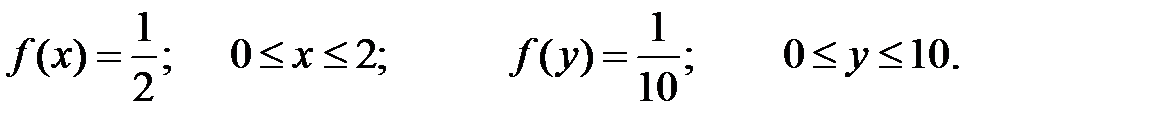
По формуле свёртки получим
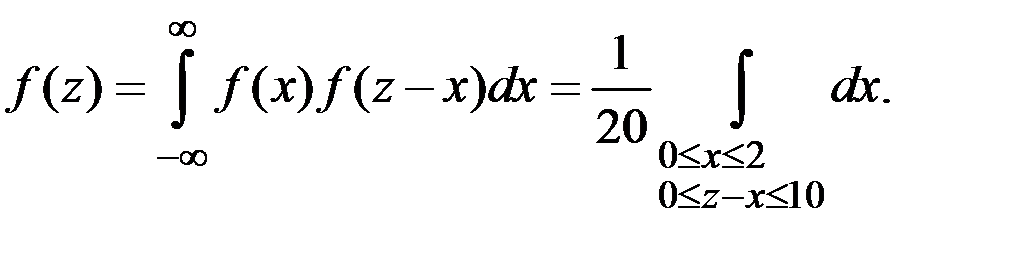
Для нахождения интеграла разобьём интервал изменения величины z на 5 частей (рис. 4.3).
1. При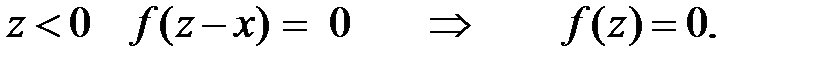 
2. При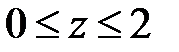 
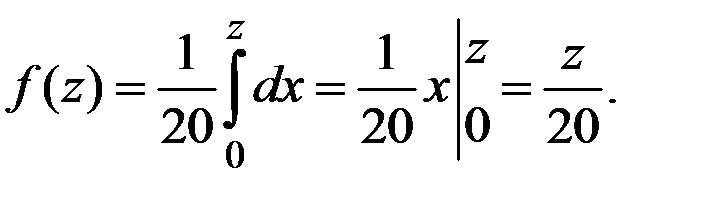
3. При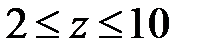 
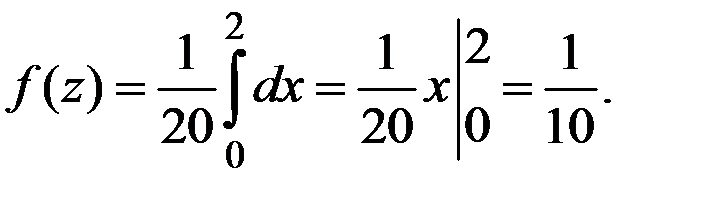
4. При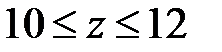 
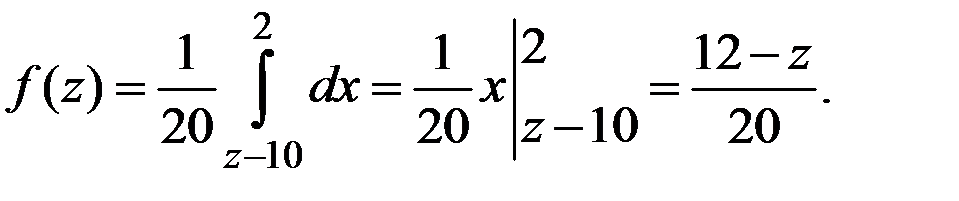
5. При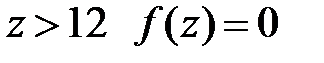 
.
Рис. 4.3. Графическое представление области интегрирования
и результата свёртки
Окончательно получаем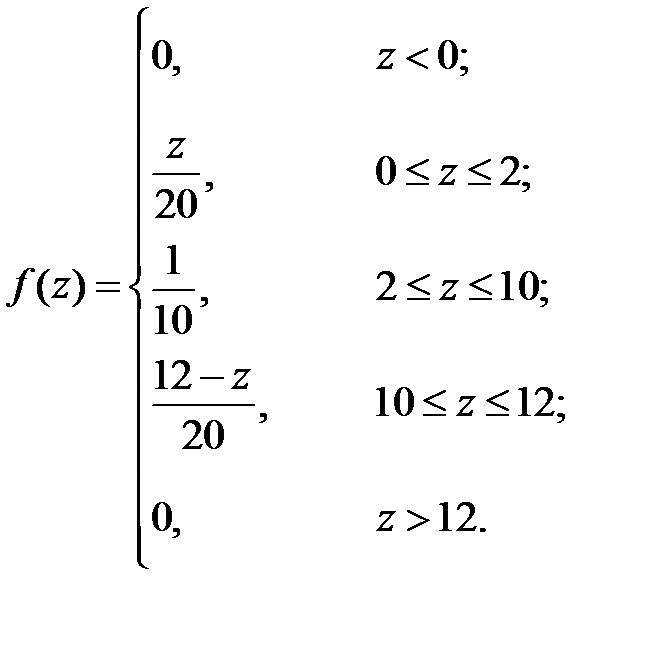 
Закон распределения называется устойчивым, если при композиции двух законов одного типа вновь получается закон этого же типа.
В частности при композиции нормальных законов получается снова нормальный закон, причём математические ожидания и дисперсии суммируются.
То есть, если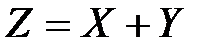 
, а
, 
,
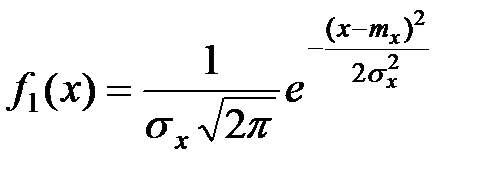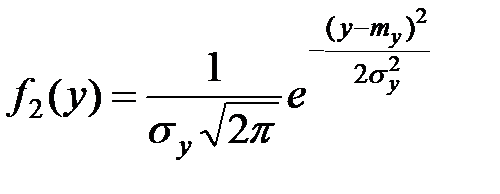то
.
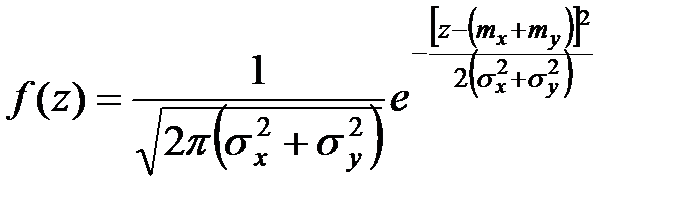Правило композиции нормальных законов может быть обобщено на случай произвольного числа независимых случайных величин.