Задания для контрольной работы № 3
Задание 3.1. Первая бригада за смену произвела А1 деталей первого сорта, В1 деталей второго сорта, С1 деталей третьего сорта (табл. 3.2). Вторая бригада соответственно: А2, В2, С2. На экспертизу случайным образом отобрали по одной детали из продукции этих бригад. Пусть X – сорт детали, взятой у первой бригады. Y – сорт детали, взятой у второй бригады. Составить закон распределения системы двух случайных величин (Х, Y) и найти их математические ожидания и средние квадратические отклонения.
Таблица 3.2
Варианты задания № 3.1
| № варианта | Значения параметров | |||||
| А1 | В1 | С1 | А2 | В2 | С2 | |
| 1 | 4 | 2 | 3 | 5 | 2 | 6 |
| 2 | 3 | 4 | 0 | 3 | 6 | 1 |
| 3 | 5 | 4 | 1 | 6 | 2 | 8 |
| 4 | 2 | 4 | 6 | 1 | 3 | 5 |
| 5 | 3 | 7 | 2 | 10 | 2 | 8 |
| 6 | 2 | 7 | 11 | 3 | 5 | 2 |
| 7 | 10 | 8 | 2 | 1 | 8 | 11 |
| 8 | 3 | 4 | 13 | 10 | 9 | 1 |
| 9 | 8 | 2 | 0 | 13 | 8 | 2 |
| 10 | 7 | 0 | 3 | 7 | 4 | 3 |
| 11 | 8 | 4 | 2 | 7 | 3 | 5 |
| 12 | 4 | 5 | 1 | 1 | 3 | 6 |
| 13 | 2 | 7 | 1 | 2 | 1 | 5 |
| 14 | 3 | 14 | 13 | 3 | 2 | 1 |
| 15 | 2 | 3 | 4 | 7 | 8 | 5 |
| 16 | 1 | 2 | 3 | 3 | 4 | 0 |
| 17 | 3 | 1 | 4 | 4 | 0 | 6 |
| 18 | 4 | 2 | 7 | 5 | 9 | 6 |
| 19 | 1 | 4 | 8 | 2 | 8 | 0 |
| 20 | 0 | 7 | 12 | 4 | 5 | 1 |
| 21 | 1 | 2 | 3 | 0 | 5 | 15 |
| 22 | 4 | 7 | 2 | 5 | 25 | 0 |
| 23 | 1 | 0 | 8 | 6 | 3 | 1 |
| 24 | 9 | 11 | 3 | 7 | 2 | 1 |
| 25 | 2 | 7 | 1 | 4 | 6 | 10 |
| 26 | 7 | 14 | 6 | 2 | 3 | 3 |
| 27 | 8 | 1 | 8 | 9 | 5 | 4 |
| 28 | 4 | 2 | 4 | 8 | 4 | 8 |
| 29 | 2 | 5 | 3 | 3 | 6 | 7 |
| 30 | 3 | 7 | 1 | 4 | 2 | 6 |
Задание № 3.2. Получить и построить графики уравнений регрессии для случайных величин (Х, Y), распределённых по нормальному закону и составляющих систему с параметрами: m x, m y, D x, D y, R xy (табл. 3.3).
Таблица 3.3
Варианты задания № 3.2
| № варианта | Значения параметров | ||||
| m x | m y | D x | D y | R xy | |
| 1 | 3 | 4 | 0,5 | 1,3 | 0,7 |
| 2 | 10 | 2 | 4 | 1 | 1,5 |
| 3 | –4 | 25 | 2,5 | 9 | 3 |
| 4 | 15 | 10 | 4 | 16 | 6 |
| 5 | 26 | 115 | 1 | 4 | 1,4 |
| 6 | –20 | –30 | 3 | 10 | 2,4 |
| 7 | 18 | 115 | 4 | 16 | 6,4 |
| 8 | 30 | 85 | 1 | 25 | 4,5 |
| 9 | 40 | 4,3 | 4 | 0,25 | 0,9 |
| 10 | 8 | 20 | 0,16 | 4 | 0,56 |
| 11 | –12 | 7 | 4 | 2 | 2,2 |
| 12 | –33 | 90 | 10 | 15 | 10 |
| 13 | 40 | 40 | 2 | 5 | 2,5 |
| 14 | –50 | 170 | 3 | 10 | 5 |
| 15 | –120 | 80 | 36 | 4 | 8,4 |
| 16 | 250 | 45 | 21 | 7 | 9 |
| 17 | 74 | 30 | 8 | 2 | 3,6 |
| 18 | 80 | 1,8 | 6 | 0,4 | 1,1 |
| 19 | 90 | 2,5 | 5 | 0,8 | 1,8 |
| 20 | 100 | 2,6 | 8 | 0,4 | 1,5 |
| 21 | –70 | 15 | 5 | 1,3 | 2,0 |
| 22 | –66 | 22 | 13 | 0,6 | 2,1 |
| 23 | –34 | 42 | 0,5 | 2,5 | 1,0 |
| 24 | 85 | 70 | 0,6 | 4,5 | 1,2 |
| 25 | 60 | 30 | 0,7 | 1,3 | 0,8 |
| 26 | 8 | 11 | 10 | 15 | 3 |
| 27 | 30 | 5 | 2 | 5 | 6 |
| 28 | 40 | 85 | 3 | 10 | 1,4 |
| 29 | 8 | 43 | 36 | 4 | 5 |
| 30 | –12 | 20 | 15 | 7 | 4 |
Задание № 3.3. В продукции завода брак вследствие дефекта инструментов (оборудования) составляет a %, а вследствие некачественного сырья (материалов) – b%. Годная продукция составляет g % (табл. 3.4).
Найти коэффициент корреляции дефектов инструмента и сырья.
Таблица 3.4
Варианты задания № 3.3
| № варианта | Значения параметров | ||
| a, % | b, % | g, % | |
| 1 | 3,5 | 4,7 | 92,5 |
| 2 | 5,1 | 3,2 | 93,5 |
| 3 | 6,5 | 6,5 | 90,1 |
| 4 | 5,8 | 3,2 | 93,3 |
| 5 | 4,2 | 2,4 | 95,5 |
| 6 | 5,1 | 2,8 | 94,7 |
| 7 | 3,4 | 2,7 | 95,8 |
| 8 | 6,9 | 6,5 | 89,9 |
| 9 | 7,0 | 5,9 | 91,2 |
| 10 | 2,5 | 3,4 | 96,8 |
| 11 | 2,8 | 5,2 | 93,9 |
| 12 | 2,9 | 3,8 | 95,0 |
| 13 | 3,0 | 2,4 | 96,3 |
| 14 | 2,4 | 2,5 | 96,1 |
| 15 | 4,6 | 6,4 | 90,9 |
| 16 | 4,8 | 3,4 | 93,0 |
| 17 | 4,9 | 4,3 | 92,5 |
| 18 | 6,2 | 5,4 | 90,6 |
| 19 | 3,5 | 6,5 | 91,7 |
| 20 | 6,8 | 3,5 | 91,0 |
| 21 | 3,3 | 4,2 | 95,8 |
| 22 | 2,1 | 3,2 | 97,3 |
| 23 | 2,5 | 2,3 | 98,7 |
| 24 | 5,9 | 4,8 | 92,5 |
| 25 | 6,0 | 5,1 | 89,8 |
| 26 | 6,1 | 6,4 | 88,7 |
| 27 | 7,1 | 2,4 | 92,8 |
| 28 | 5,9 | 5,6 | 90,3 |
| 29 | 4,9 | 4,7 | 93,4 |
| 30 | 2,3 | 4,8 | 98,7 |
4. ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН
4.1. Законы распределения функций случайных величин
Пусть имеется непрерывная СВ X с плотностью распределения 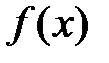 .
.
Другая СВ Y связана с ней функциональной зависимостью 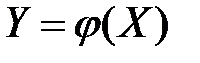 .
.
Пусть функция 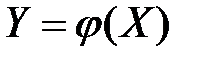 монотонная, для которой обратная функция
монотонная, для которой обратная функция 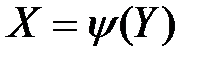 однозначная.
однозначная.
Очевидно, что вероятность 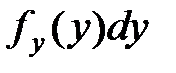 для Y из малого интервала
для Y из малого интервала 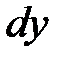 равна
равна 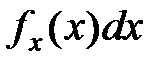 (рис. 4.1).
(рис. 4.1).

Рис. 4.1. Преобразование случайных величин
Имеем 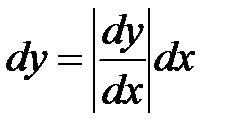 или
или 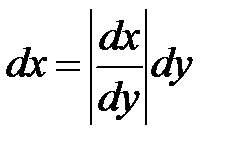 .
.
Справедливо соотношение