3.4. Совместная плотность распределения непрерывной двумерной случайной величины имеет вид

Дата: 2025-06-02; Просмотры: 20
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

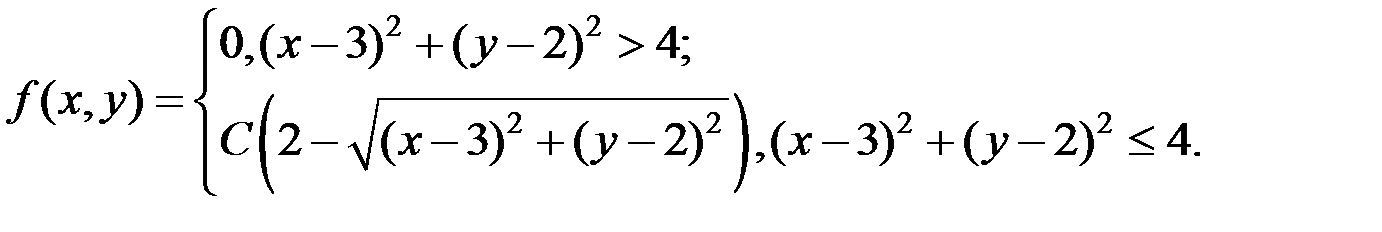
Найдите постоянную .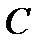

3.5. Двумерный случайный вектор 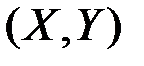распределён равномерно в треугольнике с вершинами в точках 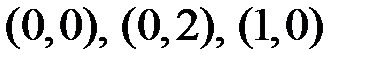. Найти условную плотность распределения случайной величины X при условии, что случайная величина Y приняла значение y.

3.6. Задана функция распределения двумерной СВ (X,Y):

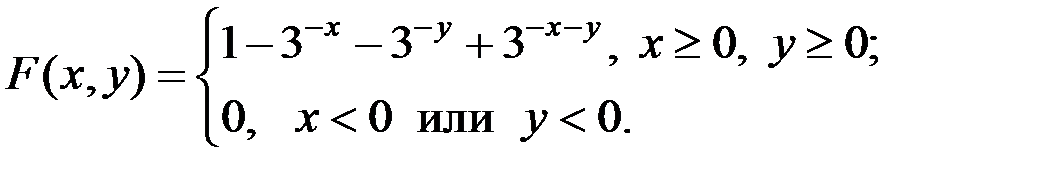
Найти вероятность попадания случайной точки в прямоугольник, ограниченный прямыми x = 0, x = p /4, y = p /6, y = p /3.

3.7. Совместная плотность распределения непрерывной двумерной случайной величины имеет вид:

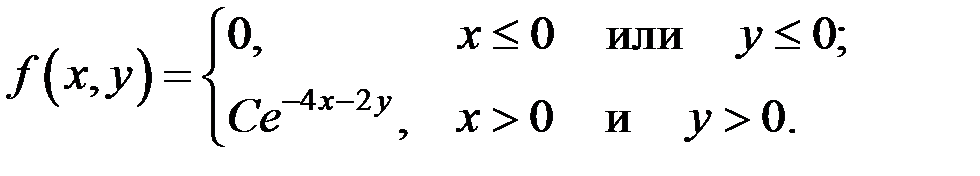
Найти постоянную C.

3.8. Условная плотность распределения случайной величины X при условии, что случайная величина Y приняла значение y, равна

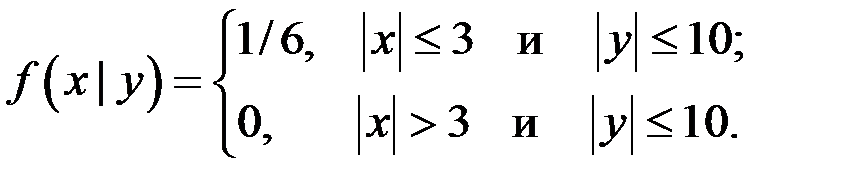
Найти условное математическое ожидание .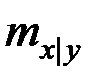

3.9. Двумерная случайная величина имеет совместную функцию распределения

.

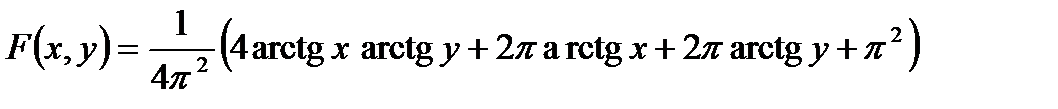Найти вероятность события .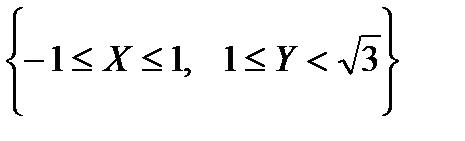

3.10. Непрерывный двумерный случайный вектор 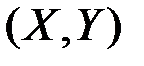имеет плотность распределения

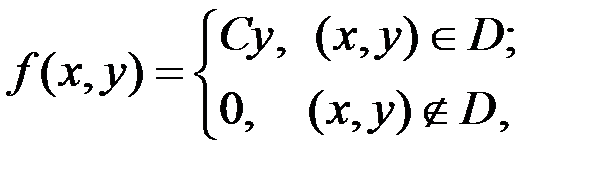
где 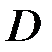– область, определения, ограниченная линиям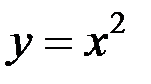и и 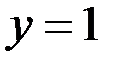. Найдите условную плотность распределения случайной величины 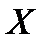, при условии, что случайная величина 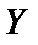приняла значение .

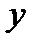3.11. Двумерная СВ 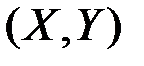имеет совместную функцию распределения

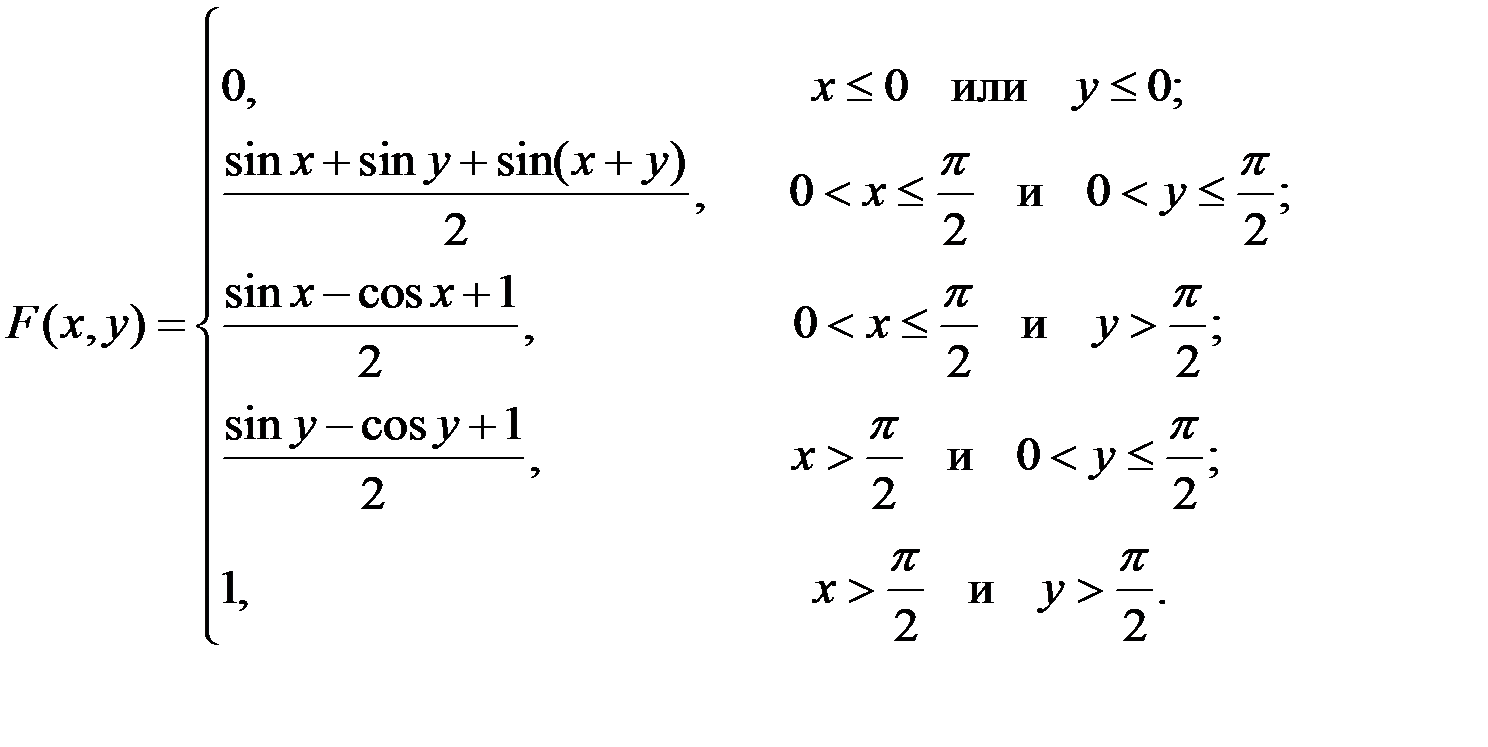
Проверьте, являются ли случайные величины 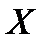и 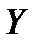независимыми.

3.12. Задана дискретная двумерная СВ :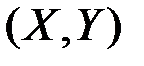

Y

X
x1 = 2 x2 = 5 x3 = 8
y1 = 0,4 0,15 0,30 0,35
y2 = 0,8 0,05 0,12 0,03

Найти условное значение математического ожидания составляющей Y при условии, что составляющая X приняла значение X = x2 = 5.

3.13. Дискретные независимые СВ заданы своими распределениями:

X 5 8 Y 1 7
P 0,2 0,8 P 0,56 0,44

Найти коэффициент вариации величины Z = X + Y.

3.14. Двумерный случайный вектор 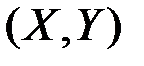имеет нормальное распределение с плотностью распределения 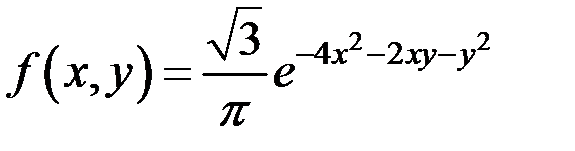. Найти условную плотность распределения случайной величины Y при условии, что случайная величина X приняла значение x.

3.15. В круге x2 + y2 £ R2 двумерная плотность вероятности имеет выражение , вне круга f(x, y) = 0. Найти постоянную С.

3.16. Задана плотность совместного распределения двумерной СВ : 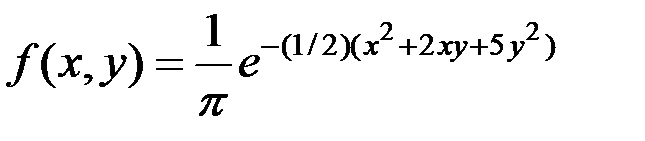. Найти плотность распределения величины Х.

3.17. Функция распределения СВ Х имеет вид F(x) = a – b arctg(x). Найти плотность распределения вероятностей, определив постоянные a и b.

3.18. В продукции завода брак вследствие дефекта А составляет 12 %, причём среди забракованной по признаку А продукции в 4 % случаев встречается дефект В, а в продукции свободной от дефекта А дефект В встречается в 2% случаев. Найти коэффициент корреляции дефектов А и В.

3.19. Система двух случайных величин подчинена закону распределения с плотностью: 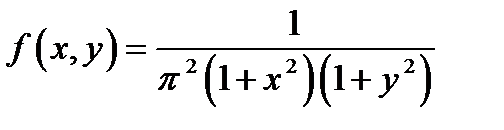. Найти функцию распределения .

3.20. Случайные величины Х, У независимы и нормально распределены с параметрами M(X) = M(У) = 0, D(X) = D(У) = 1. Найти вероятность того, что случайная точка (Х, У) попадёт в кольцо .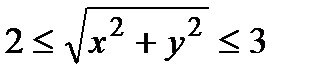

3.21. Найти плотность распределения случайной величины 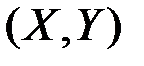если функция распределения F(x, y) = (1 - е - 2х)(1 - е - 3у) при х ³ 0, у ³ 0.

3.22. 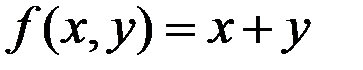при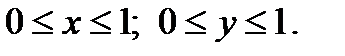

Найти значение функции регрессии 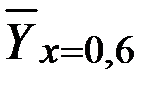(среднее значение величины Y при х = 0,6).

3.23. В одном ящике упакованы: три детали с номером 1, две детали с номером 2, четыре детали с номером 3. В другом ящике находятся: две детали с номером 1, три детали с номером 2, одна деталь с номером 3. Из каждого ящика взяли по одной детали. Пусть X – номер детали, взятой из первого ящика. Y – номер детали, взятой из второго ящика. Составить закон распределения системы двух случайных величин (Х, Y) и найти их математические ожидания, средние квадратические отклонения