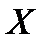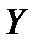3.5. Числовые характеристики системы нескольких величин
Минимальное число характеристик, с помощью которых может быть охарактеризована система n случайных величин 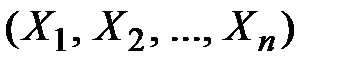 :
:
1) n математических ожиданий 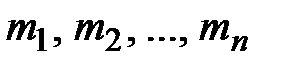 , характеризующих средние значения величин;
, характеризующих средние значения величин;
2) n дисперсий 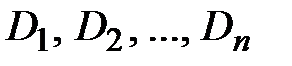 , характеризующих их рассеяние;
, характеризующих их рассеяние;
3) 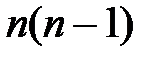 корреляционных моментов
корреляционных моментов 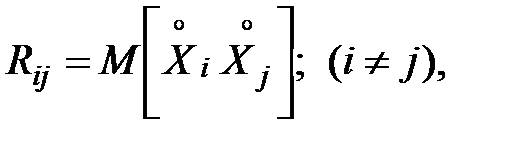
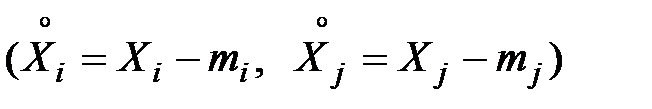 , характеризующих попарную корреляцию всех величин, входящих в систему.
, характеризующих попарную корреляцию всех величин, входящих в систему.
Дисперсия каждой из случайных величин 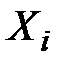 есть частный случай корреляционного момента, а именно, корреляционный момент величины
есть частный случай корреляционного момента, а именно, корреляционный момент величины 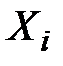 и той же величины
и той же величины 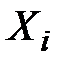 :
:
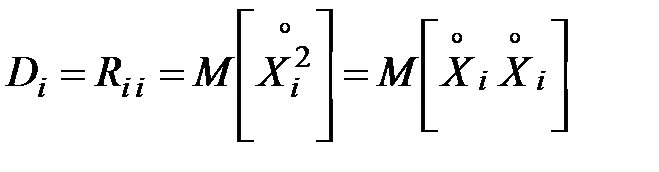 .
.
Все корреляционные моменты и дисперсии удобно располагать в виде симметричной по отношению к главной диагонали квадратной корреляционной матрицы случайных величин 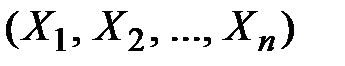 :
:
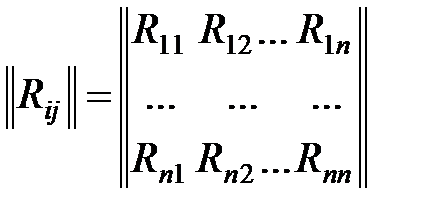 ,
,
где 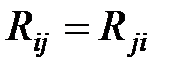 ;
; 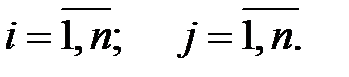
В целях наглядности суждения именно о коррелированности случайных величин безотносительно к их рассеиванию часто пользуются нормированной корреляционной матрицей 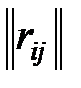 , составленной из коэффициентов корреляции
, составленной из коэффициентов корреляции
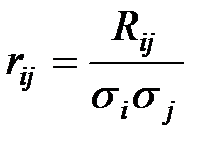 ;
; 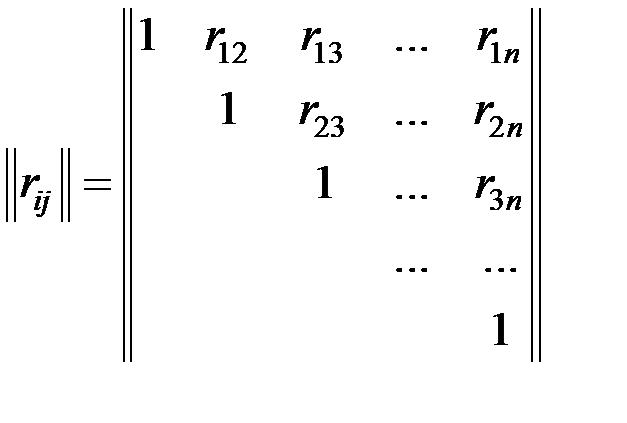 .
.
3.6. Нормальный закон распределения системы двух величин
Плотность нормального закона распределения двух случайных величин выражается формулой:
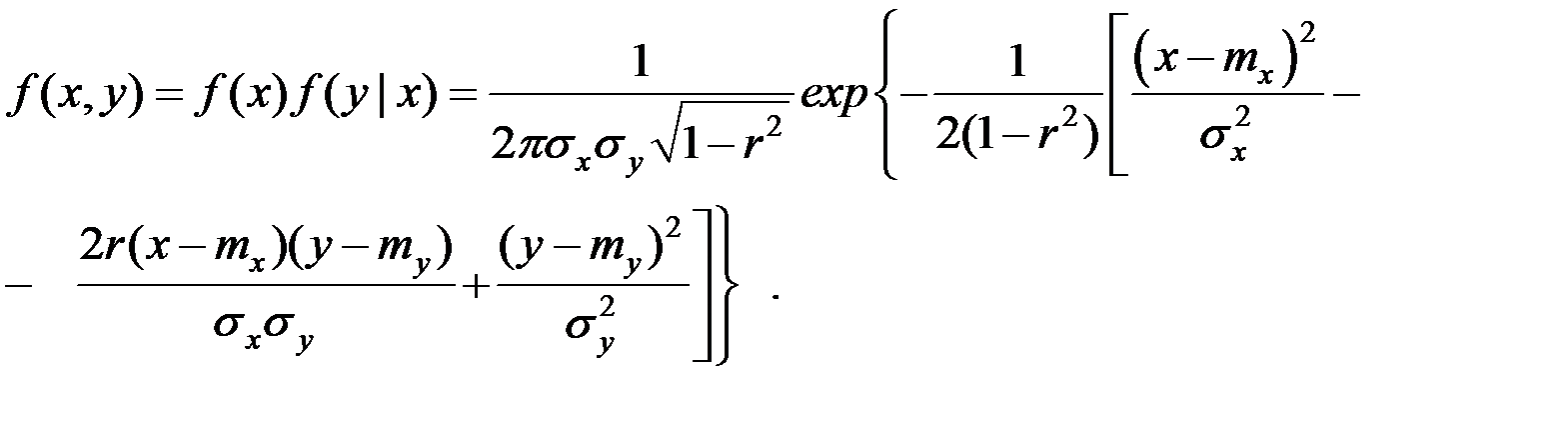
Этот закон зависит от пяти параметров: 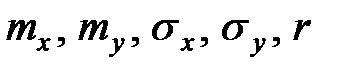 .
.
Параметры 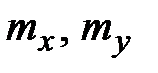 представляют собой математические ожидания (центры рассеивания) величин
представляют собой математические ожидания (центры рассеивания) величин 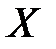 и
и 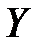 ;
; 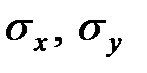 – их средние квадратические отклонения;
– их средние квадратические отклонения; 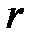 – коэффициент корреляции величин
– коэффициент корреляции величин 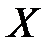 и
и 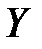 .
.
Если 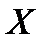 и
и 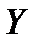 не коррелированы, то
не коррелированы, то
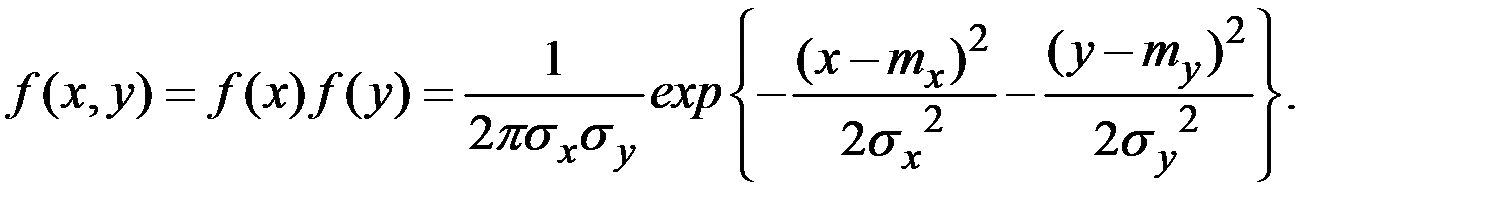
Для системы СВ, подчинённых нормальному закону, из некоррелированности величин вытекает также их независимость.
Термины "некоррелированные" и "независимые" величины для случая нормального распределения эквивалентны.
Условный закон двухмерного нормального распределения:
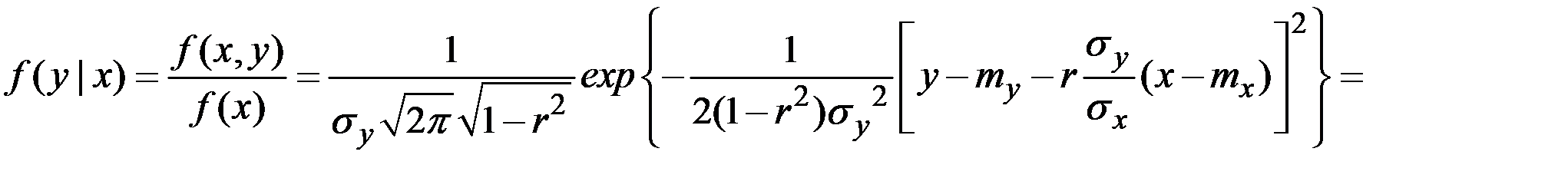
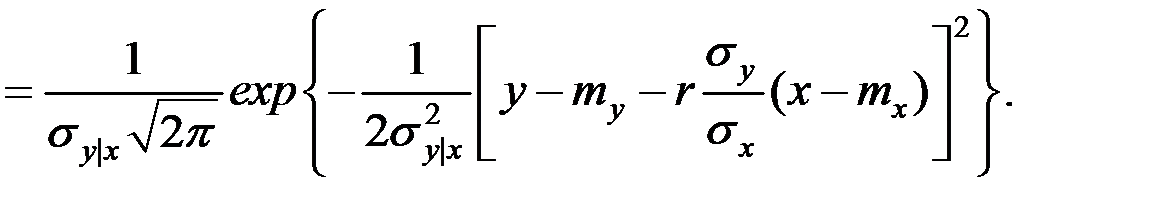
Это выражение есть плотность нормального закона с центром рассеяния
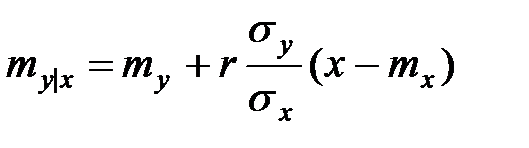
и отклонением
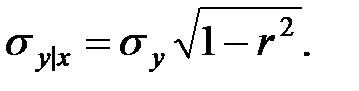
Из последних формул следует, что в условном законе распределения величины  при фиксированном
при фиксированном 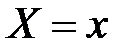 от этого значения зависит только условное математическое ожидание
от этого значения зависит только условное математическое ожидание 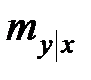 , но не дисперсия.
, но не дисперсия.
Прямая
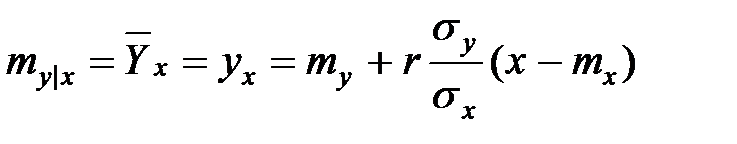
называется линией регрессии 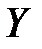 на
на 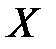 .
.
Аналогично прямая
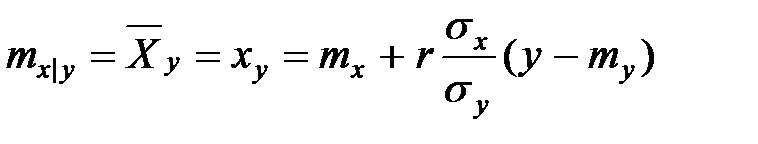
есть линия регрессии 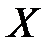 на
на 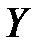 .
.
Пример 3.5. В продукции завода брак вследствие дефекта инструмента составляет 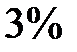 , а вследствие дефекта сырья (материала) –
, а вследствие дефекта сырья (материала) –  . Годная продукция составляет
. Годная продукция составляет 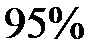 . Найти коэффициент корреляции дефектов инструмента и сырья.
. Найти коэффициент корреляции дефектов инструмента и сырья.
Решение. Пусть 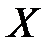 – случайная величина, принимающая значение 1, если данное изделие обладает браком вследствие дефекта инструмента, и
– случайная величина, принимающая значение 1, если данное изделие обладает браком вследствие дефекта инструмента, и 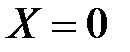 – в противном случае.
– в противном случае.
Аналогично, 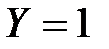 , если данное изделие обладает браком вследствие дефекта сырья, и
, если данное изделие обладает браком вследствие дефекта сырья, и 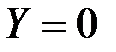 , если дефекта сырья не проявился.
, если дефекта сырья не проявился.
По условию 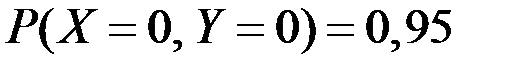 .
.
Так как
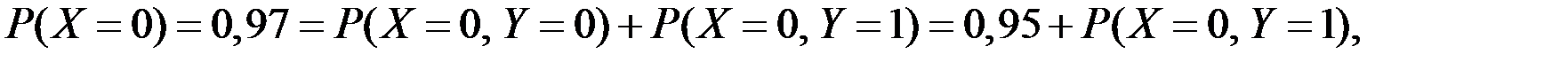 то
то 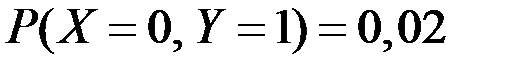 .
.
Аналогично находим
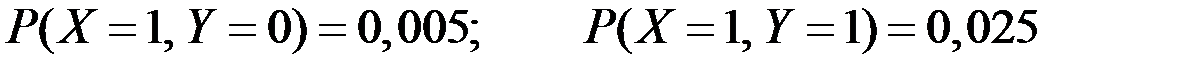 .
.
Совместное распределение величин  задаётся таблицей:
задаётся таблицей:
|
| ||
| 1 | 0 |
| 1 | 0,025 | 0,005 |
| 0 | 0,020 | 0,950 |
Тогда
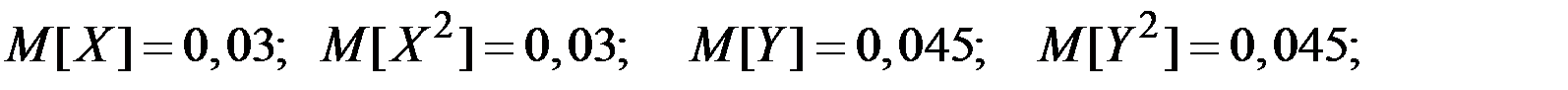
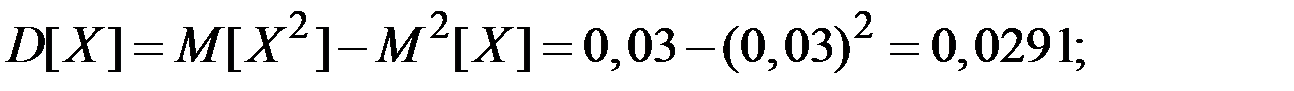
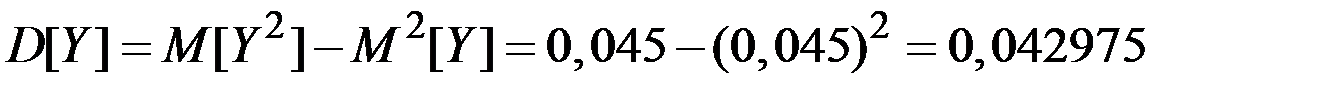 ;
;
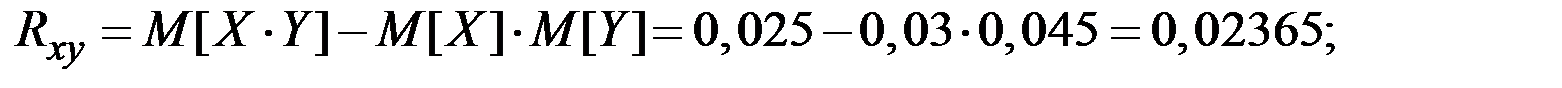
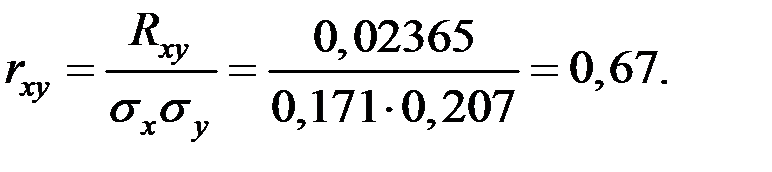
То есть, коэффициент корреляции дефектов инструмента и сырья равен 0,67.
Пример 3.6. В одном ящике упакованы: одна деталь с номером 1, две детали с номером 2, три детали с номером 3. В другом ящике находятся: две детали с номером 1, три детали с номером 2, одна деталь с номером 3. Из каждого ящика взяли по одной детали. Пусть X – номер детали, взятой из первого ящика. Y – номер детали, взятой из второго ящика. Составить закон распределения системы двух случайных величин (Х, Y) и найти их математические ожидания, средние квадратические отклонения и коэффициент корреляции.
Решение.
Вычислим вероятности событий 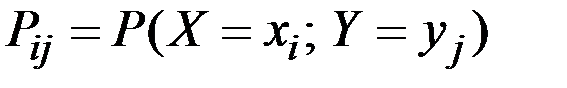 с использованием теоремы умножения вероятностей событий.
с использованием теоремы умножения вероятностей событий.
Результаты расчётов занесём в таблицу закона распределения системы двух дискретных случайных величин (Х, Y):
| 1 | 2 | 3 |
| 1 | 1/18 | 1/12 | 1/36 |
| 2 | 1/9 | 1/6 | 1/18 |
| 3 | 1/6 | 1/4 | 1/12 |
Вычислим основные числовые характеристики величин (Х, Y):
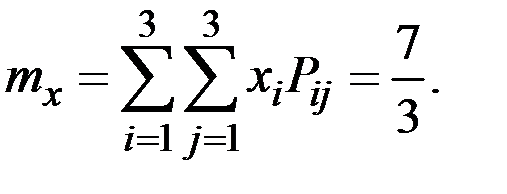
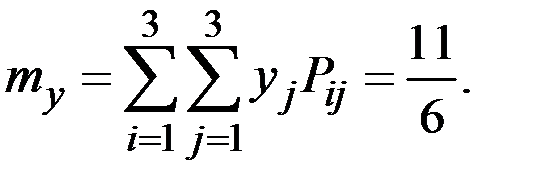
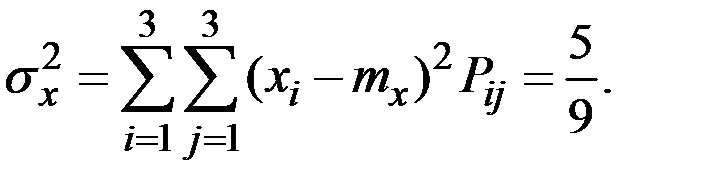
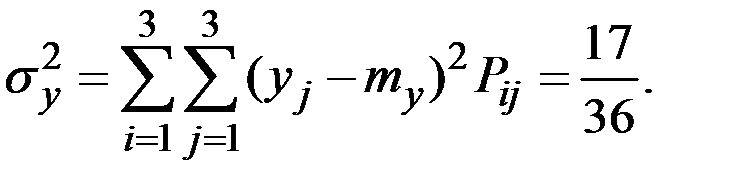
В силу независимости величин корреляция отсутствует:
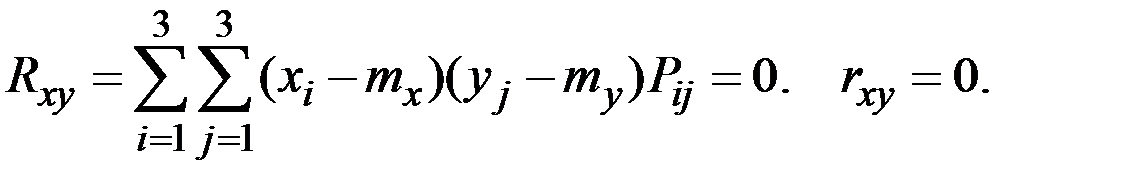
3.7. Решение типовых задач главы 3
Пример 3.7. Задана функция плотности распределения вероятностей СВ Х:
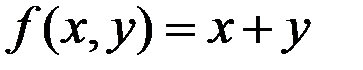 при
при 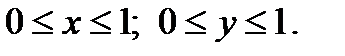
Найти значение функции регрессии 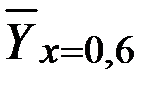 (среднее значение величины Y при х = 0,6).
(среднее значение величины Y при х = 0,6).
Решение. Найдём условный закон распределения 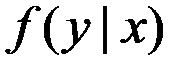 .
.
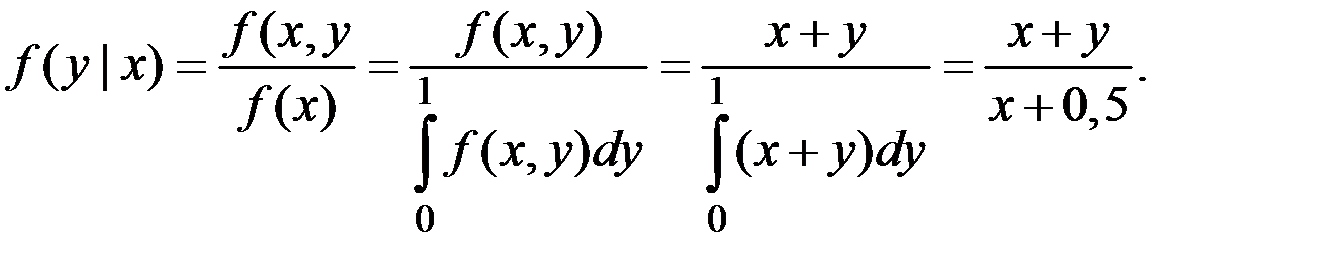
Тогда условное среднее (функции регрессии) будет иметь вид:
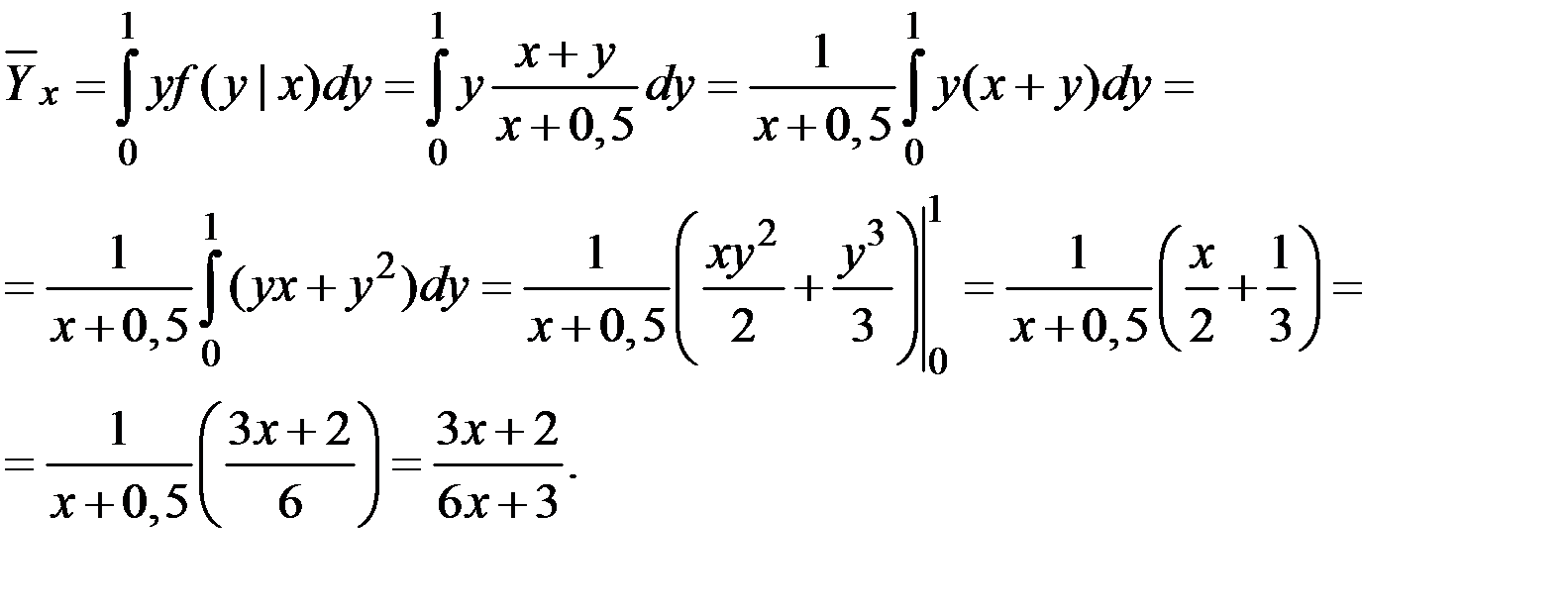
Вычислим несколько значений функции регрессии при различных аргументах.
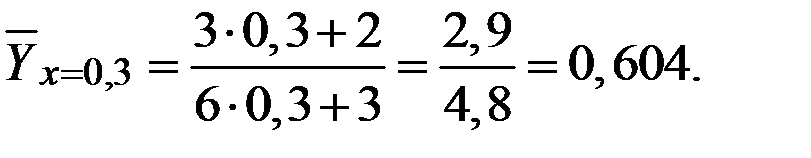
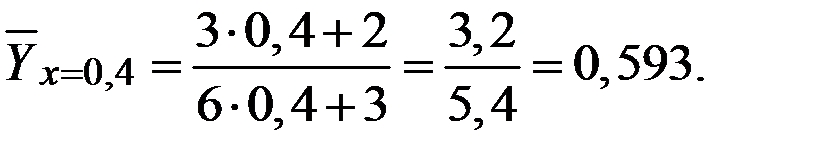
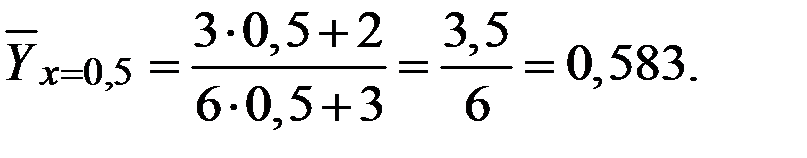
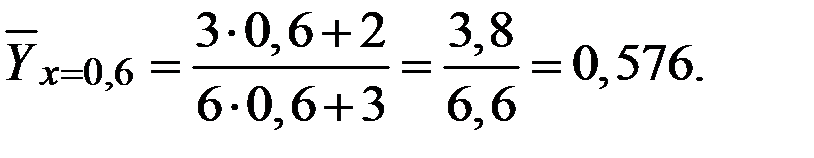
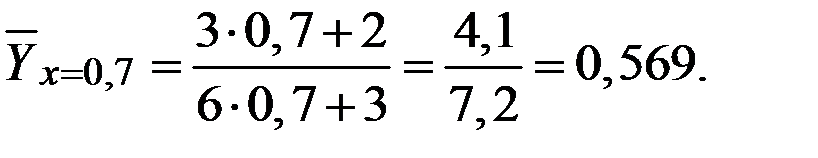
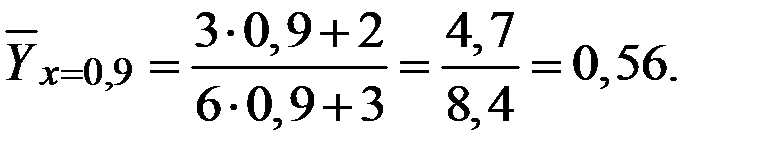
Пример 3.8. В продукции завода брак вследствие дефекта А составляет 6,1%, а вследствие дефекта В – 2,8%. Общий брак хотя бы по одному из этих дефектов составляет 7,8%. Найти коэффициент корреляции этих дефектов.
Решение. Пусть 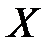 – случайная величина, принимающая значение 1, если данное изделие обладает дефектом А, и
– случайная величина, принимающая значение 1, если данное изделие обладает дефектом А, и 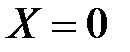 – в противном случае.
– в противном случае.
Аналогично, 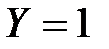 , если данное изделие обладает дефектом В, и
, если данное изделие обладает дефектом В, и 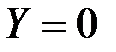 , если дефект В не проявился.
, если дефект В не проявился.
Совместное распределение величин 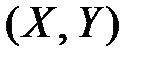 задаётся таблицей:
задаётся таблицей:
|
| ||
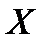
| 0 | 1 |
| 0 | 0,922 | 0,017 |
| 1 | 0,05 | 0,011 |
Тогда
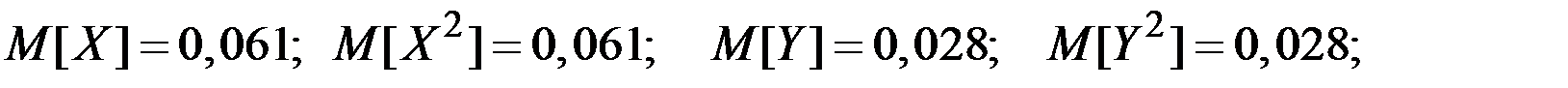
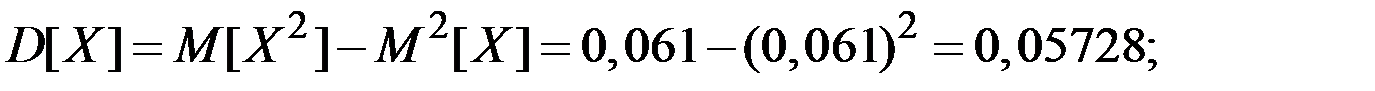
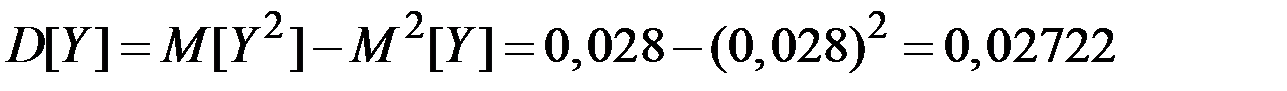 ;
;
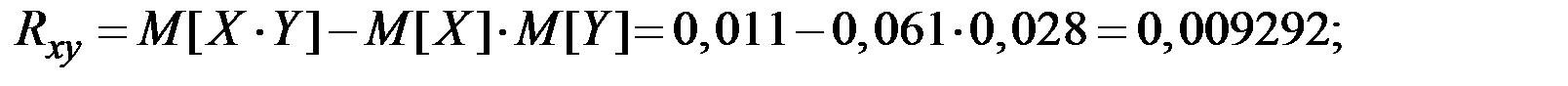
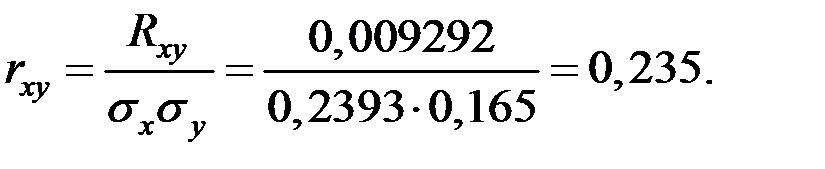
То есть, коэффициент корреляции дефектов равен 0,235.
Пример 3.9. Распределение двух СВ (X,Y) задано в таблице:
| X | Y | ||
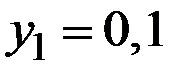
| 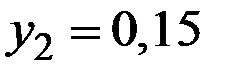
| 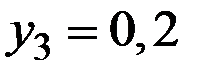
| |
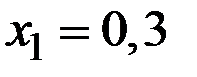
| 0,25 | 0,15 | 0,32 |
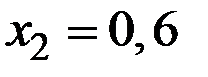
| 0,1 | 0,05 | 0,13 |
Найти условное распределение случайной величины Y при условии, что случайная величина Х приняла значения 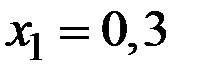 ,
, 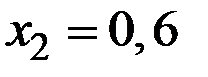 .
.
Решение. Согласно определению имеем при 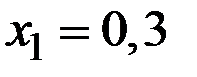 :
:
| Y | 0,10 | 0,15 | 0,20 |
| P | 0,35 | 0,21 | 0,44 |
При 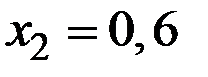 условное распределение случайной величины Y:
условное распределение случайной величины Y:
| Y | 0,10 | 0,15 | 0,20 |
| P | 0,36 | 0,18 | 0,46 |
Контрольные задачи к главе 3
3.1. Условная плотность распределения СВ X при условии, что случайная величина Y приняла значение y, равна 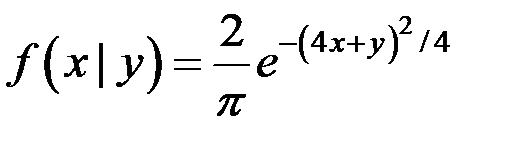 . Найти условную дисперсию
. Найти условную дисперсию 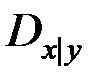 .
.
3.2. Непрерывная двумерная случайная величина 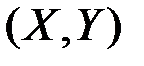 распределена равномерно в квадрате с вершина
распределена равномерно в квадрате с вершина 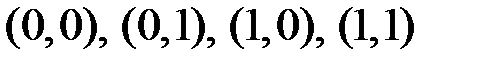 . Найдите вероятность попадания случайного вектора
. Найдите вероятность попадания случайного вектора 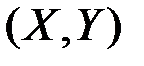 в круг
в круг 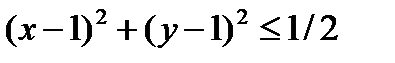 .
.
3.3. Распределение двумерного вектора 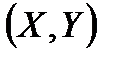 задано в таблице:
задано в таблице:
|
|
| ||
| 0,1 | 0,15 | 0,2 | |
| 0,3 | 0,25 | 0,15 | 0,32 |
| 0,6 | 0,1 | 0,05 | 0,13 |
Найти условное распределение случайной величины Y при условии, что случайная величина X приняла значение 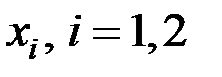 .
.