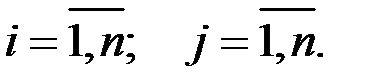3.4. Система произвольного числа случайных величин
На практике часто приходится рассматривать системы более, чем двух случайных величин.
Эти системы интерпретируются как случайные точки или случайные векторы в пространстве того или иного числа измерений.
Полной характеристикой системы произвольного числа случайных величин служит закон распределения этой системы, который может быть задан функцией распределения или плотностью распределения.
Функцией распределения системы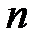 
случайных величин
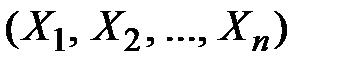называется вероятность совместного выполнения 
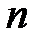неравенств вида 
:
.
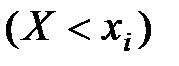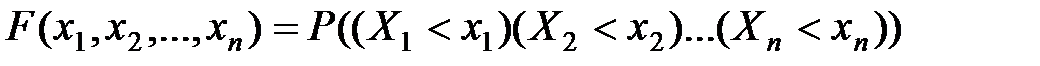Плотностью распределения системы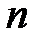 
непрерывных случайных величин называется 
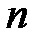–я смешанная производная функции 
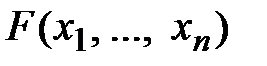, взятая один раз по каждому аргументу:
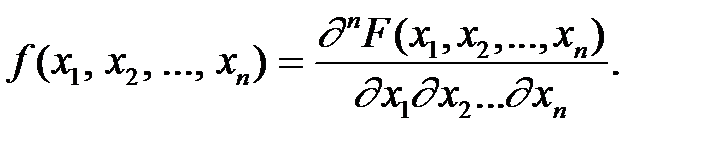
Зная закон распределения системы, можно определить законы распределения отдельных величин, входящих в систему, например:
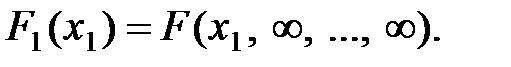
Если выделить из системы величин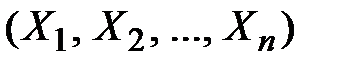 
частную систему 
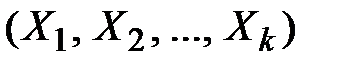, то функция распределения этой системы определяется из 
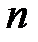–мерной функции в виде:
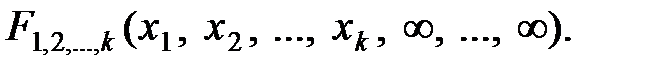
Плотность распределения каждой из величин, входящих в систему, получится, если плотность распределения системы проинтегрировать в бесконечных пределах по всем остальным аргументам:
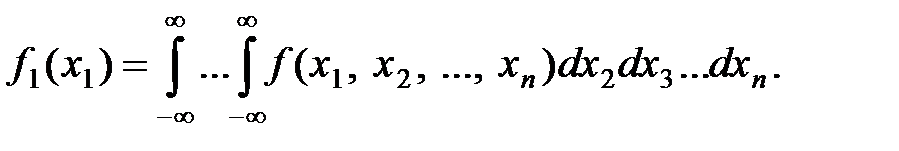
Плотность распределения частной системы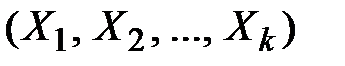 
, выделенной из системы 
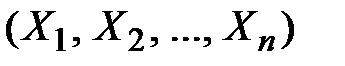определяется соотношением:
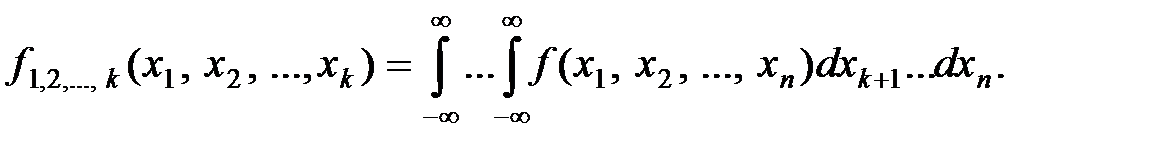
Условным законом распределения частной системы величин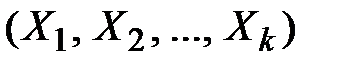 
называется её закон распределения, вычисленный при условии, что остальные величины 
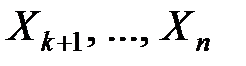приняли конкретные значения 
.
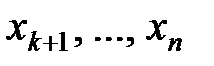Условная плотность распределения может быть вычислена по формуле:
.
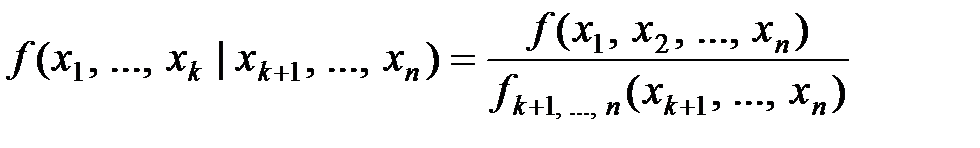Случайные величины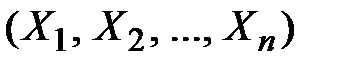 
называются независимыми, если закон распределения каждой частной системы, выделенной из системы 
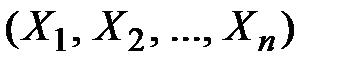, не зависит от того, какие значения приняли остальные случайные величины.
Плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в эту систему:
.
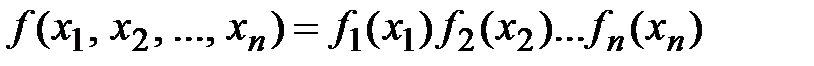В общем случае зависимых величин имеем соотношение
.
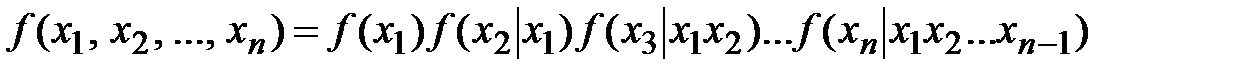Вероятность попадания случайной точки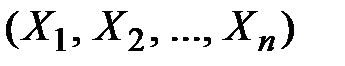 
в пределы 
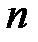–мерной области 
выражается 
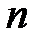–кратным интегралом:
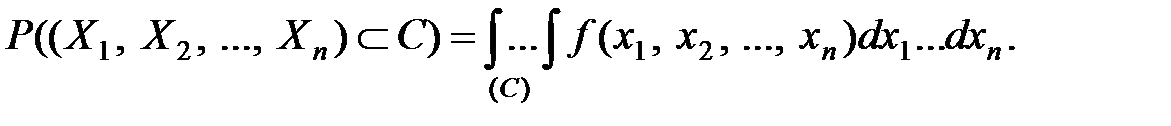
Пусть заданы две системы случайных величин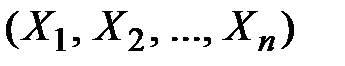 
, 
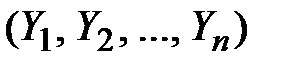или два случайных вектора в 
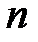–мерном пространстве: 
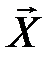с составляющим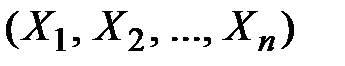и и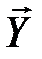 
с составляющими 
.
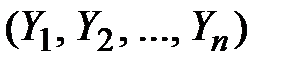Случайные векторы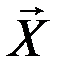 
и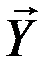 
называются некоррелированными, если каждая из составляющих вектора 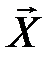не коррелирована с каждой из составляющих вектора 
:
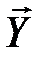