Условным законом распределения величины X, входящей в систему , называется её закон распределения, вычисленный при условии, что другая случайная величина Y приняла определённое значение y.
Зная закон распределения одной из величин и условный закон распределения другой, можно составить закон распределения системы.
Так как вероятность попадания системы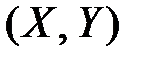 
в прямоугольник со сторонами 
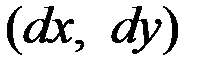, примыкающими к точке 
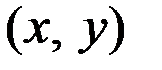есть элемент вероятности 
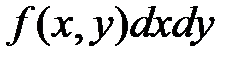, а с другой стороны это вероятность одновременного попадания случайной точки 
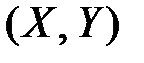в элементарную полосу, опирающуюся на отрезок 
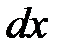, и в полосу, опирающуюся на отрезок 
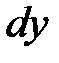, то
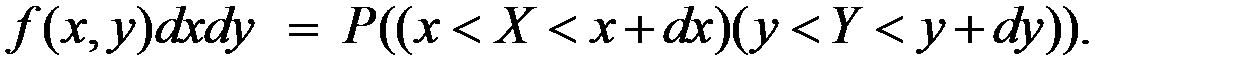
Вероятность произведения этих двух событий, по теореме умножения вероятностей, равна вероятности попадания в элементарную полосу 1, умноженную на условную вероятность попадания в элементарную полосу 2, вычисленную при условии, что первое событие имело место.
Это условие в пределе равносильно условию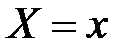 
, следовательно
.
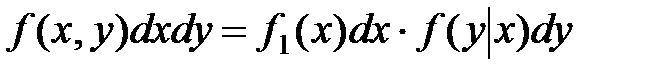Окончательно получаем:
.
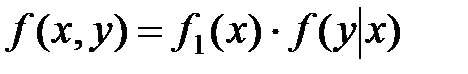Это теорема умножения законов распределения.
Аналогично
.
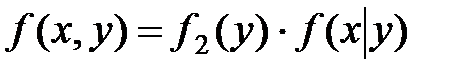Можем определить условные законы распределения через безусловные:
;
.
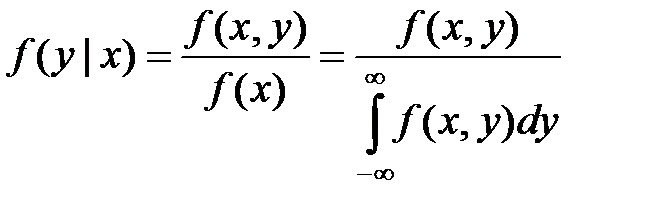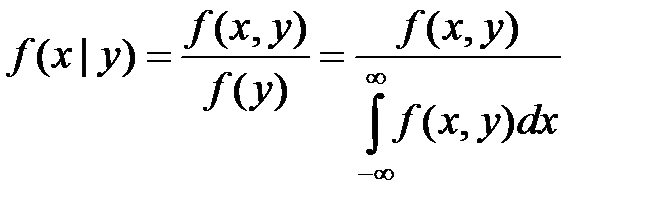Случайная величина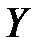 
называется независимой от случайной величины 
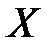, если закон распределения величины 
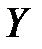не зависит от того, какое значение приняла величина 
.
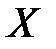Для непрерывных случайных величин условие независимости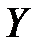 
от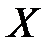 
может быть записано в виде:
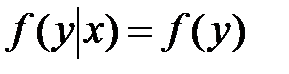при любом у.
Если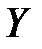 
зависит от 
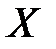, то
.
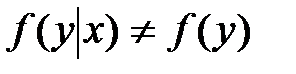Зависимость или независимость случайных величин всегда взаимны: если величина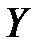 
не зависит от 
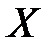, то и величина 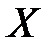не зависит от 
.
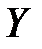Случайные величины 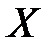и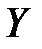 
называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины 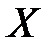и 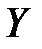называются зависимыми.
Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид:
,
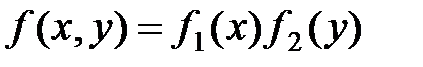т.е. плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему.
Это условие может рассматриваться как необходимое и достаточное условие независимости случайных величин.
Часто по самому виду функции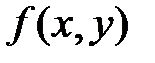 
можно заключить, что случайные величины 
, 
являются независимыми, а именно: если плотность распределения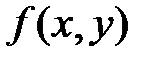 
распадается на произведение двух функций, из которых одна зависит только от x, другая – только от 
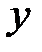, то случайные величины независимы.
Пример 3.1. Система двух случайных величин подчинена закону распределения с плотностью: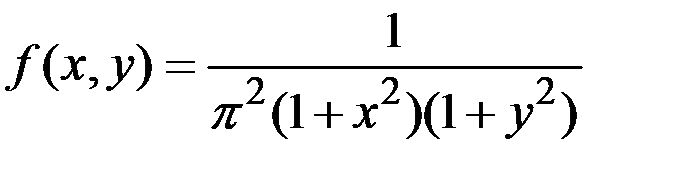 
.
Найти функцию распределения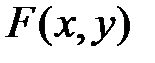 
. Определить вероятность попадания случайной точки 
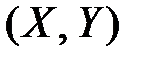в квадрат 
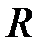с координатами: (1, 1), (0, 1), (1, 0), (0, 0).
Решение.
.
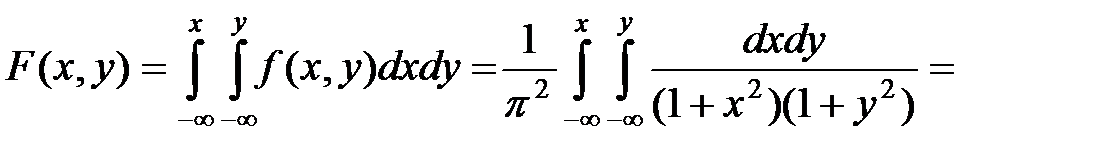
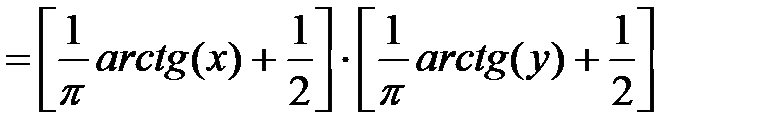Тогда вероятность попадания в квадрат (прямоугольник)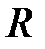 
:
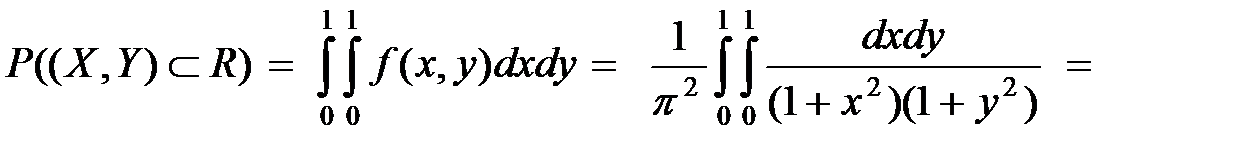
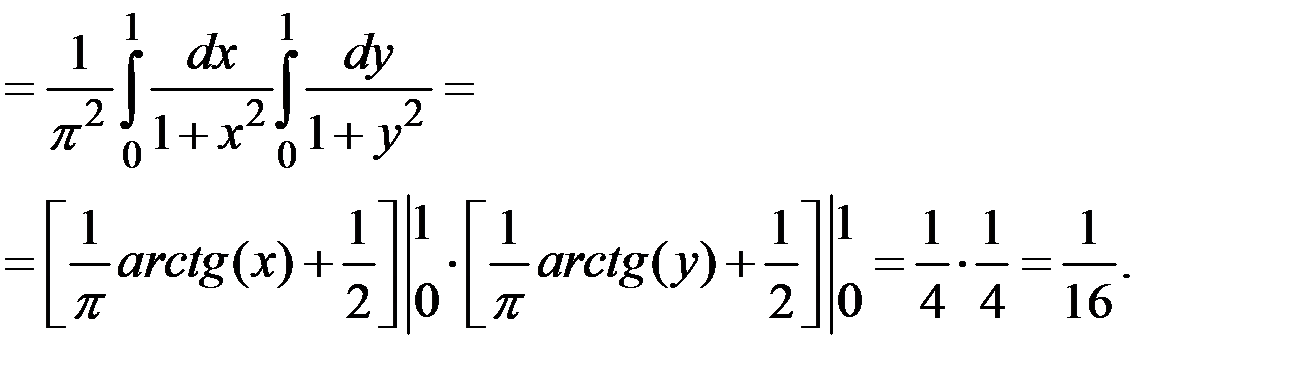
Пример 3.2. Плотность распределения системы 
имеет вид:
.
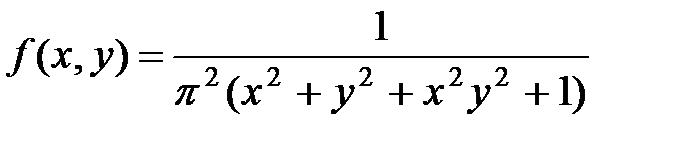Определить, зависимы или независимы величины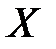 
и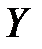 
.
Решение. Разлагая знаменатель на множители, имеем:
.
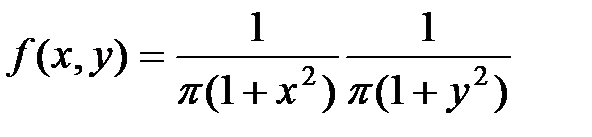Из того, что функция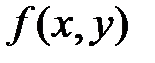 
распалась на произведение двух функций, из которых одна зависит только от 
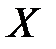, другая – только от 
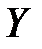, заключаем, что величины 
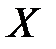и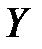 
должны быть независимы. Действительно,
.
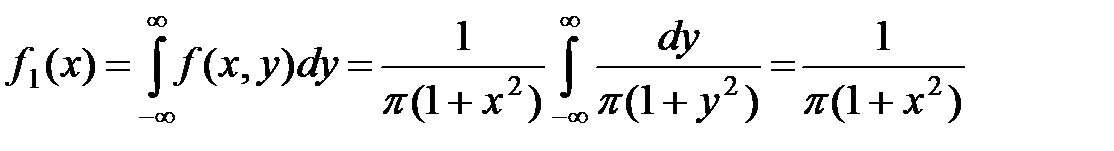Аналогично,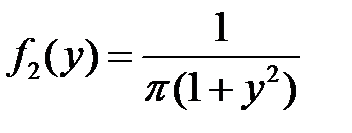 
.
Отсюда убеждаемся, что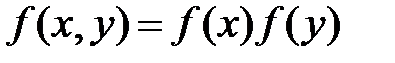 
, и, следовательно, величины 
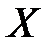и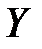 
независимы.
3.3. Числовые характеристики системы двух величин
Начальным моментом порядка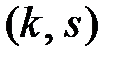 
системы 
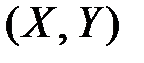называется математическое ожидание произведения 
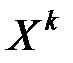на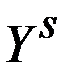 
:
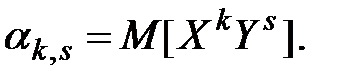
Центральным моментом порядка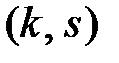 
системы 
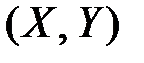называется математическое ожидание произведения 
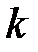–й и s–й степеней соответствующих центрированных величин:
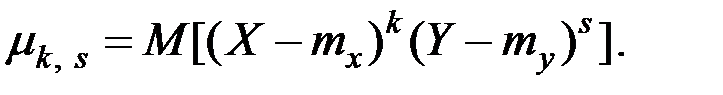
Для дискретных случайных величин начальные и центральные моменты вычисляются, соответственно, по формулам:
;
,
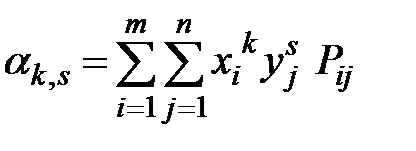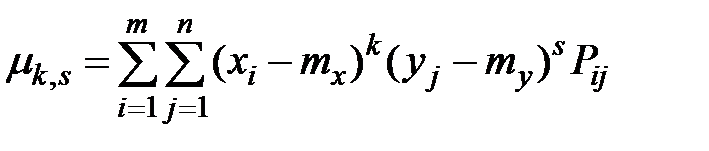где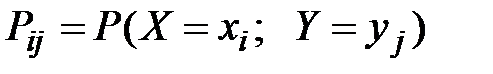 
– вероятность того, что система 
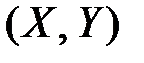примет значения 
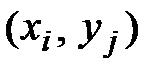, а суммирование распространяется по всем возможным значениям случайных величин 
, 
.
Для непрерывных случайных величин:
; 
,
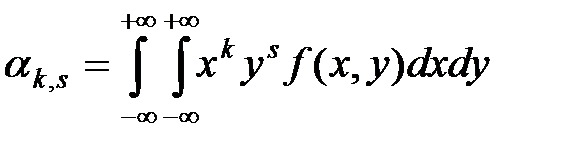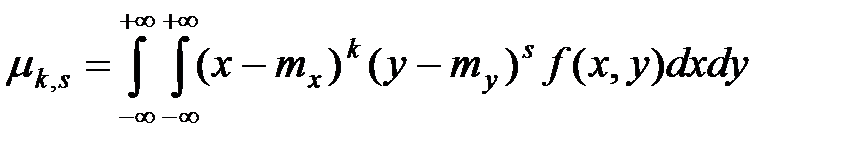где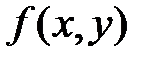 
– плотность распределения системы .
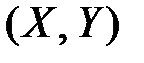Очевидно, что
;
.
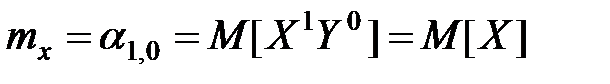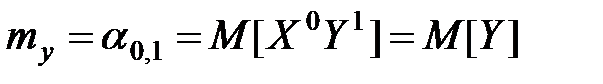Совокупность математических ожидани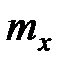й 
и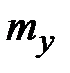 
представляет собой характеристику положения центра системы .
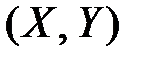Геометрически это координаты средней точки на плоскости (центр тяжести), вокруг которой происходит рассеяние всех точек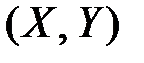 
.
Дисперсии величин Х и Y характеризуют рассеяние случайной точки в направлении осе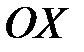й 
и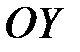 
:
.
.
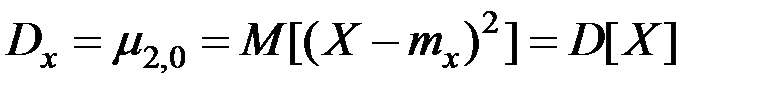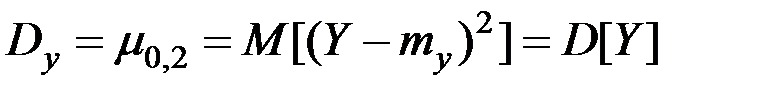Особую роль как характеристики системы играет второй смешанный центральный момент
,
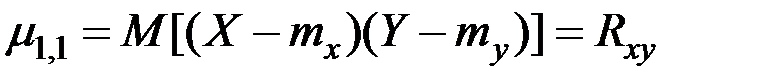т.е. математическое ожидание произведения центрированных величин.
Это ковариационный момент (т.е. момент связи, корреляционный момент) случайных величин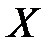 
, 
.
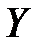Для дискретных случайных величин корреляционный момент выражается формулой
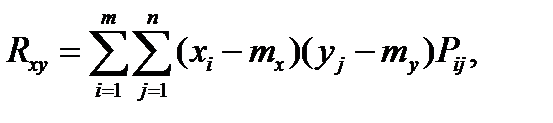
а для непрерывных
.
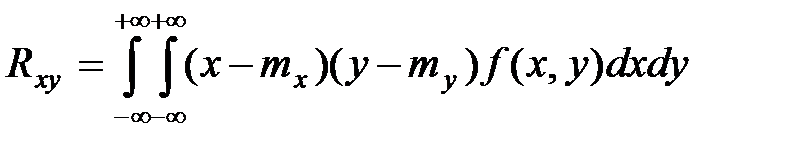Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо рассеяния величин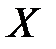 
и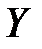 
, ещё и связь между ними. Для независимых случайных величин корреляционный момент равен нулю.
Корреляционный момент характеризует не только зависимость величин, но и их рассеяние. Поэтому для характеристики степени тесноты связи между величинами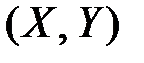 
в чистом виде переходят от момента 
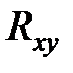к безразмерной характеристике
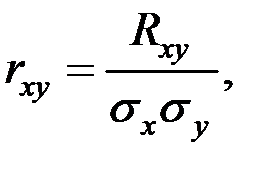
где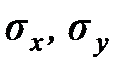 
– средние квадратические отклонения величин 
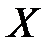и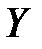 
.
Эта характеристика называется коэффициентом корреляции величин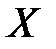 
и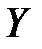 
.
Две независимые случайные величины всегда являются некоррелированными. Обратное верно не всегда. Равенство нулю коэффициента корреляции (корреляционного момента) есть необходимое, но недостаточное условие независимости случайных величин.
Условие независимости случайных величин – более жёсткое, чем условие некоррелированности.
Коэффициент корреляции характеризует степень тесноты только линейной зависимости между случайными величинами.
Свойства коэффициента корреляции:
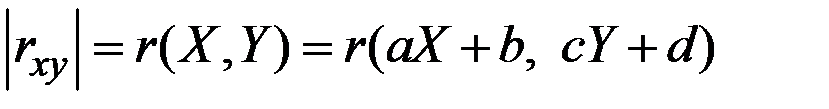, где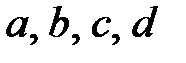 
– константы;
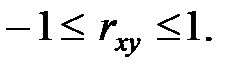
Пример 3.3. Система случайных величин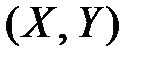 
подчинена закону распределения с плотностью
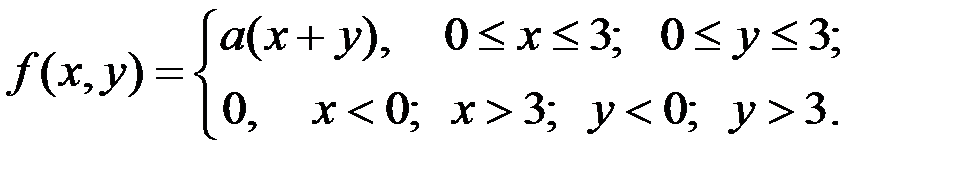
Требуется: определить параметр a; вычислить вероятность попадания точки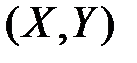 
в прямоугольник, ограниченный прямыми
.
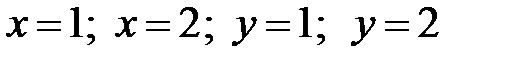Вычислить характеристики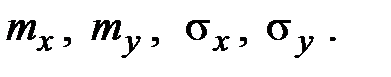 
Решение. Найдём параметр a из уравнения
.
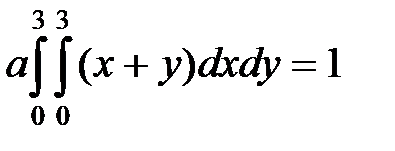Отсюда:
.
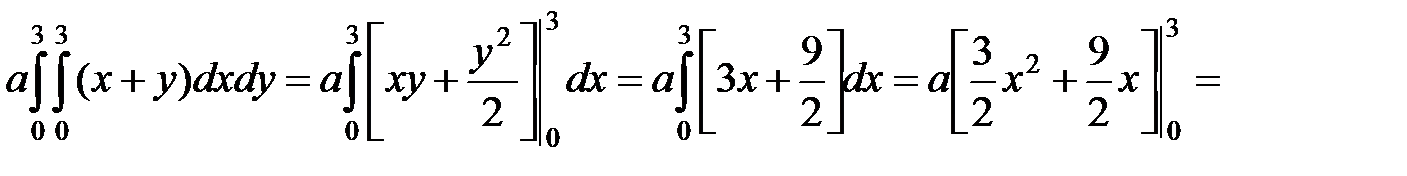
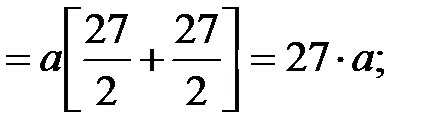
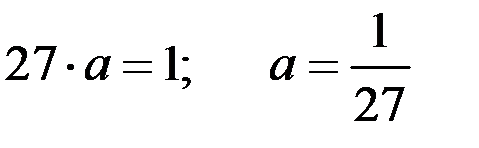Искомая вероятность
.
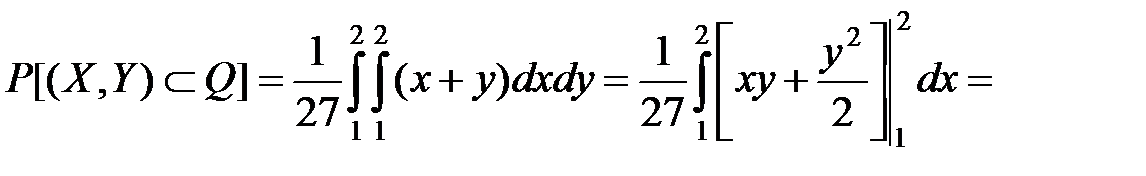
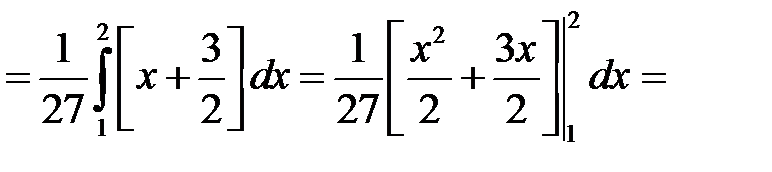
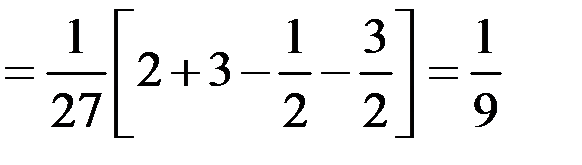По соответствующим формулам вычисляем другие числовые характеристики:
; 
;
.
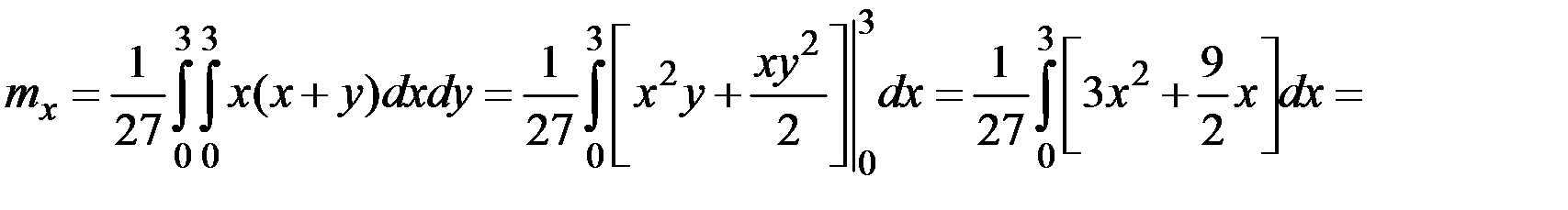
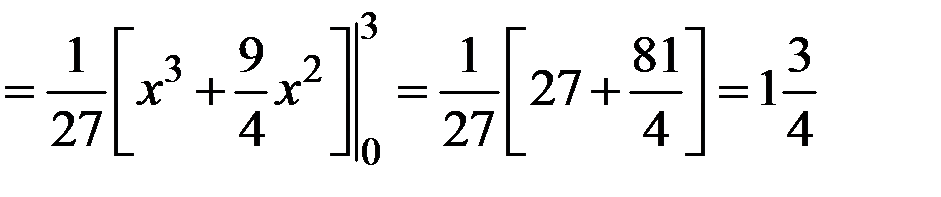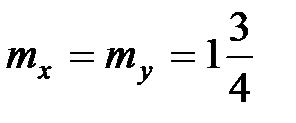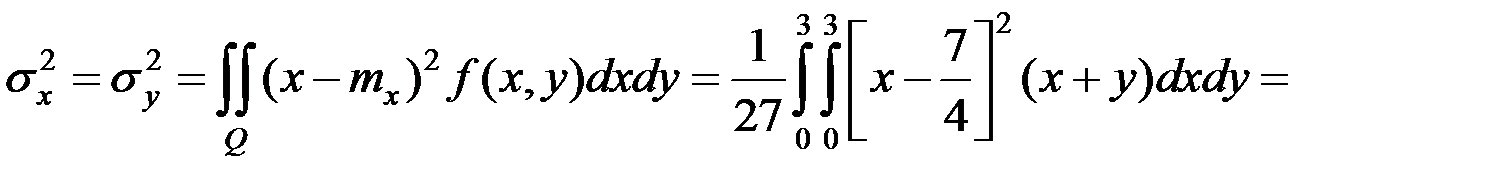
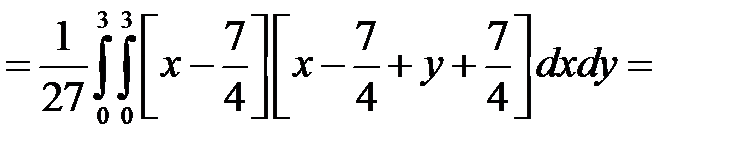
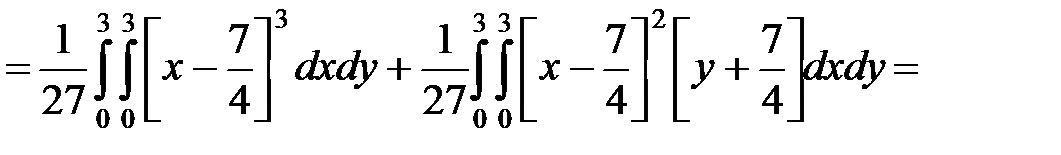
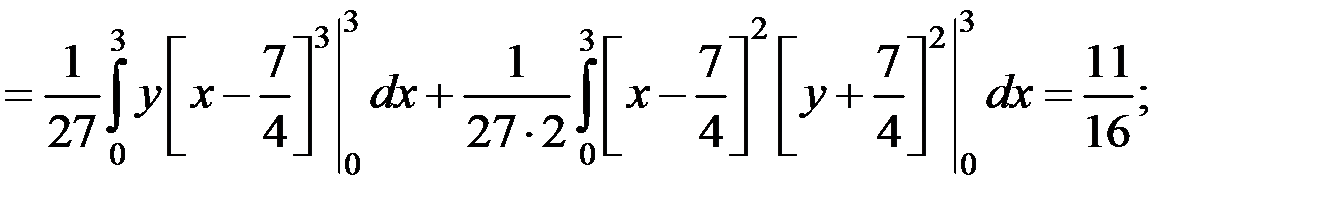
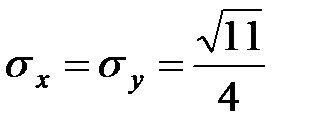Пример 3.4. События А и В имеют одинаковую вероятность p. Какова должна быть условная вероятность Р(А|В), чтобы коэффициент корреляции между А и В был равен числу r.
Решение. Пусть Х = 1 или 0 в зависимости от того, произошло событие А или нет. Пусть Y = 1 или 0 в зависимости от того, произошло событие B или нет. Обозначим P(A|B) = P(B|A) = p1.
Тогда P(AB) = pp1, P( 
B) = p (1 – p1), P( 
) = p(1 – p1), P(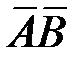 
) = 1 – pp1 – 2p(1– p1) = 1 – 2p + pp1, т.е. совместное распределение (Х,Y) задаётся таблицей:
| Y (В) | ||
| X (А) | 1 | 0 |
| 1 | pp1 | p(1 – p1) |
| 0 | p(1 – p1) | 1 – 2p + pp1 |
Следовательно,
M[X] = M[Y] = p,
D[X] = D[Y] = p(1 – p),
M[XY] = pp1,
Rxy = p(p1 – p),
rxy =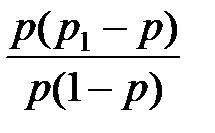 
= r,
т.е.
p1 = P(A|B) = p + r(1 – p).