Задания для контрольной работы № 2
Задание № 2.1. Вероятность досрочного выполнения заказа каждой из N фирм равна P. Определить мат. ожидание, дисперсию и среднее квадратическое отклонение числа фирм, досрочно выполнивших заказ (табл. 2.4).
Задание № 2.2. Среднее число заявок, поступивших от клиентов в банк за А минут, равно N. Найти вероятность того, что за B минут поступит (табл. 2.4): ровно C заявок; 2) не менее C заявок.
Задание № 2.3. Месячная рентабельность производства описывается нормальным законом распределения. Средняя (нормативная) рентабельность составляет m %, а среднее квадратическое отклонение рентабельности составляет s %. Какова вероятность того, что рентабельность производства в текущем месяце будет заключена в пределах от a % до b % (табл. 2.4)?
Таблица 2.4
Варианты заданий № 2.1, 2.2, 2.3
| № варианта | Значения параметров | ||||||||
| N | P | A | B | C | m | s | a | b | |
| 1 | 4 | 0,90 | 10 | 15 | 3 | 20 | 3,1 | 19 | 21 |
| 2 | 5 | 0,80 | 20 | 15 | 4 | 18 | 2,8 | 18 | 25 |
| 3 | 6 | 0,70 | 30 | 10 | 2 | 16 | 2,5 | 10 | 13 |
| 4 | 3 | 0,60 | 4 | 8 | 5 | 22 | 3,2 | 16 | 23 |
| 5 | 4 | 0,40 | 5 | 6 | 3 | 19 | 3,3 | 18 | 20 |
| 6 | 5 | 0,60 | 6 | 8 | 4 | 21 | 4,0 | 20 | 23 |
| 7 | 6 | 0,75 | 7 | 10 | 5 | 23 | 4,1 | 20 | 22 |
| 8 | 3 | 0,85 | 8 | 12 | 2 | 24 | 4,2 | 20 | 25 |
| 9 | 4 | 0,95 | 10 | 18 | 1 | 25 | 5,0 | 24 | 28 |
| 10 | 5 | 0,65 | 5 | 7 | 8 | 20 | 3,8 | 22 | 23 |
| 11 | 6 | 0,90 | 2 | 3 | 9 | 22 | 3,7 | 20 | 25 |
| 12 | 3 | 0,80 | 2 | 4 | 2 | 21 | 2,4 | 17 | 19 |
| 13 | 4 | 0,70 | 5 | 8 | 2 | 19 | 2,6 | 17 | 18 |
| 14 | 5 | 0,60 | 5 | 10 | 3 | 18 | 3,1 | 20 | 22 |
| 15 | 6 | 0,45 | 10 | 8 | 4 | 17 | 2,8 | 19 | 20 |
| 16 | 3 | 0,55 | 10 | 6 | 2 | 16 | 3,3 | 15 | 19 |
| 17 | 4 | 0,35 | 8 | 7 | 3 | 15 | 2,5 | 17 | 22 |
| 18 | 5 | 0,25 | 6 | 3 | 4 | 14 | 2,6 | 13 | 16 |
| 19 | 6 | 0,15 | 7 | 14 | 2 | 13 | 2,2 | 10 | 14 |
| 20 | 3 | 0,10 | 9 | 15 | 5 | 12 | 2,6 | 10 | 15 |
| 21 | 4 | 0,20 | 12 | 10 | 3 | 19 | 2,7 | 17 | 22 |
| 22 | 5 | 0,30 | 4 | 8 | 3 | 22 | 2,8 | 20 | 23 |
| 23 | 6 | 0,40 | 16 | 12 | 3 | 18 | 2,9 | 16 | 21 |
| 24 | 2 | 0,70 | 7 | 21 | 4 | 17 | 2,4 | 16 | 20 |
| 25 | 3 | 0,90 | 8 | 16 | 4 | 28 | 2,6 | 25 | 29 |
| 26 | 5 | 0,65 | 6 | 3 | 2 | 15 | 2,8 | 14 | 28 |
| 27 | 6 | 0,90 | 7 | 4 | 5 | 14 | 2,5 | 12 | 32 |
| 28 | 6 | 0,80 | 8 | 8 | 3 | 13 | 3,2 | 10 | 30 |
| 29 | 3 | 0,70 | 10 | 10 | 4 | 12 | 3,3 | 17 | 19 |
| 30 | 4 | 0,45 | 5 | 8 | 5 | 19 | 4,0 | 17 | 22 |
3. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
3.1. Система двух случайных величин
Часто результат опыта описывается не одной случайной величиной, а двумя или более случайными величинами, образующими систему.
Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных величин, её составляющих: помимо этого, они включают также взаимные связи (зависимости) между случайными величинами.
Система двух случайных величин 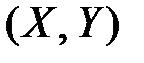 полностью описывается двумерным законом распределения, обычно задаваемым в одной из трёх форм.
полностью описывается двумерным законом распределения, обычно задаваемым в одной из трёх форм.
1. Ряд распределения.
Для системы двух дискретных случайных величин закон распределения удобно задавать в виде прямоугольной таблицы, где по одной стороне откладываются возможные значения одной переменной, по другой – значения второй переменной, а в соответствующих клетках на пересечении столбцов и строк заносятся вероятности совместного появления событий (табл. 3.1).
Таблица 3.1
Ряд распределения системы двух дискретных величин
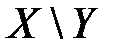
| 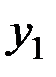
| 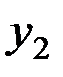
| ... | 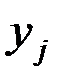
| ... | 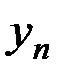
|
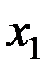
| 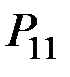
| 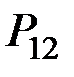
| ... | 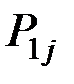
| ... | 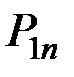
|
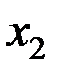
| 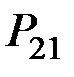
| 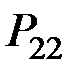
| ... | 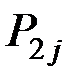
| ... | 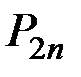
|
| ... | ... | ... | ... | ... | ... | ... |
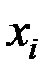
| 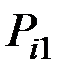
| 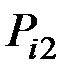
| ... | 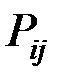
| ... | 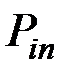
|
| ... | ... | ... | ... | ... | ... | ... |
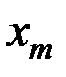
| 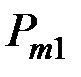
| 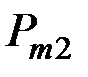
| ... | 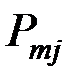
| ... | 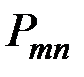
|
Здесь 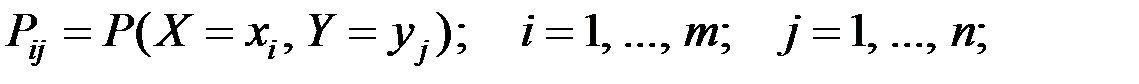
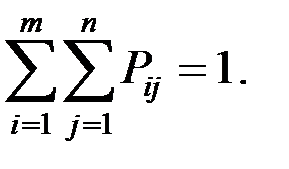
2. Функция распределения.
Функция распределения системы двух СВ 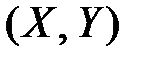 – это вероятность совместного выполнения двух неравенств
– это вероятность совместного выполнения двух неравенств 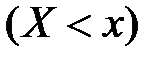 и
и 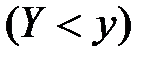 :
:
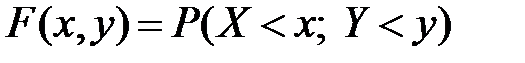 .
.
Геометрически функция 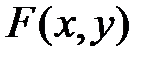 есть вероятность попадания случайной точки
есть вероятность попадания случайной точки 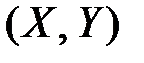 в бесконечный квадрант с вершиной в точке
в бесконечный квадрант с вершиной в точке 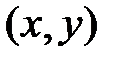 , лежащий левее и ниже значения
, лежащий левее и ниже значения 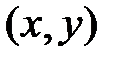 .
.








