Контрольные задачи к разделу 2
2.1. Случайная величина X задана функцией распределения
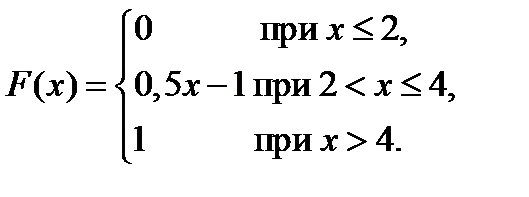
Найти вероятность того, что в результате испытания X примет значения, заключённые в промежутке (2,5; 3,6).
2.2. При каких значениях параметров А и В функция F(x) = A + Be – x может быть функцией распределения для неотрицательных значений случайной величины Х.
2.3. Случайная величина X задана функцией распределения
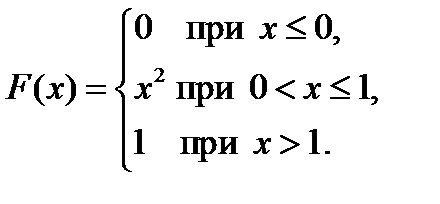
Найти вероятность того, что в результате четырёх независимых испытаний величина X ровно 3 раза примет значение, принадлежащее интервалу (0,25;0,75).
2.4. Вероятность попадания мячом в корзину при одном броске равна 0,3. Составить закон распределения числа попаданий при трёх бросках.
2.5. Два стрелка делают по одному выстрелу в мишень. Вероятность попадания в неё первым стрелком равна 0,5, вторым – 0,4. Составить закон распределения числа попаданий в мишень.
2.6. Испытываются 3 элемента, работающих независимо друг от друга. Длительности времени (в часах) безотказной работы элементов имеют функции плотности распределения: для первого: F1(t) =1-e -0,1t , для второго: F2(t) = 1-e -0,2t , для третьего: F3(t) =1-e -0,3t . Найти вероятность того, что в интервале времени от 0 до 5 часов: откажет только один элемент; откажут только два элемента; откажут все три элемента.
2.7. Дана плотность вероятности f(x) случайной величины X:
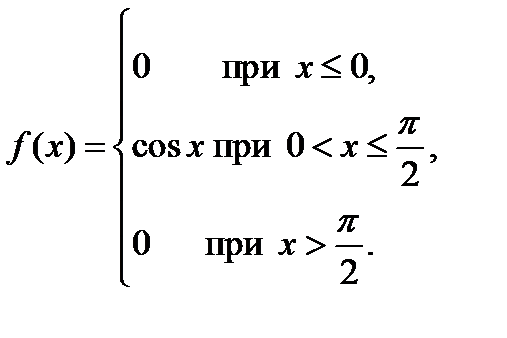
Найти функцию распределения F(x).
2.8. Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.
2.9. В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Составить закон распределения числа стандартных деталей среди отобранных.
2.10. Случайная величина 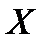 имеет плотность распределения
имеет плотность распределения
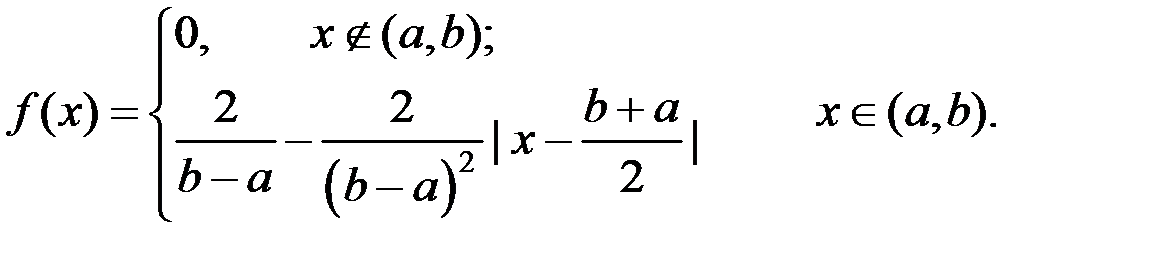
причём 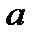 и
и 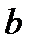 не известны, но
не известны, но 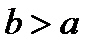 , а
, а 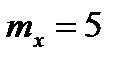 и
и 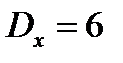 . Найдите
. Найдите 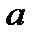 и
и 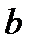 .
.
2.11. В среднем по 10% договоров страховая компания выплачивает страховые суммы в связи с наступлением страхового случая. Вычислить математическое ожидание и дисперсию числа таких договоров среди наудачу выбранных четырёх.
2.12. Из пяти роз две белые. Составить закон распределения случайной величины, выражающей число белых роз среди двух одновременно взятых.
2.13. Среди 15 собранных агрегатов 6 нуждаются в дополнительной смазке. Составить закон распределения числа агрегатов, нуждающихся в дополнительной смазке, среди пяти наудачу выбранных из общего числа.
2.14. Из поступивших в ремонт 10 часов 7 нуждаются в общей чистке механизма. Часы не рассортированы по виду ремонта. Мастер, желая найти часы, нуждающиеся в чистке, рассматривает их поочерёдно и, найдя такие часы, прекращает дальнейший просмотр. Найти математическое ожидание и дисперсию числа просмотренных часов.
2.15. Абонент забыл последнюю цифру нужного ему номера телефона, однако помнит, что она нечётная. Найти математическое ожидание и дисперсию числа сделанных им наборов номера телефона до попадания на нужный номер, если последнюю цифру он набирает наудачу, а набранную цифру в дальнейшем не набирает.
2.16. Вероятность отказа за время испытаний на надёжность для каждого прибора серии равна p. Определить математическое ожидание числа приборов, давших отказ, если испытанию подверглись N приборов.
2.17. Дискретная случайная величина X принимает 3 возможных значения: 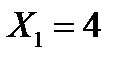 с вероятностью
с вероятностью 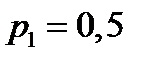 ;
; 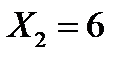 с вероятностью
с вероятностью 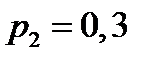 и
и 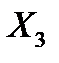 с вероятностью
с вероятностью 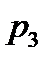 . Найти
. Найти 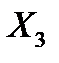 и
и 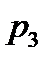 , зная, что M(X) = 8.
, зная, что M(X) = 8.
2.18. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. В каждой партии содержится 5 изделий. Найти математическое ожидание случайной величины X – числа партий, в каждой из которых содержится ровно 4 стандартных изделия, если проверке подлежат 50 партий.
2.19. Найти дисперсию случайной величины X – числа появлений события A в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что M(X) = 0,9.
2.20. Математическое ожидание и среднее квадратическое отклонение нормально распределённой случайной величины X соответственно равны 20 и 5. Найти вероятность того, что в результате испытания X примет значение, заключённое в интервале (15; 25).
2.21. Дана функция: 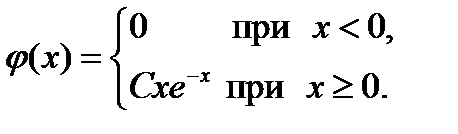
При каком значении параметра C эта функция является плотностью распределения некоторой непрерывной случайной величины X? Найти математическое ожиданий и дисперсию случайной величины X.
2.22. Величина X задана плотностью вероятности 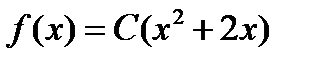 в интервале (0;1), вне этого интервала
в интервале (0;1), вне этого интервала 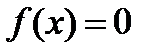 . Найти: постоянный параметр С; математическое ожидание величины X.
. Найти: постоянный параметр С; математическое ожидание величины X.
2.23. Случайная величина X в интервале (0; π) задана плотностью вероятности 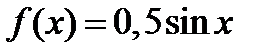 . Вне этого интервала
. Вне этого интервала 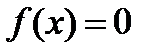 . Найти дисперсию X.
. Найти дисперсию X.
2.24. Устройство состоит из N элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна p. Необходимо найти математическое ожидание и дисперсию этой величины.
2.25. Производится три независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 0.25. Определить среднее квадратическое отклонение числа попаданий при трёх выстрелах.
2.26. Среднее число клиентов, посещающих страховую компанию за 10 мин., равно трём. Найти вероятность того, что в ближайшие 5 минут придёт хотя бы один клиент.
2.27. Среднее время настройки прибора составляет 5 минут и подчинено показательному распределению. Мастер уже потратил 5 минут на настройку очередного прибора. Найти вероятность того, что он затратит ещё не менее трёх минут на настройку этого прибора.
2.28. В отдел заказов в среднем приходит 18 клиентов в час. Найти вероятность того, что за две минуты в отдел заказов придёт хотя бы один клиент.
2.29. Время ожидания заявки в очереди на процессор подчиняется показательному закону распределения со средним значением 20 секунд. Найти вероятность того, что очередная (произвольная) заявка будет ожидать процессор более 35 секунд.
2.30. Группа студентов в количестве 15 человек проводит собрание в зале, в котором 20 рядов по 10 мест в каждом. Каждый студент занимает место в зале случайным образом. Какова вероятность того, что не более трёх человек будут находиться на восьмом месте ряда?
2.31. В партии из 10 деталей имеется 3 нестандартных. Составить закон распределения дискретной случайной величины Х – числа нестандартных деталей среди трёх отобранных и найти её математическое ожидание.
2.32. Непрерывная случайная величина Х распределена по показательному закону с плотностью f(x) = 0,7e -0,7x (x ³ 0). Найти вероятность того, что она примет значения из интервала (2; 6).
2.33. Найти математическое ожидание и дисперсию числа выигрышных лотерейных билетов, если их приобрели 20 штук, а вероятность выигрыша по одному билету равна 0,3.
2.34. Найти дисперсию дискретной случайной величины Х – числа отказов элемента некоторого устройства в десяти независимых опытах, если вероятность отказа элемента в каждом опыте равна 0,15.
2.35. Для какого из указанных интервалов функция sin(x) может являться функцией распределения случайной величины Х: (0; p/2), (0; p)? Найти вероятность попадания случайной величины Х в интервал (p/6; p/2).
2.36. Функция распределения величины Х имеет вид: F(x) =A+Barctg0,5x; – ¥ < X < +¥. Определить: а) постоянные А и В; б) плотность распределения вероятностей f(х); в) 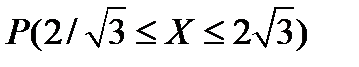 .
.
2.37. Длина изготавливаемой станком–автоматом детали представляет собой случайную величину, распределённую по нормальному закону с параметрами а =15 см, s = 0,2 см. Найти вероятность брака, если допустимые размеры детали должны быть 15 ± 0,3 см. Какую точность длины изготовляемой детали можно гарантировать с вероятностью 0,97?
2.38. Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1. Составить закон распределения числа возвращённых в срок кредитов из 5 выданных. Найти математическое ожидание и этой случайной величины.
2.39. Плотность распределения вероятностей случайной величины Х имеет вид f(x) =A 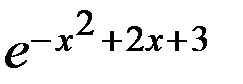 . Найти значение параметра А, М(Х), D(X), функцию распределения F(X), вероятность P(- 1/3 £ X £ 4/3).
. Найти значение параметра А, М(Х), D(X), функцию распределения F(X), вероятность P(- 1/3 £ X £ 4/3).
2.40. Найти дисперсию диаметра втулок, представляющего собой случайную величину, распределённую по нормальному закону, если отклонение от математического ожидания, не превосходящее 0,15 см, имеет место с вероятностью 0,8.
2.41. Имеются 4 ключа, из которых только один подходит к замку. Найти математическое ожидание и дисперсию числа попыток открывания замка, если испробованный ключ в последующих попытках не участвует.
2.42. В отдел заказов в среднем приходит 12 клиентов в час. Определить вероятность того, что за три текущие минуты в отдел заказов придёт хотя бы один клиент.
2.43. Дискретная случайная величина Х принимает значение х1 = 1, х2 = 2, х3 = 3. Известно также М(Х) = 2,3 и М(Х 2) = 5,9. Найти вероятности, соответствующие возможным значениям величины Х.
2.44. При установившемся технологическом процессе 70 % всей производимой продукции станок–автомат выпускает первым сортом, 30 % – вторым. Составить закон распределения числа изделий первого сорта среди 4 изделий, отобранных случайным образом. Найти математическое ожидание и дисперсию рассматриваемой случайной величины.
2.45. Доходы трёх банков от кредитов в отчётном году характеризуются следующими показателями:
| № банка | Средняя процентная ставка, r | Доход банка, тыс. руб., D |
| 1 | 22 | 1800 |
| 2 | 15 | 3400 |
| 3 | 18 | 2800 |
Определить среднюю процентную ставку кредитов банков
2.46. Имеются следующие данные о товарных запасах торгового предприятия (в млн. рублей): 1) на 01.01.2014 г.: 61,1; 2) на 01.05.2014 г.: 57,7; 3) на 01.08.2014 г.: 51,3; 4) на 01.01.2015 г.: 74,7. Определить среднемесячный товарный запас торгового предприятия за 2014 год.
2.47. Первый студент выучил 20 билетов из 50, второй – 30, третий – 40. Студент получает зачёт, если отвечает на вопрос. Найти коэффициент вариации числа студентов (из трёх), сдавших зачёт.
2.48. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,002. Найти вероятность того, что в пути будет повреждено не более трёх изделий.
2.49. Билет на право участия в игре стоит X долларов. Игрок выбрасывает 2 игральные кости и получает выигрыш 150 долларов, если выпали две шестёрки, 12 долларов – при выпадении только одной шестёрки и проигрывает, если ни одной шестёрки не появилось. Какова должна быть минимальная стоимость билетов (целое число), чтобы игра приносила доход её устроителям?
2.50. Число страховых случаев по одному договору в течение года распределено по закону Пуассона. Для половины договоров среднее число страховых случаев в год равно 3, а для другой половины – 5. По случайно взятому договору два года подряд было заявлено по 4 страховых случая в год. Сколько в среднем можно ожидать страховых случаев по этому договору в следующем году?
2.51. 12% договоров из портфеля страховой компании являются договорами с высокой степенью риска, оставшиеся 88% договоров являются договорами с низкой степенью риска. Число страховых случаев по одному договору в течение года распределено по закону Пуассона со средним значением а. Риски, связанные с различными договорами, независимы друг от друга. Для договоров с высокой степенью риска а = 1,3, а для договоров с низкой степенью риска а = 0,4. Сколько в среднем можно ожидать случаев в наступающем году по договору, который в прошлом году привёл к одному страховому случаю?
2.52. Пусть X – CB c плотностью распределения 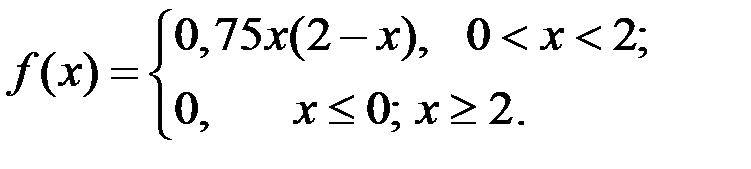
Найти вероятность события 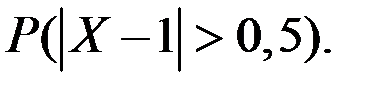
2.53. Завод отправил на базу 200 изделий. Вероятность повреждения изделия в пути 0,005. Найти вероятность того, что в пути будет повреждено не более трёх изделий.








