Пусть СВ Х имеет функцию распределения , заданную по всей числовой оси. Выберем на этой оси интересующий нас отрезок (может быть ).
Распределение СВ Х со значениями, принадлежащими только рассматриваемому отрезку, называется усечённым.
Функция распределения усечённого закона выражается через исходную соотношением
.
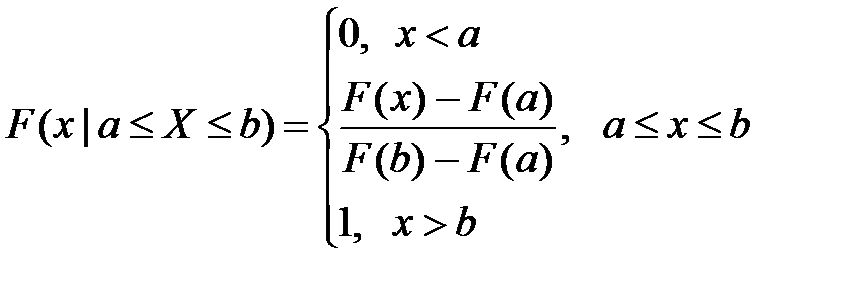Функция плотности усечённого распределения выражается через исходную соотношением
.
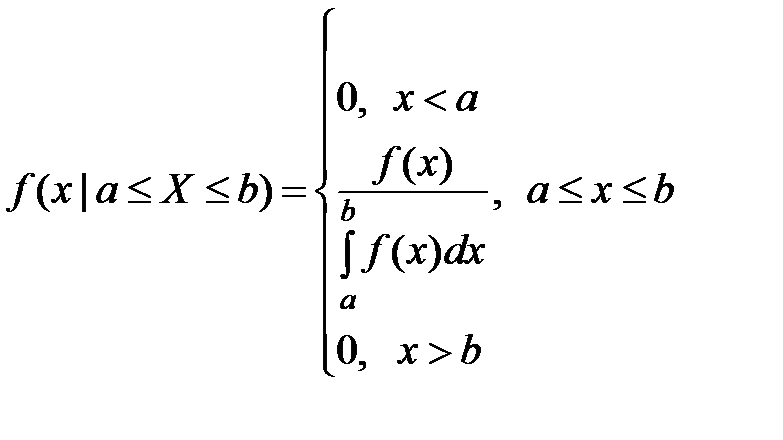Для дискретных СВ интеграл можно заменить соответствующей суммой.
Примечание. Подчеркнём, что многие законы взаимосвязаны (наиболее часто встречающиеся на практике) и при определённых условиях переходят друг в друга.
Пример 2.11. Среднее время настройки прибора составляет 4 минуты и подчинено показательному распределению. Мастер уже потратил 4 минуты на настройку очередного прибора. Найти вероятность того, что он затратит ещё не менее двух минут на настройку этого прибора.
Решение. Имеем закон распределения времени настройки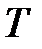 
прибора в виде
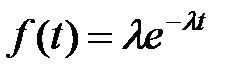, где 
.
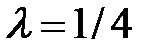С учётом того фактора, что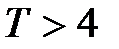 
, имеем усечённое показательное распределение в виде
,
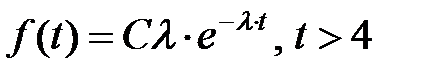где параметр C определяется из соотношения
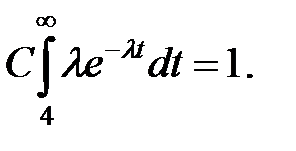
Для нашего случая
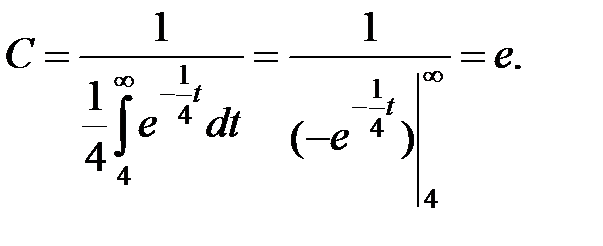
Получаем усечённое распределение в виде
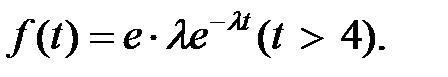
Тогда искомую вероятность найдём по соотношению
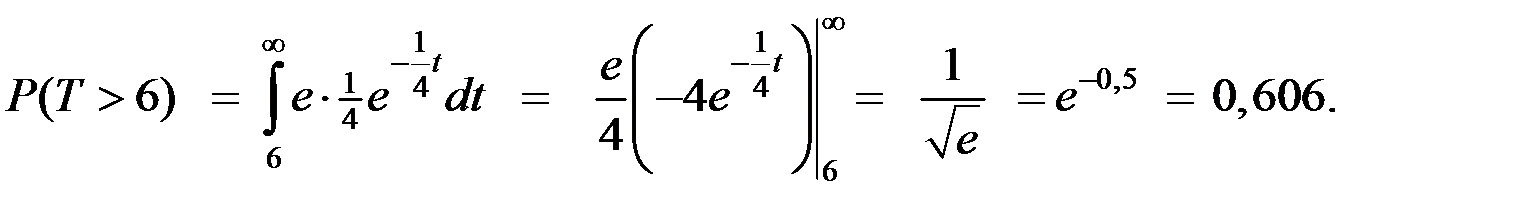
2.4. Решение типовых задач главы 2
Пример 2.12. Пусть X – CB c плотностью распределения
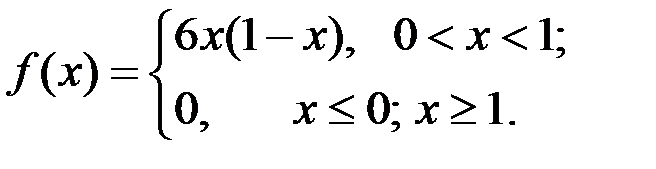
Найти вероятность события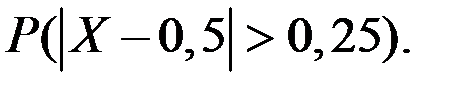 
Решение.
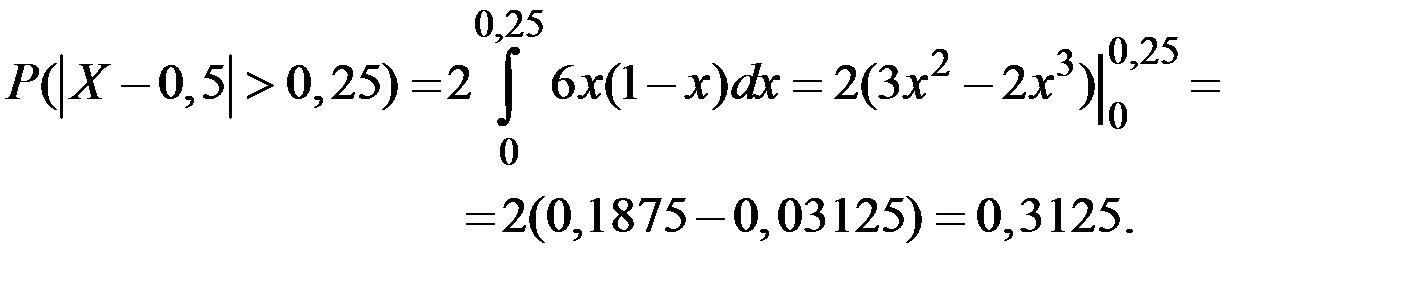
Пример 2.13. Рабочий обслуживает n однотипных станков, расположенных в ряд. Расстояние между станками равно а.
Закончив обслуживание какого–либо станка, рабочий переходит к тому станку, который раньше других потребовал его внимания (подналадка, замена инструмента и т.д.).
Найти среднее значение длины L перехода рабочего, если обслуживать одновременно m рядов (по n станков в каждом), расстояние между которыми равно b.
Решение. Рабочий с вероятностью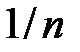 
может в данный момент находиться у одного из станков (в случае одного ряда).
Находясь у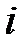 
–го станка, рабочий может с одинаковой вероятностью 
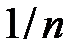проделать путь 
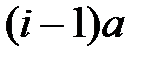до первого станка, путь 
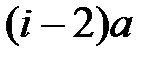до второго, ..., 
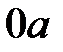до того, у которого стоит, ..., путь 
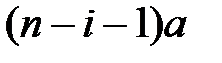до последнего n–го станка.
Тогда:
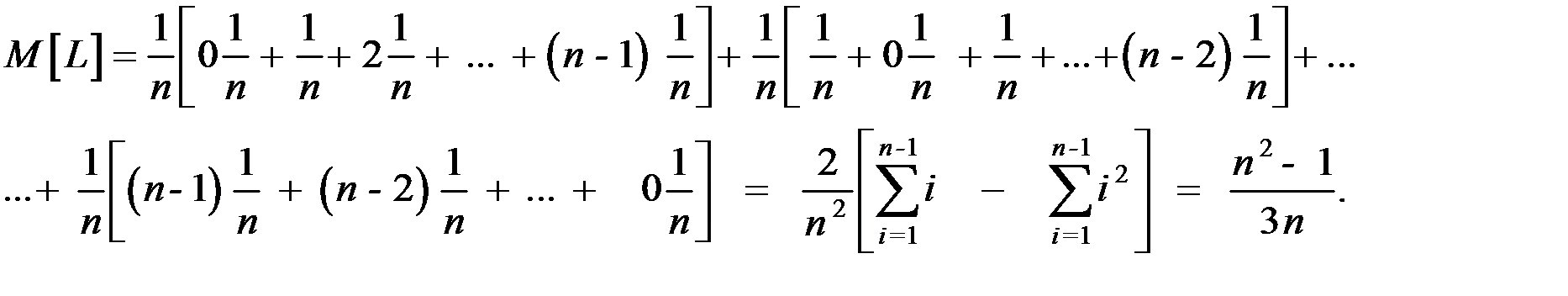
При обслуживании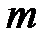 
рядов путь рабочего будет состоять из двух слагаемых: 
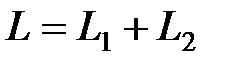, где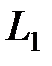 
– путь рабочего вдоль рядов; 
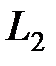– поперёк рядов.
Тогда: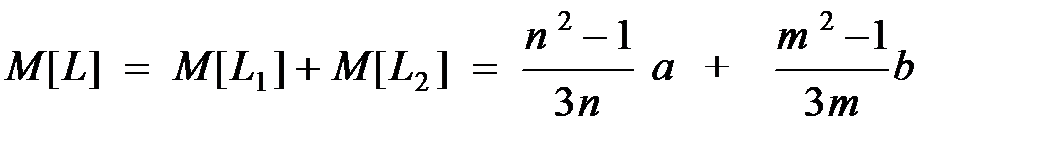 
.
Пример 2.14. Вероятность приёма сигнала одной радиостанции другой радиостанцией равна 0,2 при каждой попытке. Позывные сигналы подаются каждые 5 секунд до тех пор, пока не будет получен ответный сигнал. Общее время прохождения позывного и ответного сигналов равно 16 секунд. Найти среднее число подаваемых сигналов до установления двусторонней связи.
Решение. Вероятность того, что ответный сигнал будет получен на первый позывной равна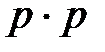 
, на второй – 
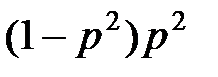, на третий – 
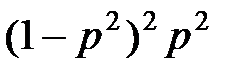…, на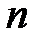 
–й позывной сигнал – 
.
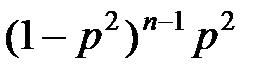Вероятность 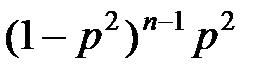означает, что первые 
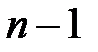позывных сигналов приёмной радиостанцией не приняты, а принят 
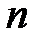–й позывной сигнал и получен ответный сигнал. В этом случае средний номер подаваемого сигнала до установления связи будет равен величине
.
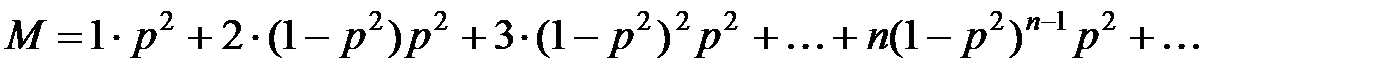С учётом задержки в 3 сигнала среднее число подаваемых сигналов до установления двусторонней связи будет равно
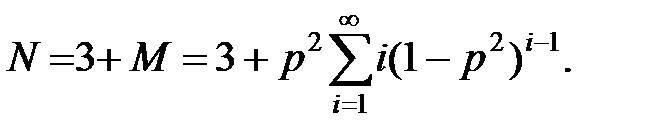
Найдём сумму этого ряда.
Воспользовавшись формулой суммы членов геометрической прогрессии, имеем: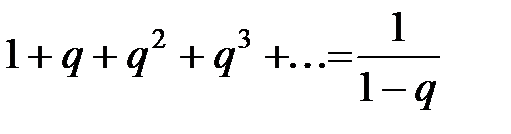 
.
Продифференцировав этот ряд, получим
.
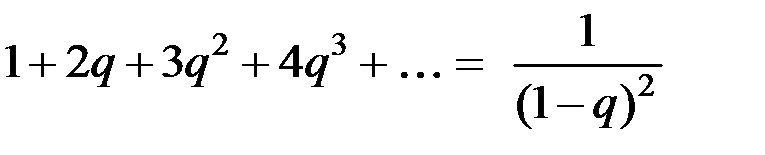Отсюда для случая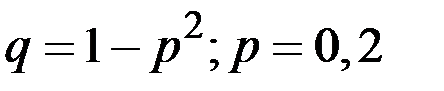 
получаем
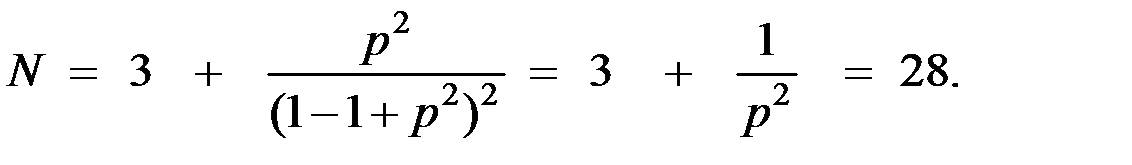
Пример 2.15. Случайная величина ущерба Х распределена по показательному (экспоненциальному) закону со средним значением 250. Определить медиану распределения величины Х.
Решение. Имеем: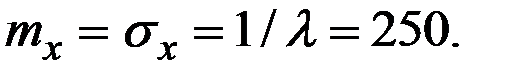 
Параметр показательного закона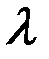 
= 1/250 = 0,004.
Медиана определяется из уравнения
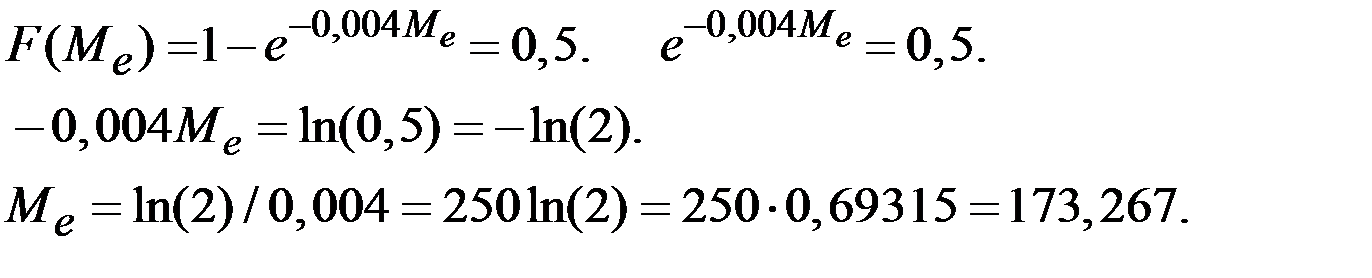
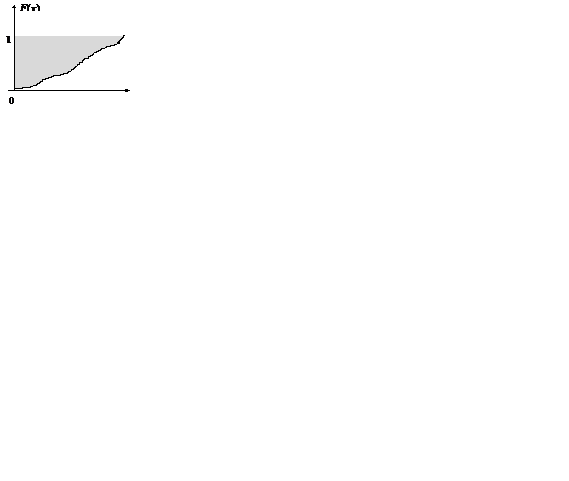
Пример 2.16. Функция распределения F(x) неотрицательной случайной величины X задана графиком.
Математическое ожидание СВ X равно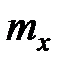 
.
| х |
Показать, что 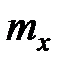геометрически может быть представлено площадью фигуры, заштрихованной на рисунке (ограниченной кривой y = F(x), прямой y = 1 и осью ординат).
Решение.
Из определения математического ожидания имеем
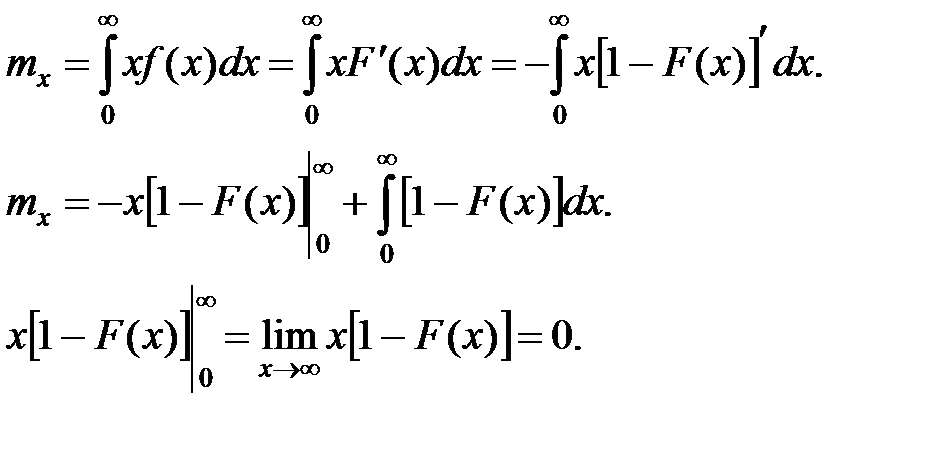
Для СВ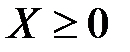 
, имеющей конечное 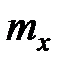, из сходимости интеграла
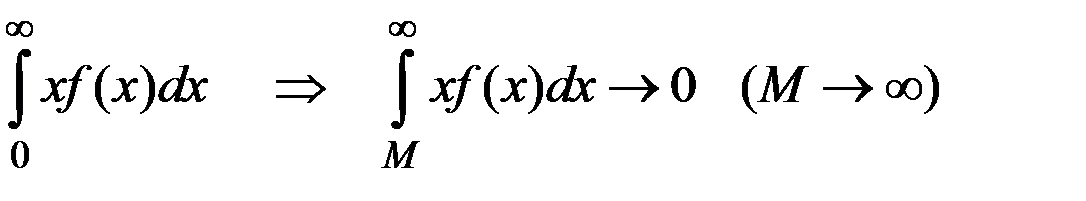
и условия
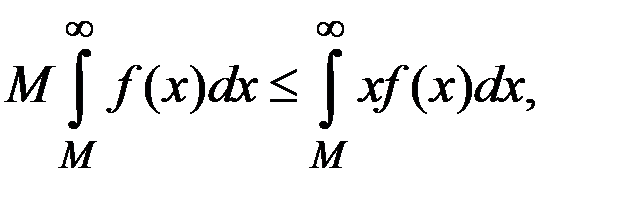
следует, что
,
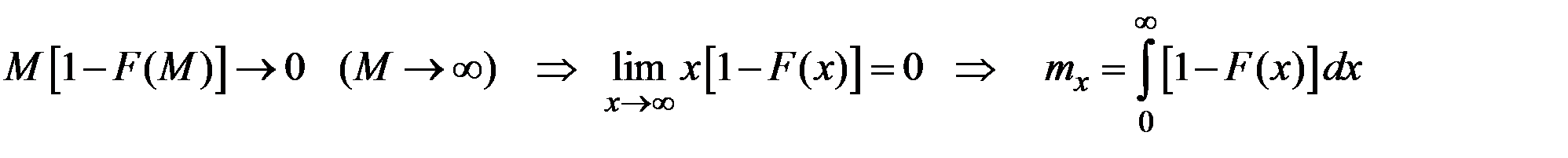а это и есть площадь, заштрихованная на рисунке.
Пример 2.17. Двум первым посетителям страховой компании, имеющим с ней договор, будет вручён памятный подарок в юбилейный для компании день. Вероятность p того, что посетитель страховой компании уже имеет с ней некоторый договор, равна 1/3.
Найти функцию распределения и математическое ожидание числа посетителей до вручения второго памятного подарка.
Решение. Случайная величина Х – количество обслуженных посетителей до вручения двух подарков – может принимать значения 2, 3, 4, ј, i, ј с вероятностями
P(Х = i) = (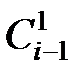 
)р(1 – p)i–2p = (i – 1)p2(1 – p)i–2 = (i – 1)(1/3)2(2/3)i–2.
Это выражение означает, что из первых (i – 1) посетителей один имеет договор и, следовательно, получит подарок, а второй подарок будет вручён i–му посетителю, имеющему договор.
Тогда
mx =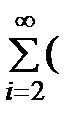 
i–1)Чp2(1–p)i–2 = 2p2 + 3Ч2Чp2q + 4Ч3Чp2q2 + 5Ч4Чp2q3 + ј = p2(2 + 3Ч2Чq + 4Ч3Чq2 + +5Ч4Чq3 + ј) = p2Ч(2q + 3q2 + 4q3 + 5q4 + ј)ў = p2Ч(q2 + q3 + q4 + q5 + ј)ўў = p 
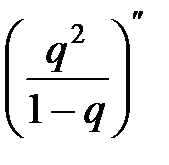= p2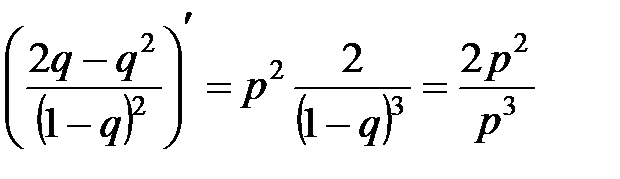 
= 2/p, где q = 1 – p.
При р = 1/3 получим, что mx = 6, то есть в среднем нужно обслужить 6 первых посетителей компании, чтобы двоим вручить соответствующий подарок.
Определим функцию распределения F(x):
при x Ј 2 : F(x) = 0;
при 2 < x Ј 3 : F(x) = (1/3)2;
при 3 < x Ј4 : F(x) = (1/3) 2 +2(1/3) 2(2/3) = (7/3)(1/3) 2 ;ј
јјјјјјјјјј
при i < x Ј i + 1 : F(x) = (1/3)2(1 + 2(2/3) + 3(2/3) 2 + ј + (i–1)(2/3) i–2).
Найдём сумму следующего вида
1 + 2q + 3q2 + 4q3 +ј+ (i–1)qi–2 = (q + q2 + q3 + ј + qi–1)ў =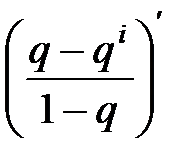 
=
= 
.
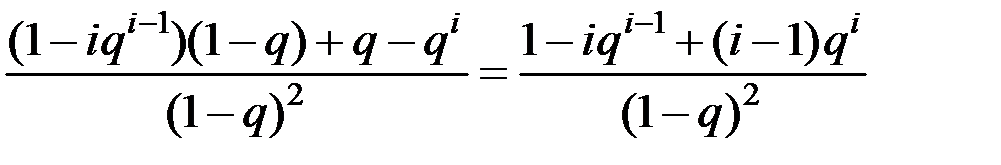При q = 2/3 получаем, что
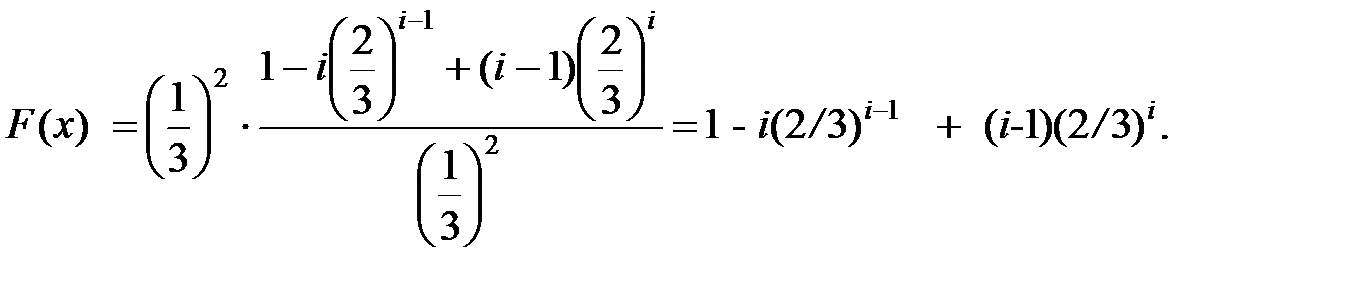
Следовательно, F(x) =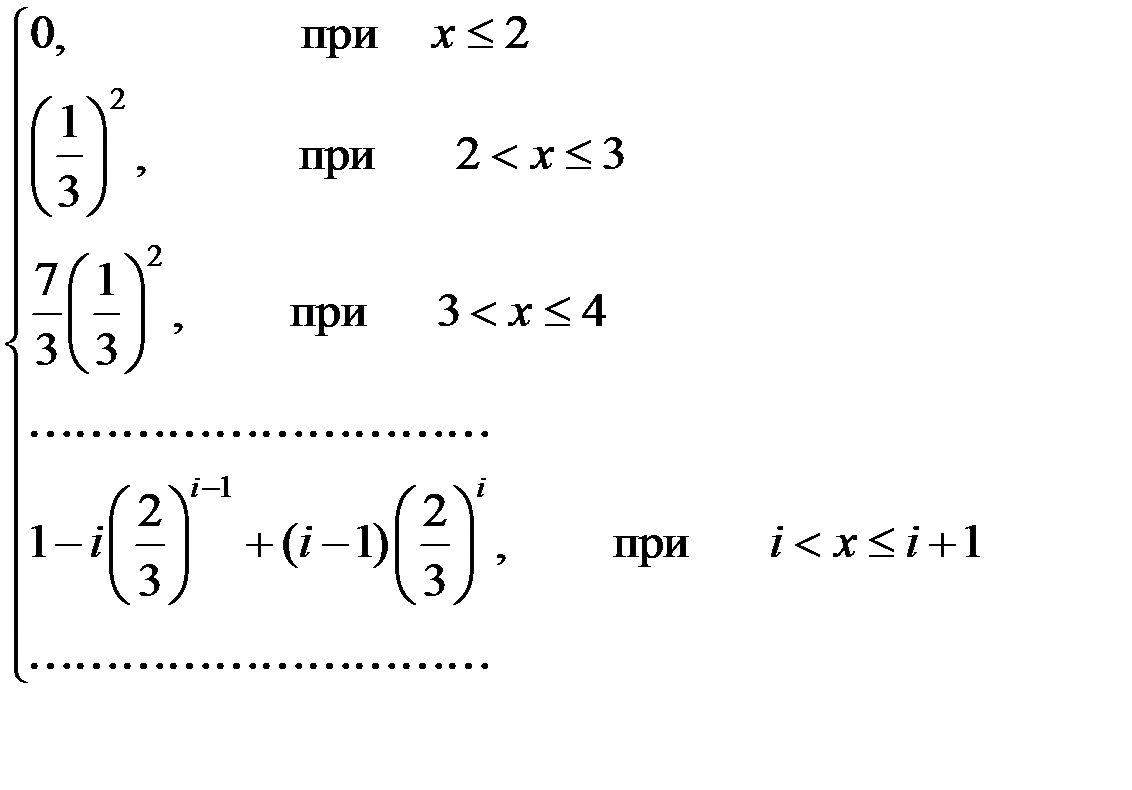 
При х ® Ґ, i ® Ґ : F(x) ® 1.
Пример 2.18. Имеются следующие данные о товарных запасах торгового предприятия (в млн. рублей): 1) на 01.01.2014 г.: 61,1; 2) на 01.05.2014 г.: 57,7; 3) на 01.08.2014 г.: 51,3; 4) на 01.01.2015 г.: 74,7. Определить среднемесячный товарный запас торгового предприятия за 2014 год.
Решение. По условию задачи имеем моментный ряд динамики с неравными интервалами. Поэтому среднемесячный товарный запас торгового предприятия за 2014 год рассчитаем по формуле средней хронологической с неравными интервалами:
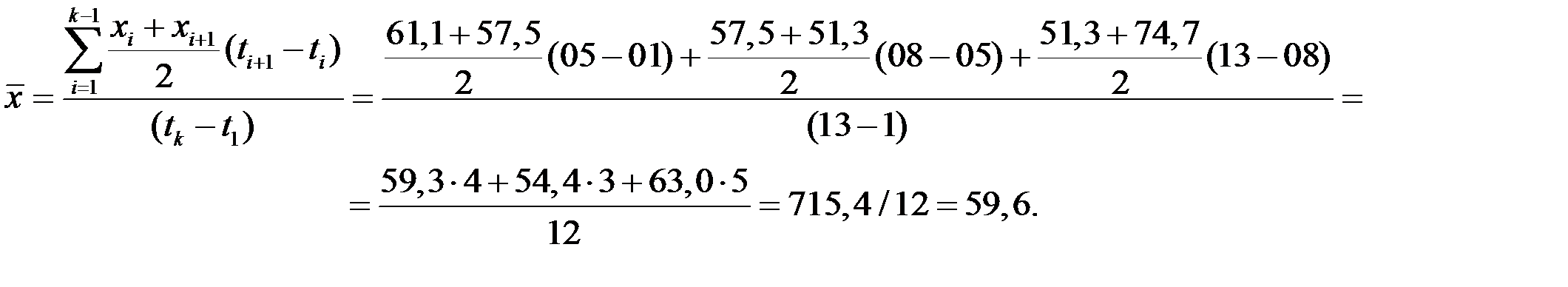
Пример 2.19. Время от момента приобретения оборудования до момента его отказа имеет экспоненциальное распределение со средним значением 10 лет. Владелец оборудования решил застраховать его на случай раннего отказа. По условиям договора страховая компания выплачивает определённую страховую сумму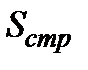 
в случае отказа в течение первого года эксплуатации, 50% от этой суммы в случае отказа в течение второго и третьего первого года эксплуатации и не платит ничего, если оборудование проработает без отказа три года. Известно, что ожидаемые выплаты (математическое ожидание) по этому договору составляют 1000 долларов. Найти размер страховой суммы .
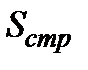Решение. При экспоненциальном распределении времени до отказа:
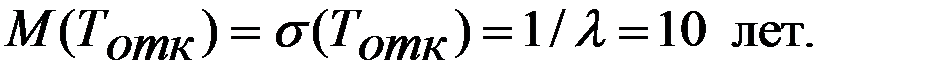
Параметр показательного закона 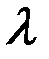= 1/10 = 0,1.
Выплаты страховщика можно выразить следующим образом:
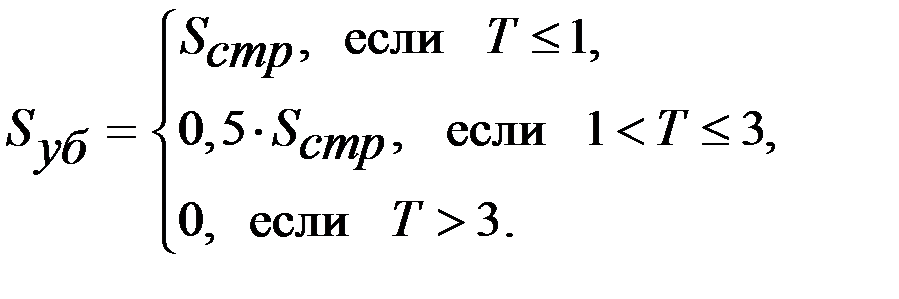
Поэтому
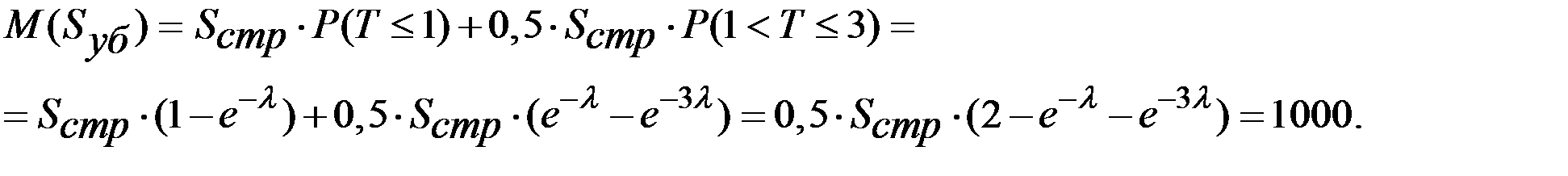
Отсюда для страховой суммы 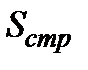имеем:
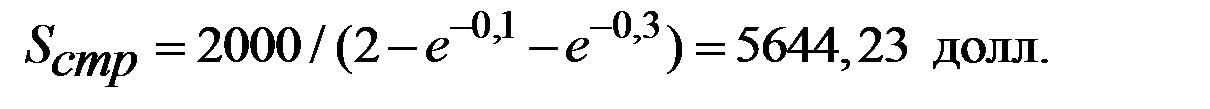
Пример 2.20. Величина ущерба по договорам автомобильного страхования имеет экспоненциальное распределение, а вероятность того, что ущерб меньше 1000 долларов, равна 0,25. Прошло 10 лет. Частота аварий и их характер не изменились, но из–за инфляции ущерб после аварии вырос в два раза по сравнению с ущербом после аналогичной аварии 10 лет назад. Найти вероятность того, что в настоящее время ущерб меньше 1000 долларов.
Решение. Пусть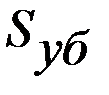 
– размер ущерба после аварии 10 лет назад, а 
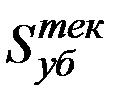– размер ущерба после аварии в настоящее время. Инфляция проявляется в том, что величина 
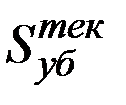/2 распределена так же как и 
.
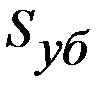Поэтому для искомой вероятности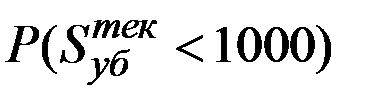 
имеем:
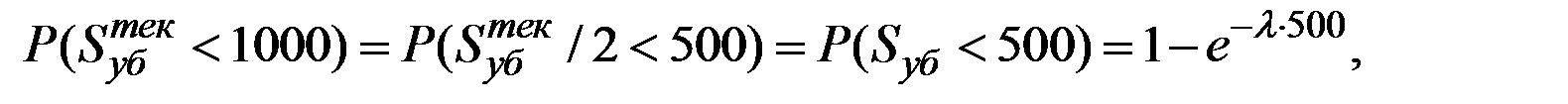
где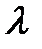 
– параметр экспоненциальной величины 
.
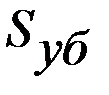По условию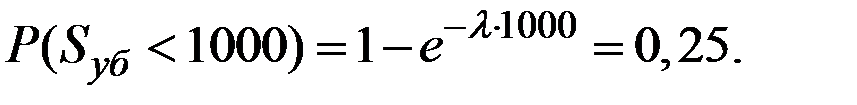 
Формулу для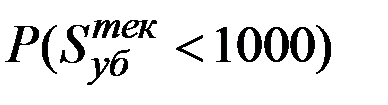 
можно преобразовать так:
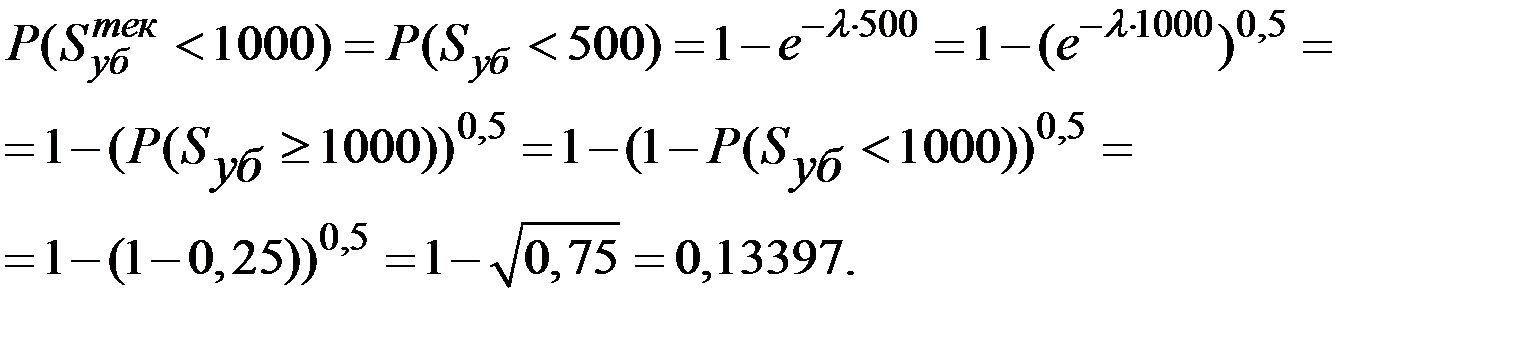
Пример 2.21. 10% договоров из портфеля страховой компании являются договорами с высокой степенью риска, оставшиеся 90% договоров являются договорами с низкой степенью риска. Число страховых случаев по одному договору в течение года распределено по закону Пуассона со средним значением а. Риски, связанные с различными договорами, независимы друг от друга. Для договоров с высокой степенью риска а = 0,6, а для договоров с низкой степенью риска а = 0,1. Сколько в среднем можно ожидать случаев в наступающем году по договору, который в прошлом году привёл к одному страховому случаю?
Решение. Введём обозначения:
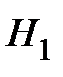– гипотеза: договор имеет высокую степенью риска;
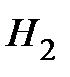– гипотеза: договор имеет низкую степенью риска;
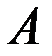– событие: договор привёл к одному страховому случаю.
По условию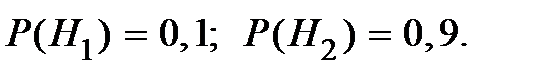 
По формуле Байеса подсчитаем апостериорную вероятность того, что договор, который в прошлом году привёл к одному страховому случаю, имеет высокую степенью риска
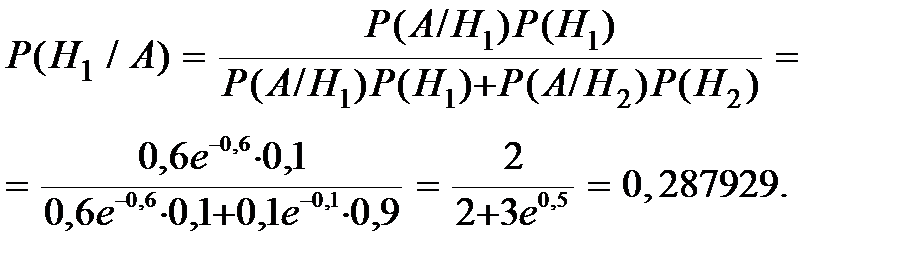
При условии, что договор имеет высокую степенью риска ожидаемое число страховых случаев в наступающем году равно 0,6.
Апостериорную вероятность того, что договор имеет низкую степенью риска
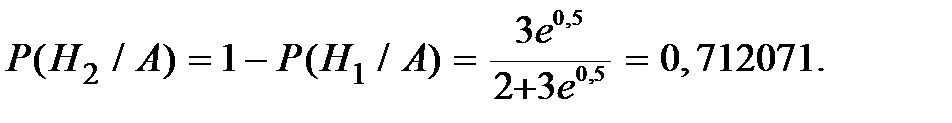
При условии, что договор имеет низкую степенью риска ожидаемое число страховых случаев в наступающем году равно 0,1.
Отсюда в среднем можно ожидать случаев в наступающем году по договору, который в прошлом году привёл к одному страховому случаю
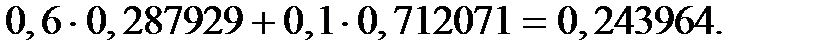
Пример 2.22. Каковы должны быть параметры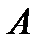 
и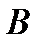 
, чтобы функция 
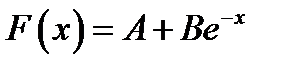являлась бы функцией распределения для 
?
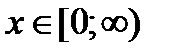Решение. Имеем условия: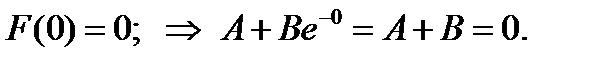 
Тогда
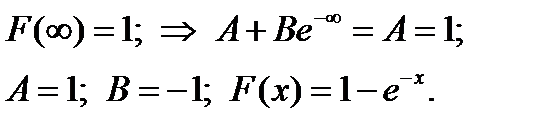
Пример 2.23. Число страховых случаев по одному договору в течение года распределено по закону Пуассона. Для половины договоров среднее число страховых случаев в год равно 2, а для другой половины – 4. По случайно взятому договору два года подряд было заявлено по 4 страховых случая в год. Сколько в среднем можно ожидать страховых случаев по этому договору в следующем году?
Решение. Введём обозначения:
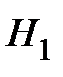– гипотеза: договор имеет в среднем 2 страховых случая в год;
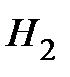– гипотеза: договор имеет в среднем 4 страховых случая в год;
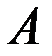– событие: договор привёл два раза подряд к 4 страховым случаям.
По условию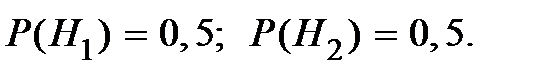 
Считаем, что риски в различные годы независимы и распределены по закону Пуассона: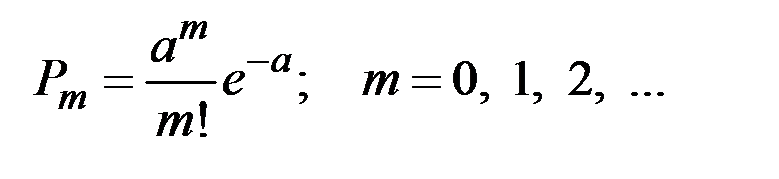 
Имеем среднее число страховых случаев в год: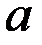 
= 2 для гипотезы 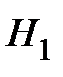и 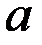= 4 для гипотезы .
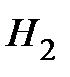Вероятности двукратных четырёх страховых случаев ежегодно для различных гипотез:
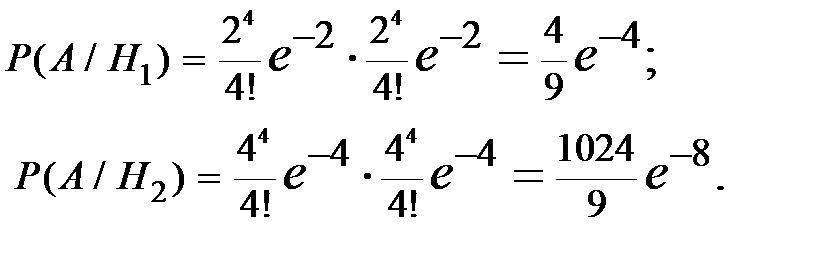
По формуле Байеса подсчитаем апостериорную вероятность того, что договор входит в первую группу
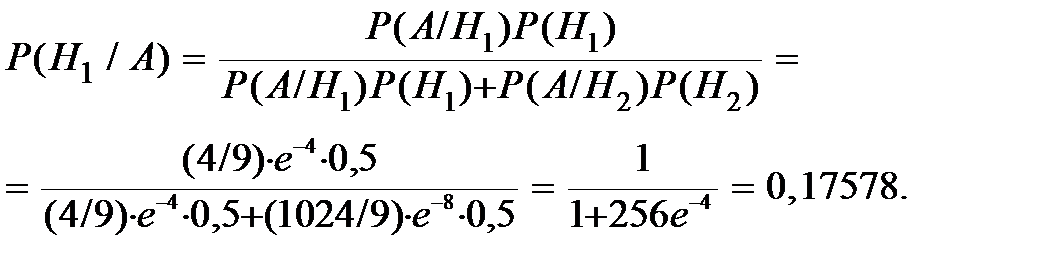
Апостериорную вероятность того, что договор входит во вторую группу
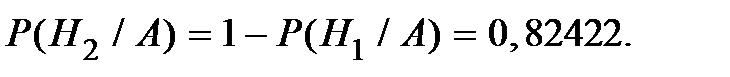
Отсюда в среднем можно ожидать случаев в наступающем году по договору, который привёл два года подряд к 4 страховым случаям в год, равно:
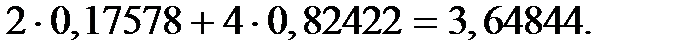
Пример 2.24. Вероятность выпадения зелёного цвета (наступления события А) в одном опыте равна p. Если зелёный цвет выпадает подряд n раз (удачная серия из n опытов), то игрок получает y n рублей; если же n = 0, то он платит 1 долл. за эту попытку. Найти величину y так, чтобы игра была безобидной (мат. ожидание проигрыша равнялось бы нулю).
Решение. Пусть X – выигрыш. Возможные значения величины X в серии: – 1, y, y 2, …, y n…
Имеем ряд распределения выигрыша:
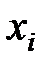
| – 1 | у | y 2 | … | y n | … |
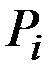
| 1 – р | р(1 – р) | р2(1 – р) | … | р n(1 – р) | … |
Тогда:
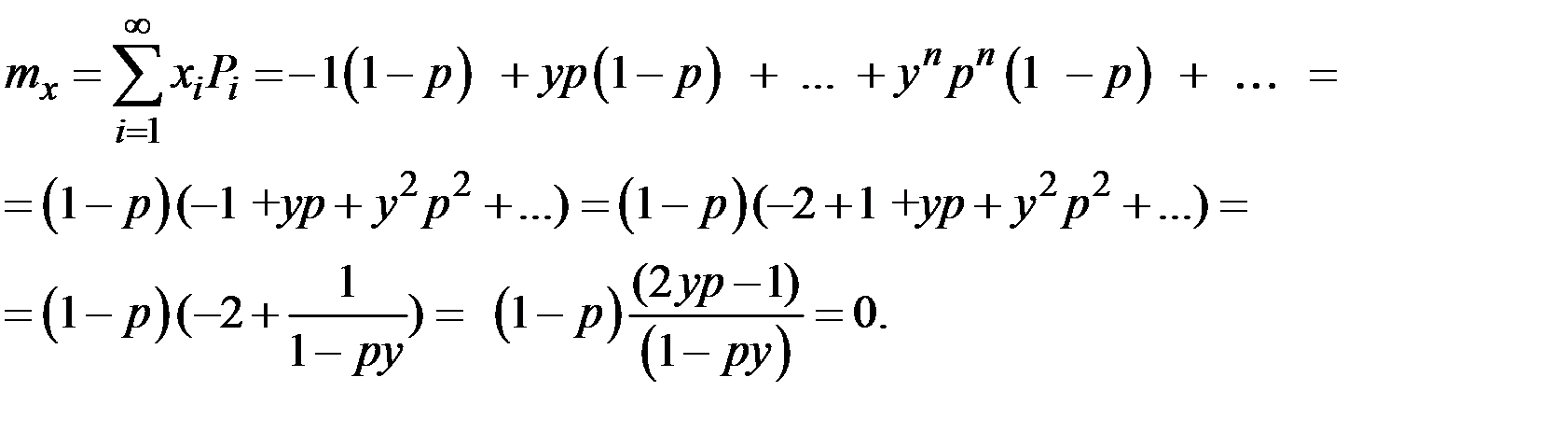
Следовательно,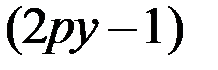 
=0. Отсюда: у = 1/(2р).
Пример 2.25. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,002. Найти вероятность того, что в пути будет повреждено не более трёх изделий.
Решение. В среднем в пути будет повреждено 500 
0,002 = 1 изделие.
Имеем закон Пуассона с параметром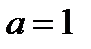 
. 
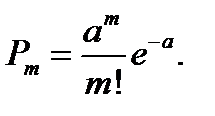
Для различных m получаем:
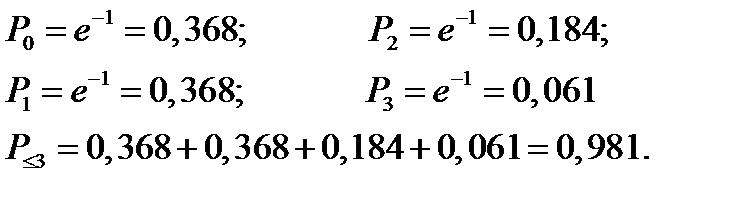
Пример 2.26. Производится стрельба до первого попадания по цели. Вероятность попадания в цель при одном выстреле 0,6. Найти вероятность того, что попадание произойдёт при третьем выстреле.
Решение. Имеем геометрическое распределение.
Пусть Х – число испытаний, которое нужно провести до первого появления события А, вероятность которого в одном опыте равна Р = 0,6.
Тогда для k = 3 получаем
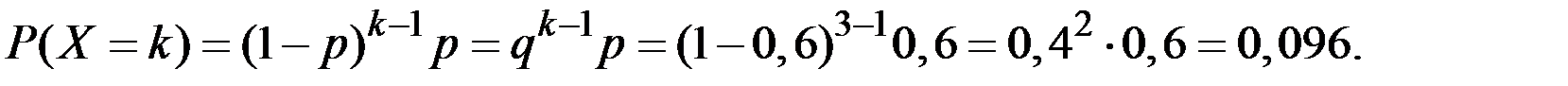
Пример 2.27. Поштучно проверяются изделия, каждое из которых независимо от других может с вероятностью Р = 0,3 оказаться дефектным. Найти математическое ожидание бездефектных изделий между двумя дефектными.
Решение. Имеем геометрическое распределение (k – число неудач до первого успеха).
Пусть Х – число испытаний, которое нужно провести до первого появления события А, вероятность которого в одном опыте равна Р = 0,3.
Тогда получаем
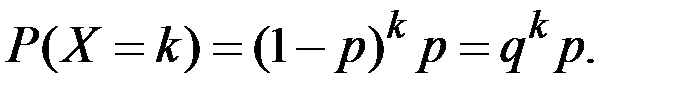
При этом имеем параметры закона:
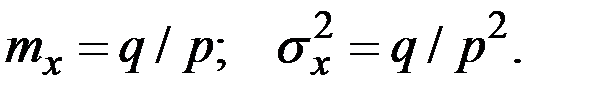
Тогда
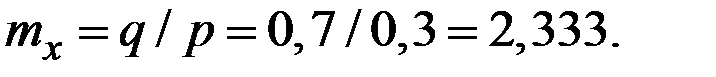
Пример 2.28. Вероятность того, что некоторая машина сломается в любой конкретный день равна 0,2, и это событие не зависит от происходящего в другие дни. Машина может ломаться только один раз в день. Найти вероятность того, что машина сломается два или более раз в течение десяти дней.
Решение. Используем два способа вычисления этой вероятности: по формуле закона Пуассона и по формуле Бернулли.
1. Используем формулу Бернулли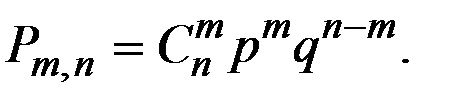 
Получим:
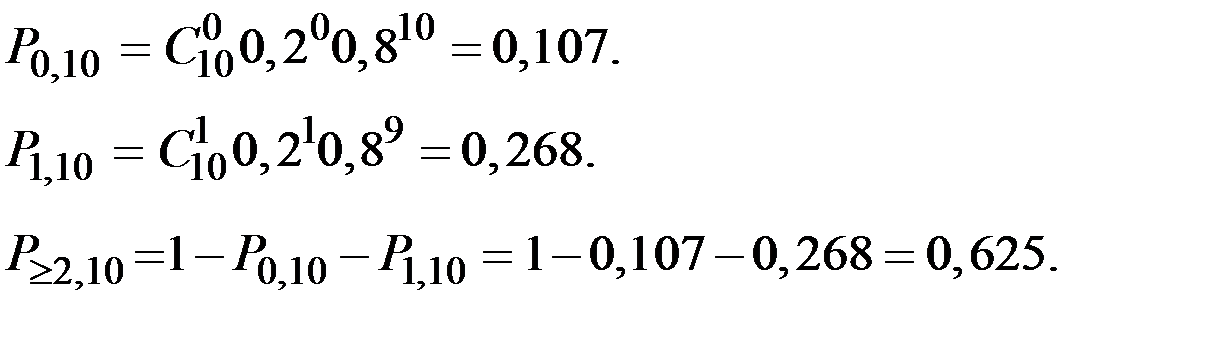
1. Используем формулу закона Пуассона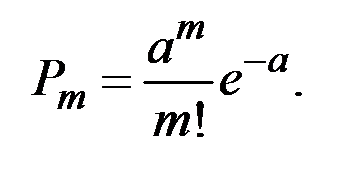 
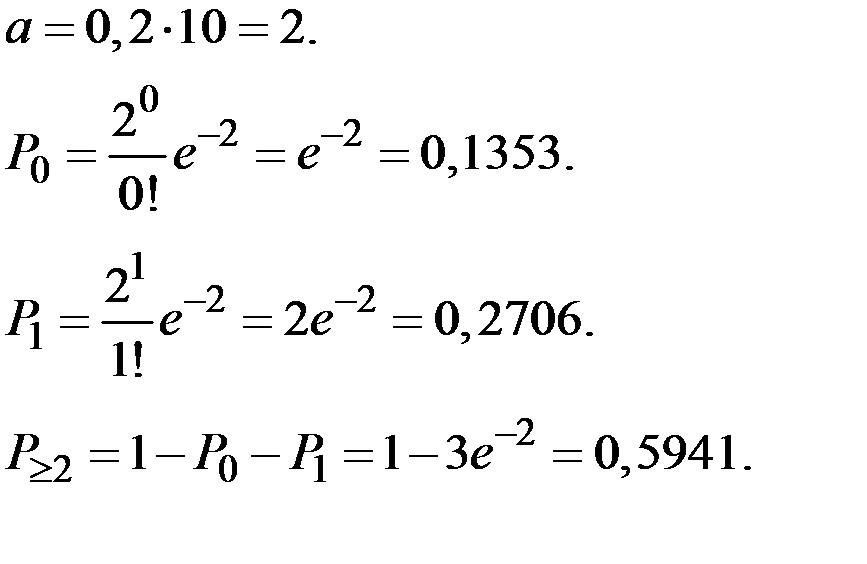
Пример 2.29. При сборке механизма для наиболее точной подгонки основной детали может потребоваться 1, 2, 3, 4 или 5 проб в зависимости от сортности деталей, поступающих на сборку. На одну пробу затрачивается 1 мин., а доли сортностей деталей, поступающих на сборку, составляют от 0,07, 0,21, 0,55, 0,16, 0,01. Определить среднее время, необходимое для установки основной детали в 30 механизмах.
Решение. Имеем распределение числа проб (попыток) Х:
| Число проб Х | 1 | 2 | 3 | 4 | 5 |
| Доля Р (вероятность) | 0,07 | 0,21 | 0,55 | 0,16 | 0,01 |
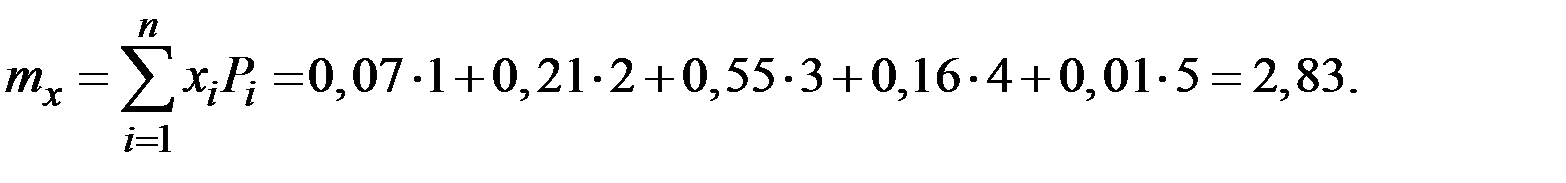
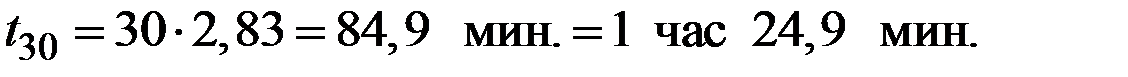
Пример 2.30. В наблюдениях Резерфорда и Гейгера радиоактивное вещество за промежуток времени в 7,5 секунд испускало в среднем 3,87 α–частицы. Найти вероятность того, что за одну секунду это вещество испустит хотя бы одну α–частицу.
Решение. Используем формулу закона Пуассона .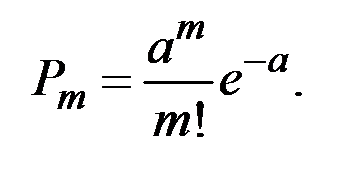
Получим:
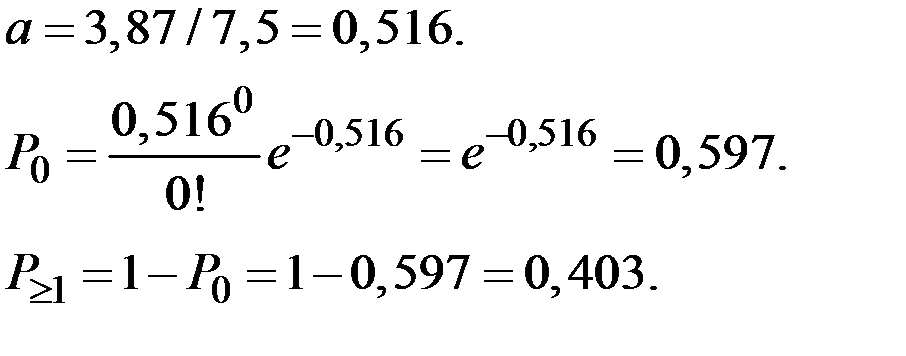
Пример 2.31. Банк выдал кредит размером 300 тыс. рублей сроком на один год под 20% годовых. Известно, что с вероятностью 0,9 заёмщик погасит кредит полностью, с вероятностью 0,06 заёмщик погасит только 50% основного долга, с вероятностью 0,04 заёмщик не погасит ничего. Найти математическое ожидание прибыли банка от этой кредитной операции.
Решение. Имеем распределение возвращённой суммы Х:
| Х | 360 | 150 | 0 |
| Р | 0,9 | 0,06 | 0,04 |
Тогда математическое ожидание возвращённой суммы банку
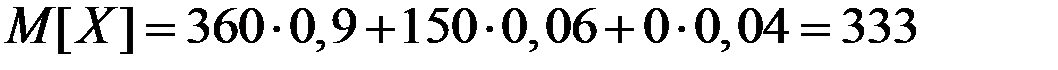тыс. руб.
Математическое ожидание прибыли банка от этой кредитной операции составит величину
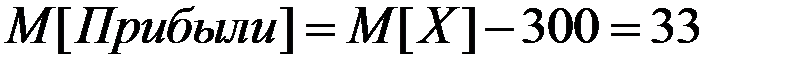тыс. руб.
Пример 2.32. Банк выдал кредит размером 300 тыс. рублей сроком на один год под 20% годовых. Известно, что с вероятностью 0,9 заёмщик погасит кредит полностью, с вероятностью 0, 06 погасит только 70% основного долга и с вероятностью 0,04 не погасит ничего. Банк застраховал свой кредитный риск в страховой компании на сумму 300 тыс. руб., купив полис, стоимостью 11 тыс. рублей. Найти математическое ожидание прибыли банка от этой кредитной операции. Определить закон распределения прибыли банка с учётом страховки.
Решение. Математическое ожидание прибыли банка от этой кредитной операции:
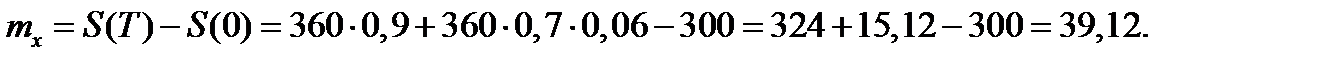
Доходность этого кредита:
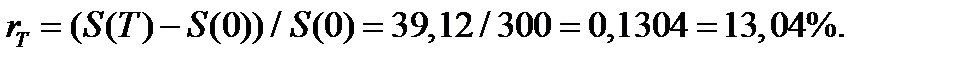
Закон распределения вероятностей прибыли банка со страховкой будет иметь вид:
| Прибыль банка, тыс. руб. | – 11 | 28,12 |
| Вероятность | 0,1 | 0,9 |
Пример 2.33. Доходы трёх банков от кредитов в отчётном году характеризуются следующими показателями:
| № банка | Средняя процентная ставка, r | Доход банка, тыс. руб., D |
| 1 | 22 | 900 |
| 2 | 15 | 1700 |
| 3 | 18 | 1400 |
Определить среднюю процентную ставку кредитов банков
Решение. Основой выбора формы средней является реальное содержание определяемого показателя:
Ставка, % = (доход банка / сумма кредита)×100%.
Средняя процентная ставка равна отношению доходов банков к сумме их кредитов. В данном примере отсутствуют прямые данные о кредитах. Но их суммы можно определить косвенным путём, разделив доход банка на процентную ставку.
Средняя процентная ставка трёх банков будет равна
.
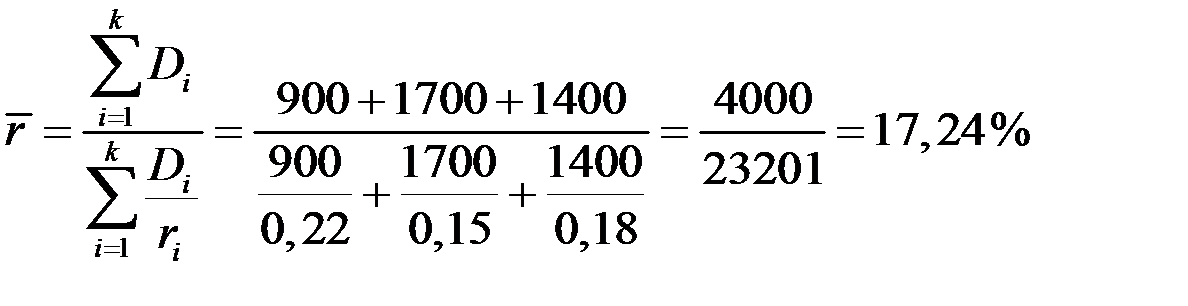В этой средней гармонической взвешенной веса представляют собой произведения процентной ставки на сумму кредита.
Пример 2.34. Имеются следующие данные о товарных запасах торгового предприятия (в млн. рублей): 1) на 01.01.2014 г.: 61,1; 2) на 01.05.2014 г.: 57,7; 3) на 01.08.2014 г.: 51,3; 4) на 01.01.2015 г.: 74,7. Определить среднемесячный товарный запас торгового предприятия за 2014 год.
Решение. По условию задачи имеем моментный ряд динамики с неравными интервалами. Поэтому среднемесячный товарный запас торгового предприятия за 2014 год рассчитаем по формуле средней хронологической с неравными интервалами:
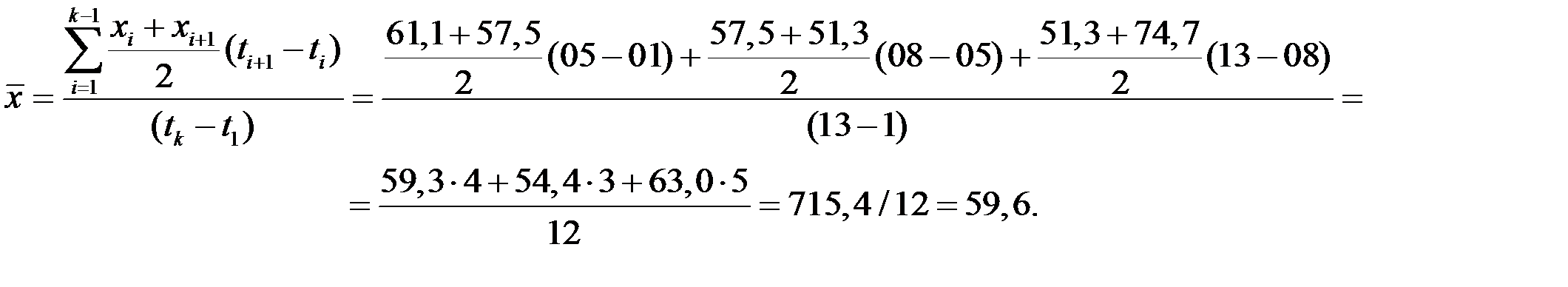
Пример 2.35. Статистический анализ данных о размерах страховых возмещений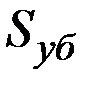 
по некоторому портфелю договоров показал, что 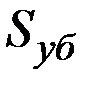имеет логарифмически нормальное распределение, т.е. величина 
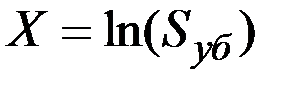имеет нормальное распределение со средним значением 
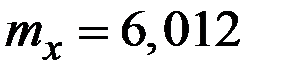долларов и средним квадратическим отклонением 
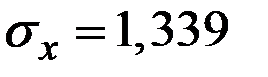долларов. Найти вероятность того, что страховое возмещение 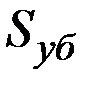индивидуального договора будет заключено в пределах от 200 до 500 долларов.
Решение.
Искомая вероятность может быть вычислена через функцию Лапласа с использованием следующего представления.
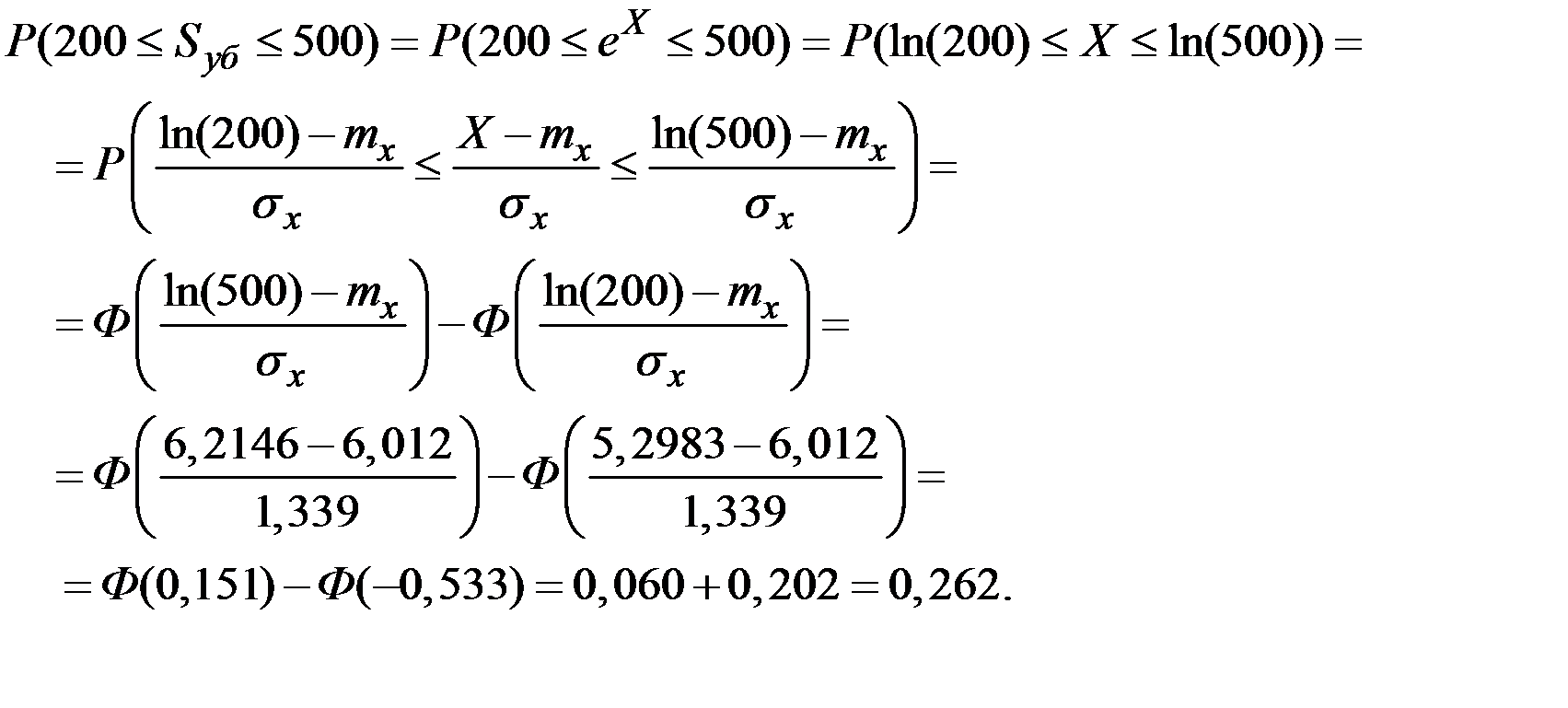
Пример 2.36. Страховая компания возмещает стоматологические расходы 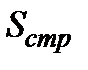вплоть до максимального значения 250 долларов. Случайная величина ущерба 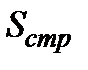распределена по показательному (экспоненциальному) закону со средним значением 250 долларов. Определить медиану распределения величины страхового возмещения.
Решение. При экспоненциальном распределении:
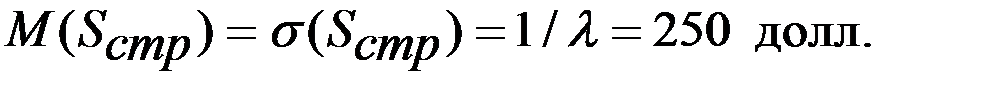
Параметр показательного закона 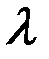= 1/120 = 0,004.
Функция распределения величины страхового возмещения имеет вид
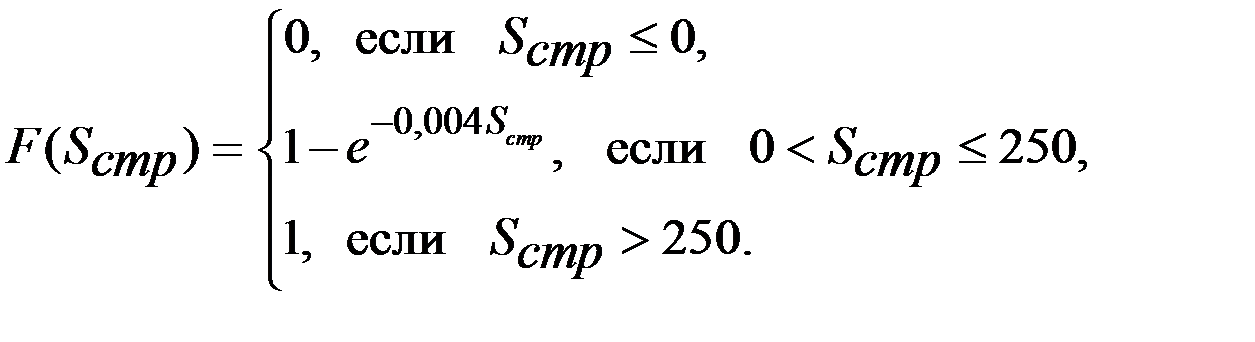
Функция распределения величины страхового возмещения возрастает от нуля до значения (при 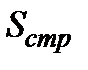= 250) 
.
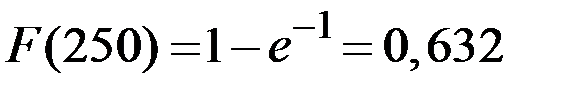Следовательно, медиана однозначно определяется из уравнения
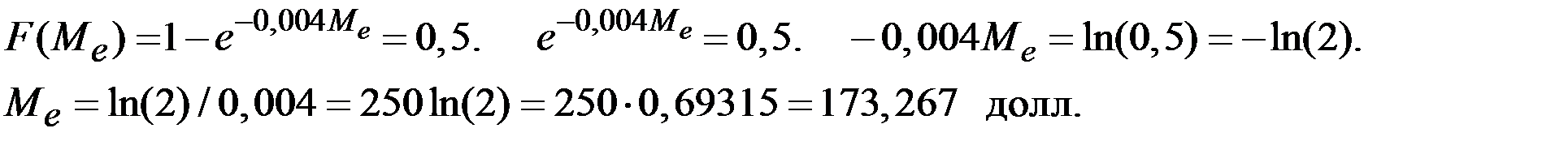
Пример 2.37. Билет на право участия в игре стоит X долларов. Игрок выбрасывает 2 игральные кости и получает выигрыш 100 долларов, если выпали две шестёрки, 10 долларов – при выпадении только одной шестёрки и проигрывает, если ни одной шестёрки не появилось. Какова должна быть минимальная стоимость билетов (целое число), чтобы игра приносила доход её устроителям?
Решение. Случайная величина X принимает значения 0; 10; 100 соответственно с вероятностями
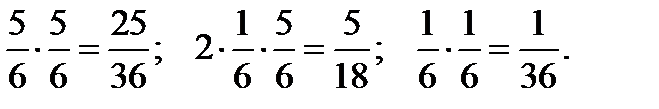
| x | 0 | 10 | 100 |
| p |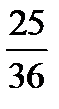 
| 
| 
|
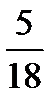
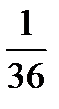
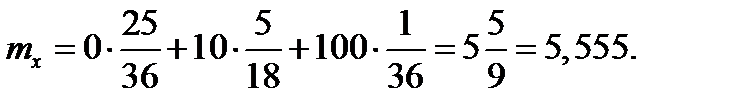
Билет должен стоить не менее 6 долларов.
Пример 2.38. Время от момента приобретения оборудования до момента его отказа имеет экспоненциальное распределение со средним значением 10 лет. Владелец оборудования решил застраховать его на случай раннего отказа. По условиям договора страховая компания выплачивает определённую страховую сумму 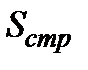в случае отказа в течение первого года эксплуатации, 50% от этой суммы в случае отказа в течение второго и третьего первого года эксплуатации и не платит ничего, если оборудование проработает без отказа три года. Известно, что ожидаемые выплаты по этому договору составляют 1000 долларов. Найти размер страховой суммы .
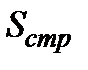Решение. При экспоненциальном распределении времени до отказа:
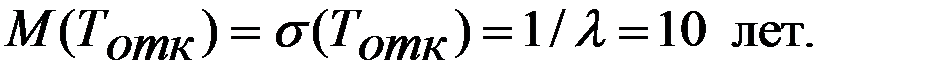
Параметр показательного закона 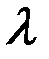= 1/10 = 0,1.
Выплаты страховщика по договору можно выразить так:
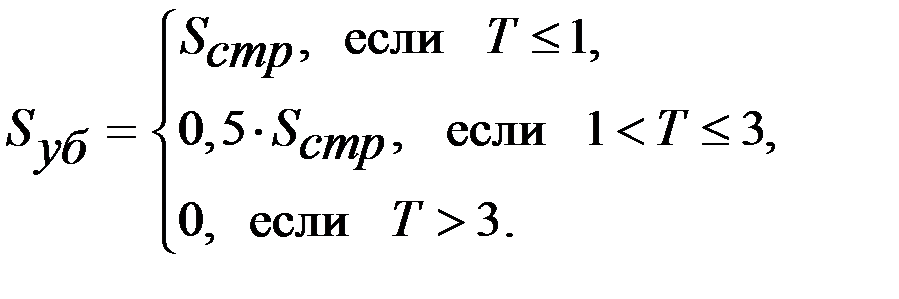
Поэтому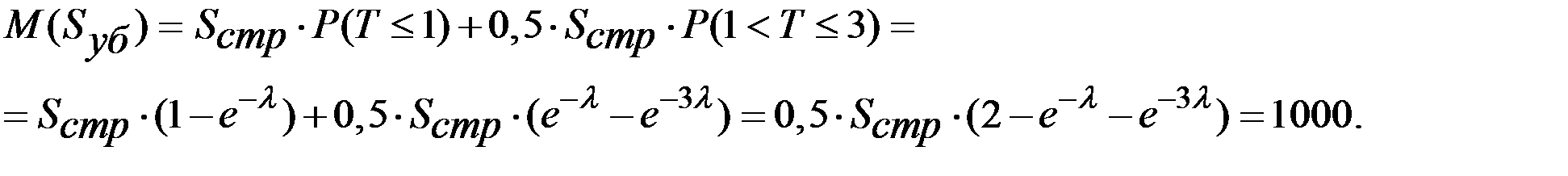
Отсюда для страховой суммы 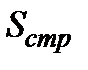имеем:
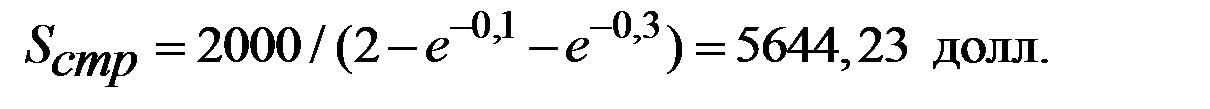
Пример 2.39. Величина ущерба по договорам автомобильного страхования имеет экспоненциальное распределение, а вероятность того, что ущерб меньше 1000 долларов, равна 0,25. Прошло 10 лет. Частота аварий и их характер не изменились, но из–за инфляции ущерб после аварии вырос в два раза по сравнению с ущербом после аналогичной аварии 10 лет назад. Найти вероятность того, что в настоящее время ущерб меньше 1000 долларов.
Решение. Пусть 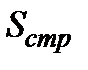– размер ущерба после аварии 10 лет назад, а 
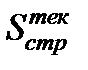– размер ущерба после аварии в настоящее время. Инфляция проявляется в том, что величина 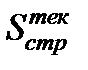/2 распределена так же как и .
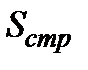Поэтому для искомой вероятности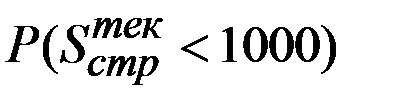 
имеем:
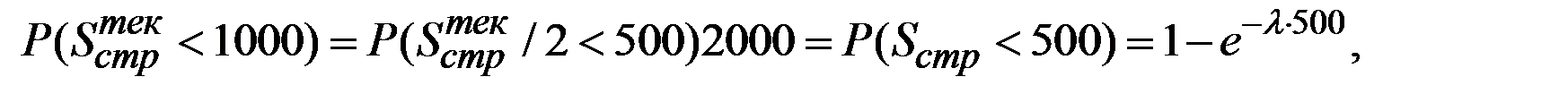
где 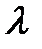– параметр экспоненциальной величины .
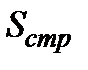По условию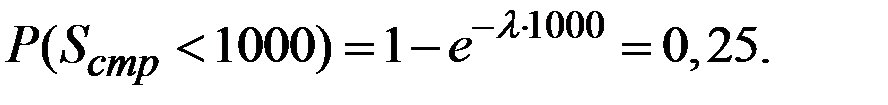 
Формулу для 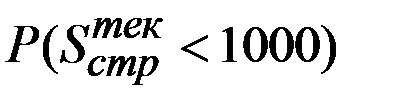можно преобразовать так:
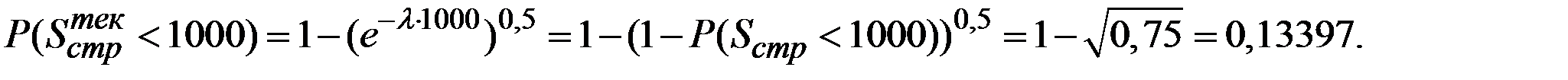
Пример 2.40. 10% договоров из портфеля страховой компании являются договорами с высокой степенью риска, оставшиеся 90% договоров являются договорами с низкой степенью риска. Число страховых случаев по одному договору в течение года распределено по закону Пуассона со средним значением а. Риски, связанные с различными договорами, независимы друг от друга. Для договоров с высокой степенью риска а = 0,6, а для договоров с низкой степенью риска а = 0,1. Сколько в среднем можно ожидать случаев в наступающем году по договору, который в прошлом году привёл к одному страховому случаю?
Решение. Введём обозначения:
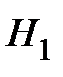– гипотеза: договор имеет высокую степенью риска;
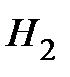– гипотеза: договор имеет низкую степенью риска;
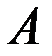– событие: договор привёл к одному страховому случаю.
По условию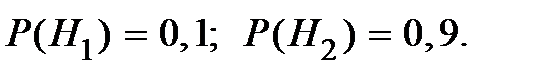
По формуле Байеса подсчитаем апостериорную вероятность того, что договор имеет высокую степенью риска
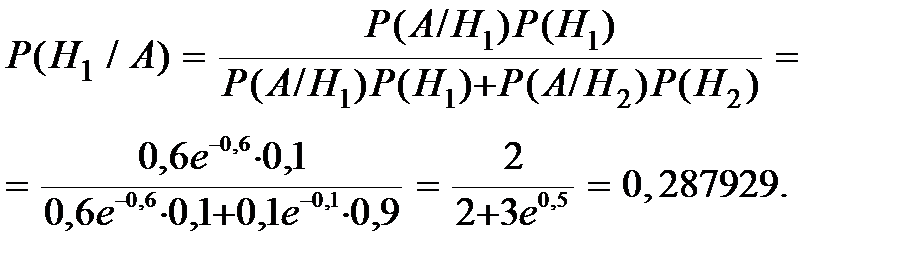
При условии, что договор имеет высокую степенью риска ожидаемое число страховых случаев в наступающем году равно 0,6.
Апостериорную вероятность договора с низкой степенью риска
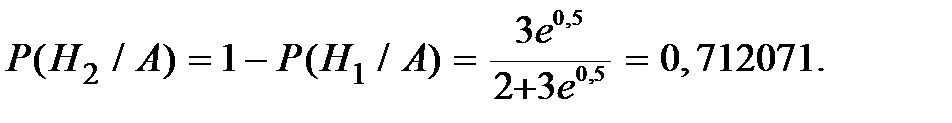
При условии, что договор имеет низкую степенью риска ожидаемое число страховых случаев в наступающем году равно 0,1.
Отсюда в среднем можно ожидать случаев в наступающем году по договору, который в прошлом году привёл к одному страховому случаю
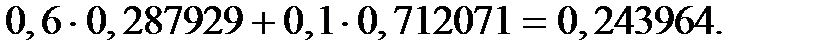
Пример 2.41. Число страховых случаев по одному договору в течение года распределено по закону Пуассона. Для половины договоров среднее число страховых случаев в год равно 2., а для другой половины – 4. По случайно взятому договору два года подряд было заявлено по 4 страховых случая в год. Сколько в среднем можно ожидать страховых случаев по этому договору в следующем году?
Решение. Введём обозначения:
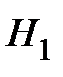– гипотеза: договор имеет в среднем 2 страховых случая в год;
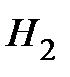– гипотеза: договор имеет в среднем 4 страховых случая в год;
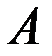– событие: договор привёл два года подряд к 4 страховым случаям в год.
По условию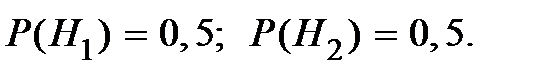
Считаем, что риски в различные годы независимы и распределены по закону Пуассона, то
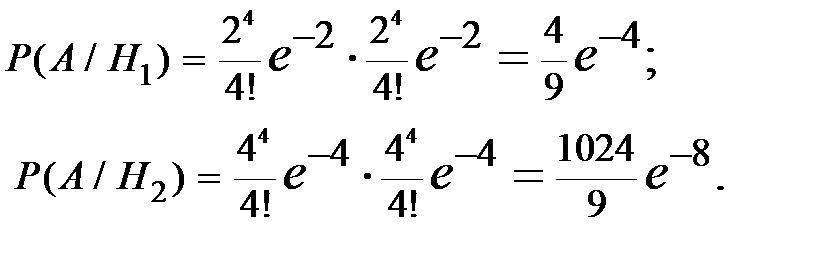
По формуле Байеса подсчитаем апостериорную вероятность того, что договор входит в первую группу
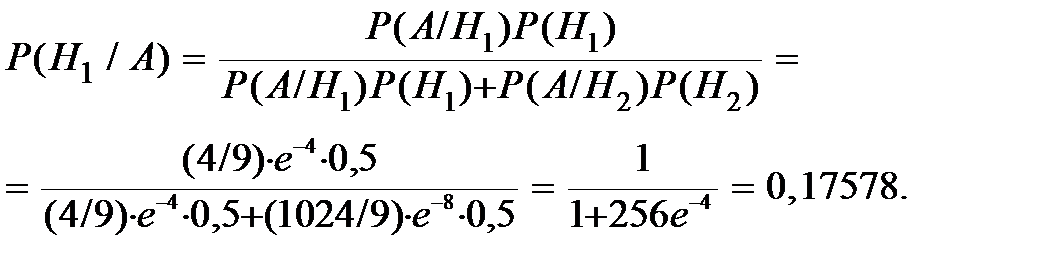
Апостериорную вероятность того, что договор входит во вторую группу
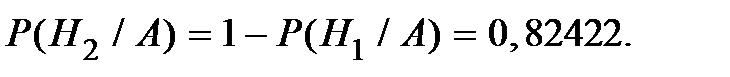
Отсюда в среднем можно ожидать случаев в наступающем году по договору, который привёл два года подряд к 4 страховым случаям в год, равно: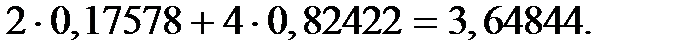
Пример 2.42. Величина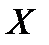 
может принимать значения: –1; 0; +1. Математическое ожидание величины равно 0,1; а её квадрата 0,9. Построить закон распределения этой величины.
Решение.
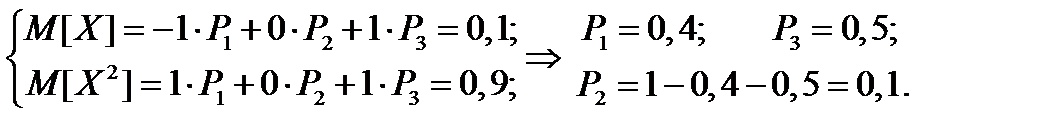
Пример 2.43. Первый студент выучил 20 билетов из 50, второй – 30, третий – 40. Студент получает зачёт, если отвечает на вопрос. Найти коэффициент вариации числа студентов (из трёх), сдавших зачёт.
Решение. Для нахождения вероятностей получения зачёта ни одним, одним, двумя тремя (их трёх) студентами воспользуемся производящей функцией
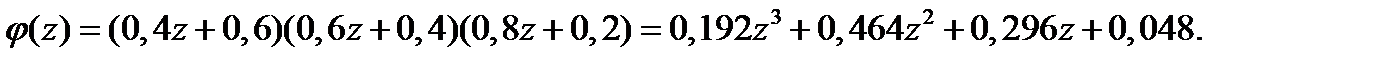
Тогда среднее число студентов, получивших зачёт, равно
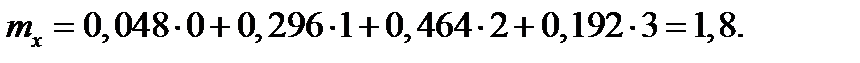
Дисперсия числа студентов, получивших зачёт, равно
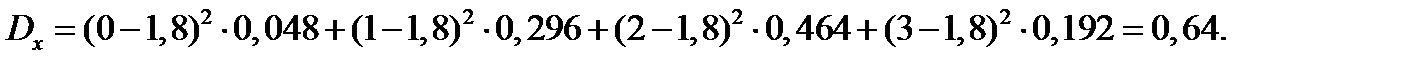
Среднее квадрат. отклонение числа студентов, получивших зачёт:
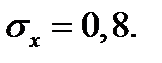
Коэффициент вариации числа студентов, сдавших зачёт, равен
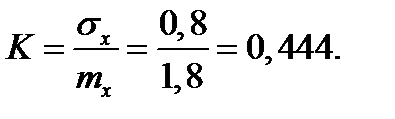
Пример 2.44. Группа студентов из 15 человек проводит собрание в зале, в котором 20 рядов по 10 мест в каждом. Каждый студент занимает место случайно. Найти вероятность того, что не более трёх студентов будет сидеть на местах с номером 7.
Решение. Вероятность занятия места №7 одним студентом равна
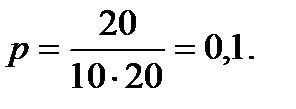
Тогда в среднем количество студентов на местах №7 окажется равным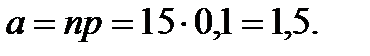 
По закону Пуассона
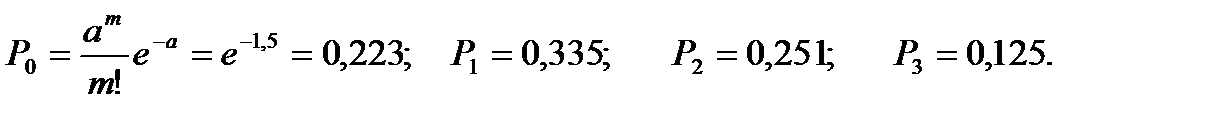
Тогда
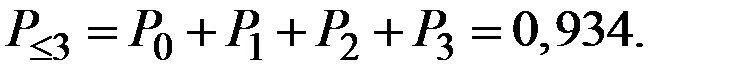
Можно по Бернулли:
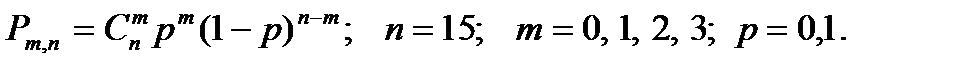
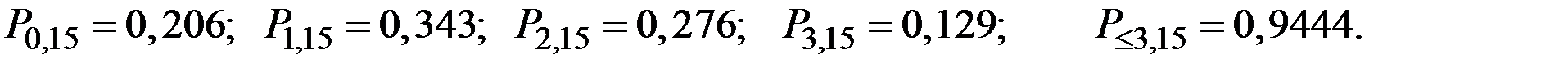
Можно через сочетания
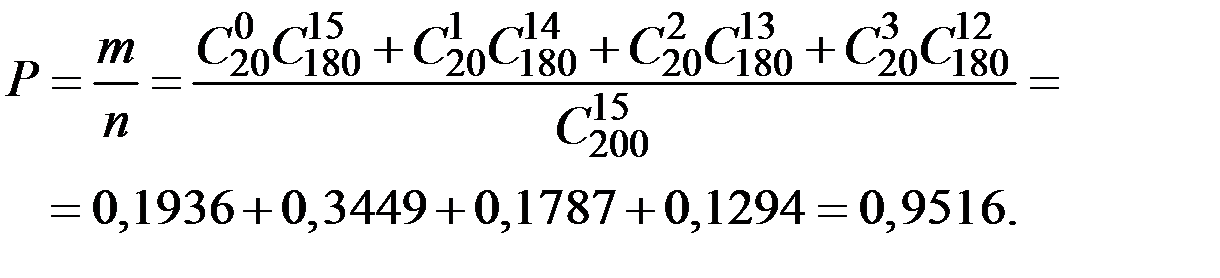
Пример 2.45. В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Составить закон распределения числа стандартных деталей среди отобранных.
Решение. СВ Х (число стандартных деталей среди отобранных) может принимать значения: 1, 2, 3 и имеет гипергеометрическое распределение. Вероятности того, что Х примет эти значения, найдём по формуле:
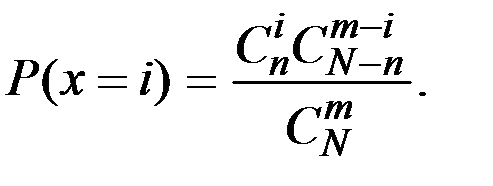
Имеем: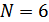 
– число деталей в партии; 
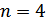– число стандартных деталей в партии; 
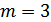– число отобранных деталей; 
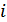– число стандартных деталей среди отобранных.
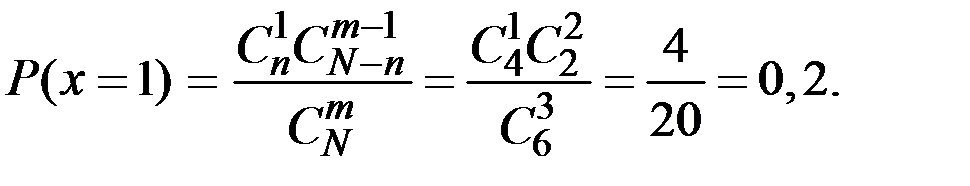
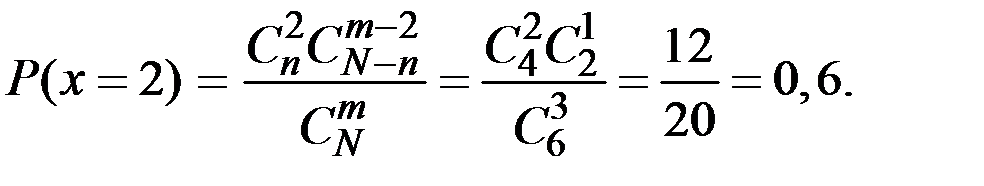
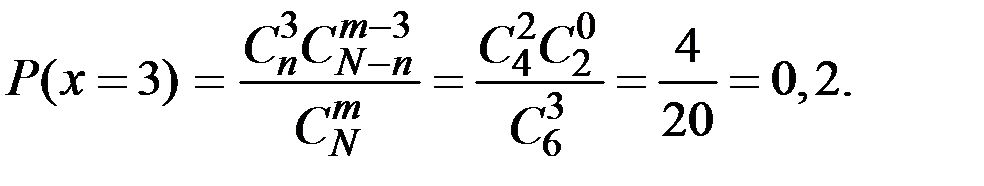
Таким образом, получаем следующий закон распределения вероятностей случайной величины Х:
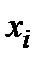
| 0 | 1 | 2 |
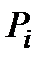
| 0,2 | 0,6 | 0,2 |
Пример 2.46. Два станка–автомата одинаковой производительности производит детали на общий конвейер. Первый станок производит 2% брака, второй – 5%. Какова вероятность того, что в ящике из 100 деталей будет не менее двух бракованных?
Решение. Применим закон Пуассона:
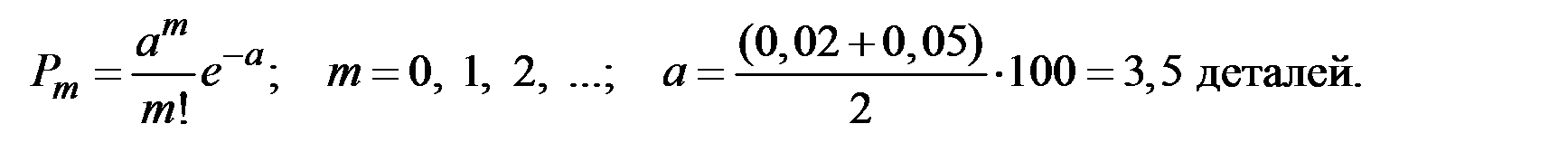
Вероятности отсутствия брака и одной бракованной детали в ящике:
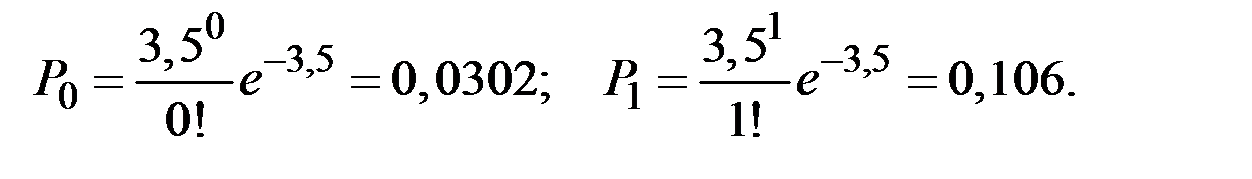
Тогда вероятность того, что в ящике из 100 деталей будет не менее двух бракованных:
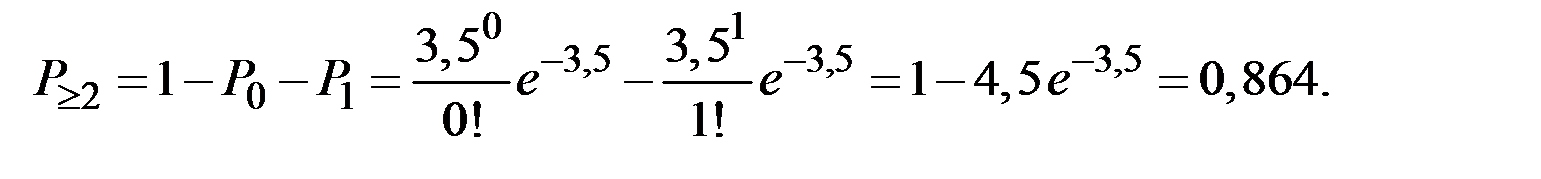
Пример 2.47. Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.
Решение: Случайная величина Х (число элементов, отказавших в одном опыте) может принимать значения: 0, 1, 2, 3. Вероятности того, что Х примет эти значения, найдём по формуле Бернулли:
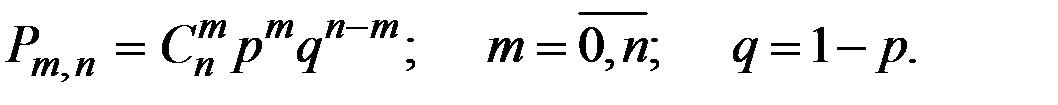
Получаем:
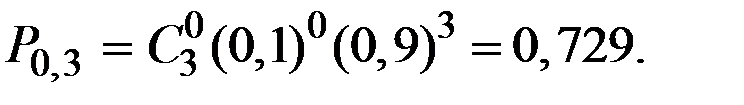
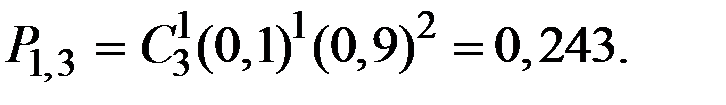
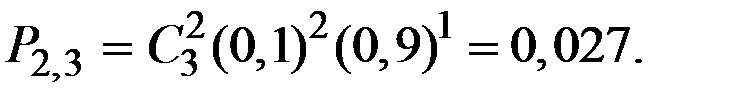
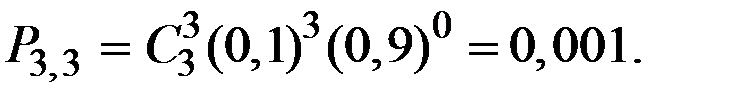
Таким образом, получаем следующий закон распределения вероятностей случайной величины Х:
|
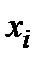
| 0 | 1 | 2 | 3 |
|
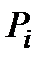
| 0,729 | 0,243 | 0,027 | 0,001 |
Пример 2.48. Задан закон распределения случайной величины Х:
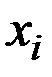
| 29 | 31 | 34 | 49 |
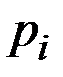
| 0,091 | 0,181 | 0,271 | 0,456 |
Найти коэффициент вариации данной случайной величины.
Решение. Для нахождения коэффициента вариации величины надо найти математическое ожидание и среднее квадратическое отклонение данной случайной величины.
Математическое ожидание вычисляем по формуле:
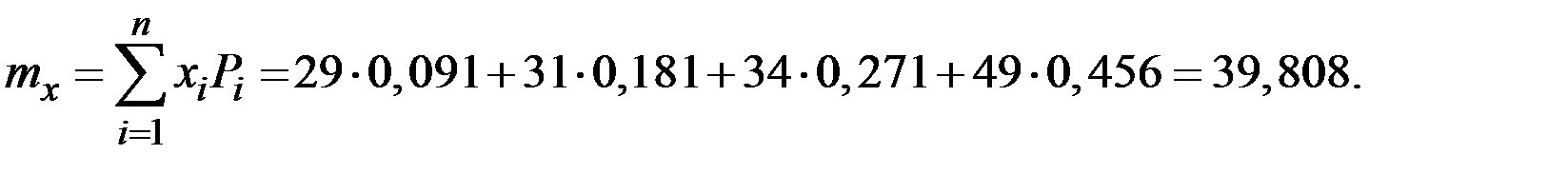
Дисперсию находим по формуле:
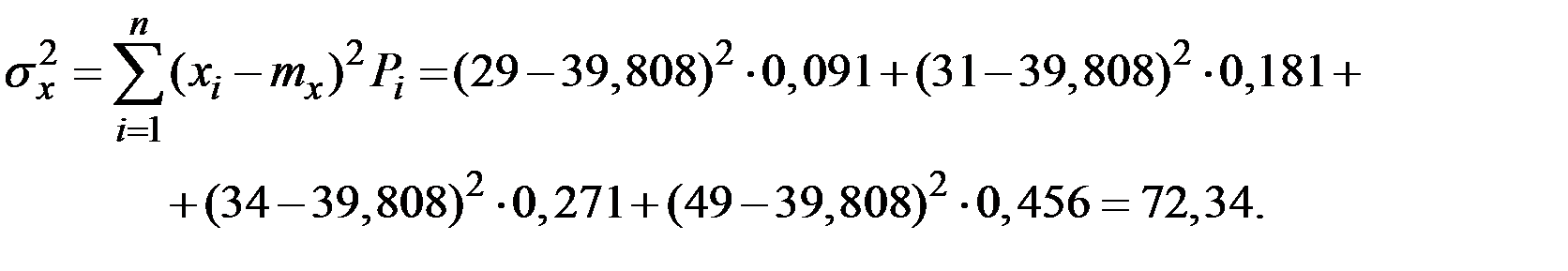
Среднее квадратическое отклонение – это квадратный корень из дисперсии:
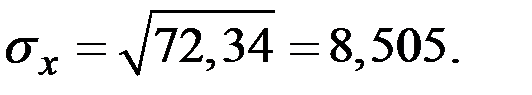
Коэффициент вариации случайной величины равен отношению среднего квадратического отклонения к математическому ожиданию (характеризует относительную изменчивость величины):
