Функция распределения выражается площадью функции плотности распределения, лежащей левее точки х. Следовательно

Дата: 2025-06-02; Просмотры: 16

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

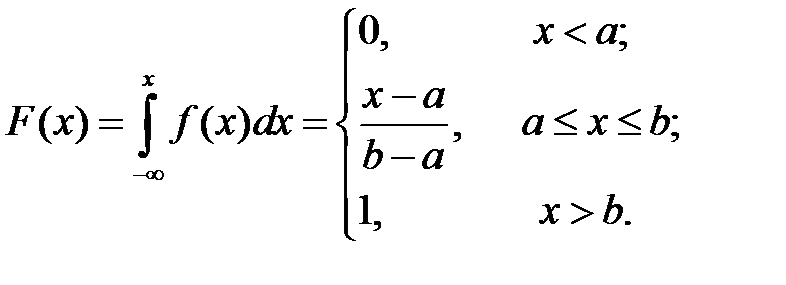
Определим основные числовые характеристики этого закона.

Математическое ожидание

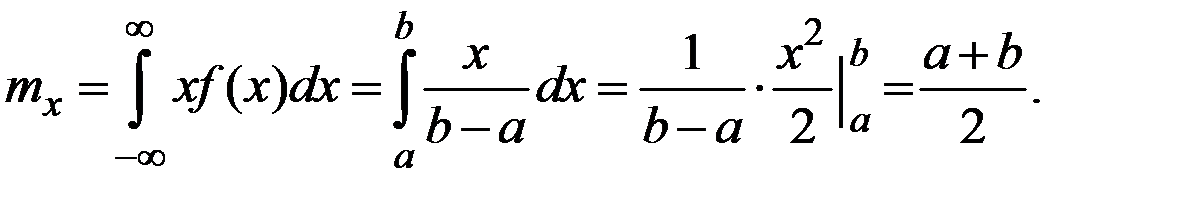
В силу симметричности равномерного распределения медиана величины Х также равна .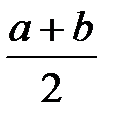

Моды закон равномерной плотности не имеет.

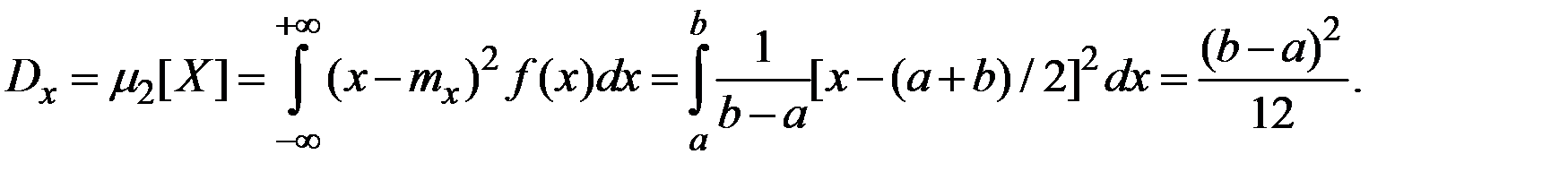
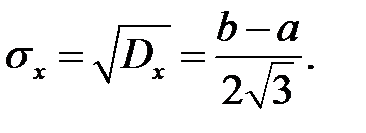
В силу симметричности распределения его асимметрия равна нулю.

.

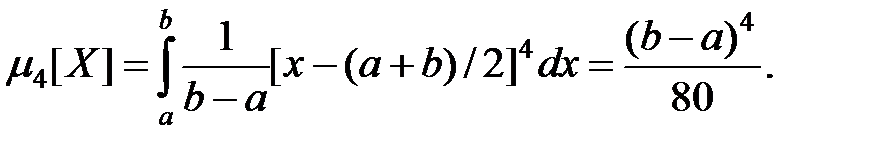
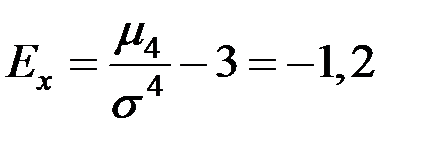2.3.2. Закон Пуассона

Дискретная СВ Х распределена по закону Пуассона, если вероятность того, что она примет определённое значение m, выражается формулой:

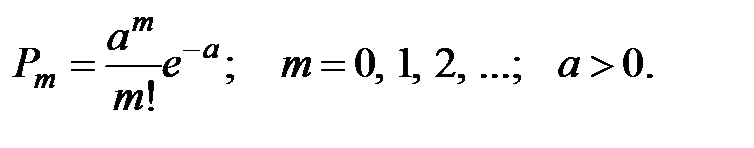
Для закона Пуассона справедливо соотношение

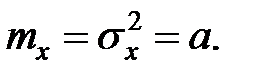
Типичная задача, приводящая к распределению Пуассона, заключается в следующем.

Пусть на оси 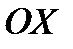случайным образом распределяются точки.

Допустим, что случайное распределение точек удовлетворяет следующим условиям.

1. Вероятность попадания того или иного числа точек на отрезок 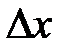зависит только от длины этого отрезка, но не зависит от его положения на оси, т.е. точки распределены на оси с одинаковой средней плотностью (интенсивностью) 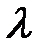(математическое ожидание числа точек, приходящихся на единицу длины, равно ).

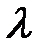2. Точки распределяются на оси независимо друг от друга, т.е. вероятность попадания того или иного числа точек на заданный отрезок не зависит от того, сколько их попало на любой другой отрезок, не перекрывающийся с ним (нет последействия).

3. Вероятность попадания на малый участок х двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки (это условие означает практическую невозможность совпадения двух или более точек, точки следуют по одной).

Исходя из этих условий можно доказать, что число точек, попадающих на заданный отрезок длины х на оси 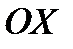, подчиняется закону распределения Пуассона

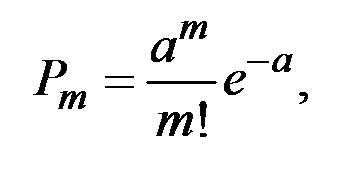
где а = х.

Величина а по смыслу представляет собой среднее число точек, приходящееся на отрезок х.

Распределение Пуассона возникает там, где какие–то точки (или другие элементы) занимают случайное положение независимо друг от друга, и подсчитывается количество этих точек, попавших в заданную область.

Закон Пуассона часто называют законом редких явлений из–за свойства выражать биномиальное распределение при большом числе опытов и малой вероятности события:

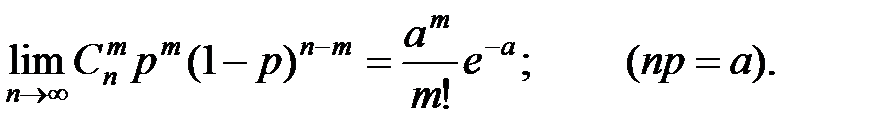
На практике часто при решении вопроса о принятии закона Пуассона для описания какой–то СВ определяют из опыта её математическое ожидание и дисперсию. Если их значения близки, то это может служить в пользу гипотезы о пуассоновском распределении. Резкое различие этих характеристик, напротив, свидетельствует против этой гипотезы.

Пример 2.8. Брокеру поступают заявки на операции с ценными бумагами со средней плотностью 15 заявок в час. Определить вероятность того, что за две минуты брокеру поступит: ровно три заявки; хотя бы одна заявка.

Решение. Считаем, что число заявок на любом участке времени распределено по закону Пуассона.

Среднее число заявок за две минуты

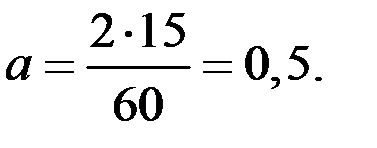
Тогда вероятность поступления ровно трёх заявок равна:

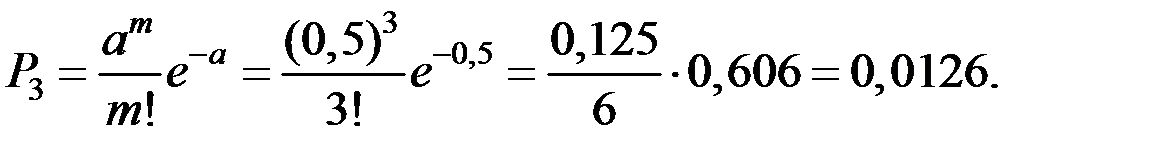
Вероятность того, что поступит хотя бы одна заявка за две минуты

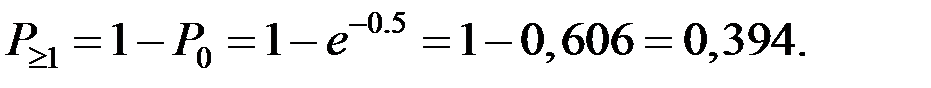
2.3.3. Показательное распределение

Показательным (экспоненциальным) называют распределение вероятностей СВ Х, которое описывается дифференциальной функцией

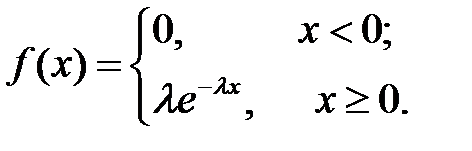
Следовательно,

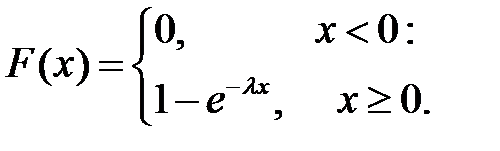
Тогда вероятность попадания СВ Х в интервал (а, b) определится следующим образом:

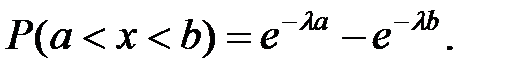
Можно показать, что у показательного распределения

.

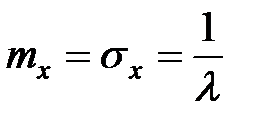Показательное распределение хорошо описывает время обслуживания клиента в системе массового обслуживания (магазины, службы быта, справочные и т.п.), длительность наработки устройства на отказ.

В частности, вероятность отказа за время t выражается функцией распределения

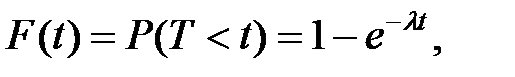
где 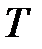– длительность времени безотказной работы,

 – интенсивность отказов.

Пример 2.9. Время ожидания связи с оператором банка подчиняется показательному закону распределения со средним значением 30 секунд. Найти вероятность того, что клиент будет ожидать связи с оператором более 40 секунд.

Решение. В этом примере математическое ожидание 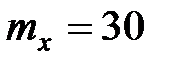сек., а интенсивность отказов равна

.

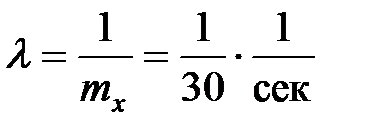Тогда искомая вероятность

.

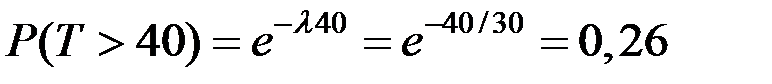2.3.4. Нормальный закон распределения

Нормальный закон распределения (закон Гаусса) характеризуется плотностью вероятностей следующего вида:

.

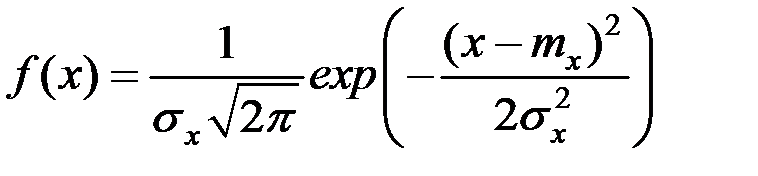На практике часто оперируют случайными величинами, распределёнными по нормальному закону.

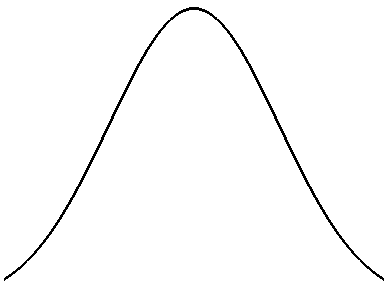
Нормальное распределение характеризуется тем, что крайние значения случайной величины в нём встречаются достаточно редко, а значения, близкие к средней величине – достаточно часто (рис. 2.3).

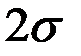
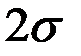
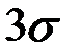
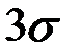
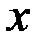
Рис. 2.3. Нормальный закон распределения

Нормальный закон – это двухпараметрический закон.

Параметр 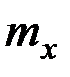определяет положение центра рассеяния случайной величины, а параметр 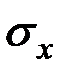характеризует меру её рассеяния относительно центра.

Функция распределения нормального закона не выражается в явном виде через элементарные функции и для её вычисления используют табличные (стандартные) функции типа интеграла вероятностей.

Часто функция распределения нормального закона определяется соотношением:

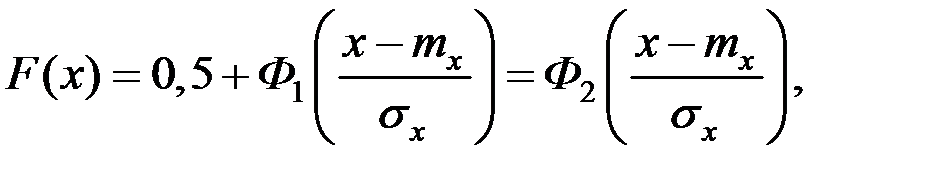
где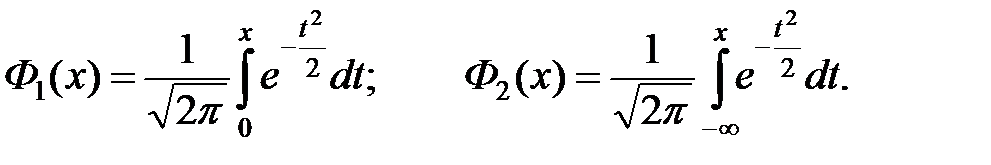

Здесь 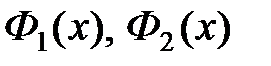– стандартные функции Лапласа (интегралы вероятностей). Эти функции табулированы и широко используются в практических расчётах.

Возьмём за основу функцию 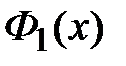, будем обозначать её 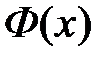(без индекса), и именно её будем иметь в виду, говоря о функции Лапласа.

Функция Лапласа 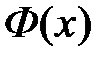имеет следующие свойства:

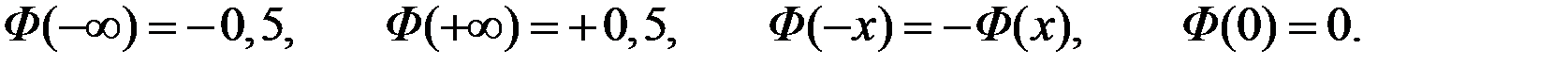
Для центральных моментов существует рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков: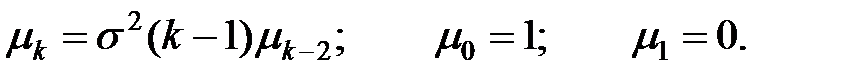

Нормальный закон распределения широко используется на практике и возникает там, где случайная величина образуется в результате совокупного влияния многих других случайных факторов.

Вероятность попадания нормальной случайной величины Х на участок от 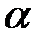до 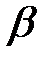выражается через функцию Лапласа:

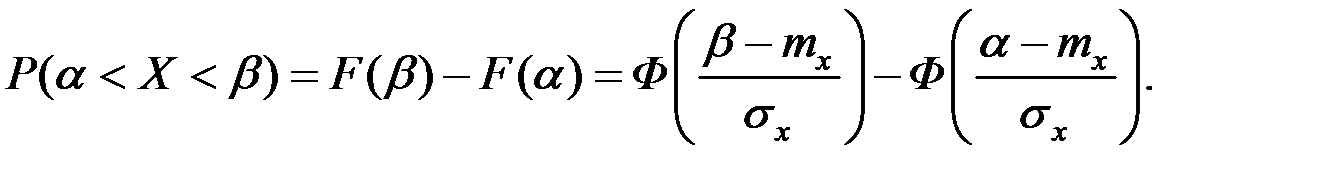
Найдём вероятность попадания нормальной СВ в отрезки, равные 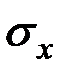, прилегающие последовательно к точке математического ожидания.

Получим:

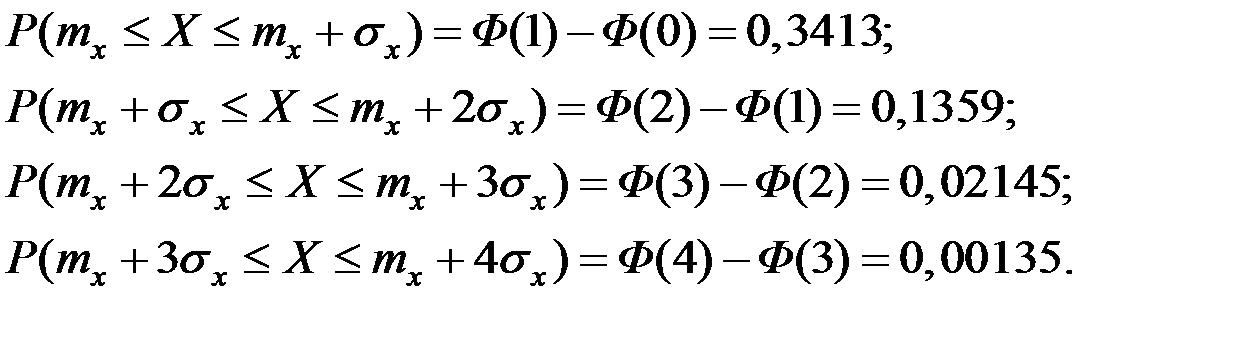
Правило трёх сигм для нормального закона можно выразить соотношением:

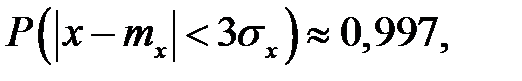
т.е. с точностью до тысячных весь диапазон разброса значений СВ с нормальным законом распределения заключён в пределах ± 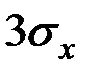от центра величины.

Если исследователю известно, что изучаемый экономический показатель подчиняется нормальному закону распределения, то знание математического ожидания и среднего квадратического отклонения (дисперсии) даёт ему основание осуществить прогноз развития экономической ситуации.

Если случайная величина подчиняется нормальному закону, то с вероятностью 0,683 результат любого единичного её измерения лежит в интервале 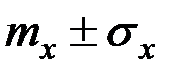; с вероятностью 0,954 он попадает в интервал 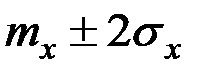; с вероятностью 0,997 – в интервал .

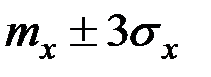Например, пусть известно, что среднее значение доходности акций фирмы равно 15% при среднеквадратичном отклонении .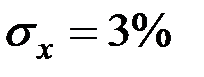

Тогда, если доходность акций подчиняется нормальному закону распределения, прогнозируемая доходность по акциям фирмы будет лежать в диапазоне 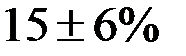с вероятностью 0,954 и в диапазоне 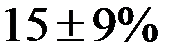вероятностью 0,997.

Пример 2.10. Деталь, изготовленная станком–автоматом, считается годной, если отклонение её контролируемого размера от проектного не превышает 1 мм. Случайные отклонения контролируемого размера от проектного подчинены нормальному закону с параметрами (мм) .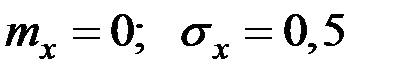

Сколько процентов годных деталей изготавливает станок?

Решение. Искомую вероятность определяем с использованием функции Лапласа:

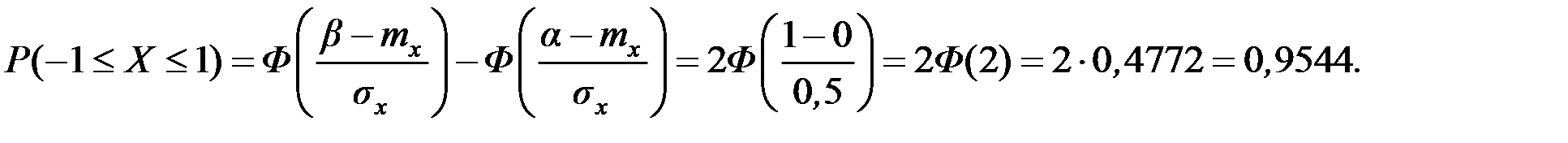
Станок изготавливает 95,44% годных деталей.

2.3.5. Логарифмическое нормальное распределение

Случайная величина X имеет логарифмически нормальное (логнормальное) распределение с параметрами (m, s ²), если

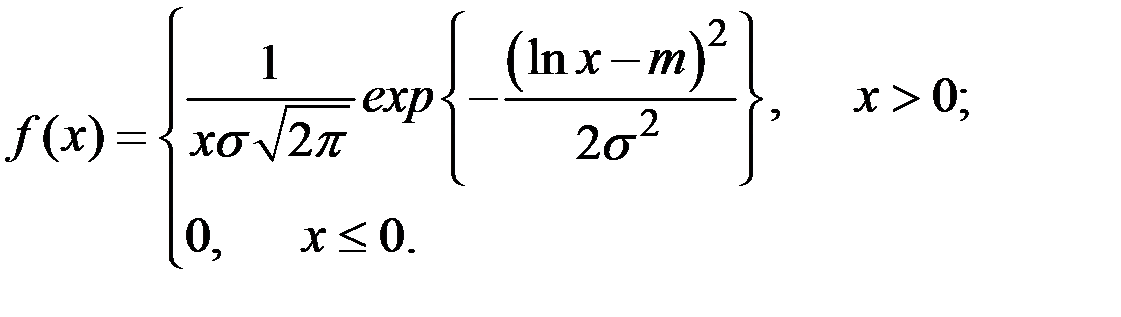
Если случайная величина Y имеет стандартное нормальное (нормированное) распределение 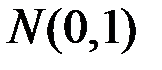, то величина

Х = exp(s Y + m)

имеет логнормальное распределение с параметрами (m, s ²).

Моменты логнормального распределения имеют выражения:

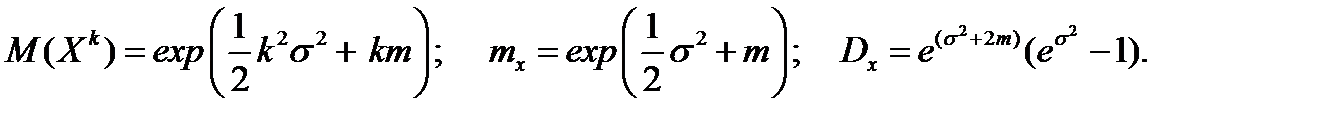
2.3.6. Распределение Бернулли

Случайная величина X имеет распределение Бернулли с параметром p (0 < p <1), если

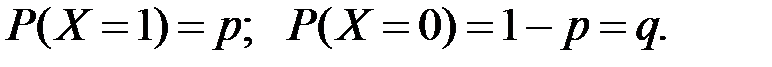
Распределение Бернулли представляет собой модель любого случайного эксперимента, исходы которого принадлежат двум взаимно исключающим классам. Функция распределения:

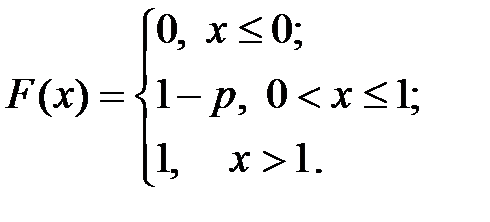
Моменты величины X :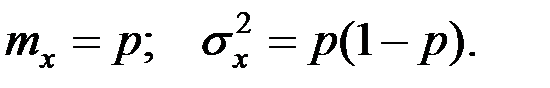

2.3.7. Биномиальное распределение

Случайная величина X имеет биномиальное распределение с параметрами n, p (0 < p < 1, n і 1) (вероятность появления ровно k событий в n опытах), если

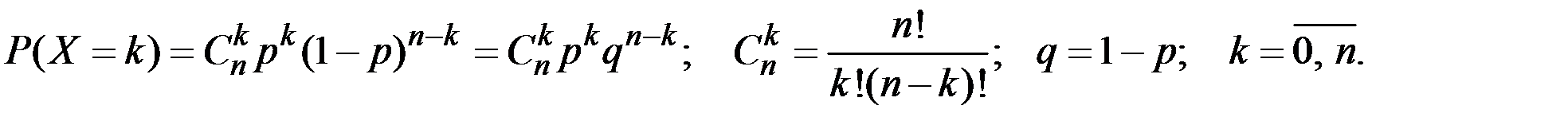
Биномиальное распределение является моделью случайных экспериментов, состоящих из n независимых однородных испытаний Бернулли.

Если Х_k (k = 1, …, n) независимы и имеют распределение Бернулли с параметром p, то случайная величина 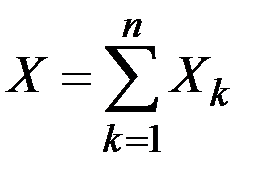имеет биномиальное распределение с параметрами (n, p).

Функция распределения:

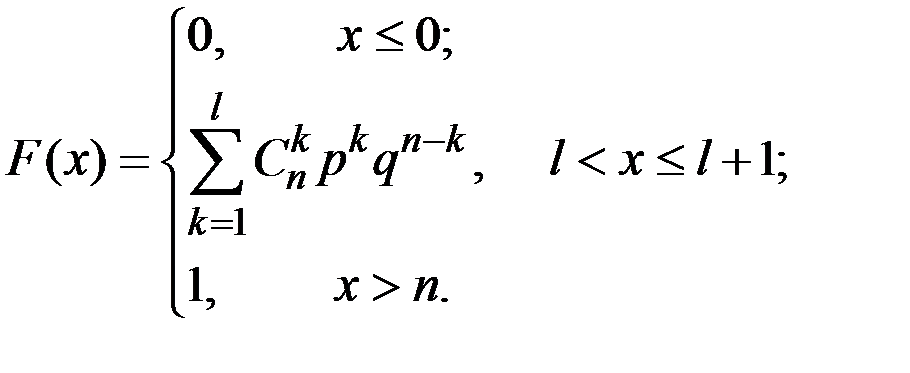
Моменты распределения:

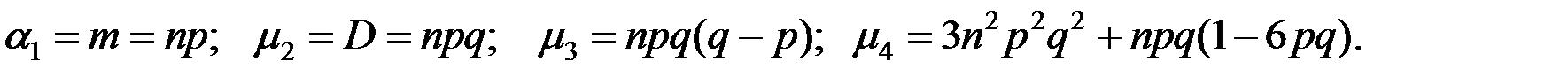
Отрицательное биномиальное распределение (число n испытаний до k –го успеха) имеет вид

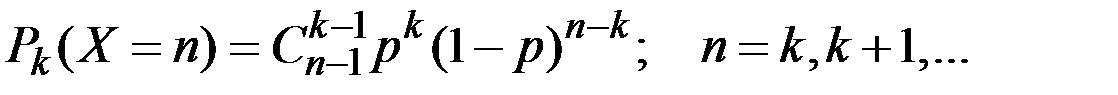
Моменты распределения:

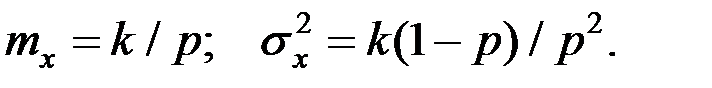
2.3.8. Геометрическое распределение

Пусть Х – число испытаний, которое нужно провести до первого появления события А, вероятность которого в одном опыте равна Р.

Тогда

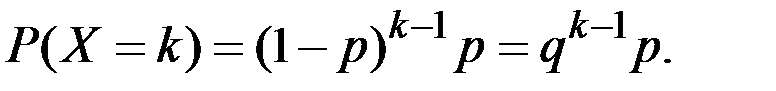
Это вероятность появления события А в k–м опыте и есть геометрическое распределение. Для различных k имеем геометрическую прогрессию с первым членом 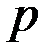и знаменателем .

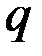Моменты: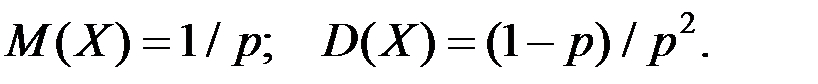

Если будем рассматривать число неудач k до первого успеха то

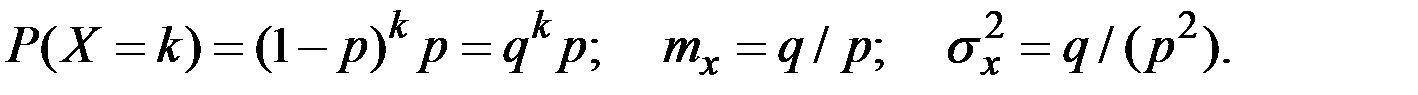
2.3.9. Гипергеометрическое распределение

Случайная величина X имеет гипергеометрическое распределение с параметрами N, p, n (0 < p < 1), если

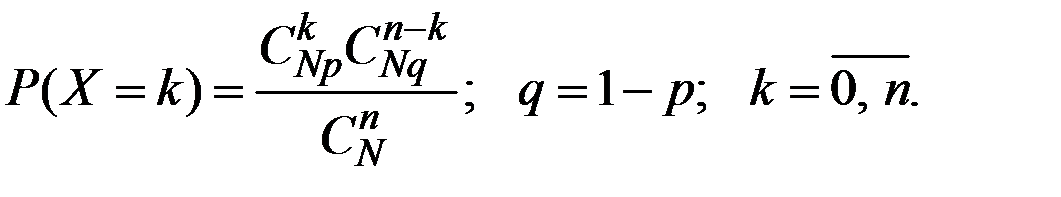
Гипергеометрическое распределение можно интерпретировать следующим образом. Из партии продукции, содержащей Np годных и Nq бракованных изделий, случайным образом выбирают n изделий. Число годных изделий описывается гипергеометрическим распределением.

Моменты:

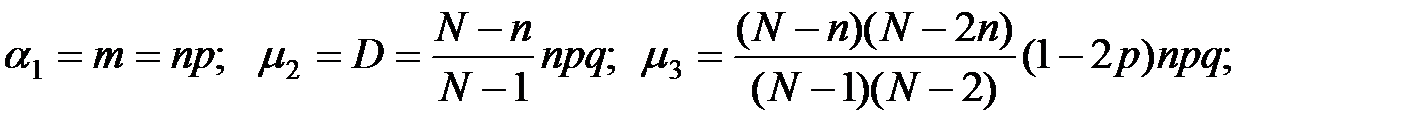
Если n << N (практически n < 0,1N), то можно использовать приближенную формулу, аппроксимирующую гипергеометрическое распределение биномиальным:

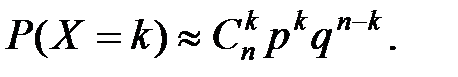
2.3.10. Распределение c ²

Случайная величина X имеет c² – распределение с n степенями свободы, если

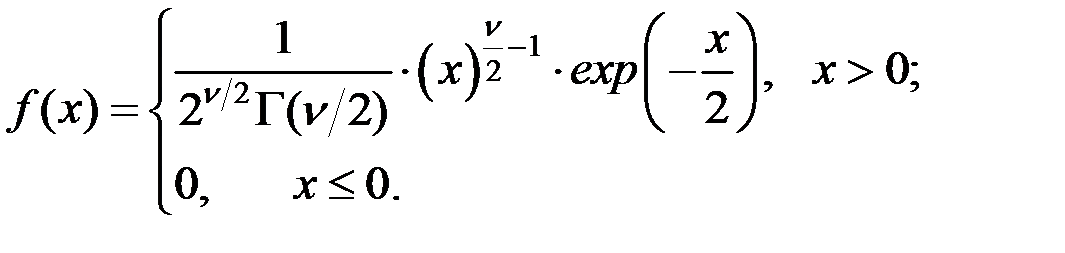
Здесь 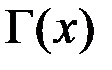– гамма функция.

Распределение c ² интерпретируется следующим образом.

Пусть X₁, X₂, …, X _n – независимые одинаково распределённые случайные величины, каждая из которых имеет нормальное распределение с нулевым средним и единичной дисперсией. Тогда величина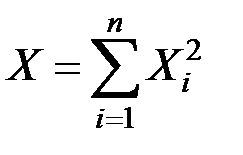

имеет распределение c ² с n степенями свободы.

Моменты: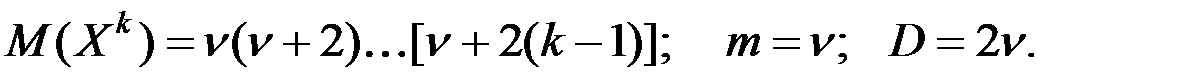

2.3.11. T–распределение Стьюдента

Величина X имеет распределение Стьюдента (T–распределение) с ν степенями свободы (ν > 0), если

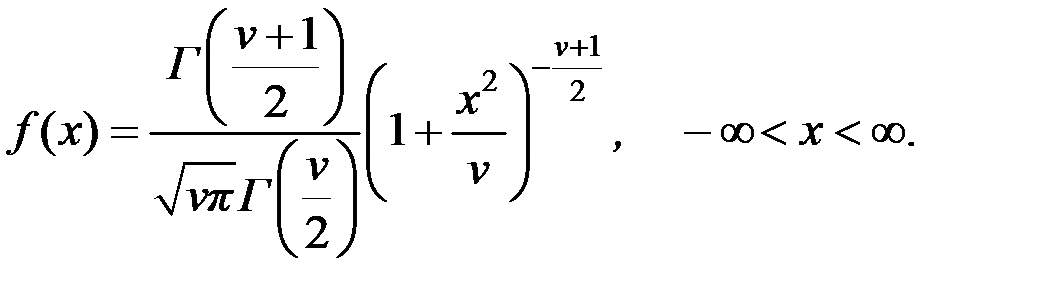
Если X₁ – случайная величина, подчиняющаяся нормальному распределению с нулевым математическим ожиданием и единичной дисперсией, X₂ – случайная величина с распределением c ² с n степенями свободы, то случайная величина

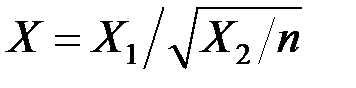
имеет T–распределение Стьюдента с n степенями свободы.

При n = 1 распределение Стьюдента совпадает с распределением Коши.

Моменты распределение Стьюдента:

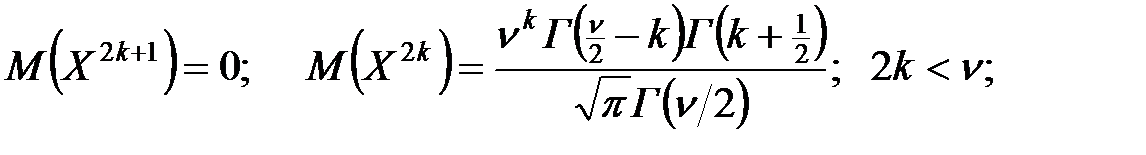
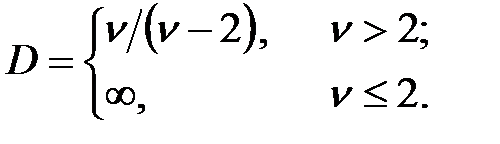
2.3.12. F–распределение

Случайная величина X имеет F–распределение (распределение Фишера–Снедекора) с (n₁, n₂) степенями свободы, если

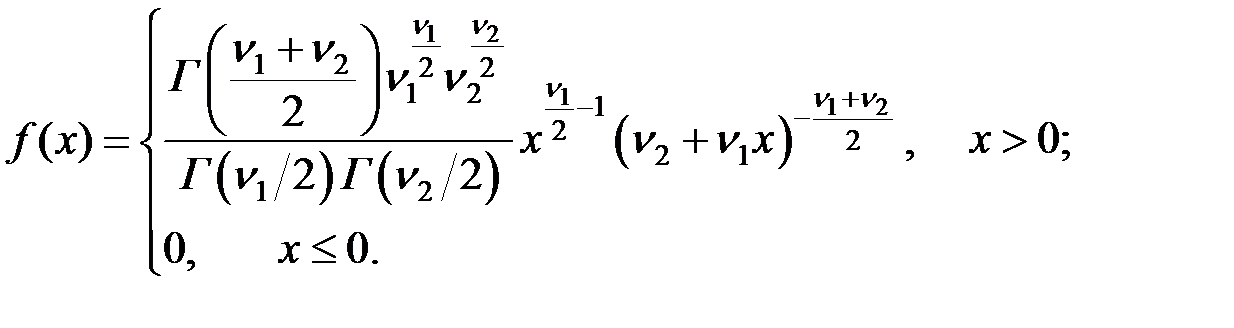
Если X₁ и X₂ – независимые случайные величины, имеющие c ² – распределение соответственно с n₁ и n₂ степенями свободы, то случайная величина 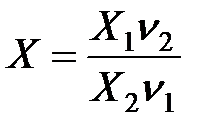имеет F–распределение с (n₁, n₂) степенями свободы.

Моменты: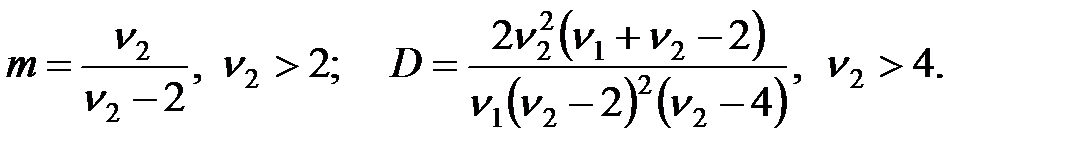

2.3.13. Треугольное распределение

Случайная величина X имеет треугольное распределение (распределение Симпсона) на отрезке [a, b], если

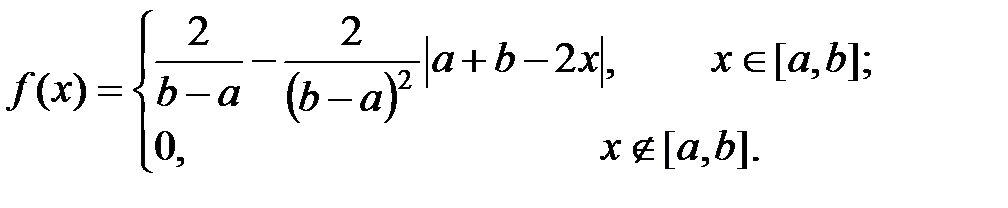
Моменты:

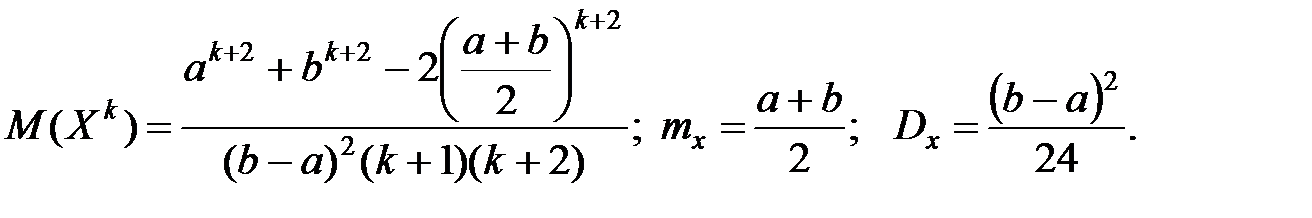
Если Х₁ и Х₂ – независимые случайные величины, равномерно распределённые на отрезке [a/2, b/2], то случайная величина Х = Х₁ + Х₂ имеет треугольное распределение.

2.3.14. Усечённые законы распределения