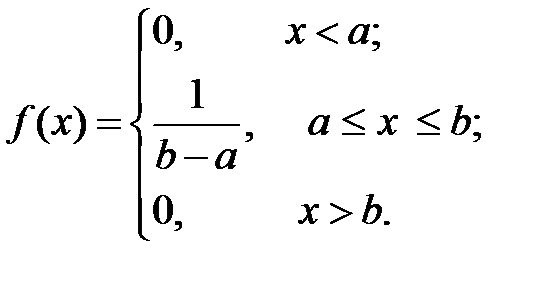Взвешенные средние используются, если первичные значения показателей ( ) сгруппированы в k вариантов (групп, интервалов, классов) и значения i–го варианта повторяются раз ( ).
Формулы средних (кроме хронологической) получаются из общей формулы степенной средней m–го порядка:
простой 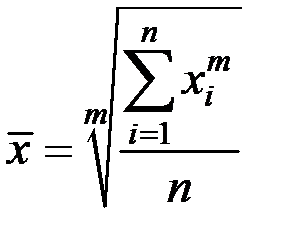 или взвешенной
или взвешенной 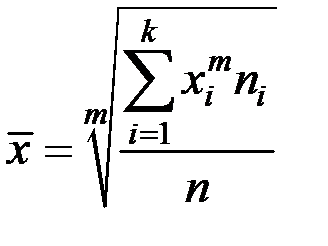 .
.
При m = –1 получаем среднюю гармоническую величину.
При m = 0 получаем среднюю геометрическую величину.
При m = 1 получаем среднюю арифметическую величину.
При m = 2 получаем среднюю квадратическую величину.
Таблица 2.1
Формулы расчёта различных видов средних величин
| № п/п | Наименование средней | Формулы средних | |
| простой | взвешенной | ||
| 1 | Средняя арифметическая | 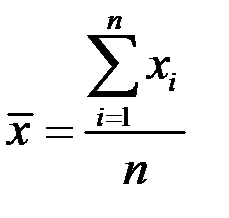
| 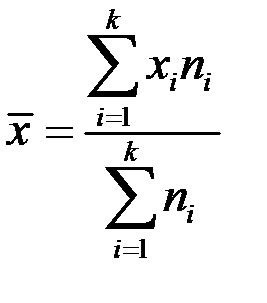
|
| 2 | Средняя геометрическая | 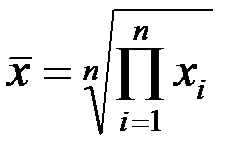
| 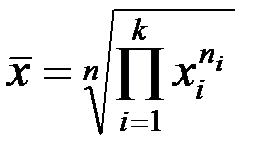
|
| 3 | Средняя гармоническая | 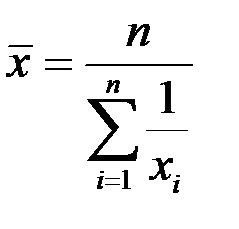
|  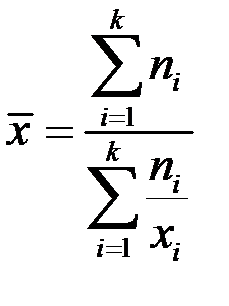
|
| 4 | Средняя квадратическая | 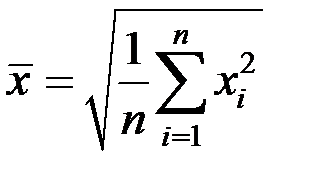
| 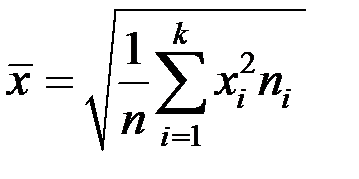
|
| 5 | Средняя хронологическая | 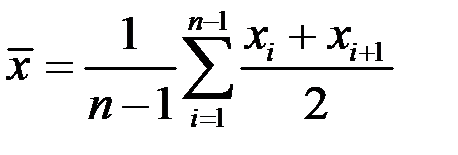
| 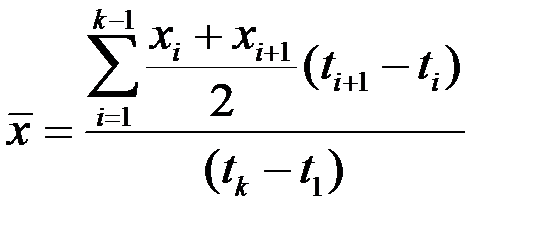
|
Мажорантность средних – свойство степенных средних возрастать с повышением показателя степени m при одних и тех же значениях 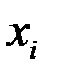 :
:
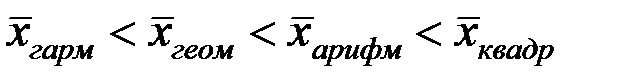 .
.
Средняя гармоническая вычисляется в тех случаях, когда средняя предназначается для расчёта сумм слагаемых, обратно пропорциональных величине заданного признака, т.е. когда суммированию подлежат не сами варианты, а обратные им величины.
Средняя хронологическая вычисляется в тех случаях, когда значения показателя ( 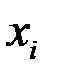 ) известны в конкретные моменты времени (
) известны в конкретные моменты времени ( 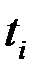 ).
).
Средняя геометрическая используется при вычислении средних темпов прироста исследуемых показателей.
Для характеристики размеров колеблемости признаков в статистике применяются следующие показатели: размах колебаний (вариации), среднее линейное отклонение, дисперсия, среднее квадратичное отклонение (табл. 2.2).
Таблица 2.2
Формулы расчёта показателей вариации
| № п/п | Наименование показателя | Формулы расчёта | |
| для несгруппированных данных | для сгруппированных данных | ||
| 1 | Размах колебаний | 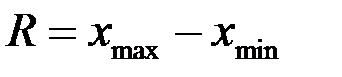
| 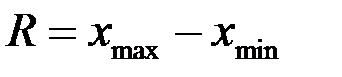
|
| 2 | Среднее линейное отклонение | 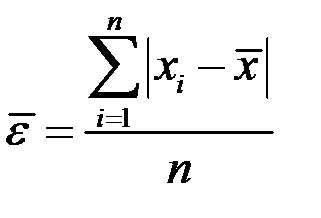
| 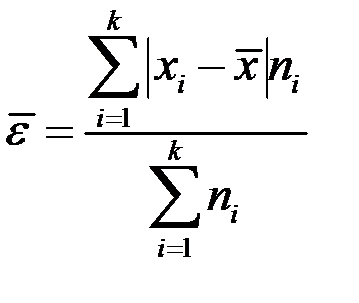
|
| 3 | Дисперсия | 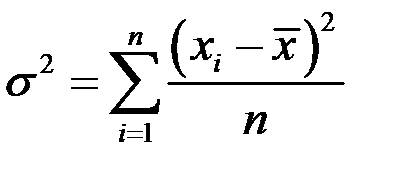
|  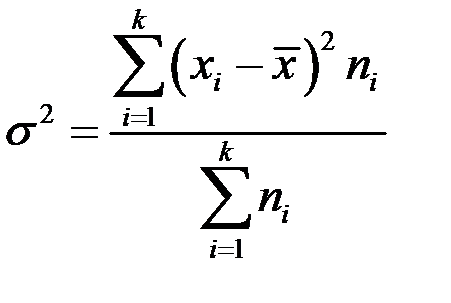
|
| 4 | Среднее квадратическое отклонение | 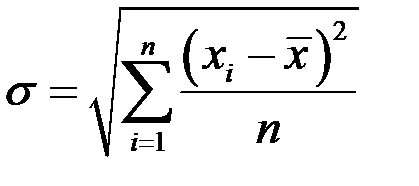
| 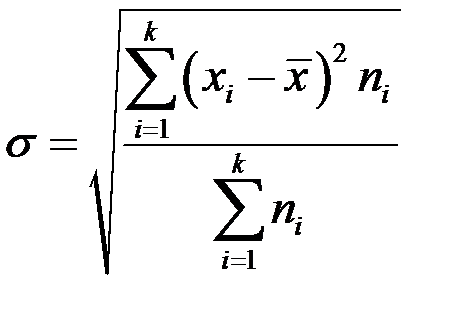
|
Дополнительно к показателям табл. 2.2 можно отметить следующие показателей вариации:
квартильные отношения:
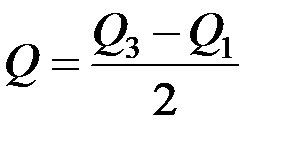 ;
;
децильные отношения:
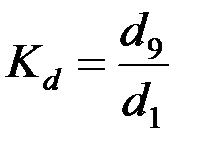 .
.
Дециль – вариант ранжированного ряда, отсекающий десятую часть совокупности.
Квартили – значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине 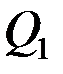 ; 25% единиц совокупности будут заключены между
; 25% единиц совокупности будут заключены между 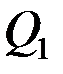 и
и 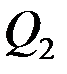 ; 25% – между
; 25% – между 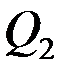 и
и 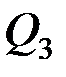 .
.
Относительные показатели вариации приведены в табл. 2.3.
Относительные показатели вариации часто измеряются в процентах.
Таблица 2.3
Относительные показатели вариации
| № п/п | Наименование показателя | Формулы расчёта |
| 1 | Коэффициент осцилляции | 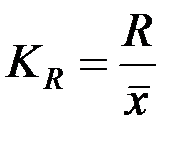
|
| 2 | Относительное линейное отклонение | 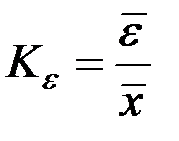
|
| 3 | Коэффициент вариации | 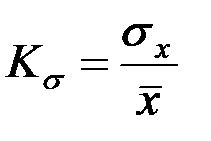
|
| 4 | Относительный показатель квартильной вариации | 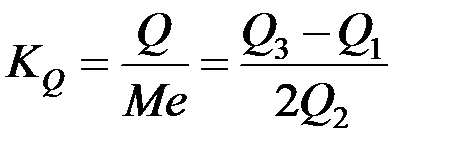
|
Пример 2.4. Вероятность того, что произвольный посетитель страховой компании заключит с ней какой–либо договор, равна 0,4. Определить математическое ожидание, дисперсию, среднее квадратическое отклонение, асимметрию, коэффициент вариации числа клиентов (из трёх посетителей), заключивших договор со страховой компанией.
Решение. Возможные значения СВ 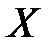 (число клиентов (из трёх посетителей), заключивших договор со страховой компанией): 0, 1, 2, 3.
(число клиентов (из трёх посетителей), заключивших договор со страховой компанией): 0, 1, 2, 3.
Используя формулу Бернулли (из теории вероятностей), вычислим вероятности различного числа клиентов (из трёх), заключивших договор со страховой компанией:
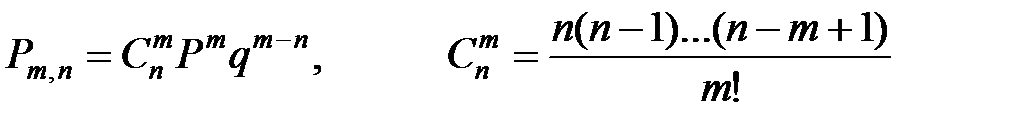 .
.
Ряд распределения СВ 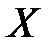 (число клиентов, заключивших договор со страховой компанией) имеет вид:
(число клиентов, заключивших договор со страховой компанией) имеет вид:
Значение СВ 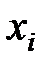
| 0 | 1 | 2 | 3 |
Вероятность 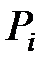
| 0,216 | 0,432 | 0,288 | 0,064 |
Вычислим числовые характеристики величины Х.
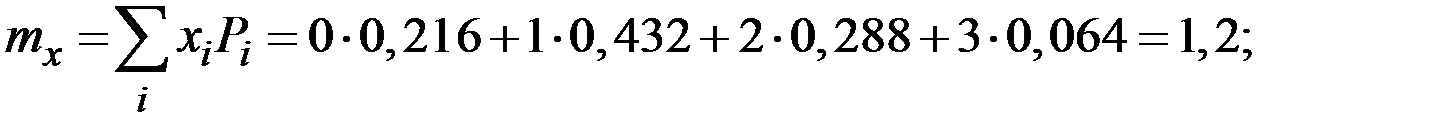
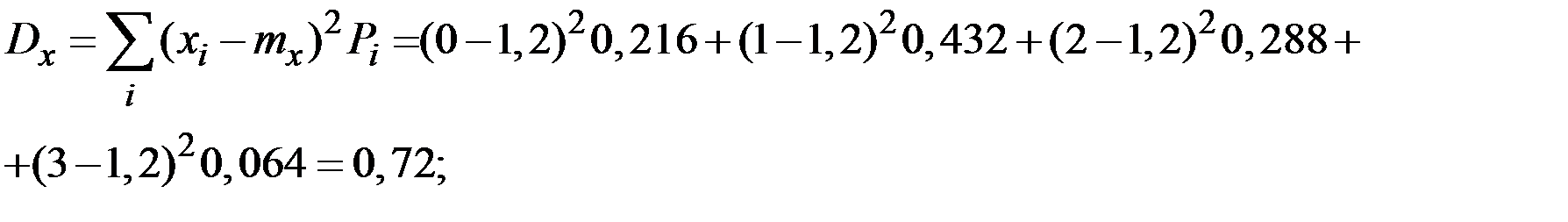
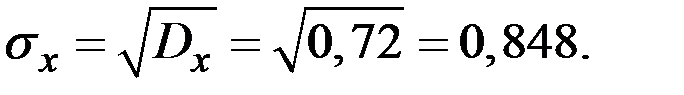
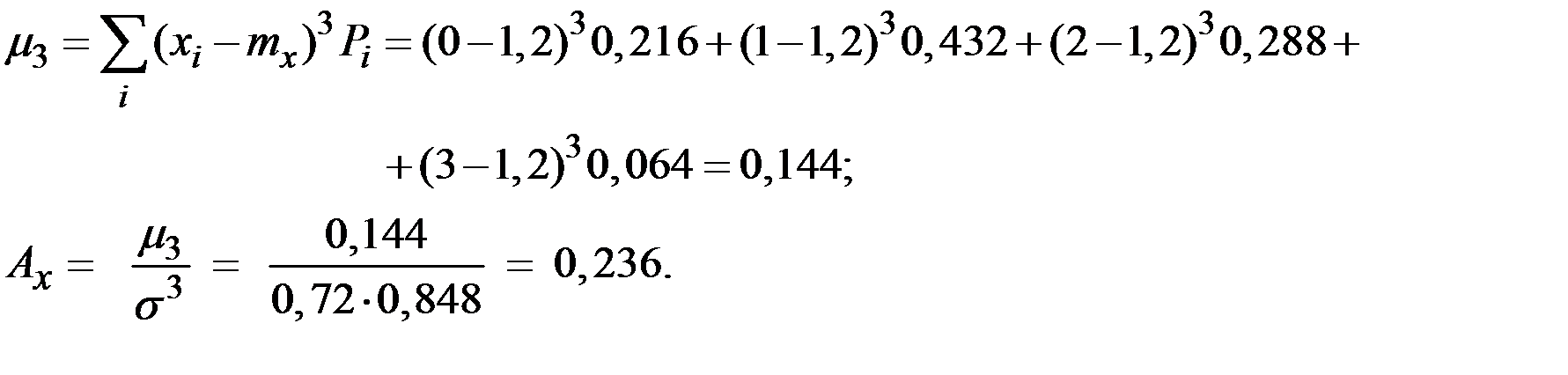
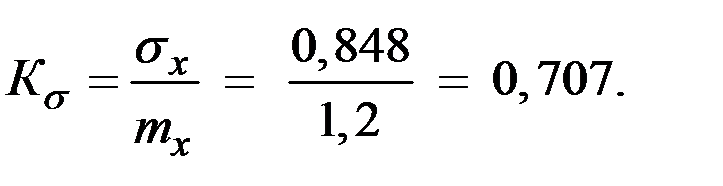
Пример 2.5. Непрерывная случайная величина Х подчинена закону распределения с плотностью.
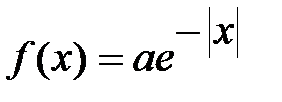
| 
| х |
Определить математическое ожидание, дисперсию, среднее квадратическоe отклонение, асимметрию, эксцесс величины Х.
Решение. Определим коэффициент а.
Для этого воспользуемся свойством плотности распределения
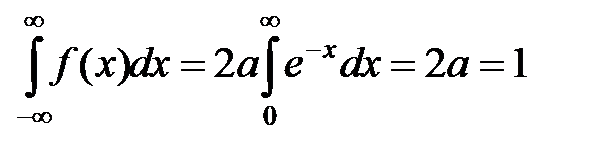 .
.
Отсюда а = 0,5.
Так как функция 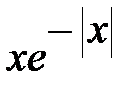 нечётная, то математическое ожидание величины Х равно нулю:
нечётная, то математическое ожидание величины Х равно нулю:
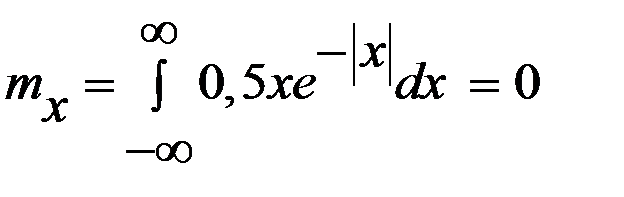 .
.
Дисперсия и среднее квадратичное отклонение, соответственно, равны:
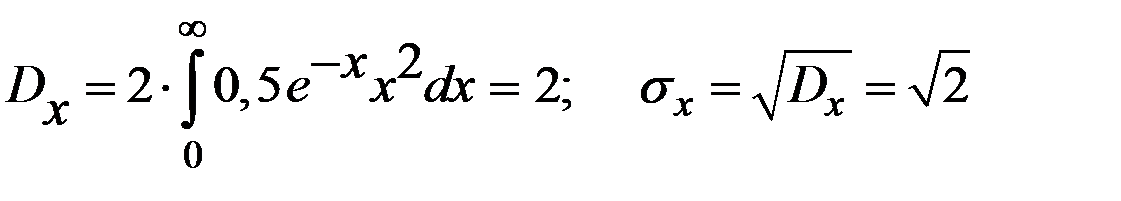 .
.
Так как распределение симметрично, то A х = 0.
Для вычисления эксцесса находим
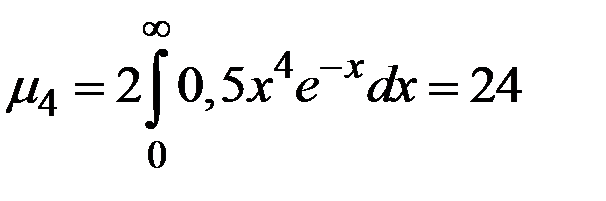 .
.
Отсюда
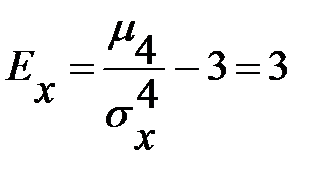 .
.
Пример 2.6. Доходы трёх банков от кредитов в отчётном году характеризуются следующими показателями:
| № банка | Средняя процентная ставка, r | Доход банка, тыс. руб., D |
| 1 | 20 | 600 |
| 2 | 30 | 480 |
| 3 | 35 | 350 |
| Итого | 1430 | |
Определить среднюю процентную ставку кредитов банков
Решение. Основой выбора формы средней является реальное содержание определяемого показателя:
Ставка, % = (доход банка / сумма кредита)×100%.
Средняя процентная ставка равна отношению доходов банков к сумме их кредитов. В данном примере отсутствуют прямые данные о кредитах. Но их суммы можно определить косвенным путём, разделив доход банка на процентную ставку.
Средняя процентная ставка трёх банков будет равна
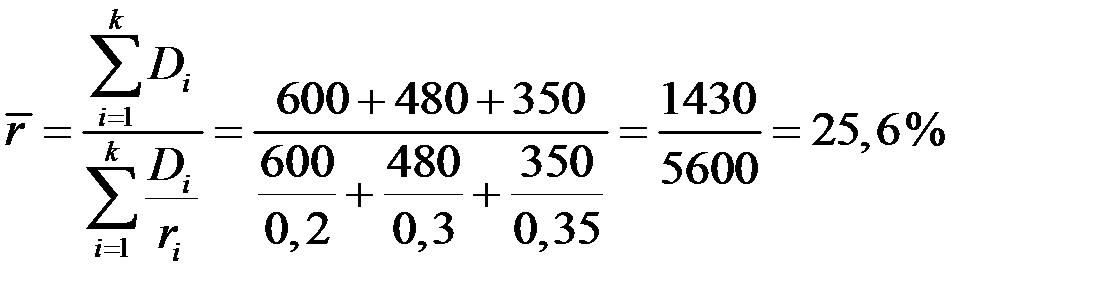 .
.
В этой средней гармонической взвешенной веса представляют собой произведения процентной ставки на сумму кредита.
Пример 2.7. Имеются следующие данные об остатках сырья и материалов на складе предприятия (в млн. рублей):
1) на 01.01.2016 г.: 400;
2) на 01.02.2016 г.: 455;
3) на 01.03.2016 г.: 465;
4) на 01.04.2016 г.: 465.
Определить среднемесячный остаток сырья и материалов на складе предприятия за первый квартал года.
Решение. По условию задачи имеем моментный ряд динамики с равными интервалами.
Поэтому среднемесячный остаток сырья и материалов на складе предприятия за первый квартал года по формуле простой средней хронологической:
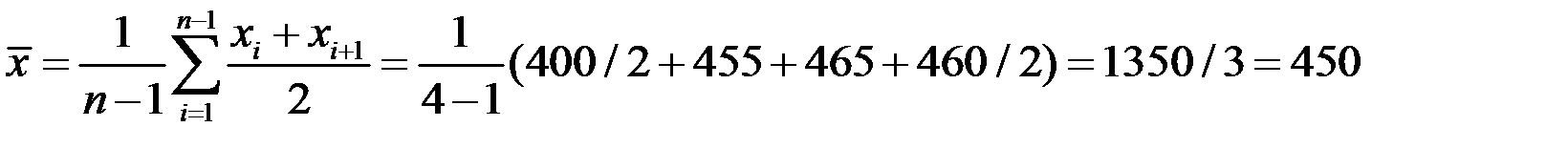 .
.
2.3. Основные законы распределения
2.3.1. Закон равномерной плотности
На практике встречаются непрерывные СВ, о которых заранее известно, что их возможные значения лежат в пределах некоторого определённого интервала.
Кроме того, известно, что в пределах этого интервала все значения СВ одинаково вероятны (точнее, обладают одной и той же плотностью вероятности). О таких СВ говорят, что они распределяются по закону равномерной плотности.
Пусть поезда метрополитена идут с интервалом 4 мин. Пассажир выходит на платформу в некоторый момент времени.
Время 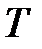 , в течение которого ему придётся ждать поезда, представляет собой величину, распределённую с равномерной плотностью на участке [0 – 4] минут.
, в течение которого ему придётся ждать поезда, представляет собой величину, распределённую с равномерной плотностью на участке [0 – 4] минут.
Плотность распределения для СВ Х, распределённой на участке 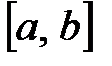 по закону равномерной плотности, выражается соотношением
по закону равномерной плотности, выражается соотношением