Расчёт медианы для интервального ряда производится по формуле
,
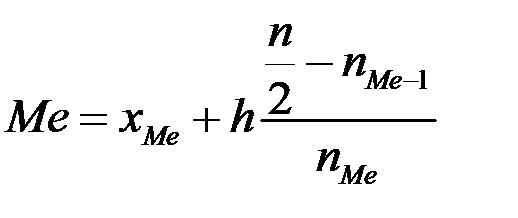где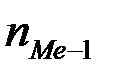 
– накопленная частота вариант, предшествующих медианному интервалу;
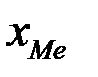– начало (нижняя граница) медианного интервала;
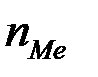– частота медианного интервала.
4. Дисперсией СВ называется математическое ожидание квадрата соответствующей центрированной величины (центрированной СВ называется разность между СВ Х и её математическим ожиданием):
.
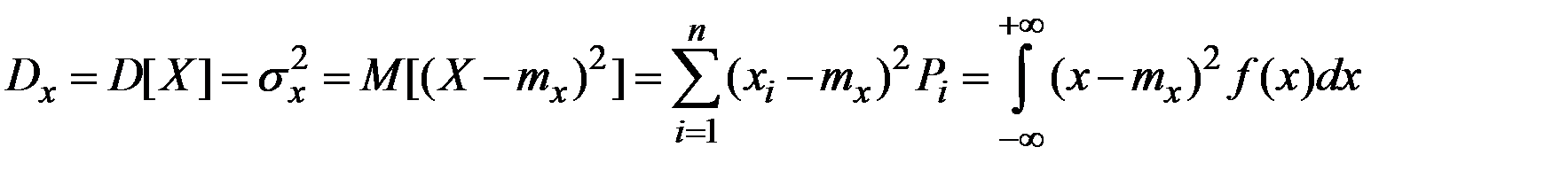5. Средним квадратическим отклонением СВ Х называется положительный корень из дисперсии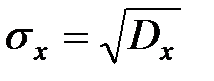 
.
Эта величина характеризует разброс значений СВ вокруг среднего значения (рис. 2.1).
|
|
|
|
|
|
|
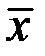
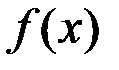
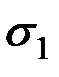
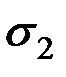
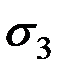
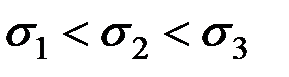
Рис. 2.1. Влияние среднего квадратического отклонения
на форму закона распределения
6. Коэффициент вариации СВ Х характеризует относительную изменчивость величины: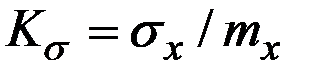 
.
7. Начальным моментом k – го порядка величины Х называется математическое ожидание k –й степени этой СВ.
Для дискретной и непрерывной СВ этот момент вычисляется, соответственно, по формулам:
.
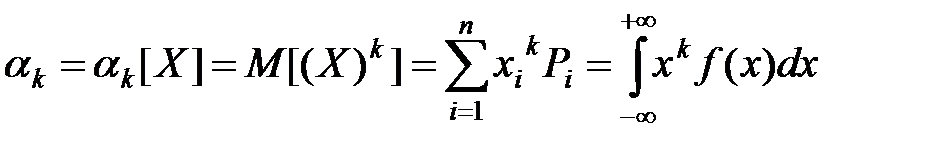8. Центральным моментом k–го порядка СВ Х называется математическое ожидание k–й степени центрированной СВ Х:
.
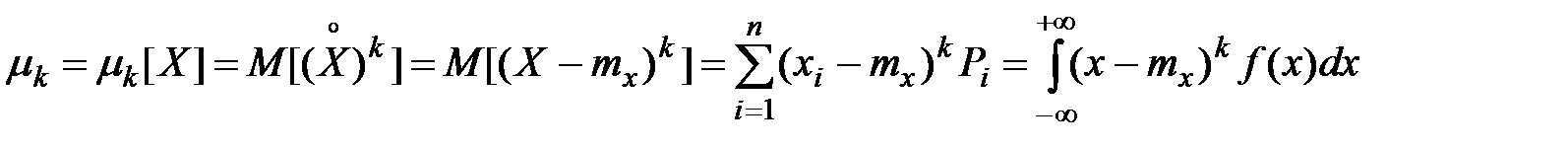Математическое ожидание СВ Х есть её первый начальный момент, а дисперсия – второй центральный.
Второй и третий центральные моменты выражаются через начальные моменты зависимостями:
.
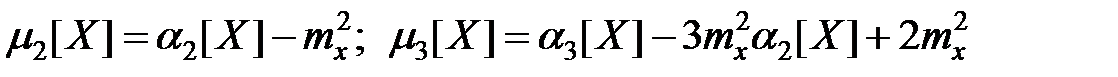9. Третий центральный момент служит для характеристики асимметрии (или скошенности) распределения.
Если распределение симметрично относительно математического ожидания (или в механической интерпретации, масса распределена симметрично относительно центра тяжести), то все моменты нечётного порядка (если они существуют) равны нулю.
Коэффициент асимметрии (или просто асимметрия) определяется зависимостью
.
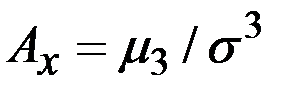10. Четвёртый центральный момент служит для характеристики "крутости", т.е. островершинности (или плосковершинности) закона распределения.
Это свойство распределения описываются с помощью так называемого эксцесса:
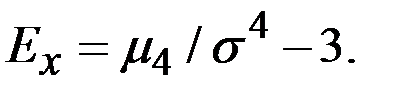
Для нормального распределения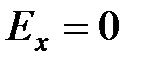 
.
Кривые, более островершинные по сравнению с нормальным законом, обладают положительным эксцессом; кривые более плосковершинные – отрицательным эксцессом.
|
|
|
|
|
|
|
|
|
|
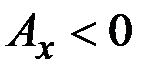
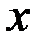
Рис. 2.2. Влияние асимметрии на форму закона распределения
Примечание. В статистике различают несколько видов средних величин: квадратическую, арифметическую, геометрическую, гармоническую, хронологическую. В зависимости от частоты повторения вариант средние исчисляются как простые, так и взвешенные (табл. 2.1).