Найти: коэффициент ; плотность распределения ; вероятность попадания СВ Х на участок от 0,25 до 0,5.
Решение. Так как функция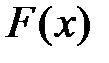 
непрерывна, то при 
.
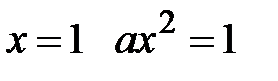Отсюда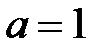 
. Плотность распределения СВ Х выражается формулой
.
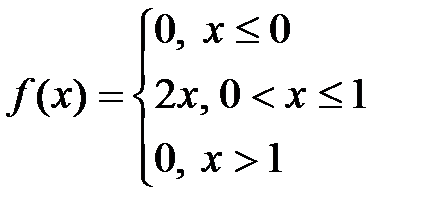Вероятность попадания величины Х на участок можно определить двумя способами:
.
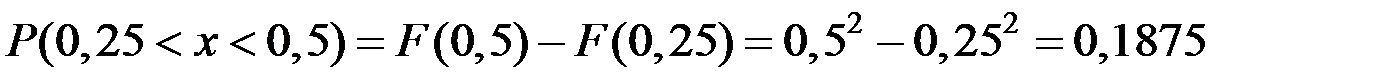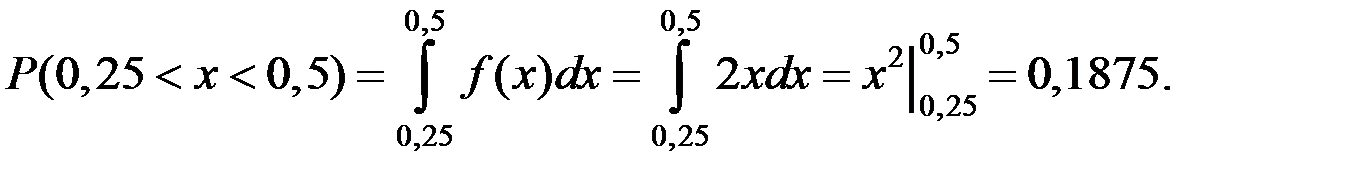
2.2. Числовые характеристики случайных величин
Каждая форма закона распределения (ряд распределения, функция распределения, плотность распределения) представляет собой некоторую функцию и полностью описывает СВ с вероятностной точки зрения.
Часто на практике требуется существенные сведения относительно СВ выразить в сжатой форме с помощью числовых (точечных) характеристик.
Основными числовыми характеристиками СВ являются следующие.
1. Математическое ожидание СВ Х это её среднее значение, которое вычисляется по формулам (соответственно, для дискретной и непрерывной СВ):
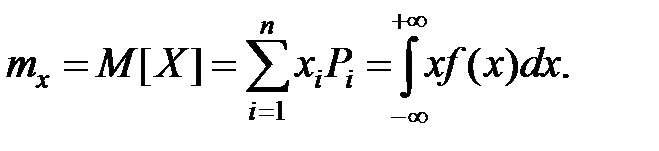
2. Мода (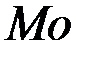 
) СВ – её наиболее вероятное значение для дискретной величины, а для непрерывной величины это то значение, в котором плотность распределения вероятностей максимальна.
Мода – варианта, встречающаяся в изучаемой совокупности чаще всего, т.е. варианта, которой соответствует наибольшая частота.
В интервальном ряду наибольшая частота указывает не на модальную варианту, а на содержащий моду интервал. Поэтому в модальном интервале необходимо определить модальную варианту.
При этом надо иметь в виду, что при расчётах будет получено не точное, а некоторое условное значение моды, так как неизвестен характер распределения частоты внутри модального интервала.
Вычисление моды производится по следующей формуле:
,
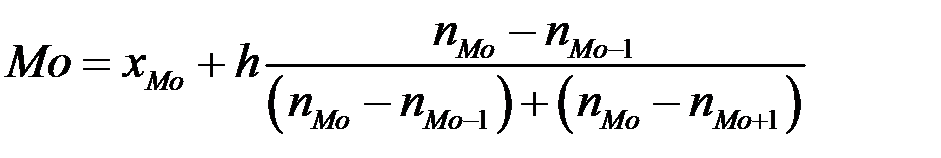где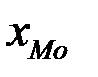 
– начало (нижняя граница) модального интервала;
h – величина интервала;
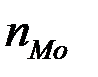– частота модального интервала;
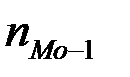– частота интервала, предшествующего модальному;
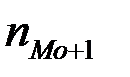– частота интервала, следующего за модальным.
3. Медиана случайной величины Х – такое её значение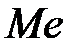 
, для которого
,
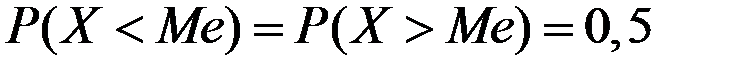т.е. одинаково вероятно, окажется ли СВ меньше или больше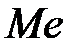 
.
Геометрически медиана – это абсцисса точки, в которой её площадь, ограниченная функцией плотности распределения, делится пополам.
Для определения медианы достаточно расположить в порядке возрастания или убывания все варианты. Серединная варианта и будет являться медианой.