Величина , определяемая равенством (где р задаётся), называется квантилем порядка р.
Квантиль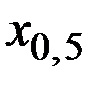 
порядка 0,5 называется медианой, квантили порядка 0,1; 0,2; ...; 0,9 называются децилями, квантили порядка 0,2; 0,4; 0,6; 0,8 называются квинтилями, а квантили порядка 0,25; 0,5; 0,75 называются квартилями.
Если функция распределения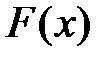 
везде непрерывна и имеет производную, то СВ называется непрерывной в узком смысле слова (или просто непрерывной).
Если функция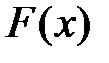 
на некоторых участках непрерывна, а в отдельных точках имеет разрывы, СВ называется смешанной.
Пример 2.1. Производятся 3 независимых выстрела по мишени с вероятностью попадания 0,4 в каждом. Получить функцию распределения СВ Х – числа попаданий в этих трёх выстрелах.
Решение.
Ряд распределения СВ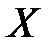 
(число попаданий) имеет вид:
Значение СВ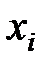 
| 0 | 1 | 2 | 3 |
Вероятность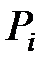 
| 0,216 | 0,432 | 0,288 | 0,064 |
Вероятности 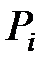вычислены по формуле Бернулли.
Тогда функция распределения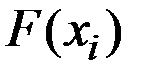 
(накапливая вероятности слева направо) будет иметь вид:
| Значение СВ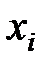
| (– ∞; 0) | [0; 1) | [1; 2) | [2; 3) | [3; ∞) |
|
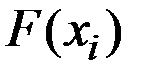
| 0 | 0,216 | 0,648 | 0,936 | 1,0 |
Пример 2.2. Статистика последних 3 лет свидетельствует о том, что месячная прибыль фирмы (тыс. долл.) является случайной величиной, которая изменялась в диапазоне (–10; 35) тыс. долларов и описывается следующей функцией распределения:
|
|
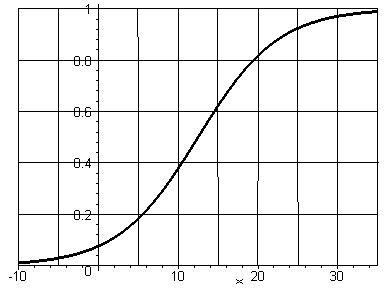
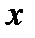
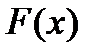
По виду графика оценить: 1) вероятность того, что прибыль произвольно взятого месяца будет заключена в пределах от 15 до 25 тыс. долл.; 2) вероятность того, что прибыль произвольно взятого месяца будет не менее 20 тыс. долл.; 3) вероятность того, что в произвольно взятом месяце будут убытки.
Решение.
Из графика видно, что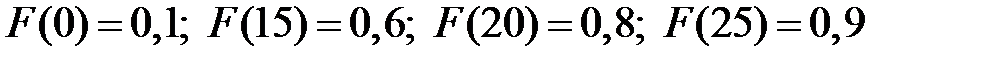 
.
Следовательно:
1) Вероятность того, что прибыль фирмы произвольно взятого месяца будет заключена в пределах от 15 до 25 тыс. долл., равна
.
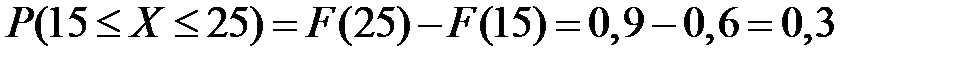2) Вероятность того, что прибыль произвольно взятого месяца будет не менее 20 тыс. долл., равна величине
.
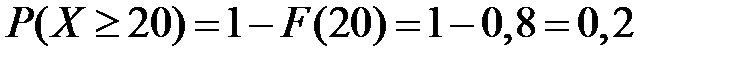3) Вероятность убытков в произвольно взятом месяце:
.
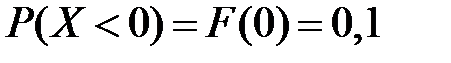3. Функция плотности распределения есть предел отношения вероятности попадания СВ в интервал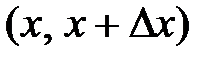 
к ширине этого интервала при её стремлении к нулю:
.
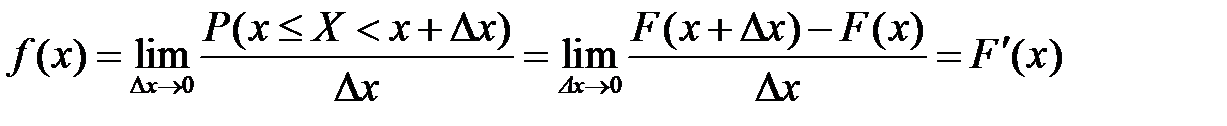Функцию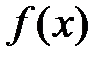 
называют также плотностью вероятностей, кривой плотности распределения. Плотность распределения существует только для непрерывных СВ и имеет следующие основные свойства:
;
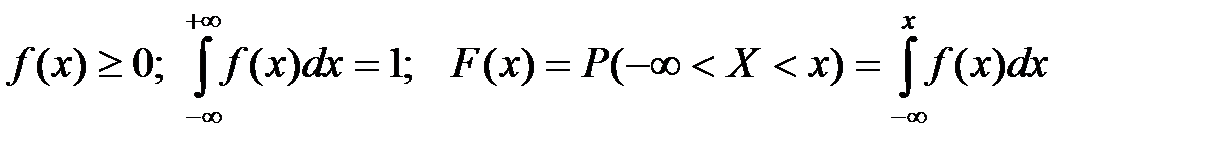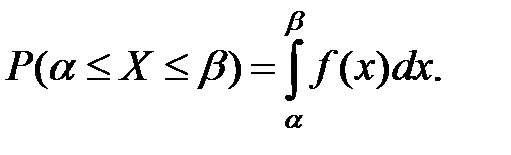
Пример 2.3. Функция распределения СВ Х задана выражением
.
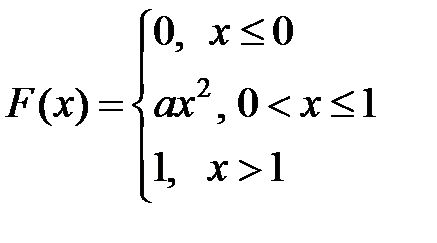