Контрольные задачи к разделу 1
1.1. В лотерее 10 билетов, из которых 4 выигрышных. Какова вероятность выиграть, имея 3 билета?
1.2. Телефонный номер состоит из 5 цифр. Найти вероятность того, что все цифры различны.
1.3. Какова вероятность вытащить два разноцветных шара, если в ящике 8 белых и 12 чёрных шаров?
1.4. У первого акционера имеется 9 акций вида А и 12 акций вида В. У второго, соответственно, 5 и 9. В результате операции купли/продажи 7 акций первого перешли ко второму держателю акций. Найти вероятность того, что случайно выбранная акция второго акционера окажется вида А.
1.5. Устройство состоит из 15 независимых блоков. Вероятность того, что неисправность может произойти в одном из первых трёх блоков составляет 0,6. При поиске появившейся неисправности обследованы первые два блока, но неисправность не обнаружена. Какова вероятность того, что неисправность будет обнаружена в третьем?
1.6. Определить вероятность того, что трёхзначный номер первой встретившейся автомашины не содержит одинаковых цифр и цифры шесть.
1.7. Из чисел 1, 2, 3, …, 15 одно за другим выбирают наугад два числа. Какова вероятность того, что разность между первым выбранным числом и вторым числом будет не меньше числа 3?
1.8. Стержень разламывается на две части в случайной точке, равномерно распределённой по всей длине стержня. Найти вероятность того, что меньший обломок имеет длину, не превосходящую одной трети длины стержня.
1.9. Для повышения надёжности прибора он дублируется тремя такими же приборами. Надёжность каждого прибора равна 0,6. Найти надёжность системы. Сколько надо взять приборов, чтобы надёжность системы стала 98%?
1.10. Из колоды в 32 карты берутся 4. Найти вероятность того, что среди них окажется хотя бы одна дама.
1.11. При переливании крови надо учитывать группы крови донора и больного. Человеку, имеющему четвертую группу крови, можно перелить кровь любой группы; человеку со второй или третьей группой крови можно перелить кровь либо той же группы, либо первой; человеку с первой группой крови можно перелить только кровь первой группы. Среди населения 30,7% имеют первую, 39,5% – вторую, 21,9% – третью и 7,9% – чётвертую группы крови. Найти вероятность того, что случайно взятому больному можно перелить кровь случайно взятого донора.
1.12. Какова вероятность того, что две произвольно взятые карты из колоды в 32 карты окажутся дамами?
1.13. Четыре поздравительные открытки случайно разложены по четырём конвертам с адресами. Найти вероятность того, что хотя бы одна открытка попала в свой конверт.
1.14. Брошены три игральные кости. Найти вероятность того, что сумма очков на выпавших гранях равна 4.
1.15. Из десяти билетов выигрышными являются два. Определить вероятность того, что среди взятых наудачу пяти билетов один выигрышный.
1.16. Устройство состоит из 5 элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включёнными окажутся неизношенные элементы.
1.17. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
1.18. Два игрока по очереди бросают игральную кость. Каждый по одному разу. Выигравшим считается тот, кто получит большее число очков. Найти вероятность выигрыша первого игрока.
1.19. В коробке 5 одинаковых изделий, 3 из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлечённых изделий окажется одно окрашенное изделие.
1.20. Среди 10 электрических лампочек три нестандартные. Найти вероятность того, что две одновременно лампочки окажутся нестандартными.
1.21. Пусть вероятность того, что покупателю необходима обувь 41–го размера, равна 0,2. Найти вероятность того, что из пяти первых покупателей обувь этого размера будет необходима одному.
1.22. Вероятность того, что монета диаметром d не пересечёт ни одну сторону квадратной сетки равна р. Определить размер сетки.
1.23. Два корабля должны подойти к одному и тому же причалу. Время прихода обоих кораблей независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из кораблей придётся ожидать освобождения причала, если время стоянки первого корабля составляет два часа, а второго – три часа.
1.24. На обслуживающее устройство в промежуток времени [0, 12] должны поступить 2 заявки. Если разность между моментами поступления заявок меньше 2, то вторая заявка теряется. Найти вероятность потери заявки.
1.25. Найти вероятность того, что сумма двух случайных чисел из отрезка [– 1, 2] больше единицы, а их произведение меньше единицы.
1.26. На пол, разграфлённый параллельными прямыми на полосы шириной а, бросается наугад игла длины l (l < a). Найти вероятность того, что игла пересечёт какую–нибудь прямую.
1.27. На плоскости отрезок длиной 10 см закреплён в одним концом и вращается вокруг точки закрепления так, что все направления отрезка равновероятны. Найти среднюю проекцию отрезка на заданную ось.
1.28. Вероятность того, что посетитель страховой компании заключит с ней какой–либо договор, равна 0,4. Сколько посетителей надо обслужить, чтобы с вероятностью не меньшей, чем 0,9, можно было утверждать, что будет заключён договор?
1.29. Стрельба заканчивается после второго попадания по мишени. Найти вероятность того, что при этом будет 4 промаха, если вероятность попадания при одном выстреле равна 0,35.
1.30. Производится залп из шести орудий по некоторому объекту. Вероятность попадания в объект из каждого орудия равна 0,6. Найти вероятность ликвидации объекта, если для этого необходимо не менее четырёх попаданий.
1.31. Вероятность хотя бы одного попадания стрелком в мишень при трёх выстрелах равна 0,875. Найти вероятность попадания при одном выстреле.
1.32. Сотрудники отдела маркетинга полагают, что в ближайшее время ожидается рост спроса на продукцию фирмы. Вероятность этого они оценивают в 80%. Консультационная фирма, занимающаяся прогнозом рыночной ситуации, подтвердила предположение о росте спроса. Положительные прогнозы консультационной фирмы сбываются с вероятностью 95%, а отрицательные – с вероятностью 99%. Какова вероятность того, что рост спроса действительно произойдёт?
1.33. 2 автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность 1–го автомата вдвое больше производительности 2–го. 1–й автомат производит в среднем 60% деталей отличного качества, а 2–й – 84% деталей отличного качества. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь изготовлена первым автоматом.
1.34. Два равносильных противника играют в шахматы. Что более вероятно: выиграть 2 партии из 4 или 3 партии из 6? Ничьи не рассматриваются.
1.35. Два баскетболиста делают по 3 броска мячом в корзину. Вероятности попадания мяча в корзину при каждом броске равны соответственно 0,6 и 0,7. Начти вероятность того, что у первого баскетболиста будет больше попаданий, чем у второго.
1.36. Известно, что в среднем 60% всего числа изготовляемых заводом телефонных аппаратов является продукцией первого сорта. Чему равна вероятность того, что в изготовленной партии окажется 6 аппаратов первого сорта, если партия содержит 10 аппаратов?
1.37. Рабочий обслуживает три станка. Каждый из станков может выходить из строя независимо друг от друга с вероятностями соответственно 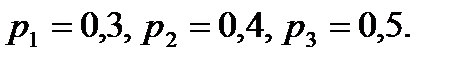 Стало известно, что вышел из строя один станок. Какова вероятность того, что это первый станок.
Стало известно, что вышел из строя один станок. Какова вероятность того, что это первый станок.
1.38. Прибор может собираться из высококачественных деталей и из деталей обычного качества. 40% приборов собирается из высококачественных деталей. Если прибор собран из высококачественных деталей, то его надёжность за время t равна 0,95, если из деталей обычного качества – его надёжность 0,7. Прибор испытывали в течение времени t и он отработал безотказно. Какова вероятность того, что он был собран из высококачественных деталей?
1.39. Найти вероятность того, что при случайной расстановке трёх ладей на шахматной доске они не будут угрожать друг другу.
1.40. Разрыв электрической цепи происходит в том случае, когда выходит из строя хотя бы одно из трёх последовательно соединённых элементов. Определить вероятность того, что не будет разрыва цепи, если элементы выходят из строя соответственно с вероятностями 0,3; 0,4 и 0,6.
1.41. Студент пришёл на экзамен, зная 20 из 25 вопросов программы. Экзаменатор задал студенту 3 вопроса. Найти вероятность того, что студент знает эти вопросы.
1.42. В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны: 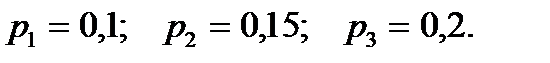 Найти вероятность того, что тока в цепи не будет.
Найти вероятность того, что тока в цепи не будет.
1.43. Оптовая база обслуживает 12 магазинов. От каждого из них заявка на товары на следующий день может поступить с вероятностью 0,3. Найти наивероятнейшее число заявок на следующий день.
1.44. Пассажир может обратиться за получением билета в одну из трёх касс. Вероятности обращения в кассы зависят от их местоположения и равны соответственно 0,2, 0,3 и 0,5. Вероятности того, что к моменту прихода пассажира имеющиеся в кассе билеты будут распроданы, равны: для первой кассы 0,2, для второй 0,3, для третьей 0,4. Пассажир направился за билетом в одну из касс и приобрёл билет. Какова вероятность того, что это была первая касса?
1.45. Имеется две партии деталей, причём известно, что в одной партии все детали удовлетворяют техническим условиям, а в другой партии 1/4 деталей недоброкачественные. Деталь, взятая из наудачу выбранной партии, оказалась доброкачественной. Определить вероятность того, что деталь взята из второй партии.
1.46. Вероятность возникновения опасной для прибора перегрузки в каждом опыте равна 0,4. Проводится испытание прибора в трёх независимых опытах. Вероятность отказа прибора при одной опасной перегрузке равна 0,2; при двух перегруз как равна 0,5; при трёх перегрузках равна 0,8. Определить вероятность отказа прибора в испытании.
1.47. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка M(a; b). Найти вероятность того, что корни уравнения x2 + ax + b = 0 будут действительными.
1.48. Станок–автомат штампует детали. Вероятность того, что за смену не будет выпущено ни одной нестандартной детали, равна 0,93. Найти вероят–ность того, что не будет выпущено ни одной нестандартной детали: а) за две смены; б) за три смены.
1.49. На факультете обучаются 650 студентов. Найти вероятность того, что ровно 4 студента имеют день рождения 1 апреля.
1.50. Вероятность наступления события в каждом опыте равна 0,2. Опыты производятся последовательно до наступления события. Найти вероятность того, что придётся производить четвёртый опыт.
1.51. В круг радиуса R вписан квадрат. Чему равна вероятность того, что поставленные наудачу внутри круга две точки окажутся внутри квадрата?
1.52. Имеются две партии изделий по 15 и 10 штук, причём в каждой партии есть одно бракованное изделие. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего выбирается изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии.
1.53. В ящике содержится 16 деталей завода № 1, 20 деталей завода № 2, 24 деталей завода № 3. Вероятность того, что детали завода № 1 отличного качества, равна 0,9; для деталей заводов № 2 и № 3 она соответственно равна 0,65 и 0,92. Найти вероятность того, что извлечённая наудачу деталь окажется отличного качества.
1.54. Вероятность того, что во время работы ЭВМ возникают сбои в процессоре, оперативной памяти и в остальных устройствах, относятся как 3:2:5. Вероятность обнаружения сбоя в процессоре, оперативной памяти и в остальных устройствах соответственно равны 0,84, 0,78 и 0,93. Найти вероятность того, что возникший в ЭВМ сбой будет обнаружен.
1.55. На сборку поступают детали с трёх автоматов. Первый выпускает 22%, второй – 30%, третий – 48% деталей данного типа. Первый автомат даёт 0,26% брака, второй – 0,13%, третий – 0,18%. Найти вероятность поступления на сборку бракованной детали.
1.56. Шар 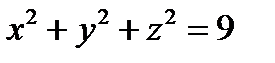 помещён внутри эллипсоида
помещён внутри эллипсоида 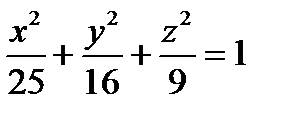 . Найти вероятность того, что брошенная наудачу внутрь эллипсоида точка окажется внутри шара.
. Найти вероятность того, что брошенная наудачу внутрь эллипсоида точка окажется внутри шара.
1.57. Пятнадцать экзаменационных билетов содержат по два вопроса, которые не повторяются. Студент может ответить только на 25 вопросов. Определить вероятность того, что экзамен будет сдан, если для этого достаточно ответить на два вопроса из одного билета или на один вопрос из первого билета и на дополнительный вопрос из другого билета.
1.58. Разрыв электрической цепи может произойти вследствие выхода из строя элемента А1 или двух элементов А2 и А3, которые выходят из строя независимо друг от друга соответственно с вероятностями 0,35, 0,24 и 0,12. Найти вероятность разрыва электрической цепи.
1.59. Найти вероятность того, что наудачу взятое двузначное число окажется кратным 2, либо 5, либо тому и другому одновременно.
1.60. Из последовательности чисел 1,2,3,…,10 наудачу выбираются два числа. Какова вероятность, что одно из них меньше 6, а другое больше 7?
1.61. Прибор может работать в 2 режимах: нормальном и в ненормальном. Нормальный режим наблюдается в 85% случаев, ненормальный – в 15% случаев. Вероятность выхода прибора из строя за время t в нормальном режиме равна 0,1, в ненормальном – 0,7. Найти вероятность выхода прибора из строя за время t.
1.62. Время ожидания связи с оператором банка подчиняется показательному закону распределения со средним значением 45 секунд. Найти вероятность того, что клиент будет ожидать связи с оператором более минуты.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ № 1
Задание № 1.1. Передача экономической информации от пункта А к пункту В может осуществляться по следующей схеме:
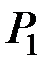
|
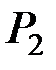
|
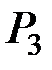
|
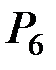
|
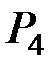
|
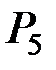
|
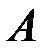
|
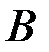
|
Здесь Рi – вероятности передачи информации без искажений в i–м блоке (i = 1,2,…,6) (табл. 1.1). Определить надёжность данной схемы, т.е. вероятность получения в пункте В достоверной (без искажений) информации.
Таблица 1.1
Варианты задания № 1.1
| № варианта | Значение вероятностей | |||||
| P1 | P2 | P3 | P4 | P5 | P6 | |
| 1 | 0,70 | 0,80 | 0,85 | 0,75 | 0,60 | 0,90 |
| 2 | 0,75 | 0,85 | 0,90 | 0,70 | 0,65 | 0,95 |
| 3 | 0,80 | 0,90 | 0,95 | 0,85 | 0,70 | 0,85 |
| 4 | 0,85 | 0,95 | 0,90 | 0,80 | 0,70 | 0,75 |
| 5 | 0,90 | 0,85 | 0,95 | 0,80 | 0,90 | 0,95 |
| 6 | 0,95 | 0,80 | 0,85 | 0,90 | 0,75 | 0,90 |
| 7 | 0,90 | 0,75 | 0,80 | 0,95 | 0,70 | 0,85 |
| 8 | 0,90 | 0,70 | 0,80 | 0,95 | 0,75 | 0,85 |
| 9 | 0,85 | 0,65 | 0,80 | 0,75 | 0,70 | 0,90 |
| 10 | 0,75 | 0,60 | 0,80 | 0,90 | 0,65 | 0,95 |
| 11 | 0,65 | 0,90 | 0,80 | 0,70 | 0,75 | 0,95 |
| 12 | 0,70 | 0,85 | 0,80 | 0,90 | 0,75 | 0,95 |
| 13 | 0,75 | 0,70 | 0,85 | 0,90 | 0,80 | 0,95 |
| 14 | 0,80 | 0,85 | 0,90 | 0,95 | 0,70 | 0,90 |
| 15 | 0,85 | 0,70 | 0,90 | 0,95 | 0,65 | 0,80 |
| 16 | 0,90 | 0,75 | 0,95 | 0,80 | 0,85 | 0,95 |
| 17 | 0,95 | 0,90 | 0,85 | 0,85 | 0,75 | 0,80 |
| 18 | 0,80 | 0,75 | 0,90 | 0,85 | 0,80 | 0,95 |
| 19 | 0,70 | 0,85 | 0,90 | 0,75 | 0,80 | 0,95 |
| 20 | 0,60 | 0,80 | 0,95 | 0,90 | 0,85 | 0,90 |
| 21 | 0,65 | 0,85 | 0,95 | 0,90 | 0,80 | 0,95 |
| 22 | 0,75 | 0,90 | 0,90 | 0,95 | 0,70 | 0,80 |
| 23 | 0,85 | 0,95 | 0,90 | 0,80 | 0,65 | 0,85 |
| 24 | 0,90 | 0,80 | 0,95 | 0,85 | 0,70 | 0,95 |
| 25 | 0,95 | 0,75 | 0,85 | 0,80 | 0,70 | 0,90 |
| 26 | 0,80 | 0,70 | 0,90 | 0,90 | 0,75 | 0,95 |
| 27 | 0,85 | 0,75 | 0,95 | 0,95 | 0,80 | 0,70 |
| 28 | 0,90 | 0,80 | 0,75 | 0,85 | 0,85 | 0,75 |
| 29 | 0,95 | 0,75 | 0,75 | 0,90 | 0,90 | 0,80 |
| 30 | 0,70 | 0,80 | 0,95 | 0,75 | 0,95 | 0,85 |
Задание № 1.2. На трёх станках при одинаковых и независимых условиях изготавливаются детали одного наименования. На первом станке изготавливается a %, на втором – b %, на третьем – c % всех деталей (табл. 1.2). Для каждой детали вероятность быть бездефектной равна Р1, если она изготовлена на первом станке, Р2 – если она изготовлена на втором станке, Р3 – если она изготовлена на третьем станке. Найти вероятность того, что наугад взятая деталь не окажется дефектной.
Таблица 1.2
Варианты исходных данных задания № 1.2
| № варианта | Значения параметров | |||||
| a | b | c | P1 | P2 | P3 | |
| 1 | 10 | 30 | 60 | 0,90 | 0,80 | 0,75 |
| 2 | 20 | 15 | 65 | 0,85 | 0,90 | 0,70 |
| 3 | 50 | 40 | 10 | 0,80 | 0,95 | 0,85 |
| 4 | 65 | 15 | 20 | 0,75 | 0,85 | 0,90 |
| 5 | 20 | 30 | 50 | 0,60 | 0,70 | 0,85 |
| 6 | 30 | 25 | 45 | 0,40 | 0,90 | 0,95 |
| 7 | 10 | 80 | 10 | 0,90 | 0,80 | 0,75 |
| 8 | 5 | 35 | 60 | 0,65 | 0,85 | 0,80 |
| 9 | 30 | 55 | 15 | 0,95 | 0,90 | 0,80 |
| 10 | 15 | 65 | 20 | 0,75 | 0,80 | 0,90 |
| 11 | 30 | 45 | 25 | 0,85 | 0,75 | 0,90 |
| 12 | 30 | 10 | 60 | 0,70 | 0,80 | 0,75 |
| 13 | 15 | 25 | 60 | 0,90 | 0,85 | 0,65 |
| 14 | 55 | 25 | 20 | 0,75 | 0,95 | 0,70 |
| 15 | 45 | 25 | 30 | 0,80 | 0,65 | 0,95 |
| 16 | 45 | 30 | 25 | 0,60 | 0,90 | 0,95 |
| 17 | 40 | 50 | 10 | 0,90 | 0,80 | 0,95 |
| 18 | 55 | 10 | 35 | 0,85 | 0,95 | 0,75 |
| 19 | 40 | 15 | 45 | 0,70 | 0,85 | 0,90 |
| 20 | 25 | 15 | 60 | 0,85 | 0,95 | 0,80 |
| 21 | 10 | 40 | 50 | 0,85 | 0,75 | 0,90 |
| 22 | 20 | 25 | 55 | 0,90 | 0,80 | 0,65 |
| 23 | 50 | 10 | 40 | 0,75 | 0,80 | 0,95 |
| 24 | 35 | 40 | 25 | 0,70 | 0,85 | 0,90 |
| 25 | 20 | 70 | 10 | 0,90 | 0,65 | 0,70 |
| 26 | 35 | 70 | 25 | 0,85 | 0,70 | 0,65 |
| 27 | 50 | 20 | 30 | 0,95 | 0,75 | 0,70 |
| 28 | 10 | 40 | 55 | 0,70 | 0,80 | 0,80 |
| 29 | 20 | 35 | 60 | 0,75 | 0,85 | 0,85 |
| 30 | 35 | 30 | 10 | 0,80 | 0,90 | 0,95 |
Задание № 1.3. На склад поступила партия из N деталей, среди которых M дефектных. Из партии для контроля выбираются случайным образом K изделий (табл. 1.3). Если среди контрольных окажется более L дефектных, то вся партия бракуется. Найти вероятность того, что партия будет забракована.
Задание № 1.4. В одном ящике упаковано N1 деталей, из них M1 с дефектами; в другом ящике упаковано N2 деталей, из них M2 с дефектами (табл. 1.3). Контролёр случайным образом открыл один из этих ящиков, взял деталь на экспертизу. Деталь оказалась с дефектом. Какова вероятность того, что и вторая деталь из того же ящика окажется с дефектом?
Таблица 1.3
Варианты исходных данных заданий № 1.3, 1.4
| № варианта | Значения величин | |||||||
| N | M | K | L | N1 | M1 | N2 | M2 | |
| 1 | 50 | 4 | 5 | 2 | 10 | 2 | 12 | 4 |
| 2 | 40 | 4 | 4 | 1 | 8 | 3 | 9 | 6 |
| 3 | 30 | 3 | 4 | 1 | 100 | 14 | 112 | 20 |
| 4 | 20 | 3 | 3 | 1 | 20 | 5 | 16 | 6 |
| 5 | 10 | 3 | 3 | 1 | 40 | 10 | 20 | 8 |
| 6 | 30 | 4 | 5 | 2 | 12 | 3 | 11 | 5 |
| 7 | 40 | 6 | 4 | 1 | 15 | 5 | 10 | 4 |
| 8 | 50 | 5 | 5 | 2 | 20 | 5 | 14 | 4 |
| 9 | 60 | 8 | 6 | 3 | 25 | 10 | 20 | 12 |
| 10 | 70 | 10 | 7 | 4 | 20 | 6 | 18 | 7 |
| 11 | 80 | 10 | 6 | 2 | 30 | 6 | 40 | 10 |
| 12 | 80 | 8 | 5 | 2 | 20 | 3 | 22 | 2 |
| 13 | 70 | 5 | 4 | 2 | 10 | 3 | 12 | 5 |
| 14 | 30 | 4 | 3 | 1 | 30 | 5 | 35 | 7 |
| 15 | 50 | 5 | 4 | 2 | 50 | 5 | 60 | 10 |
| 16 | 40 | 6 | 4 | 1 | 70 | 7 | 35 | 6 |
| 17 | 30 | 7 | 5 | 3 | 40 | 8 | 50 | 4 |
| 18 | 30 | 8 | 5 | 2 | 26 | 4 | 28 | 10 |
| 19 | 60 | 9 | 6 | 2 | 16 | 4 | 20 | 8 |
| 20 | 70 | 10 | 6 | 3 | 40 | 8 | 30 | 10 |
| 21 | 50 | 11 | 7 | 2 | 10 | 7 | 15 | 6 |
| 22 | 40 | 12 | 7 | 3 | 100 | 15 | 80 | 20 |
| 23 | 40 | 10 | 4 | 2 | 150 | 40 | 160 | 30 |
| 24 | 30 | 6 | 5 | 3 | 250 | 50 | 400 | 40 |
| 25 | 30 | 8 | 6 | 3 | 80 | 10 | 70 | 12 |
| 26 | 60 | 5 | 4 | 1 | 10 | 3 | 10 | 6 |
| 27 | 70 | 4 | 5 | 3 | 70 | 5 | 15 | 4 |
| 28 | 80 | 3 | 5 | 3 | 50 | 6 | 80 | 10 |
| 29 | 40 | 5 | 7 | 2 | 40 | 8 | 35 | 7 |
| 30 | 50 | 7 | 6 | 1 | 50 | 7 | 50 | 5 |
2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.1. Описание случайных величин
Случайной величиной (СВ) называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно.
Дискретной (прерывной) называется СВ, принимающая отдельные друг от друга значения, которые можно пронумеровать. Например: число появлений герба при трёх бросаниях монеты (возможные значения 0, 1, 2, 3), частота появления герба в том же опыте (возможные значения 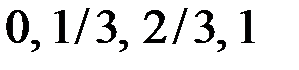 ), количество студентов на занятиях, количество сбоев устройства за некоторый интервал времени и т.п.
), количество студентов на занятиях, количество сбоев устройства за некоторый интервал времени и т.п.
Возможные значения непрерывных СВ не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток. Например: время безотказной работы прибора, расстояние от точки попадания до центра мишени, рост человека, температура воздуха, напряжение в сети, прибыль фирмы и т.п.
СВ полностью описывается своим законом распределения.
Законом распределения СВ называется всякое соотношение (функция), устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.
Закон распределения может иметь три формы.
1. Рядом распределения дискретной СВ Х называется таблица, где перечислены возможные (различные) значения этой СВ 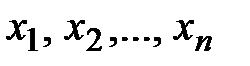 с соответствующими им вероятностями
с соответствующими им вероятностями 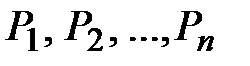 .
.
При этом 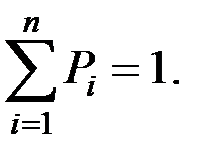
Графическое изображение ряда распределения называется многоугольником (полигоном) распределения.
2. Функцией распределения СВ Х называется функция 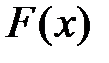 , выражающая вероятность того, что Х примет значение, меньшее, чем какое–то заданное конкретное значение
, выражающая вероятность того, что Х примет значение, меньшее, чем какое–то заданное конкретное значение 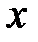 :
:
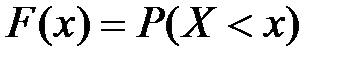 .
.
Функцию распределения 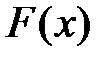 иногда называют также интегральной функцией распределения или интегральным законом распределения.
иногда называют также интегральной функцией распределения или интегральным законом распределения.
Функция распределения – универсальная характеристика СВ.
Функция распределения существует для всех СВ: как дискретных, так и непрерывных.
Свойства функции распределения.
1) Функция 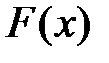 есть неубывающая функция своего аргумента, т.е. при
есть неубывающая функция своего аргумента, т.е. при 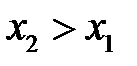 имеет место соотношение
имеет место соотношение 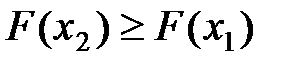 .
.
2) 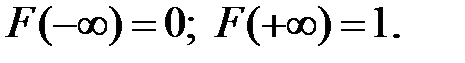
3) Для дискретных СВ 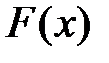 есть разрывная ступенчатая функция, непрерывная cлева.
есть разрывная ступенчатая функция, непрерывная cлева.
4) Выразим вероятность попадания СВ на заданный участок через функцию распределения F(x).
Для этого рассмотрим три события
| A – событие, состоящее в том, что X < b ; B – событие, состоящее в том, что X < a ; C – событие, состоящее в том, что a Ј X < b | 
|
Учитывая, что A = B + C, по теореме сложения вероятностей имеем:
P(X <b) = P(X <a) + P(a Ј X < b)
или
F(b) = F(a) + P(a Ј X < b).
Отсюда получим:
P(a Ј X < b) = F(b) – F(a).
Т.е. вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке.
Если случайная величина X непрерывна, то P(X = a) = 0 и можем записать
P(a < X < b) = P(a Ј X < b) = P(a < X Ј b) = P(a Ј X Ј b) = F(b) – F(a).








